小學數學結構化教學的“四化”策略

黃敏珊

小學數學如何進行結構化教學？在筆者課題組“基于學生學習路徑分析的結構化教學實踐研究”的實踐研究中，提煉出“把準知識的體系化、核心目標具體化、學生思維層級化、課堂教學結構化”的教學策略。下面，以四年級“平均數”教學為例，具體談談如何從這“四化”進行結構化教學。

一、知識體系化

結構化教學，首先要有大觀念的宏觀視野，對教學內容的知識體系進行整體分析、單元分析，理清知識的脈絡，精準分析知識的前后聯系，把準本節課的核心要素。這樣可以幫助學生將個別的知識與技能與更大的認知架構相聯結，有利于學生洞察知識的本質，遷移運用所學的知識。

筆者將幾個版本“平均數”這一內容的教材進行對比，各版本都是利用幾何直觀，并鼓勵學生在具體的情境中收集、整理和表達數據，從而讓他們理解平均數的統計概念和計算方法。

二、目標具體化

結構化教學使得核心素養在課堂中獲得真正的發掘與涵養。將核心目標具體化，是建立在知識的體系構建和符合學生的認知規律的基礎之上。結合學生的實際情況，為有效推進教學，將核心目標理解平均數的意義進行了細致的劃分，具體而言，將其分為五個具體的表現：1.不知道平均數；2.會移多補少或算術法求平均數；3.知道平均數能表示該組數據的整體水平；4.知道平均數的虛擬性、區間性、敏感性；5.知道平均數的代表性，能進行推斷或預測。其中，第2說明學生的理解達到了算法水平，3和4說明學生理解達到了概念水平，5說明學生理解達到了統計水平。

三、思維層級化

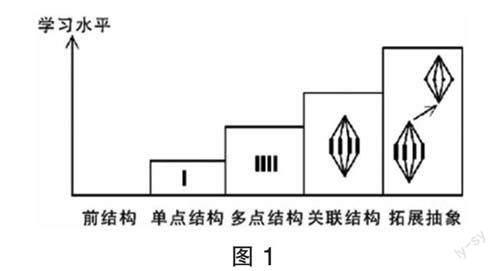
學生的思維發展不盡相同，自始至終都伴隨著階段、層級和連貫性的變化。依據學生在解答特定問題時展示的認知進程，SOLO分類理論將其細分為五個層次（如下頁圖1）。通過運用SOLO理論，將學生的思維過程可視化，并對其進行層級分析，以此為基礎設計有針對性的教學活動，使學生的思維能夠不斷進階并向更高級別發展，是結構化教學的有效手段。

基于學生生活經驗，調查的學生中只有3人不知道平均數，大多數學生都對平均數有所了解，只有約6.25%的學生處于前結構結構水平。據統計，前測中有70.83%的學生能熟練掌握平均數的求解方法，有相當數量的學生仍處于單點結構水平上。雖然有一半以上的學生意識到平均分和平均數之間的差異，但16.67%的學生能恰當地運用平均數來表達數據的整體水平，并且還不能清晰地解釋說明平均數的意義，這些學生處于多點結構水平。只有6.25%的學生知道平均值的某些屬性。通過分析可以得知，多數學生的認知水平僅達到算法層面，而僅有少數學生的理解水平達到概念層面。

四、課堂結構化

落實結構化教學，還需構建清晰完整的教學結構。“五構”教學是教師精心設計大任務，由散構、建構、解構、固構、延構組成。在整體把握教材知識體系，將核心目標具體化，并精準分析學生的思維層級的基礎上，運用“五構”教學模式。

1.散構：激活經驗，產生需求

散構意在激活、調動學生學習的相關經驗，產生頭腦風暴，充分調動學生的思維。課始創設了“學校踢毽子比賽，每個班要選一個代表參賽，怎么選參賽選手？”的情境，激發學生的探究欲望。讓學生看著視頻記錄數據，學會用數學的眼光去觀察，親歷數據收集、整理的過程。“你認為該哪個數據代表小亮踢毽子的水平？”一語激起學生的思維，學生在討論過程中發現之前的知識已不能解決這個問題，用“平均數”表示的需求呼之欲出。

2.建構：引導發現，初步感悟

建構是理解所學新知，將新知建立表象，初步建立結構。劉加霞教授認為學生對平均數的理解第一層次是算術平均數，也就是首先要明白平均數是怎樣來的，會計算平均數。基于前面學生提出用18來代表他的水平，圍繞“18哪里來的？”這一問題學生思考探究，在交流后得出用“移多補少”和“先合后分”兩種方法得出平均數18。

3.解構：探索意義，理解內涵

解構即是解開結構，是為更好的理解新知，將新知融入原有結構之中。學生在掌握平均數的算法基礎上，要深入理解平均數的意義，還要需要在多組數據中去進一步感悟、對比、分析和體會。于是，筆者設計了如下三個層層遞進的環節，兩次變式，多次對比，讓學生逐步深入感悟、體驗，深化理解平均數的內涵，培養學生的數據意識。

首先，理解平均數的公平性。“小明和小亮踢毽子的成績對比，他們誰的水平更高呢？”這里學生會用總數和平均數進行比較，通過交流說理，得出當踢的次數相同時，用總數與平均數都能公平選出。

其次，理解平均數的代表性。出示三個學生踢毽子成績，提出“現在怎么選才公平？”“為什么用平均數比較公平？”圍繞這些問題，通過條形統計圖直觀對比，發現平均數所處位置，在最小值和最大值之間，再將平均數和組內其他數據比較，理解不同數據的意義。

第三，理解平均數的隨機性。在學生理解的基礎上繼續變換組中數據，增加一個數據，改變一個數據，利用直觀的條形圖，觀察平均數的位置變化，計算出平均數，感悟平均數的隨機性以及區間性。

4.固構：再次驗證，靈活應用

固構即是變式訓練，達到靈活應用。結合本節課的教學內容，設置了課堂練習。基礎練習：求某個小組6人的平均身高，鞏固求平均數的方法；過關練習：水池平均水深110cm，身高140cm有沒有溺水危險？通過情境判斷體會平均數的虛擬性、區間性。拓展練習：想知道班級各小組人均閱讀量的高低，可以怎么做？讓學生學會收集整理數據，并能用平均數進行分析幫助決策，解決生活中的簡單問題，提升學生的應用意識。通過不斷深入練習，逐步加深學生對平均數統計意義的內化理解，并培養他們在實際運用中的靈活性。

5.延構：對比啟思，深度理解

延構是將新知融入原認知結構，在新舊知識間建立聯系。學生特別容易將平均分與平均數兩個概念混淆不清，因此，理解平均數和平均分的相同點和不同點，有助于幫助學生將新舊知識建立聯系。讓學生在質疑爭辯中溝通兩者的聯系與區別：都是除法計算，但是平均分得到的是實際分得的數，而平均數卻是一個虛擬的數，代表的是一組數據的整體的水平。

綜上，運用“四化”策略的結構化教學不僅將數學核心素養落地貫穿始終，而且更加有效構建貼近學生、整體關聯、層次清晰、目標具體、邏輯嚴密的課堂，以此激活學生思維，增強學情體驗，進一步完善認知體系，促進深度學習，培育核心素養。

【注：本文系廣東省教育研究院2022年中小學數學教學研究專項課題“基于學生學習路徑分析的小學數學結構化教學實踐研究”（GDJY-2022-M-b29）的階段性研究成果】

責任編輯 韋英哲