挖掘課本資源,促進(jìn)高階思維能力發(fā)展
周紅永
? 江蘇徐州睢寧縣桃園中學(xué)
新課標(biāo)要求培養(yǎng)學(xué)生的創(chuàng)新精神與獨(dú)立自主的學(xué)習(xí)能力.課標(biāo)的落實(shí),要以課本為載體.教學(xué)中以課本例題或練習(xí)題為基礎(chǔ),細(xì)解讀,精加工,再重組,實(shí)現(xiàn)知識的有機(jī)統(tǒng)一,讓學(xué)生在結(jié)構(gòu)知識的引領(lǐng)下喚醒舊知識,引發(fā)新知識,從而促進(jìn)學(xué)生的數(shù)學(xué)高階思維能力發(fā)展.高階思維是指發(fā)生在較高認(rèn)知水平層次上的心智活動或認(rèn)知能力,在認(rèn)知過程分類中表現(xiàn)為分析、評價(jià)和創(chuàng)造.其中,分析指的是一種系統(tǒng)性思維,要求從整體上把握各部分的聯(lián)系,從而理解事物的本質(zhì).因此,教學(xué)中要通過發(fā)現(xiàn)問題,并找出問題的癥結(jié),不斷發(fā)展學(xué)生的高階思維能力.筆者把平時(shí)的做法做了如下反思.
1 溯本求源,提高學(xué)生高階思維能力
在八年級剛開始,學(xué)生對復(fù)雜圖形的證明問題打不開思路,看圖的視野僅局限于題目本意,缺乏聯(lián)想思維,所以解題時(shí)總是無從下手,有時(shí)即使有切入點(diǎn)也顯得沒有條理.聽了楊裕前教授的講座《溯本求源 正本清源》,猶如醍醐灌頂.圖形的識別要用運(yùn)動的眼光去看,平移、旋轉(zhuǎn)與翻折是圖形變換的基礎(chǔ),所以教學(xué)中要學(xué)會溯本求源,尋找基本的圖形運(yùn)動,建立模型,利用轉(zhuǎn)化思想找到思考的突破口,開闊學(xué)生解題的視野,幫助學(xué)生能站在更高的出發(fā)點(diǎn)去解題.
問題1(課本原題改編)如圖1,若點(diǎn)A在線段BC上,△ABD,△AEC都是等邊三角形,AD與BE相交于點(diǎn)G,AE與CD相交于點(diǎn)F.你能從條件出發(fā),運(yùn)用聯(lián)想,通過獨(dú)立思考把能直接或間接知道的量盡可能地在找出來嗎?

圖1
在學(xué)生解答問題1之前,先幫助學(xué)生梳理幾個(gè)有價(jià)值的思考方向,引導(dǎo)如下:
(1)圖2中有哪些相等的線段、相等的角?
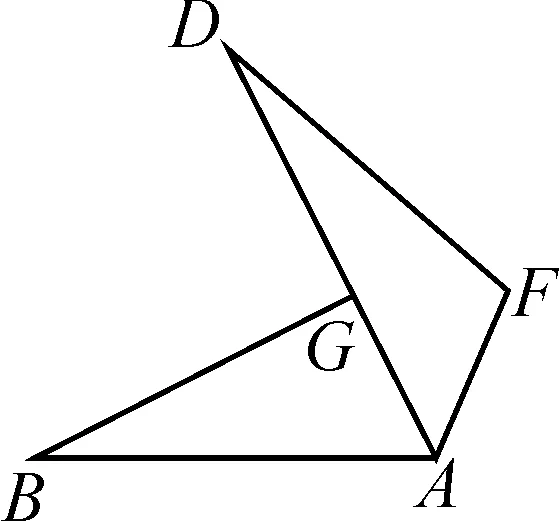
圖2
(2)你還能間接推導(dǎo)出哪些角相等?
(3)誰看出圖1中還有我們已經(jīng)學(xué)習(xí)過的什么圖形?(學(xué)生可以很快看出△BAE≌△DAC,如圖3.) △BAE是怎樣變化得到△DAC的?由全等三角形的性質(zhì)你還可以得到什么?
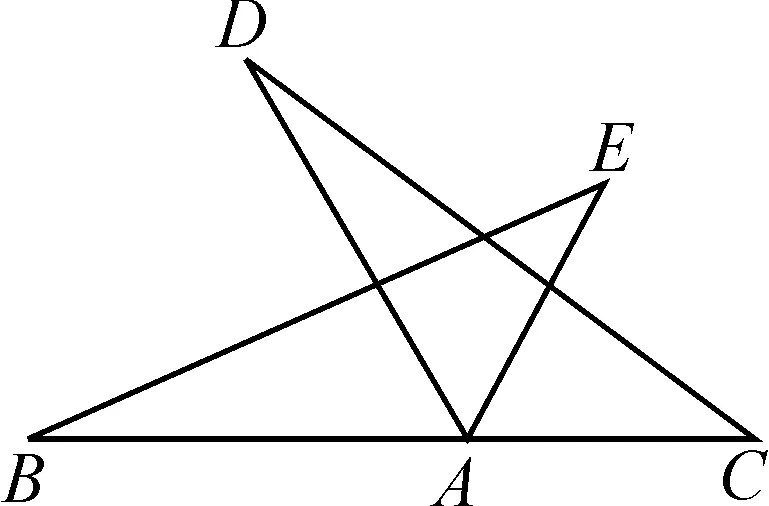
圖3
(4)還有沒有其他全等的三角形?
從最基本的線段和角入手,分解讀圖的難度.由∠BAE=∠DAC聯(lián)想到角的和差關(guān)系,從而自然聯(lián)想到最基本圖形運(yùn)動產(chǎn)生的全等模型.教材的例題、習(xí)題不斷地強(qiáng)化從運(yùn)動的角度認(rèn)識全等,學(xué)生可以聯(lián)想到△ABG≌△ADF,題目便很容易解決.
2 挖掘教材中可替代圖形,通過遷移變化提高學(xué)生高階思維能力
以問題為切入點(diǎn),回歸課本,挖掘教材中可替代圖形,鍛煉學(xué)生轉(zhuǎn)化思想,培養(yǎng)發(fā)散思維和創(chuàng)新能力.利用變式訓(xùn)練來促進(jìn)學(xué)生的思考,從而提高學(xué)生高階思維的能力.
問題2(課本原題)如圖4,在△ABC中,分別以AB,AC為邊,向△ABC外作正三角形,BE,CD相交于點(diǎn)O.

圖4
(1)試說明△ABE≌△ADC;
(2)探究:∠BOC=______.
變式1如圖5,圖6,在△ABC中,分別以AB,AC為邊,向△ABC外作正四邊形、正五邊形,BE,CD相交于點(diǎn)O.試說明:①△ABE≌△ADC.②圖5中,∠BOC=______;如圖6,∠BOC=______.

圖5
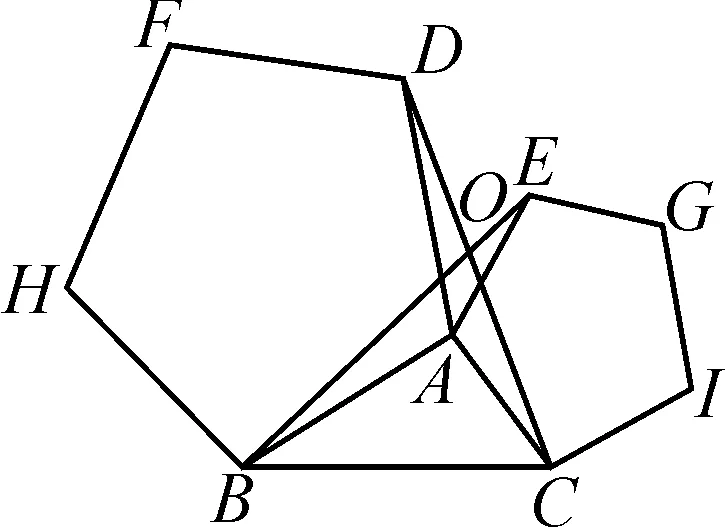
圖6
如圖7,如果AB,AD是以AB為邊向△ABC外所作正n邊形的一組鄰邊;AC,AE是以AC為邊向△ABC外所作正n邊形的一組鄰邊;BE,CD的延長相交于點(diǎn)O.試猜想:∠BOC=______(用含n的式子表示).

圖7
這樣基于課本原題的變式設(shè)計(jì),使學(xué)生在變化中找尋不變性,靈活地運(yùn)用知識,養(yǎng)成樂于思考的習(xí)慣,使思維的發(fā)展更進(jìn)一步.
變式2等邊三角形可以用等腰直角三角形或正方形來代替.
例1如圖8,△ABD,△AEC都是等邊三角形,求證:BE=DC.

圖8
(由已知易證△ABE≌△ADC,得BE=DC.)
變式練習(xí):(1)如圖9,若△ABD,△AEC都是等腰直角三角形,∠ADB=∠AEC=90°,那么BE=DC嗎?
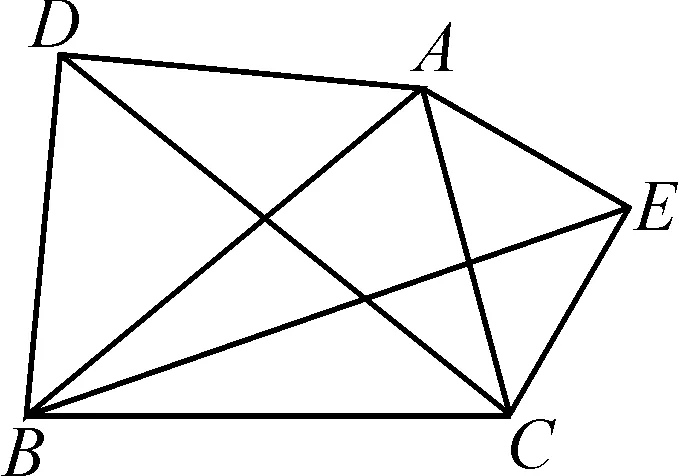
圖9
(2)如圖10,若四邊形ABFD、四邊形ACGE都是正方形,那么BE=DC還成立嗎?求證BE⊥DC.
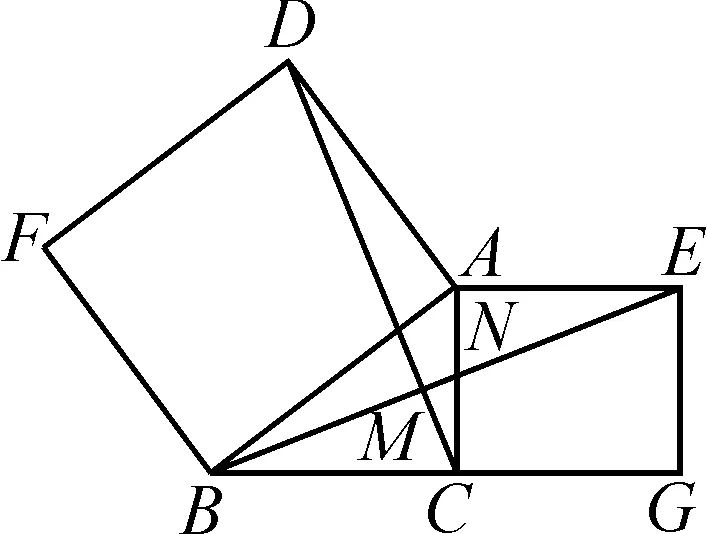
圖10
(3)如圖11,若點(diǎn)A在線段BC上,△ABD,△AEC都是等邊三角形,那么BE=DC嗎?若AD與BE交于點(diǎn)F,AE與CD交于點(diǎn)G,那么AF=AG嗎?△AFG是等邊三角形嗎?為什么?

圖11
3 架構(gòu)知識網(wǎng)絡(luò),疏通知識的連接點(diǎn),促進(jìn)學(xué)生高階思維的發(fā)展
在平時(shí)的教學(xué)中發(fā)現(xiàn),很多時(shí)候?qū)W生的知識處于斷點(diǎn)狀態(tài),解決問題時(shí)會出現(xiàn)不同程度的錯(cuò)誤,于是,筆者以發(fā)現(xiàn)的問題為切入點(diǎn),回歸課本,從教材中尋找知識間的內(nèi)在聯(lián)系,幫助學(xué)生疏通知識的連接點(diǎn),架構(gòu)知識網(wǎng)格,從而促進(jìn)高階思維的發(fā)展.

通過本題,筆者發(fā)現(xiàn)學(xué)生已有的知識是碎片化的,缺乏系統(tǒng)性和連續(xù)性.筆者認(rèn)為,要立足課本例題,搭建知識之間的橋梁,架構(gòu)起完全平方式、一元二次方程根與系數(shù)的關(guān)系,以及根的判別式和二次函數(shù)圖象與x軸交點(diǎn)個(gè)數(shù)之間縱橫相連的關(guān)系,使知識富有整體性、連續(xù)性、系統(tǒng)性,在此基礎(chǔ)上運(yùn)用知識去解決問題,提高高階思維能力.
例2若α,β是一元二次方程3x2+2x-9的兩根,分別求下列各式的值:
立足課本習(xí)題,設(shè)計(jì)這樣有層次性的題目,符合“人人都能獲得良好的數(shù)學(xué)教育,不同的人在數(shù)學(xué)上得到不同的發(fā)展的要求”的新課程理念,促進(jìn)高階思維的發(fā)展.
蘇霍姆林斯基在給《教師的建議》一書中“10 第一次學(xué)習(xí)新教材”認(rèn)為:“學(xué)生學(xué)業(yè)落后,成績不及格的根源之一,就是第一次學(xué)習(xí)新教材沒有學(xué)好……知識是在不停地發(fā)展的,對某段教材的學(xué)習(xí)將持續(xù)一段長的時(shí)間,對知識的每一次運(yùn)用,同時(shí)也是知識的發(fā)展和深入.而第一次學(xué)習(xí)新教材,是由不知到知、由不懂到理解事實(shí)、現(xiàn)象、性質(zhì)、特征的實(shí)質(zhì)而邁出的重要的第一步.” 所以,知識建構(gòu)對于學(xué)生新知的理解運(yùn)用有著舉足輕重的作用.
4 把握知識的實(shí)質(zhì),把握思維的生長點(diǎn),促進(jìn)學(xué)生高階思維的發(fā)展.
以問題為切入點(diǎn),回歸課本,反復(fù)揣摩知識的精髓,準(zhǔn)確掌握知識的實(shí)質(zhì)內(nèi)容,精準(zhǔn)把握學(xué)生思維的生長點(diǎn),促進(jìn)學(xué)生高階思維的發(fā)展,以適用未來時(shí)代發(fā)展的要求.
問題4(課本原題)圖12為某二次函數(shù)圖象的一部分,有如下四個(gè)結(jié)論:
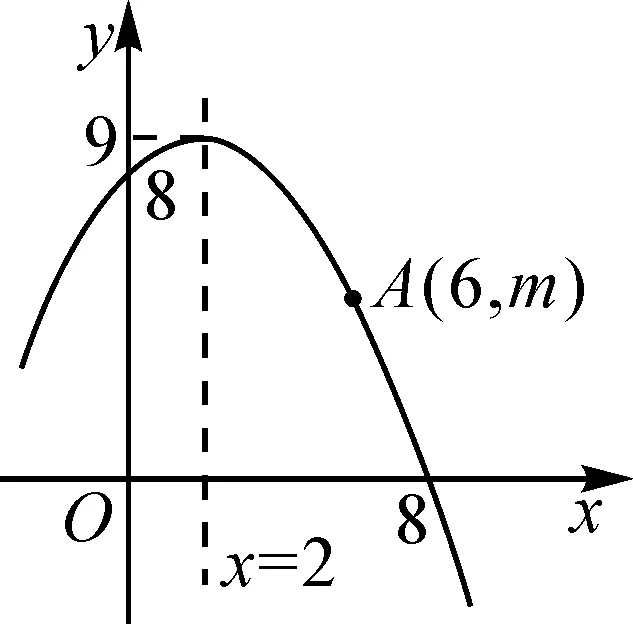
圖12
②若B(-1,n)在這個(gè)二次函數(shù)圖象上,則n>m;
③該二次函數(shù)圖象與x軸的另一個(gè)交點(diǎn)為(-4,0);
④當(dāng)0 正確結(jié)論的序號是( ). A.①③ B.①④ C.②③ D.②④ 學(xué)生解決本題時(shí)出現(xiàn)了很嚴(yán)重的錯(cuò)誤,這是由學(xué)生不熟悉二次函數(shù)圖象及性質(zhì)、缺乏幾何直觀、運(yùn)算能力和推理能力弱造成的.針對這個(gè)問題再次回歸蘇科版數(shù)學(xué)九年級下冊第26頁“學(xué)會‘讀’二次函數(shù)的圖象”一文,通過課本的再研讀,學(xué)生忽然有種柳暗花明之感. 課本是濃香的醇酒,是教學(xué)的根基,要多品,細(xì)品,慢品,在回味中不停思考,總結(jié),提高.Z

