巧解初中幾何問題
——以構(gòu)造輔助圓為例

徐 樂

? 江蘇省靖江市外國語龍馨園學校

圓是初中數(shù)學平面幾何中非常重要的一個知識點,與初中數(shù)學中其他幾何問題有著緊密的聯(lián)系.所以在解決幾何問題時,一些無法利用常規(guī)思路求解的綜合問題可以嘗試通過構(gòu)造輔助圓的方式來解決.因此,在初中數(shù)學幾何問題解題教學中,教會學生如何正確使用輔助圓來巧解幾何問題是教師需要重點研究的問題.下面將通過例題對輔助圓的應用進行說明.

1 角的問題

例1在△ABC中,AB=AC,∠ABC的平分線交AC于點D,已知BC=BD+AD,求∠A的度數(shù).

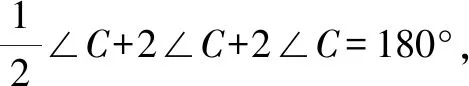
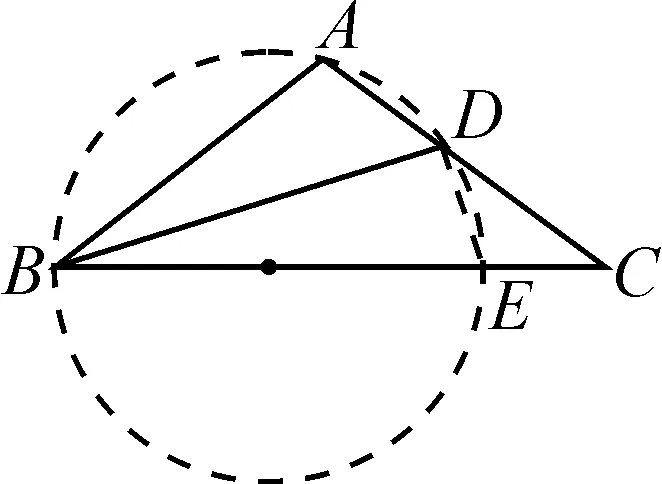
圖1

在初中數(shù)學幾何問題中構(gòu)造輔助線需要充分結(jié)合試題的情況來進行.本題中輔助圓的構(gòu)造就是結(jié)合了本題所給定的角平分線的關(guān)系,根據(jù)相等的圓周角所對應的弧和弦長相等的性質(zhì)來實現(xiàn);然后通過輔助圓及相關(guān)線段關(guān)系來與相關(guān)角取得聯(lián)系;最后利用三角形的性質(zhì)求解.教師要對學生進行相應的引導,讓學生掌握通過角的關(guān)系來構(gòu)造輔助圓,進而借助輔助圓解決問題.

2 線段長度的問題

例2如圖2所示,在Rt△ABC中,AB⊥BC,AB=6,BC=4,P是Rt△ABC內(nèi)部的一個動點,且滿足∠PAB=∠PBC,則線段CP的最小值為( ).

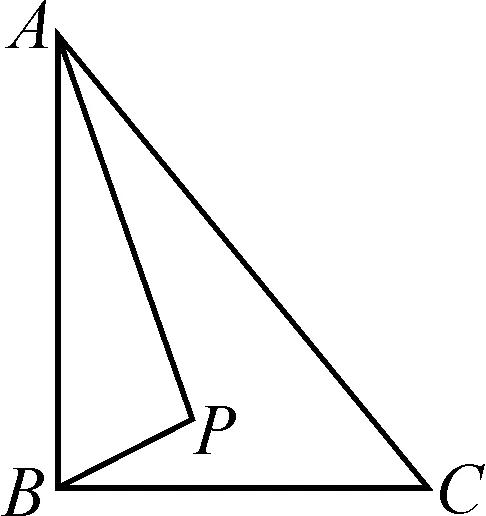
圖2

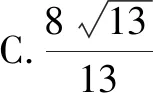
分析：根據(jù)AB⊥BC可以知道∠ABC=90°,結(jié)合∠PAB=∠PBC可得到∠APB=90°,所以△ABP是直角三角形.根據(jù)直角三角形中斜邊的中線等于斜邊的一半以及圓的直徑所對的圓周角是90°,可知點P在以AB為直徑的圓上.以AB的中點O為圓心,AB為直徑作圓,如圖3所示.這樣就可得到當PC的值最小時,點P正好在線段OC上.因為AB=6,所以O(shè)B=3.在Rt△OBC中,BC=4,根據(jù)勾股定理得到OC=5,于是可求出PC的最小值為2.所以正確答案是選項B.

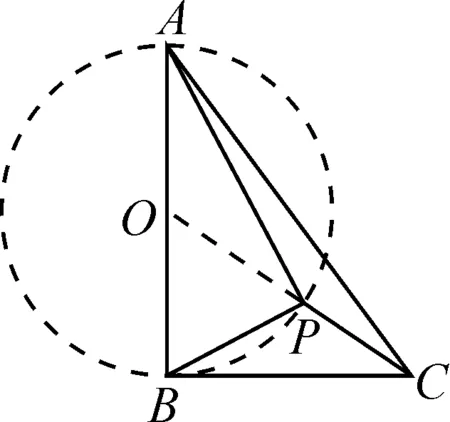
圖3

例2的解題關(guān)鍵是需要判斷點P的軌跡,首先根據(jù)試題中所給定的關(guān)系得到∠APB=90°,結(jié)合直角三角形的性質(zhì)和圓的性質(zhì)很容易判斷出點P在以直線AB為直徑的圓上,然后就能夠求解最小值.因此,在解題的過程中,只有認真分析題目條件,才能順利找到解題思路.教師在進行解題教學時需要教會學生如何根據(jù)題目中所給定的已知條件來進行分析,從而找到解題思路.很多幾何問題都是需要在解題的過程中才能夠找到相應的解題思路,并不是通過對試題的觀察就能得到解題思路的.因此結(jié)合已知條件來對試題中存在的關(guān)系進行分析,在解題的過程中發(fā)現(xiàn)解題思路,是解決問題最好的方式.教師需要引導學生先根據(jù)已知條件嘗試找到解題的思路,進而解決問題.

3 三角形相似的問題

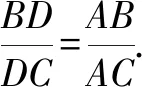
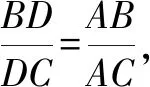
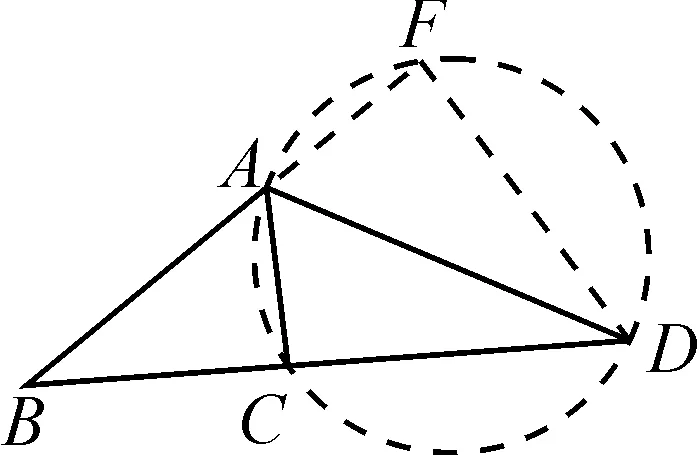
圖4

幾何問題中需要求證的結(jié)論存在線段比例關(guān)系或者線段等積關(guān)系時,都會涉及三角形相似或者全等的證明,通過構(gòu)造圓為三角形相似或者全等提供條件,實現(xiàn)對問題的求解.在這個過程中,需要充分結(jié)合例題1和例題2中輔助圓構(gòu)造的方式來找到相應的關(guān)系.

4 動點的問題

例4如圖5所示,邊長為3的等邊三角形ABC,D,E分別是BC,AC邊上的兩個動點,且BD=CE,AD,BE交于點P,求點P的運動路徑長和CP的最小值.

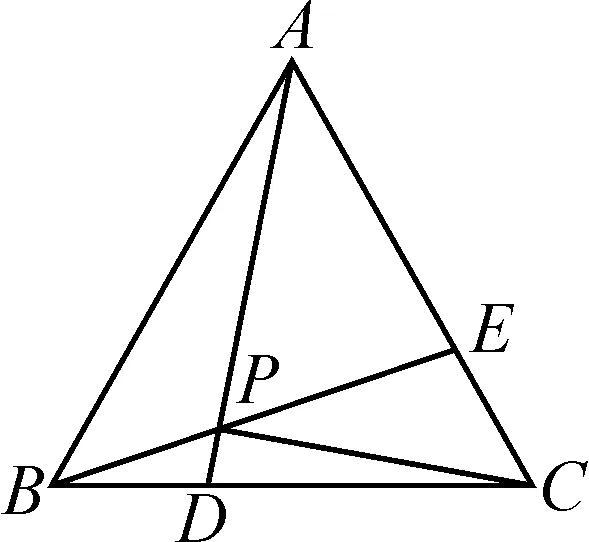
圖5

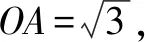
解：由AB=BC,∠ABD=∠BCE,BD=CE得△ABD≌△BCE.

由∠CBE+∠ABP=60°,得∠BAP+∠ABP=∠APE=60°.

所以∠APB=120°.

故點P的運動軌跡是以AB為弦的圓上的一段弧.

如圖6所示,作△ABP的外接圓,圓心為O,連接OA,OB,OP,OC.

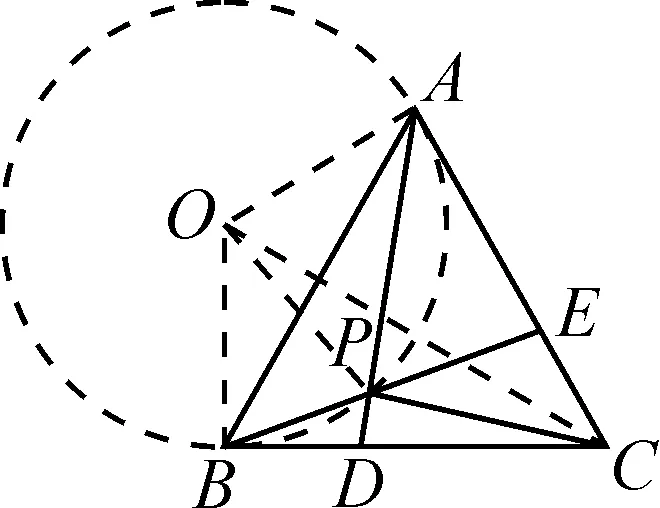
圖6

由OA=OB,AC=BC,得△AOC≌△BOC.

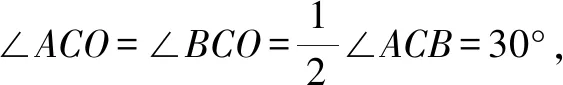
故∠OAC=90°.

在三角形的動點問題中,如果動點與一條線段所構(gòu)成的角度固定,則說明這個動點的軌跡是以這個線段為弦的圓上的一段弧,通過這個關(guān)系可以構(gòu)造輔助圓,然后利用圓的性質(zhì)來求解問題.本題給定的是正三角形,當然不同的三角形中所呈現(xiàn)的關(guān)系可能會存在差別,但是本質(zhì)沒有變化.例如,在例題2中通過計算所得到的角度為90°的特殊角,這個輔助圓的圓心就在直角三角形的斜邊上.例4中這個角度為120°,圓心在三角形的外部,通過輔助圓來充分利用圓的相關(guān)性質(zhì),能夠更好地對問題進行求解,實現(xiàn)問題的解決.

本文中對輔助圓在初中數(shù)學平面幾何中的應用進行了總結(jié),并通過相關(guān)例題對其用法進行了說明.在初中數(shù)學平面幾何問題中巧用輔助圓能夠優(yōu)化試題解法,實現(xiàn)快速求解.因此,教師在解題教學的過程中需要對學生進行有效地引導,讓學生掌握輔助圓的應用,從而提升解題能力;提升數(shù)學素養(yǎng).Z