幽默引人入勝 留白發人深省 結語繞梁三日
——初中數學課堂教學語言藝術提升研究

陳秀海

? 江蘇豐縣華山鎮華山初級中學

作為一名初中數學教師,如何在課堂教學語言上體現特色,發揮語言的魅力,讓數學教學更加深入淺出、通俗易懂,直接影響著數學課堂的質量.本文中就數學教學語言藝術提升問題著手進行研究分析[1].

1 幽默的講解吸引學生注意力

1.1 言之有趣,妙趣橫生

課堂的導入,特別是新課的導入,妙趣橫生的導語能吸引學生的注意力,讓其主動投入到數學學習之中.在講授“解任意三角形”時,筆者先問:“同學們,你們不過河能測出河面的寬度嗎?不上樹能量出樹高嗎?不走近敵方陣地能測得敵我雙方陣地之間的距離嗎?”接著指出:我們通過這節課學習“解三角形”就可以解決這些問題了.這樣的導入,能引起學生對所學內容的濃厚興趣.

1.2 言之有情,情理交融

知識本身是無情的,但是我們的教學是有情的.教師的任務就是將無窮的知識轉化到有情的教學過程中,讓知識變得有“文氣”“人氣”,讓學生能感受到知識的溫度,從而在接受知識的過程中不再冷淡.因此,課堂教學需要“有情”“有溫度”的語言.也許只有這樣,才能讓學生真正融入到教學中,感受到課堂的真正意義.

1.3 言之有啟,因勢利導

蘇霍姆林斯基曾說過:“教學的技巧并不在于能預見到課堂的所有細節,在于能根據當時的具體判斷,巧妙的在不知不覺中作出相應的變動.”課堂是多變的,其中一定存在著不可預設的意外,需要教師針對性的啟發引導,需要有一雙慧眼,透視課堂,敏銳捕捉.

1.4 言之有度,展示藝術

數學課堂教學語言藝術的風趣體現在教師獨具匠心的創造力上.嚴密的符號體系、獨特的公式結構、形象的圖象語言,如果用學生喜歡的、生動有趣的而又不失數學知識精髓的語言表達出來,那么數學課堂就不會再讓學生感到枯燥無味、繁瑣雜重.在教學過程中筆者也在想一些點子讓學生接受更簡單的數學知識,如編成諺語、古詩等樣式來引導學生掌握.例如,在學生解分式方程時,筆者編寫了“鋤禾日當午,同乘公分母,解個小方程,驗根解寫出”.

2 簡單的留白發人深省、促進思考

2.1 提問過程中的留白藝術

(1)教學語言嚴謹中不失留白

嚴謹,顧名思義,嚴肅謹慎,不但要求準確,更要體現規范.例如,在講述圓心角和圓周角的關系時,將圓周角頂點A的位置故意留白,引導學生體會弧BC所對的圓周角的位置關系,從而引導學生在理解點A的位置上體會嚴謹性.

(2)注重教學語言的靈活性

要用形象化的語言去解釋抽象的數學概念、數學公式.一般來說,對人的感官富有刺激性的語言,最能引起學生的興趣.在學習探尋數據規律時,筆者給學生展示了1+2+3+……+2 020,讓學生來計算,很多學生卻搖頭無語.其實,這個問題學生在小學三四年級就可以很簡單地計算出來了,現在怎么不會呢?筆者將梯形公式展示出來,結果同學們一驗證,還真是,從算法到意義,巧妙地將一些常見的公式用在復雜問題中,讓學生記憶深刻,終生不忘.

(3)注重教學語言的啟發性

要精心錘煉描述性的語言,把學生帶入美的意境,數學教學中偶爾出現幾句詩情畫意的語言,效果更是不同凡響.據說陳景潤的老師曾經用詩一般的語言向學生介紹了哥德巴赫猜想:自然科學的皇后是數學,數學的皇冠是數論,而哥德巴赫猜想則是皇冠上的明珠.他還意味深長地說:“昨天晚上,我做了一個夢,夢見你們中的一位同學了不得,他證明了哥德巴赫猜想.”這句話產生的神奇的力量,激勵陳景潤開始摘取皇冠明珠的萬里長征,他矢志不渝,百折不回,終于創造了數學的輝煌.

(4)注重教學語言的規范性

對于數學語言,要求得非常規范.常常出現的“除”與“除以”、“切線”與“切線長”等如果混為一談,就違背了同一律;又如有的教師講“圓中相等的圓心角所對的弧相等”“圓錐的體積等于圓柱體積的三分之一”,就忽略了“同圓或等圓”“同底等高”的條件;再如對“90°”和“垂直”兩個概念的理解,都必須用規范的語言進行說明.

2.2 講述過程的留白藝術

(1)情感方面的留白

情感留白,有時候在課堂上可以讓學生對問題更加關注,思考更認真,體驗更深刻,從而實現對數學文本的更深層次的理解與把握.例如,在講述銷售問題時,面對“要獲得利潤5 000元”,我們該怎么安排物品的售價呢?按照常規根本不能實現這一要求呀?怎么辦?在關鍵環節故意流露出難以解決的表情,激發學生的情感,與之共鳴,進一步調動學生的思考力.

(2)內容方面的留白

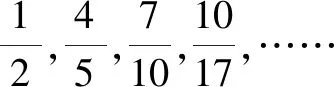
(3)問題研究的留白

問題留白,可以歷練學生的思維品質.針對一些問題,也可根據問題情境設計不同的留白,特別是在旋轉問題、動點問題的研究過程中,注意適時留白,讓學生自己來思考研究,這樣會給學生更多的表現機會.諸如像常見的“45°模型”“一線三直角模型”等,面對出現的疑問該怎么處理呢?將問題留白,引導學生小組內研究分析,找到方法并進行歸納,形成模型,讓學生能夠舉一反三.

3 巧妙的結語引導學生學思結合、拓展延伸

數學知識的前后聯系密切,特別是一些螺旋上升的知識串,更是交疊在一起的,講述過程需要逐步深入,循序漸進,讓學生在把握過程中進行類比,得到感悟與啟迪,如果語言再具有詩情畫意的感染與啟發性,那效果就會更好.

例如,在講述整式的加減運算過程中結合圖形探究整式規律性問題時,從簡單的問題提起,學生很容易把握,但是隨著數字的變化,學生的思維似乎變得遲鈍,于是就將要求變成“求救”:如果我要得到第100個圖形,怎么計算其中的個數呢?面對疑難求助,學生深入思考的力度就大了.再追問:第2 023個圖形呢?我們將這些具體的數字用字母替換一下會怎么樣呢?學生在分析過程中就會得到啟示,用字母表示數的思維變換就得到了推進,問題就會迎刃而解.

如果語言能將學生帶入詩情畫意之中,那么學生會更銘記深刻.據說我國數學家陳景潤曾用詩意的語言介紹哥德巴赫猜想,進一步激發學生的數學求知欲.

課堂的結語,往往是課堂知識精髓的最后呈現,體現的內容是重點、難點、關鍵點甚至是畫龍點睛的內容.巧妙的結語不僅讓學生對知識的記憶更加深刻,更能讓學生對所學知識進一步升華,似乎感覺余音繞梁,再有奮力探究的勁頭.

3.1 畫龍點睛式的結語

一堂課的結束,不能簡單地用幾句話做個總結就可以了,還需要深化課題內容,讓學生進一步得到余味,更要從這節課的主題思想中感受到數學的博大精深,將學生帶入到另一個層面的未知王國之中.在學習勾股定理后,展示了數學家畢達哥拉斯根據勾股定理所畫的“勾股樹”.當一個巨大的“勾股樹”展現在學生面前時,直觀的畫面讓學生眼前一亮.這種畫龍點睛之筆的結語雖然沒有鏗鏘的語言,但也讓學生產生震驚的同時,記憶深刻,感悟頗深[2]．

3.2 承上啟下式的結語

(1)知識上的承上啟下.問題是數學的心臟,可見提問方式的不同,取得的效果也不同.大多數的新知識都是在舊知識的基礎上延伸和發展的,在新舊知識的銜接處要注重提問的技巧,尤其在一些暗示性的問題上要尋求突破,將知識點上下貫通,從而使得學習有序鞏固落實.

(2)方法上的承上啟下.整個教學過程中,將課堂還給學生,放手讓學生自主學習,讓他們真正成為學習的主人.通過問題,引導學習從已有經驗出發,盡情表達對于知識的理解,真正感受到自己是學習的主人,哪怕有的學生只說一句,或者知道意思但表述不清楚的,都要給予充分的肯定和鼓勵.

(3)思維上的承上啟下.當學生對問題的把握不是很準確時,往往停留在原來的思維定勢之上.若采用承上啟下的引導,思維有了變通,新舊知識有了聯系,解決問題的設想就變得豐富多彩.如遇到求解兩條線段求和的最小值問題,往往想到“將軍飲馬”,看到類似“PA+kPB”形式求最值,通過思維定勢,會思考“胡不歸問題”與“阿氏圓”等等.當思維能夠承上啟下時,問題就會在解答過程中變得通透.

總而言之,課堂教學是教育者的人生舞臺,教學是一門永無止境的藝術,想在課堂之上真正實現知識的傳授,學生能力的培養,就要不斷提升課堂語言表達的藝術魅力.只有這樣,課堂才會煥發出生命活力,“柳暗花明”,這樣的課堂才能變得枝繁葉茂.