再談圓錐曲線與函數、不等關系的綜合考查
欒功 顏紫葉 肖玉霞







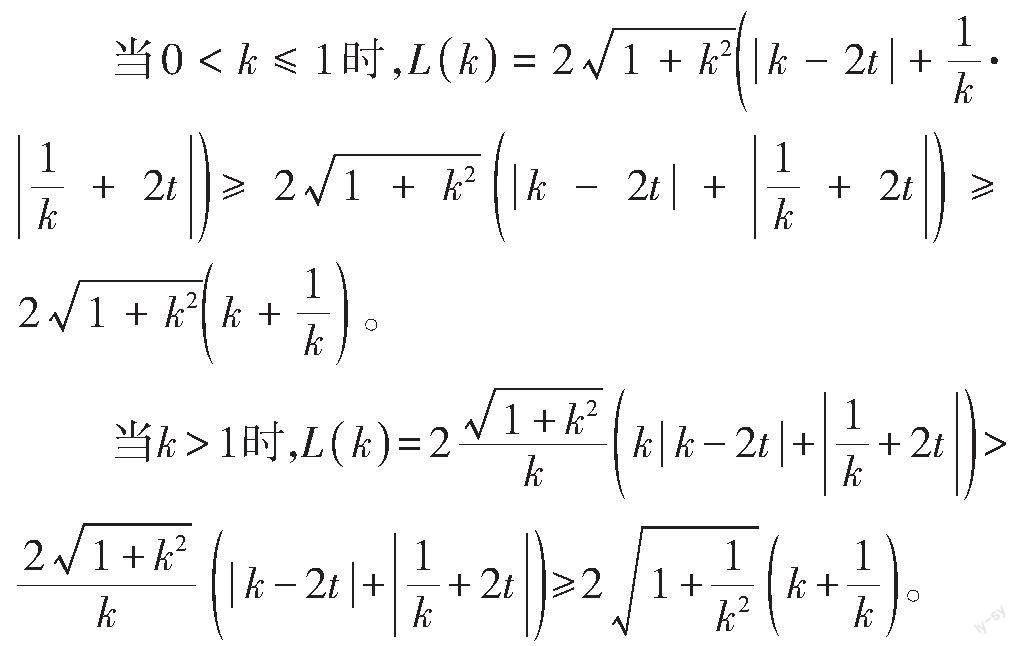

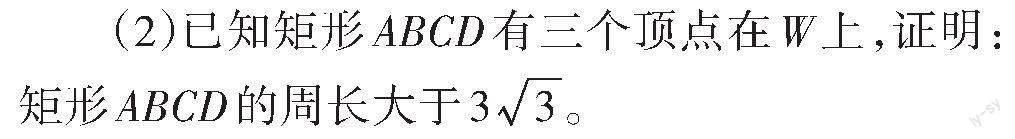

[摘 要]文章通過對2023年新高考Ⅰ卷數學第22題的解法進行探究,揭示了2023年新高考數學試題的一大新亮點:圓錐曲線與函數、不等關系深度綜合,為2024年高三數學復習備考提供參考。
[關鍵詞]圓錐曲線;函數;不等關系;綜合考查;新高考
[中圖分類號] G633.6 [文獻標識碼]? A [文章編號] 1674-6058(2023)26-0001-03
新時代背景下的教學改革與高考評價改革同向同行。隨著全國各省新一輪教材的使用,截至2023年7月,全國已有29個省份啟動新高考改革。近4年新高考數學試題的命題在逐步趨于穩(wěn)定的同時,突出了一些新的亮點。筆者在本刊2023年第20期的文章中以2023年全國甲卷理科第20題為例論述了2023年高考數學試題的一大亮點:解析幾何與函數深度綜合。下面筆者以2023年新高考Ⅰ卷數學第22題為例,再談2023年高考數學試題的另一大新亮點:圓錐曲線與函數、不等關系深度綜合。
一、 試題呈現
(1)求[W]的方程;
分析 試題第(1)問以考生熟悉的拋物線的定義為知識背景,考查拋物線的概念和求動點軌跡方程的基本方法;第(2)問將一個邊長可變的矩形與拋物線結合,考查矩形周長的最小化問題,看似是考生熟悉的弦長問題,實則極具創(chuàng)新性,將圓錐曲線中的弦長問題與絕對值函數、三角函數、導數研究函數的性質深度綜合,注重思維過程,突出考查考生的數學素養(yǎng),有助于拔尖創(chuàng)新人才的選拔。
二、試題溯源
題源1 (新人教A版數學選擇性必修第一冊第146頁“復習參考題3”第10題,圖略)已知直線與拋物線[y2=2pxp>0]交于[A],[B]兩點,且[OA⊥OB],[OD⊥AB]交[AB]于點[D],點[D]的坐標為[2,1],求[p]的值。
題源2 (2002年全國高中數學聯賽第13題,圖略)已知點[A0,2]和拋物線[y2=x+4]上兩點[B、C],使得[AB⊥BC],求點[C]的縱坐標的取值范圍。
題源3 (1998年上海市高中數學競賽第三大題,圖略)已知在拋物線[y=x2]上有一個正方形的三個頂點[A]、[B]、[C],求這個正方形面積的最小值。
題源1源于教材習題,與上述試題在幾何特征上有相同的本質,都是直角三角形與拋物線相結合,區(qū)別在于題源1是確定性問題,而上述試題是雙動點問題,源于教材而高于教材,起到引導教學、回歸教材的作用。題源2與題源1相比,由確定性問題上升為動態(tài)問題。題源3與上述試題幾乎相同,歷年的競賽試題往往蘊含著豐富的數學思想方法,一線教師需引起重視。
三、 解法探究
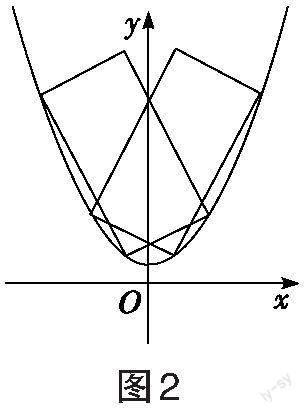
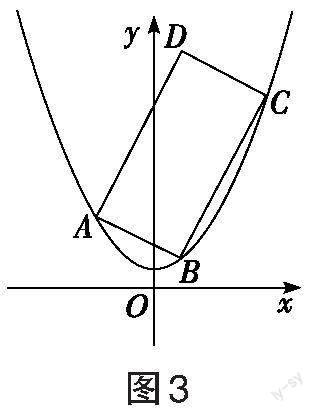
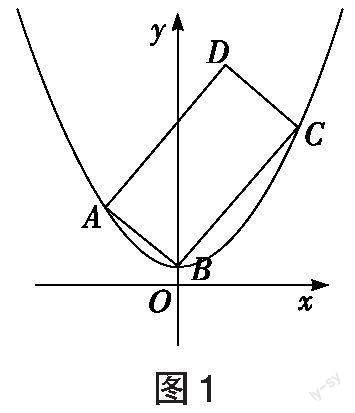
對于復雜的問題,考生可先從較為特殊的情況入手探尋思路。如圖1所示,本題最特殊的情況就是矩形有一個頂點和拋物線的頂點重合,與題源1相同,考生自然清楚這是關于直線[BC]斜率[k]的函數問題。由于本題中矩形與拋物線搭接形式的開放性,我們需要順勢思考更為一般的情況。如圖2所示,矩形的四個頂點有三個頂點在拋物線上,則這三個點不可能同時出現在[y]軸的同側,結合拋物線的對稱性,從邏輯意義上我們不妨只考慮圖3的情況,記點[A、B、C]在拋物線上,且點[A]在[y]軸的左側,點[B]、[C]依次出現在[y]軸的右側。下面從不同角度設參求解。
評析:設線求解弦長是解答這類問題的通性通法,大部分考生都會想到這一步,解題困難主要在于矩形周長取值范圍的求解。由于矩形邊長的可變化性,致使矩形周長的表達式出現了雙變量,這讓絕大部分考生望而卻步。該解法選擇先固定主元再求解的思路,是解決雙變量問題的常見方法。在具體的函數最值求解過程中,不論是去絕對值的分類討論,還是運用導數求解目標函數的單調性,都將函數與圓錐曲線的綜合體現得淋漓盡致。試題命制之新穎,解答之根本,都無不讓人贊嘆不已。
評析:該解法建立在洞悉試題背后的數學本質之上,通過兩個“不妨設”和代數代換,避免了解法1的分類討論,體現了“多想少算”的命題意圖,對考生的數學思維能力要求較高。
評析:該解法的本質是借助直線的方向向量探尋矩形[ABCD]有三個頂點落在拋物線上的充要條件,對考生的動態(tài)思維能力和化歸與轉化問題的能力要求較高。
四、 回顧反思
回顧以上解法,解題思路皆源于對相關數學概念本質的理解,進一步探究,便有如下思考:
我們可做如下嘗試:
這里巧妙地借助[k]的范圍對表達式進行初步放縮,從而接著利用三角不等式放縮消元,將二元函數問題轉化為一元函數問題。試題巧妙地將解析幾何、函數、不等關系融合在一起,加大了對數學思維的考查,為不同層次的考生發(fā)揮水平提供了空間。
思考3 新時代下的高三數學復習教學的重心在哪里?從解題分析來看,試題的命制源于基礎性、本源性知識,發(fā)展于各知識模塊之間的聯系。從新高考試題體現的這兩大亮點來思考,高三復習教學的重心應落在基本概念、公式、原理等本源性知識的理解上,落在知識體系的構建上,落在學生思維能力的培養(yǎng)上。當然,高一、高二基礎年級的教學更應如此。
[? ?參? ?考? ?文? ?獻? ?]
[1]? 2002年全國高中數學聯賽[J].中等數學,2002(6):19-24.
[2]? 李大元,劉鴻坤,熊斌,等.1998年上海市高中數學競賽[J].中等數學,1999(3):28-29.
[3]? 教育部教育考試院.高考試題分析:數學:2024年版[M].北京:語文出版社,2023.

