基于模型預測控制的風儲聯合電場參與電網二次調頻策略
劉傳斌, 矯文書, 吳秋偉, 陳 健, 周 前
(1.山東大學 電氣工程學院,濟南 250061; 2.清華大學 清華伯克利深圳學院;清華深圳國際研究生院,廣東 深圳 518055; 3.國網江蘇省電力有限公司電力科學研究院,南京 211100)
隨著電力電子技術的發展,風力發電(簡稱風電)技術取得了迅速進步,風力發電機結構已從最開始的定槳距結構發展為變槳距結構.變槳距結構捕獲風能效率較高,在高風速下風能利用率更高,變槳距調節逐漸成為兆瓦級以上風力發電機參與二次調頻的研究重點.儲能系統由于快速響應、精準跟蹤的特性,配合風電機組參與電網調頻,能夠有效提高電網二次調頻的效果.
雙饋異步風力發電機(Doubly Fed Induction Generator,DFIG)通常運行在最大功率點跟蹤(Maximum Power Point Tracking,MPPT)控制狀態,風力發電機轉子轉速與電網頻率完全解耦,不具備類似于同步發電機的慣性響應和長時間調頻能力.因而,高滲透率風電接入電力系統時會引起電網調頻能力不足等問題[1].針對這些問題,國內外的電網并網導則中均明確指出并網風力發電機須提供調頻服務[2].因此在電網進行二次調頻時,風力發電機需運行在減載模式,以便及時響應系統頻率變化,維持頻率穩定.目前,風力發電機參與調頻的基礎控制方式包括虛擬慣性控制、轉子轉速控制和槳距角控制3種[3].高滲透率風電的電力系統面臨嚴峻的調頻負擔,而且風場可以提供的調頻容量有限,因此亟需新的調控手段.例如,風電場輔以儲能系統,借助儲能系統的快速響應能力,可以減少風場的減載備用功率,快速響應電網二次調頻的要求[4].
近年來,研究者對風力發電機參與電網頻率調節進行大量研究并取得了可觀成果.文獻[5]中利用風力發電機中電力電子器件對功率的快速控制能力為頻率的偏移提供了短時有功支撐.文獻[6-7]中利用變流器快速的功率調節能力,通過釋放風力發電機轉子的動能,增強系統慣性.但是最大功率跟蹤會影響虛擬慣性控制,轉子動能提供頻率支撐能力有限,因此轉子控制策略只能提供短時的有功功率支撐并容易產生頻率的二次跌落問題.為了提升風力發電機持續提供有功功率的能力并解決頻率二次跌落問題,研究者提出了槳距角控制方案和風儲聯合調頻控制方案.文獻[8]中提出了一種根據上級系統命令控制槳距角的調頻控制策略,使風力發電機具備在復雜工況下連續運行的能力;文獻[9]中提出將儲能系統加入風電場中進行頻率控制,解決頻率的二次跌落問題.文獻[10]中在考慮儲能單元荷電狀態(State of Charge,SOC)基礎上提出風儲控制策略,此方案結合風力發電機槳距角的功率調節能力與儲能系統的快速響應能力,提高了風電并網穩定性,為本文選取槳距角控制方法提供了借鑒.現有儲能系統參與電網二次調頻的控制策略包括:基于SOC實施功率分配,在滿足儲能系統總體功率調節需求的同時,確保各儲能單元SOC滿足預期目標[11];基于SOC采用部分儲能單元以最優SOC運行,其他儲能單元最大出力運行的方式實施功率分配[12].文獻[13]中基于SOC對電化學儲能系統的各單元進行控制,與風力發電機協調進行一次調頻.這些策略都是分別考慮風力發電機和儲能系統參與電網一次調頻,沒有對風場和儲能系統統一進行二次調頻,而且上述控制策略處理約束條件的能力較差,不具有最優性.模型預測控制(Model Predictive Control,MPC)是一種最優控制技術,可以很好地解決多約束條件下的優化問題.
綜上所述,現有研究多關注風電場的一次調頻,關于二次調頻的研究很少.因此,合理解決風電場的頻率控制問題,在兼顧穩定性的前提下使得風力發電機具備充足的二次調頻能力,并且實現風電場和電化學儲能系統協調參與電網二次調頻,是需要進一步深入研究的內容.
通過分析風力發電機的機械特性和電化學儲能系統的運行特性,利用風力發電機在槳距角減載運行方式下輸出功率的可調性,本文建立基于風力發電機和儲能系統參與電網二次調頻的預測模型,提出一種基于MPC的風儲聯合電場參與電網二次調頻策略.該控制策略在保證風電場支撐電網頻率調整的基礎上,更好地分配了風電場內各風力發電機的有功出力,避免風力發電機的槳距角過度變化,減少了風能損失.此外,該控制策略充分發揮了電化學儲能系統的輔助調頻能力,進一步減少了風能損失,保障了對電網頻率的支撐.
1 雙饋風力發電機參與電網二次調頻控制方式
通常,風力發電機運行于最大功率跟蹤模式,當電網頻率發生跌落時,無法提供額外的有功功率支撐來參與電網二次調頻.因此,風力發電機須采用減載措施以獲取足夠的有功備用[14].
槳距角控制的調節能力較強,調節范圍也較大,可以實現全風速下的功率控制,而且變槳距控制系統可以提高風力發電機的風能利用率,可以減小陣風、載荷波動對風力發電機造成的影響,并與二次調頻的時間尺度吻合.風電場運行在最大功率跟蹤模式下,提供二次調頻的功率裕量極少,因此為了實現風力發電機獲得足夠有功備用的目標,依據風力發電機所處的風速,采取設置初始槳距角的方法,使風力發電機運行于減載模式下.
雙饋風力發電機通過調整槳距角和轉速,可在較大風速范圍內實現20%~100%額定容量的有功調節,調節范圍如圖1所示,其中v為風速,WTG表示風力發電機.
槳距角控制是在保持葉尖速比始終在最優值時通過調節風力發電機葉片槳距角,控制風力發電機捕獲得到的機械能,從而實現風力發電機有功功率控制.圖2為槳距角控制下風力發電機的運行點變化過程,其中Pm為機械功率,ωr和ωmax為轉子轉速及其最大值,θ1~θ4為風力發電機槳距角.當風力發電機工作于最大功率跟蹤模式時,風力發電機工作于運行點A,對應槳距角為0°,捕獲的機械功率為Pmax.當風力發電機的有功控制指令下降至Pcmd1、Pcmd2和Pcmd3時,風力發電機應上升槳距角使得其捕獲的機械功率下降,對應的運行點為B、C、D.當風力發電機有功控制指令在Pmax與Pcmd3之間時,風力發電機應工作于曲線ABCD上,且所有調節過程均為可逆.
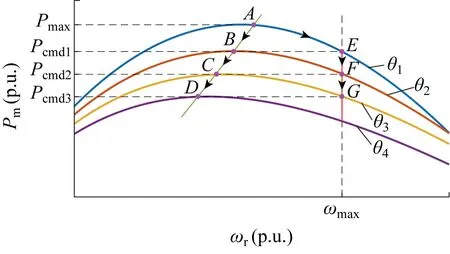
圖2 恒定風速下風力發電機機械功率曲線
由上可知,可通過調整槳距角來改變風能利用系數,這種控制方式能夠穩定地改變風力發電機輸出功率,從而為二次調頻提供有功支撐.本文建立基于槳距角控制的風電場的預測模型和儲能系統的預測模型,在控制過程中,MPC控制器收集來自各個風力發電機和儲能系統的測量值,預測其動態變化,并調節風力發電機和儲能系統的有功功率輸出,以實現控制目標.根據上級系統的有功功率指令值和風力發電機實際輸出功率之間的差值對槳距角控制進行修正,使得風力發電機在二次調頻期間能夠更好地調整槳距角來改變風力發電機出力,以此達到上級系統的功率指令值.
2 風儲聯合電場的預測模型
2.1 風力發電機的模型
根據空氣動力學模型,風力發電機捕獲的機械功率為
(1)
λ=wrR/v
(2)
式中:ρ為空氣密度;θ為槳距角;R為風輪機半徑;λ為葉尖速比;Cp為風能利用系數,可表示為[15]
(3)
考慮槳距角控制時,在風速變化的同時,風力發電機轉速也隨之變化,葉尖速比在小范圍內變化,因此可以將葉尖速比設為定值.對式(3)進行簡化,得到Cp關于θ的數學表達式:
Cp=0.22 (1 450θ-1-4.06θ-3-
0.4θ-5)e-12.5(12.5θ-1-0.035θ-3)
(4)
將式(4)代入式(1),可得:
0.4θ-5)e-12.5(12.5θ-1-0.035θ-3)]
(5)
當風電場處于中高風速下采取槳距角控制時,調頻的時間尺度較短,為了簡化模型,設定風速一直保持在某個較高的值不變.當風速一定時,可以得到風力發電機捕獲的機械能和槳距角近似的線性關系為[16]
Pm=k0θ+b
(6)
式中:k0為線性關系的系數;b為常數.
在一個槳距角控制周期內,槳距角可表示為
θ=θ0+Δθ
(7)
式中:θ0為初始槳距角;Δθ為槳距角變化量.
進而式(6)可以表示為
ΔPm=k0Δθ
(8)
式中:ΔPm為風力發電機機械功率變化量.
風力發電機槳距角控制的響應較緩慢,其傳遞函數可等效為一階傳遞函數,即
Gθ(s)=1/(1+Tθs)
(9)
式中:Tθ為槳距角控制響應時間常數;s為自變量.
進而可以得到Δθ和槳距角變化量參考值Δθref之間的關系:
Δθ=ΔθrefGθ(s)
(10)
風力發電機內部損耗等問題導致風力發電機捕獲的風能不能全部轉化為電磁功率,兩者之間的轉化關系可以用一階傳遞函數表示:
(11)
式中:ΔPe為電磁功率變化量;T為時間常數.
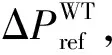
(12)
風場內的每臺風力發電機i的預測模型可以表述為
(13)
(14)
(15)
式中:Ai、Bi、Ci為參數矩陣;Δxi為狀態變量矩陣;Δyi為輸出變量矩陣,包括槳距角、風力發電機機械功率、電磁功率的變化量;Δui為控制變量矩陣,包括槳距角和電磁功率變化量參考值.
2.2 儲能系統的模型
為研究儲能系統分配的調頻功率與儲能單元SOC的關系,建立儲能系統的預測模型.在充放電過程中儲能單元的SOC一直變化,可由下式表示:
(16)
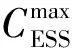
(17)
(18)
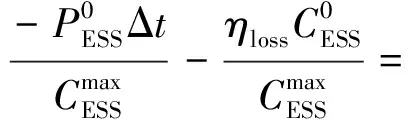
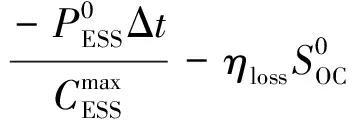
(19)
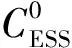
(20)
(21)
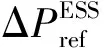
(22)
(23)
(24)
式中:AE、BE、CE和EE為儲能系統的參數矩陣;ΔxE為儲能系統的狀態變量矩陣;ΔyE為儲能系統的輸出變量矩陣,包括電池SOC、儲能系統輸出功率的變化量;ΔuE為儲能系統的控制變量矩陣,包括儲能系統的輸出功率變化量參考值.
2.3 風儲聯合電場的模型
基于風力發電機和儲能系統的模型,風儲聯合電場的連續狀態空間模型可以表述為
(25)
(26)
式中:A、B、C和E為風儲聯合電場的模型的參數矩陣;下標NC和E分別表示風電機組的數目和儲能系統.
基于連續狀態空間模型,轉化為采樣時刻為ΔTP的離散時域狀態空間模型:
(27)
(28)
式中:G和H為離散時域狀態空間模型的參數矩陣;Δu(k)為k時刻的控制變量.
3 基于MPC的調頻優化控制策略
風電場在響應二次調頻指令之前,需要保持減載運行模式,留有足夠的有功備用,故風電場中各風力發電機根據所處位置的風速以不同初始槳距角運行.在二次調頻過程中,如果風電場控制器向風力發電機調度相同的有功功率指令值,會出現槳距角變化過大情況,造成更多風能資源損失.因此需要優化各風力發電機的有功分配,設計合適的控制策略.在此基礎上,為了進一步減少風能損失,減小槳距角變化量,引入儲能系統減少風力發電機的減載備用功率,提出一種基于MPC的優化分配控制策略.
3.1 MPC控制原理
MPC是一種應用廣泛的控制方法[19-22],在每一個采樣時刻,根據獲得的當前測量信息,在線求解一個有限時間開環優化問題,并將得到的控制序列第一個元素作用于被控對象.在下一個采樣時刻,重復上述過程,用新的測量值作為此時預測系統未來動態的初始條件,刷新優化問題并重新求解,MPC的原理如圖3所示,t0為初始時間.為了準確預測風電場的動態變化,需要設置合適的控制周期Tc和預測周期Tp.控制周期要小于預測周期,而且大于采樣時間間隔ΔTP,預測周期由風電控制系統的動態性能決定.
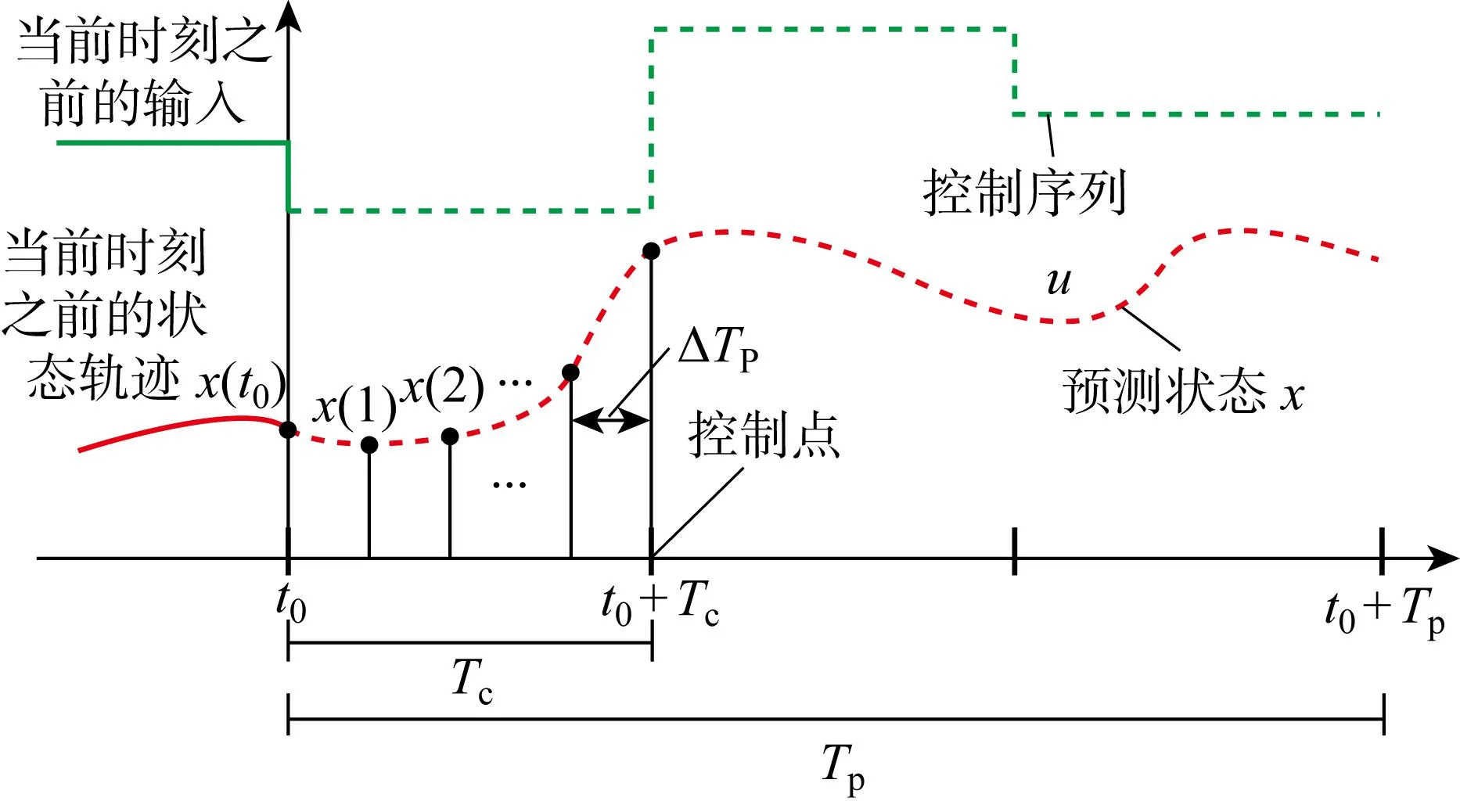
圖3 模型預測控制的原理
3.2 MPC優化策略
建立基于MPC的槳距角控制策略的優化問題,包括約束條件和目標函數.第1個控制目標為最小化風力發電機之間槳距角的差距以保證風電場中每一臺風力發電機的穩定運行.在只采用第一個控制目標的情況下,即風力發電機之間的槳距角差異最小化,這意味著所有風力發電機的槳距角都收斂到同一值.第2個目標函數為減小風力發電機自身的槳距角變化量,目的是最大限度地減少風能損失[8].第3個目標函數為使儲能系統留有足夠的充放電功率裕量,結合儲能電池SOC,基于SOC初始值、實際充放電時間和SOC期望值等,可以維持儲能電池在較好的SOC內,有效改善調頻效果,且在一定程度上降低了儲能電池輔助調頻的容量配置需求,對儲能電池規模化應用到電網調頻中具有一定意義[23-24].
風電場的兩個目標函數分別為
(29)
(30)
電化學儲能系統的目標函數為
(31)
總的目標函數是風場和儲能系統的目標函數按照權重系數劃分后相加:
(32)
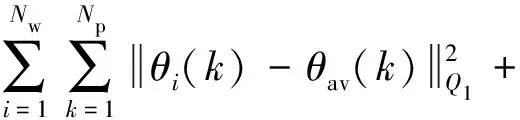
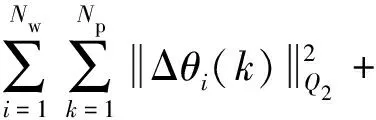
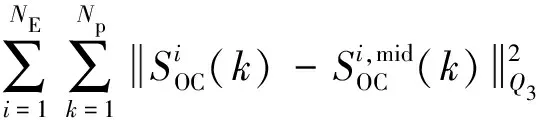
(33)
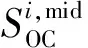
(34)
(35)
(36)
(37)
3.3 槳距角結構的改進
為準確達到上級系統的功率指令值,采用槳距角修正方案,通過引入槳距角補償值,使風力發電機能響應頻率變化達到上級系統下達的指令值.采用如圖4的控制結構,簡化了利用槳距角進行調頻的控制方案.
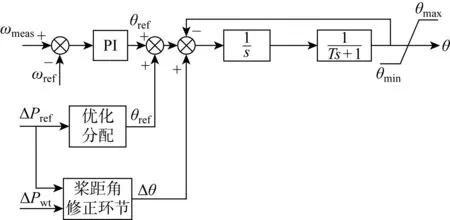
圖4 槳距角控制結構
傳統槳距角的控制指令是轉子的額定轉速ωref和實際轉速ωmeas,為了嚴格追蹤上級下達的有功功率指令值,槳距角控制方案在傳統槳距角控制的基礎上添加了槳距角響應功率指令環節和槳距角修正環節,其中槳距角修正環節的控制指令是風力發電機的有功功率參考值ΔPref和實際輸出的有功功率值ΔPwt.控制過程為:首先根據當前風速下的ΔPref值確定機組完成調頻任務所需槳距角變化量參考值Δθref;由于模型的簡化會產生誤差,所以引入槳距角修正環節,然后根據當前風速下風力發電機的ΔPref和Δpwt的差值,確定槳距角修正量Δθ,從而調節風力發電機的槳距角值θ.
當需要風電場參與調頻時,上級系統根據頻率恢復至額定值所需的功率缺額給風電場下達有功功率指令值,使風電場在不影響到電網穩定的前提下對電網提供有功支撐,完成二次調頻的任務.
4 案例分析
圖5為典型風儲聯合電場的結構圖,風電場經由33 kV/110 kV變壓器,再由20 km、110 kV的架空線連接到外部110 kV的交流電網中.風電場由10臺風力發電機、兩條饋線組成,每條饋線上連接5臺額定容量為5 MW的風力發電機,并且每臺風力發電機之間的距離為2 km.風場中每臺風力發電機的風速為13 m/s,初始槳距角為5°,電化學儲能系統的儲能容量為5 MW,二次調頻功率參考值為35 MW.
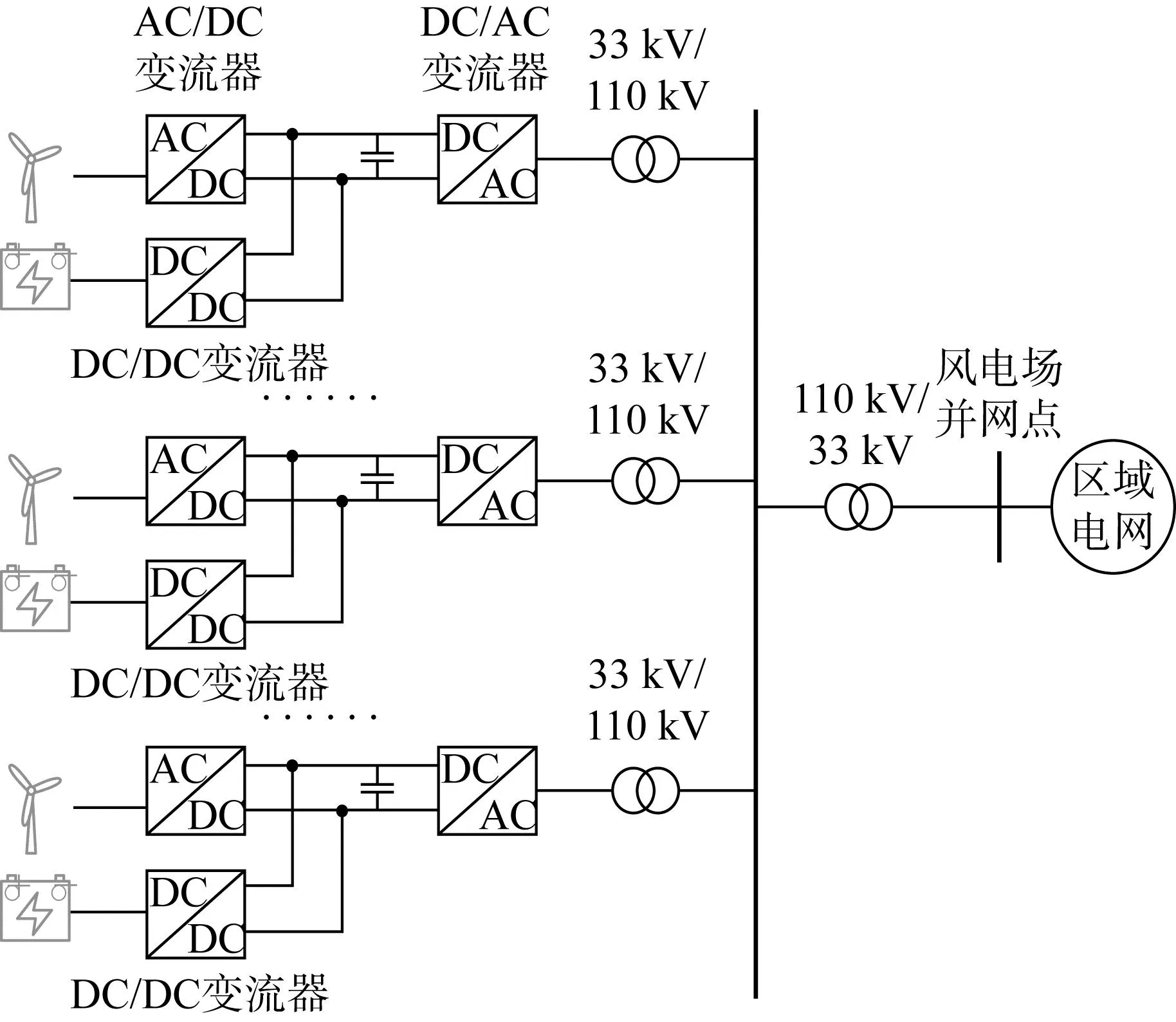
圖5 風儲聯合電場結構
圖6為在平均分配策略下,風電場內每臺風力發電機分配到上級系統發出的有功功率追蹤指令值均為0.7(p.u).圖7為平均分配策略下各風力發電機的槳距角參考值,由于上級系統發給每臺風力發電機的有功功率指令值是相同的,所以風力發電機的槳距角均將收斂至同一值.
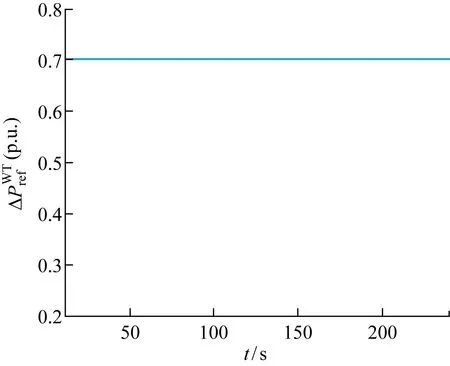
圖6 平均分配策略的各臺風力發電機的功率指令值
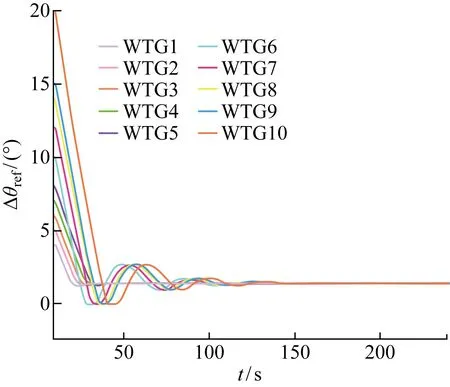
圖7 平均分配策略下的槳距角參考值
圖8為風電場在接受到上級系統下達的有功功率追蹤指令值后,根據不采用MPC的一步優化分配策略得到各風力發電機所分配的有功功率指令值,此時功率指令值根據優化策略中目標函數1和目標函數2得到.圖9為各風力發電機在一步優化策略下的槳距角參考值.

圖8 優化分配策略下的風力發電機有功功率指令值
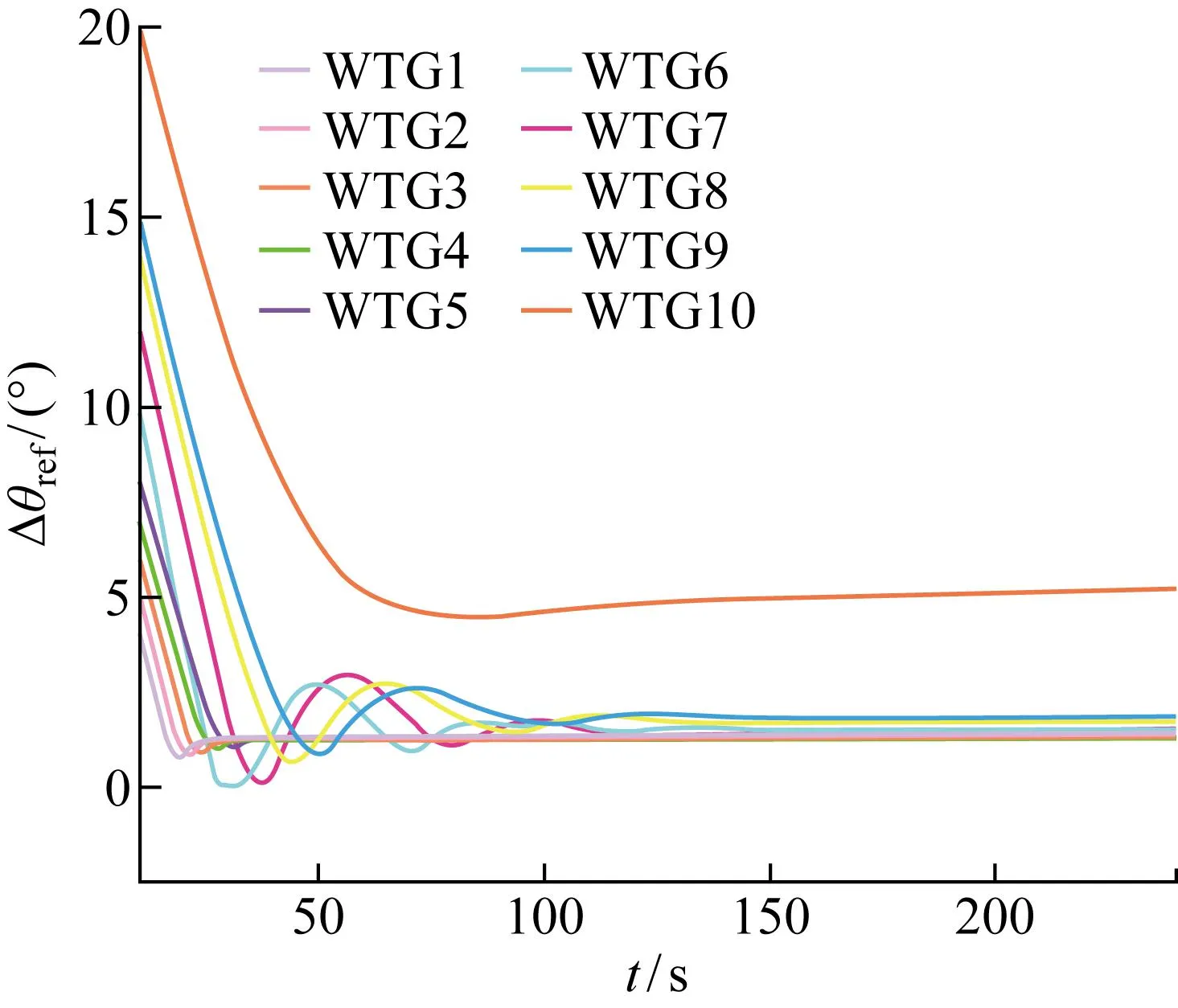
圖9 優化分配策略下的槳距角參考值
圖10和圖11分別為基于MPC優化策略當不考慮儲能系統時風電場各風力發電機的有功功率參考值和槳距角參考值.
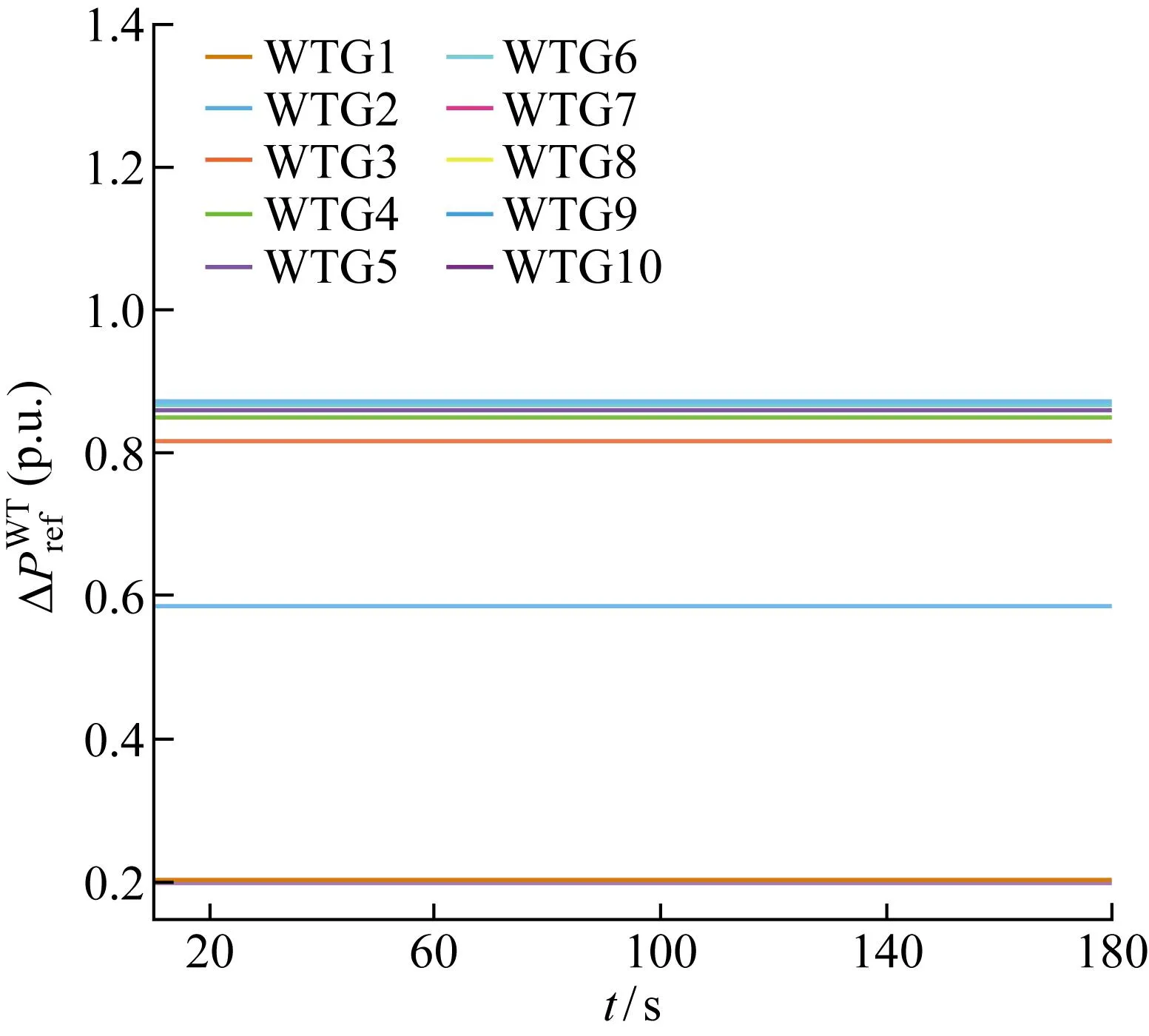
圖10 基于MPC不含儲能的風電場優化策略的有功功率參考值
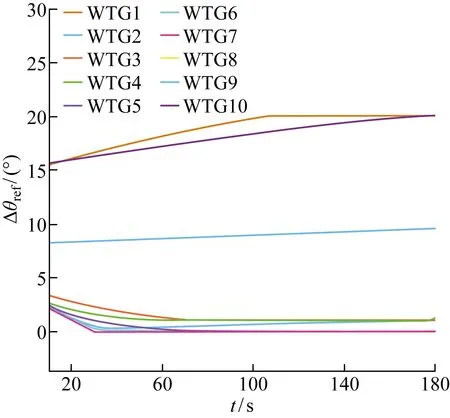
圖11 基于MPC不含儲能的風電場優化策略的槳距角參考值
因為電網下發的功率指令值超過儲能系統的容量,所以需要風電場和儲能系統聯合參與電網的二次調頻,此時3個目標函數的權值設置為:Q1>Q3>Q2.圖12和圖13分別為在基于MPC含儲能風電場優化策略下有功功率參考值和風力發電機的槳距角參考值,圖14為基于MPC優化策略的儲能系統有功功率值.由圖14可知,儲能系統留有足夠的充放電功率裕度,由于儲能系統的變流器響應時間常數比風力發電機變槳結構響應時間常數更小,所以儲能系統的響應速度比風力發電機更快.
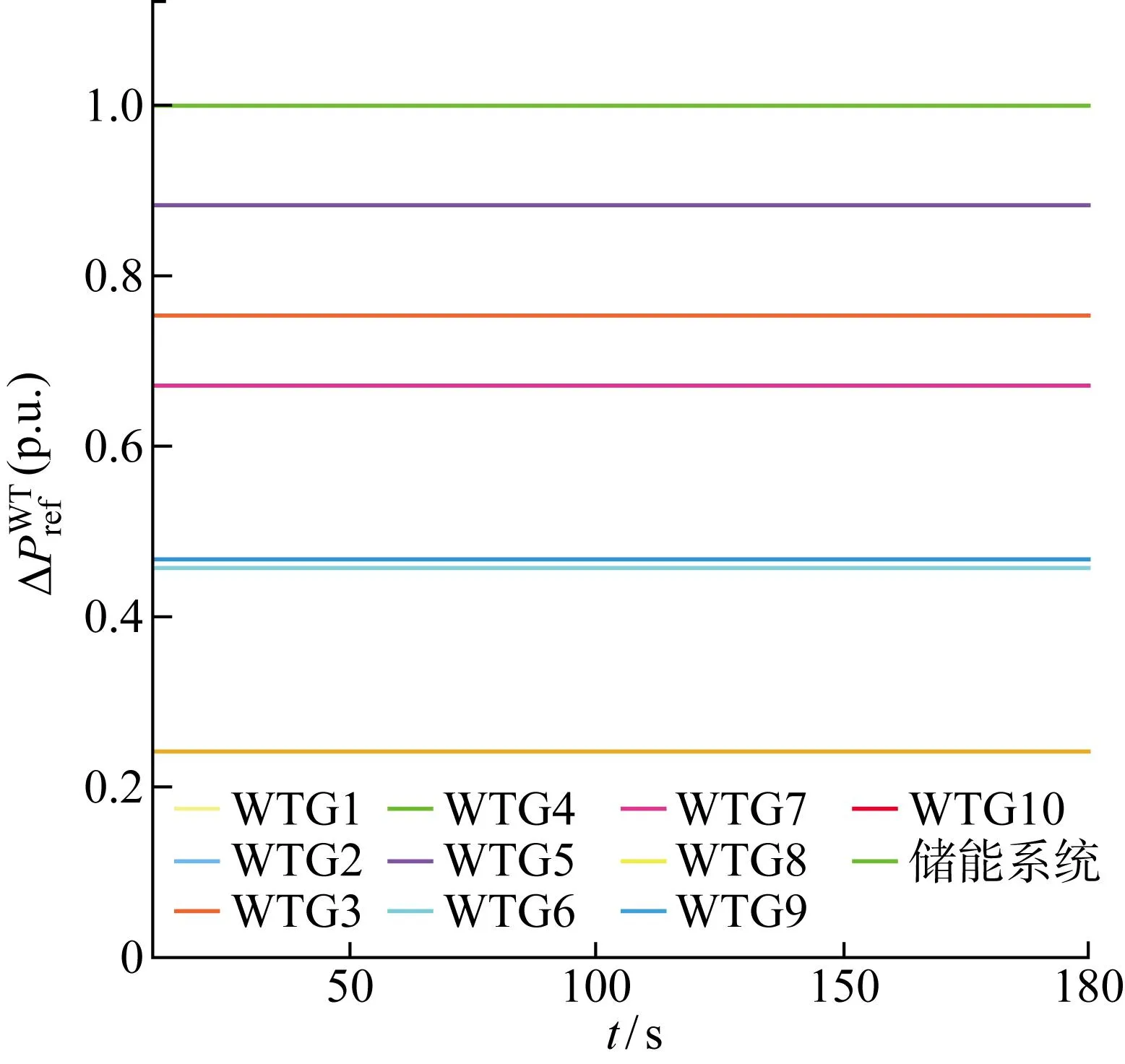
圖12 基于MPC含儲能的風電場優化策略的有功功率參考值
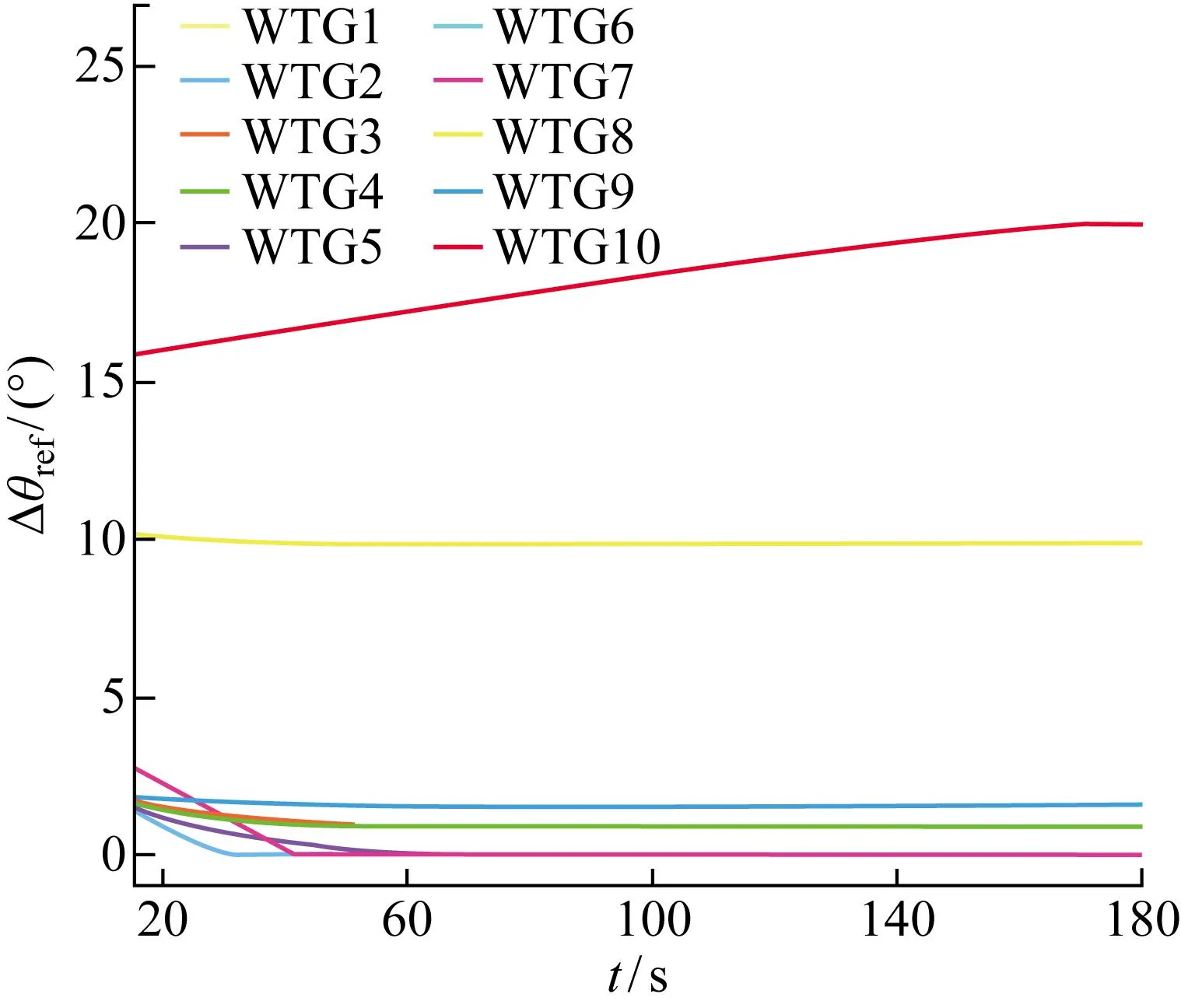
圖13 基于MPC含儲能的風電場優化策略的槳距角參考值
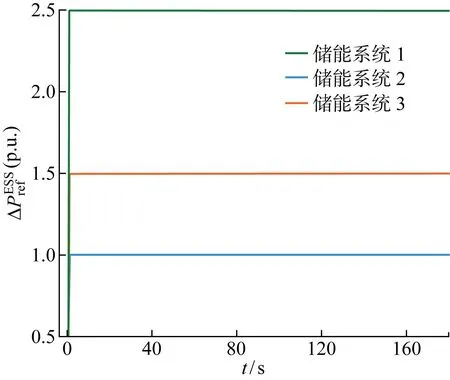
圖14 基于MPC優化策略的儲能系統有功功率
根據圖15可知,基于MPC含儲能優化策略的槳距角變化量不僅少于平均分配策略和一步優化策略下的槳距角變化量,同時還少于基于MPC不含儲能風電場優化分配策略下的槳距角變化量.在基于MPC含儲能風場的優化分配策略下,儲能系統快速響應、精確跟蹤的能力減少了槳距角的變化量,節省了調節時間,加快了控制速度,進而減緩了槳距角機械機構的損耗.而在圖16中的仿真結果可以看出,風力發電機采用平均分配、一步優化分配、基于MPC不含儲能風電場的優化分配和基于MPC含儲能風電場的優化分配策略追蹤到功率參考值用時分別為120 s左右、100 s左右、80 s和50 s,基于MPC含儲能風電場的優化分配控制策略達到指令值速度更快的同時功率追蹤過程比其他3種策略的功率追蹤過程更加穩定.
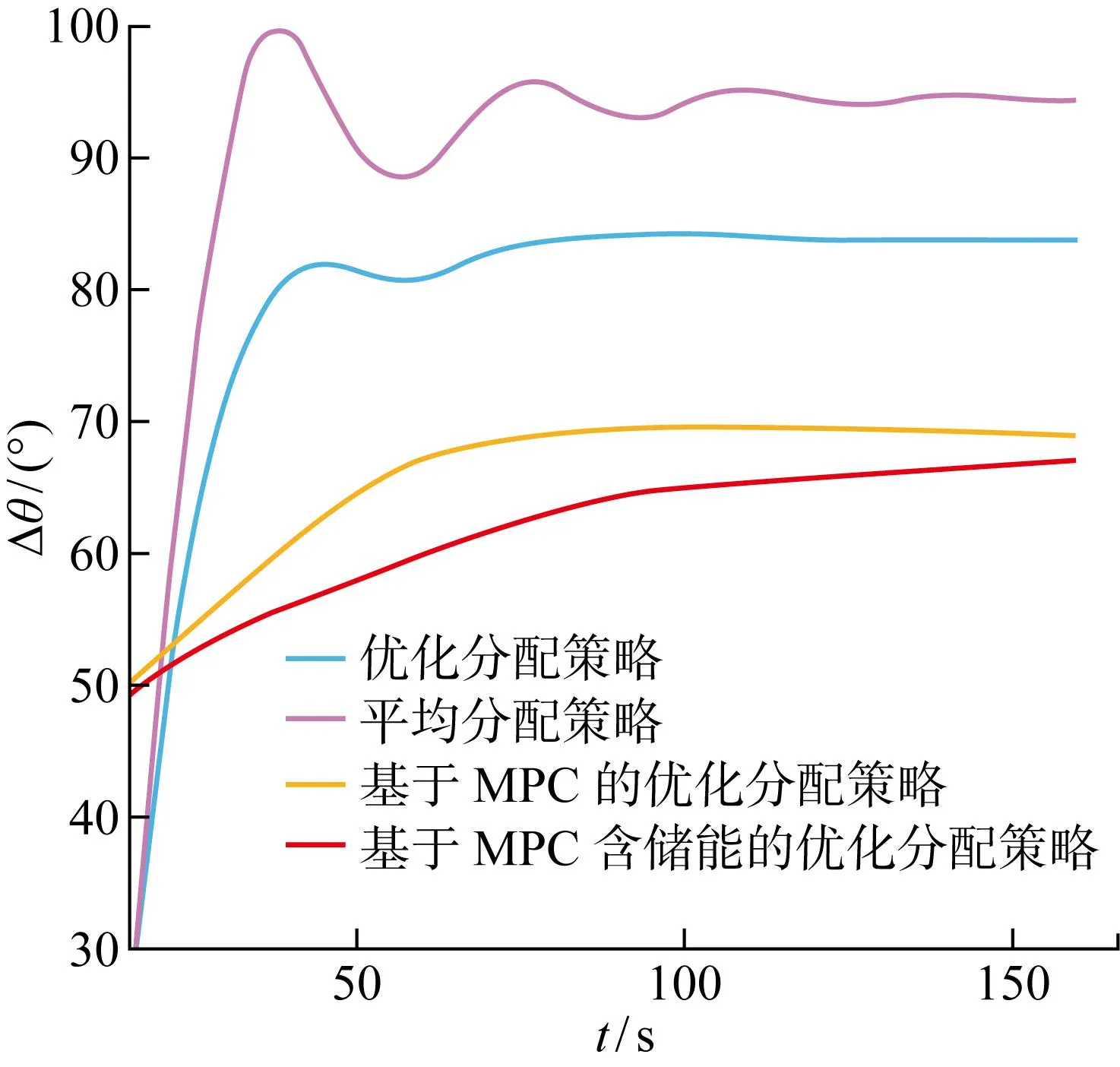
圖15 四種的槳距角變化量
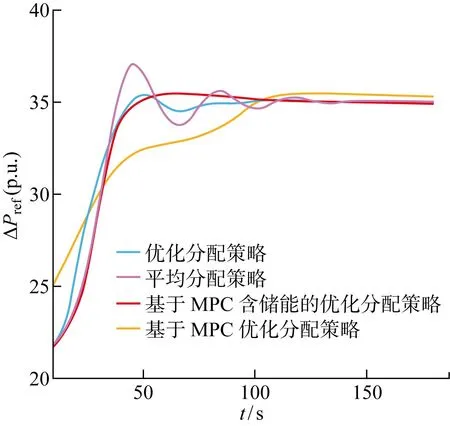
圖16 四種策略有功功率追蹤結果
5 結語
提出一種基于MPC的風儲聯合電場參與二次調頻控制策略,利用風力發電機可控的二次調頻能力和儲能系統快速響應、精確跟蹤的特性,優化風電場內儲能系統以及各風力發電機的有功分配.仿真結果表明,與傳統有功功率參考值平均分配策略和一步優化分配策略相比,本文基于MPC含儲能的槳距角優化策略可以更好地追蹤上級系統下達的有功功率指令值,避免風力發電機的槳距角過度變化,實現最小化風能損失的目標,更好實現風儲聯合電場完成二次調頻的任務.

