直動式機電運動裝置的改進磁路-運動耦合模型及快速仿真

江 鵬, 關振群, 趙國忠, 張 群, 秦志強

(1.大連理工大學 工程力學系,遼寧 大連 116024; 2.英特工程仿真技術(大連)有限公司,遼寧 大連 116023; 3.大連工業大學 藝術與信息工程學院,遼寧 大連 116400)

有限元方法和等效磁路方法已被廣泛用作電磁系統優化設計的工具[1].有限元方法具有計算精度高、適用于復雜幾何結構和非線性問題的優點,但是在計算較大規模的問題時,求解效率較低,往往不能適應機電裝置動態性能的快速評估和優化設計的需求[2-5].等效磁路方法[6-12]通過集總參數將復雜的系統簡化為簡單的數學模型,具有求解速度快、易于實現的優點,但它可能缺乏準確性,難以應用于一些具有復雜幾何形狀的模型,無法給出磁場的具體分布,常常局限于近似分析中.磁阻網絡法[13-18]是在等效磁路模塊基礎上發展而來適用于電磁機構分析和優化的方法,該方法保持了磁路法求解速度的優勢,但是為了準確計算漏磁需要建立較復雜的磁阻網絡模型[19].

等效磁路法和有限元法具有優勢互補的特點,因此空間映射技術綜合了磁路法和有限元法的優點,通過建立磁路模型與有限元模型間的映射關系,實現模型的快速計算[20-23].翟國富等[2]將空間映射方法首先應用在繼電器上,通過有限元模型數據修正磁路法的結果,在保證計算精度的同時提高了計算效率,并采用遺傳算法對電磁繼電器的動態特性進行優化.Yang等[24]在此基礎上針對繼電器設計提出一種基于補償矩陣的快速算法,該方法使用二維補償矩陣,對不同銜鐵位移、線圈電流下磁路法計算忽略的漏磁和飽和進行修正,具有計算速度快和精度高的特點.

文獻[2,24]中基于空間映射原理的電器快速仿真算法具有較廣泛的通用性,有效綜合了磁路法和有限元法的各自優勢,可以應用于一般電器產品的快速計算和優化設計.但是對于固定幾何結構、未磁飽和的電磁閥和繼電器等電器,還可以通過改進磁路模型的磁阻假設,在大幅減少有限元數值仿真次數的同時,獲得高精度的非飽和磁路模型,從而實現高效、準確的電器產品仿真計算.常規等效磁路模型常對鐵芯和氣隙的磁阻采用理想假設,雖然能解釋機電運動機構所受到的磁吸附效應,但是難以準確預測實際的仿真結果.本文在磁路模型中采用機構運動位移的3次多項式表示總磁阻,并通過上、下運動極限處的靜態磁力和電感值標定4個待定系數;改進的磁路模型可更加準確地預測磁吸力和電感隨機構運動位移的變化,進而聯合機電裝置的機構運動方程,實現電磁制動器、電磁閥等機電運動裝置的準確快速動態仿真.

1 直動式機電運動裝置的磁路-運動耦合模型

圖1所示為單邊勵磁的直動式機電運動裝置簡化模型[25],包含了機電系統的基本元件,即外端電系統、機電能量轉換系統和外端機械系統.在該模型中,外端電系統由電壓源U和電阻R串聯而成,該電阻R包括機電能量轉換系統自身電損耗在內的所有電損耗,如電壓源的等效電阻、機電能量轉換系統的繞組電阻等;e為電端口處的電壓即線圈感應電勢.設機械系統的機構運動位移x范圍為x1≤x≤x2,其中x1和x2分別為運動位移上、下極限.在機電能量轉換系統中,常設有氣隙結構,能量通過氣隙的開合實現轉換.

考慮機電裝置中的電磁-運動耦合問題,該機電裝置中的電路方程[25]為

(1)

式中:λ為磁鏈;i為線圈電流;Lw為線圈自感;t為時間.該機電裝置中的機械系統簡化為一個勁度系數為K的彈簧和一個質量為M的質量塊,所受到的磁力為Fm,則機械系統的動力方程[25]為

(2)

式中:x0為彈簧在自然松弛狀態下的x值.引入速度變量v,將電磁運動耦合系統的微分方程式(1)和(2)表示為積分形式[25],得到:

(3)

根據式(3),對于任意輸入電壓U,可以求解出結構運動位移x和線圈電流i等.

2 多項式表示總磁阻的改進模型

在直動式機電運動裝置模型中,參照文獻[25],線圈自感Lw和機構所受磁力Fm可表示為

(4)

式中:N為線圈匝數;Rt(x)為非飽和磁路的總磁阻;Rc(x)為鐵芯磁阻;Rg(x)為氣隙磁阻.當機構運動位移x變化時,運動氣隙邊緣及相鄰鐵芯端部的磁場變化一般較為復雜,Rc(x)往往不是常值,Rg(x)與氣隙厚度或運動位移x也不滿足簡單的線性關系.為了更加準確地預測Fm和Lw隨x的變化規律,對Rt(x)采用x的n次多項式表示為

Rt(x)=(A+Bx+Cx2+Dx3+…)ν0

(5)

式中:A、B、C和D等為多項式的待定系數,其中A為機構初始狀態(運動位移為0)時的磁阻,Bx為磁阻的線性變化部分,Cx2+Dx3+…表示運動位移引起磁阻變化的高階量;ν0為空氣磁阻率常數,作為多項式的比例因子.將圖2(a)中分布的鐵芯磁阻和氣隙磁阻集中為式(5)中多項式表示的總磁阻Rt(x),得到圖2(b)的磁路模型.

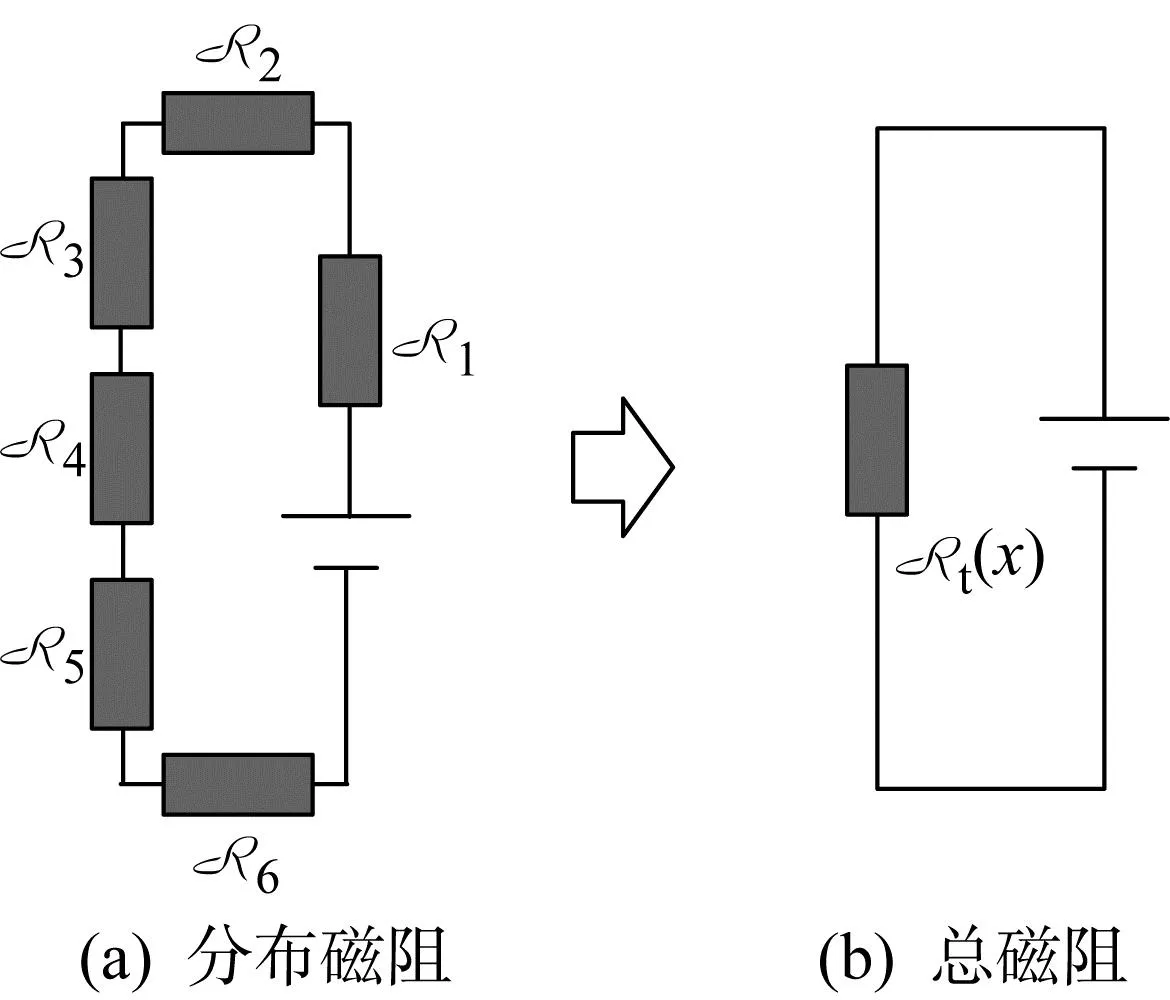
圖2 直動式機電裝置的磁路模型

由式(4)和總磁阻表達式(5),Lw和Fm可以進一步表示為

(6)

(7)

由式(6)和式(7)可知,可利用不同位移x處的線圈電感Lw或機構所受磁力Fm的仿真值標定系數A、B、C、D等.雖然式(5)中多項式的階次越高,對總磁阻的擬合精度也越高,但是過高的階次對改善精度的作用較小,同時,過多的待定系數需要較多的數值仿真進行標定.本文限定式(7)中的多項式階次n≤3,且僅利用直動式機構在運動上、下極限處的靜態線圈電感和磁吸力的仿真值標定待定系數.Lw(x1)和Fm(x1)是對應x1的電感和磁力數值仿真解,分別簡記為L1、F1;Lw(x2)和Fm(x2)是對應x2的電感和磁力數值仿真解,分別簡記為L2、F2.

當選擇多項式次數n=1時,式(5)中的總磁阻是機構運動位移x的1次多項式:

Rt(x)=(A+Bx)ν0

(8)

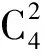
當選擇多項式次數n=2時,總磁阻是機構運動位移x的2次多項式:

Rt(x)=(A+Bx+Cx2)ν0

(9)

當選擇多項式次數n=3時,總磁阻是機構運動位移x的3次多項式:

Rt(x)=(A+Bx+Cx2+Dx3)ν0

(10)

由于可利用的標定值有4個,所以僅有1種標定方式,需要利用全部L1、F1、L2、F2來標定系數:

(11)

相比1次和2次多項式磁阻模型,3次多項式磁阻模型可以表示機構運動引起的更復雜的磁阻變化,同時3次多項式磁阻模型充分利用上、下運動位移極限處的靜態線圈電感和磁力仿真值標定未知系數,因而一般具有更高的精度.

3 基于改進3次磁路-運動耦合模型的快速仿真

非飽和磁阻多項式的系數由靜態線圈電感和機構所受磁力確定,可適用于直動式機電運動裝置不同運行工況的動態分析.將式(10)中改進的磁阻Rt(x)代入式(6)可得到改進的電感Lw(x)和電感梯度dLw(x)/dx,進一步代入式(3),可得到改進的磁路-運動耦合模型.基于改進的3次磁路-運動耦合模型仿真流程如圖3(a)所示,主要包括以下幾個步驟:首先,采用數值仿真手段獲得運動位移上極限處x1的磁力F1和電感L1,以及運動位移下極限處x2的磁力F2和電感L1;然后,利用兩個運動極限處的磁力和電感仿真值,根據式(11)計算式(10)中的系數A、B、C和D,從而確定Lw(x)和dLw(x)/dx的表達式;最后,通過搭建的Simulink系統計算動態特性方程(3),并繪制i和x等變量的時間歷程曲線.圖3(b)為動態特性方程(3)在Simulink系統中的實現,圖中的3個積分器分別對應式(3)中的3個積分方程.

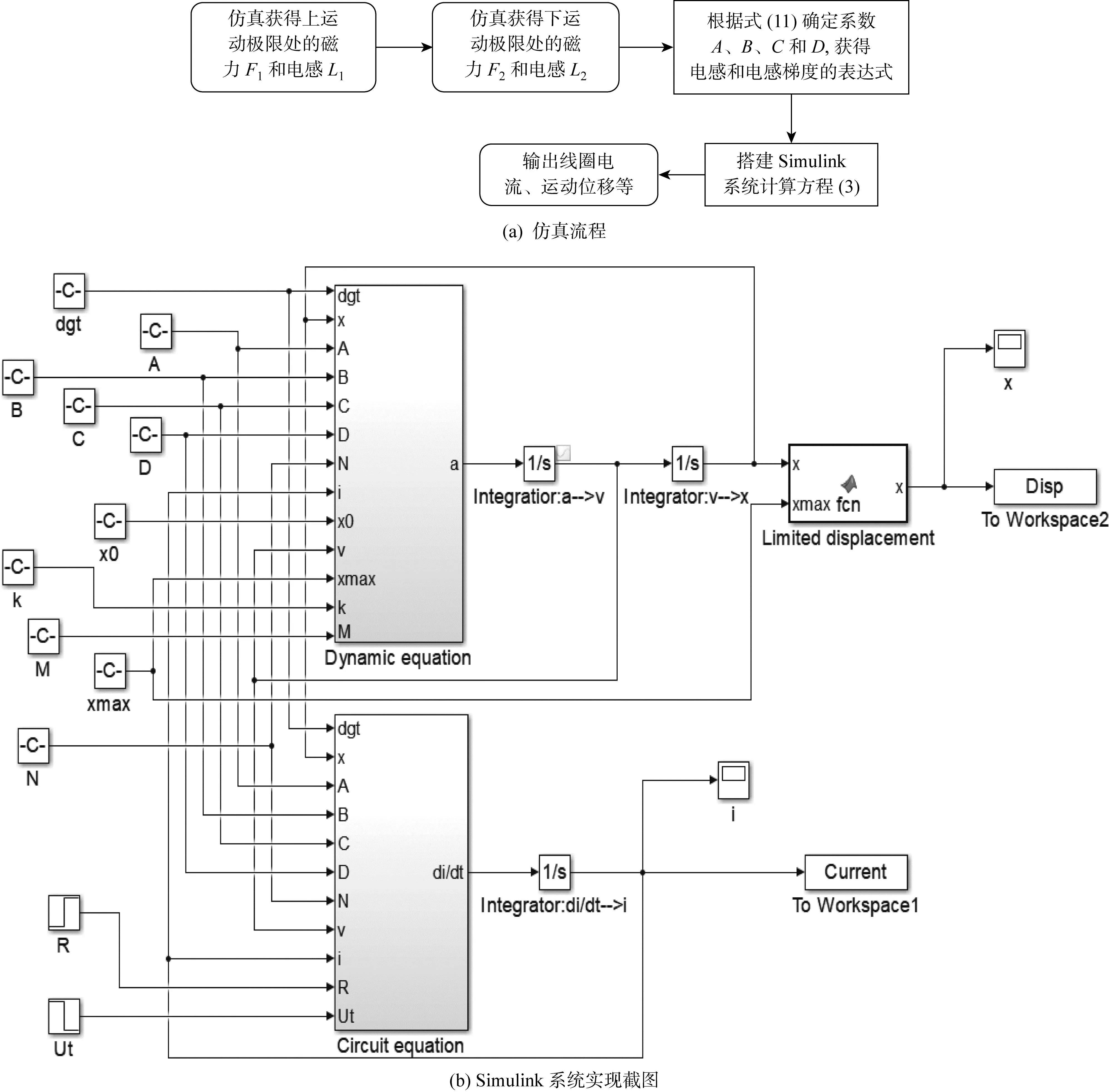
圖3 基于改進磁路-運動耦合模型的快速動態仿真流程

4 算例驗證

4.1 電磁制動器動態特性的快速仿真

圖4所示為制動器主體的軸對稱幾何模型和外電路.在圖4(a)的主體結構中,上端運動銜鐵與彈簧相連,銜鐵下方為靜止的護鐵.定義銜鐵向上運動為正方向,當銜鐵與護鐵接觸時位移為0,并限定銜鐵的運動上、下極限位移分別為0.5和2.5 mm,銜鐵初始位移為2.5 mm.在圖4(b)的電路模型中,絞線圈作為電路中的一部分,與24 V的電源及開關構成回路,并與續流電阻和二極管并聯,續流電阻Rf為100 Ω.絞線圈匝數N為2 548,線圈電阻Rw為50 Ω,銜鐵和護鐵的相對磁導率分別設為 2 000 和 1 000,銜鐵質量M為0.25 kg,彈簧勁度系數K為1 kN/m,初始拉伸長度為0.01 m.仿真總時長為0.2 s,開始時電源開關閉合,在0.1 s時斷開.

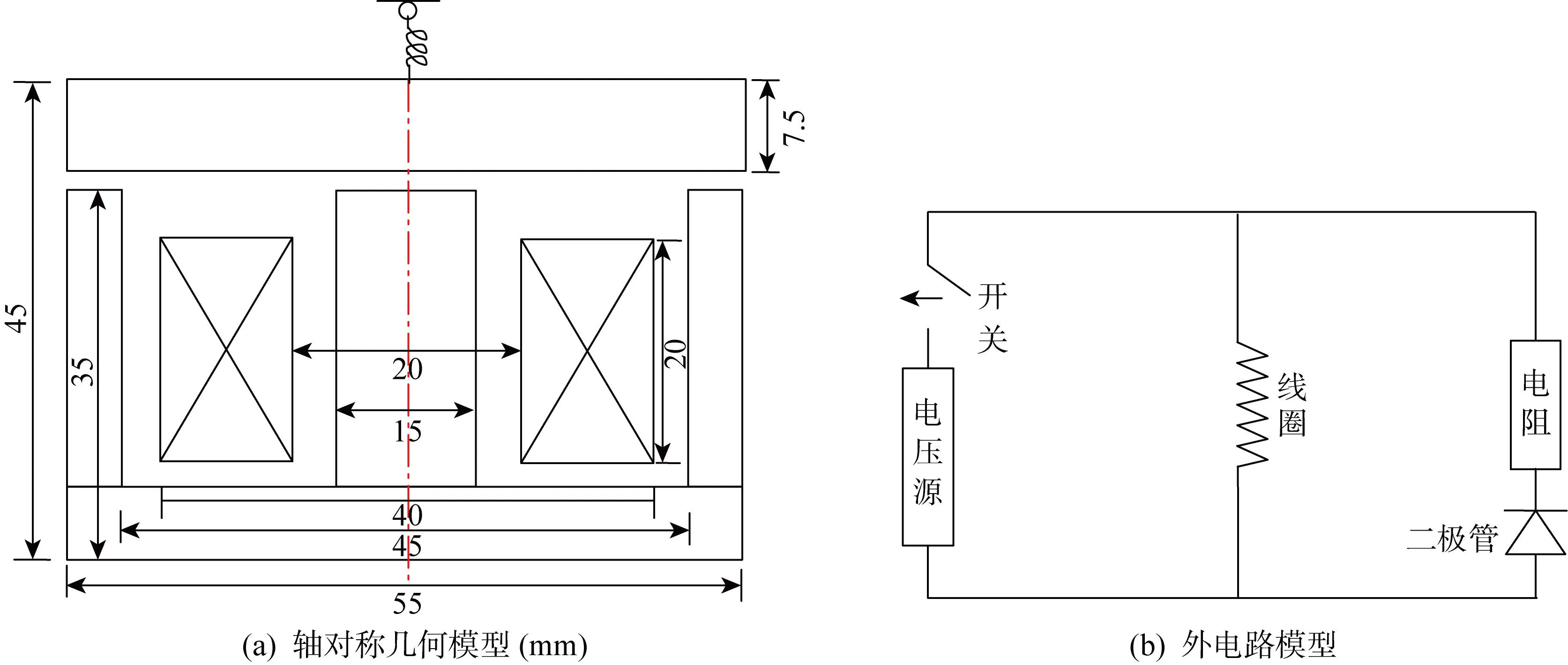
圖4 電磁制動器軸對稱幾何模型和外電路模型

在對該電磁制動器進行動態仿真前,對比數值模型和不同磁路模型計算得到的磁力和電感隨氣隙厚度變化曲線,驗證改進的3次磁路模型具有較高的精度.設定線圈穩態電流大小為0.48 A,利用上、下運動極限處靜態電感和磁力的數值仿真結果標定不同階次總磁阻磁路模型的待定系數,得到表1中的待定系數值.圖5對比了理想磁路模型、改進的磁路模型以及有限元模型計算得到的磁吸力和電感隨氣隙厚度或運動位移的變化曲線.其中有限元模型采用三角形網格劃分,網格總數為 3 708,當銜鐵運動時,氣隙網格會發生擠壓變形.可以發現,改進的3次磁路模型具有最高的精度,準確地預測了不同氣隙厚度的磁力和電感的有限元仿真結果,說明3次多項式表示的總磁阻磁路模型充分考慮了氣隙厚度變化引起的氣隙邊緣及鐵芯端部磁場變化.

表1 電磁制動器磁路模型系數值

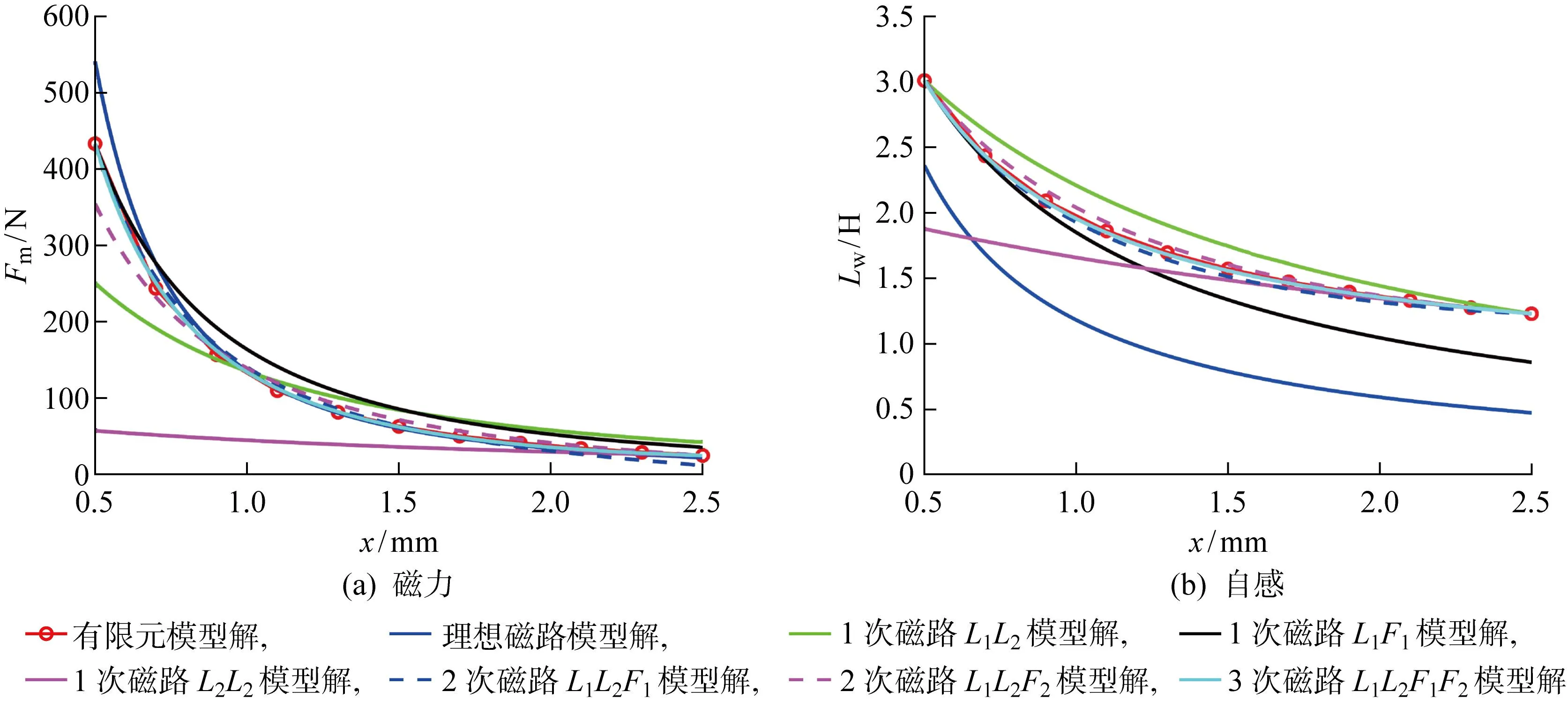
圖5 電磁制動器中磁力與自感對比

利用不同階次的磁路-運動耦合模型,在Simulink系統中對該電磁制動器的動態過程進行仿真.圖6為線圈電流、線圈感應電勢e、銜鐵磁力及運動位移的時間歷程曲線,并且與有限元-運動耦合模型的仿真結果進行對比,發現只有改進的3次磁路-運動耦合模型能夠準確預測該制動器動態過程的各個輸出量.此外,改進的3次磁路-運動耦合模型將有限元仿真所需的223 s縮短為1.6 s,大幅提高了電磁制動器動態特性計算的效率.

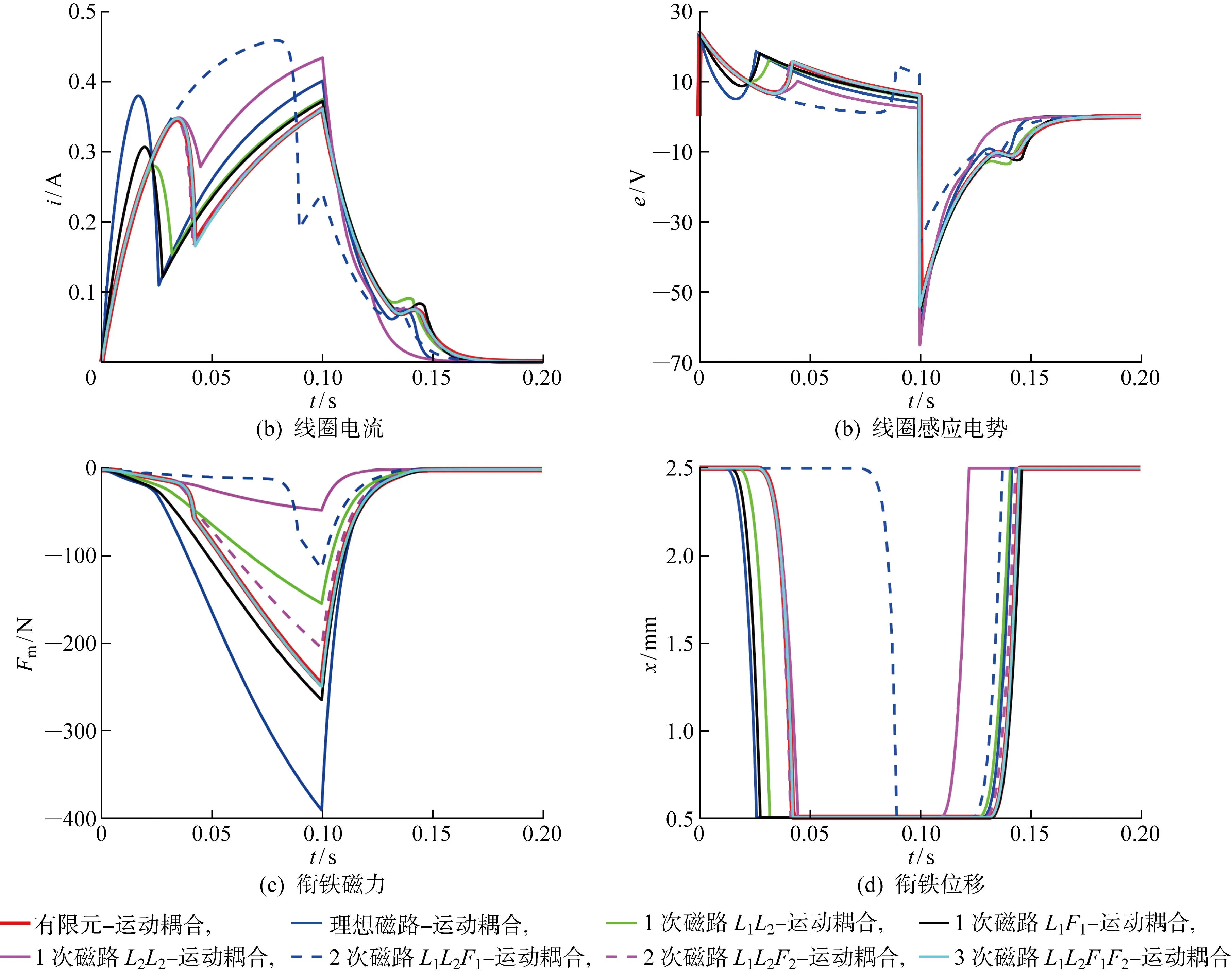
圖6 電磁制動器中改進的磁路-運動耦合模型與有限元-運動耦合模型的結果對比

4.2 伺服閥動態特性的快速仿真

圖7為某伺服電磁閥的軸對稱幾何模型示意圖.鐵芯材料的相對磁導率為 4 000,Rw為55 Ω.電磁閥外電路采用圖4(b)中的電路模型,Rf為 100 Ω.在初始時刻打開開關,然后在0.05 s閉合開關,因此在0.05 s時,式(3)中的電壓U從初始24 V變為0,電路總電阻R從55 Ω變為150 Ω.

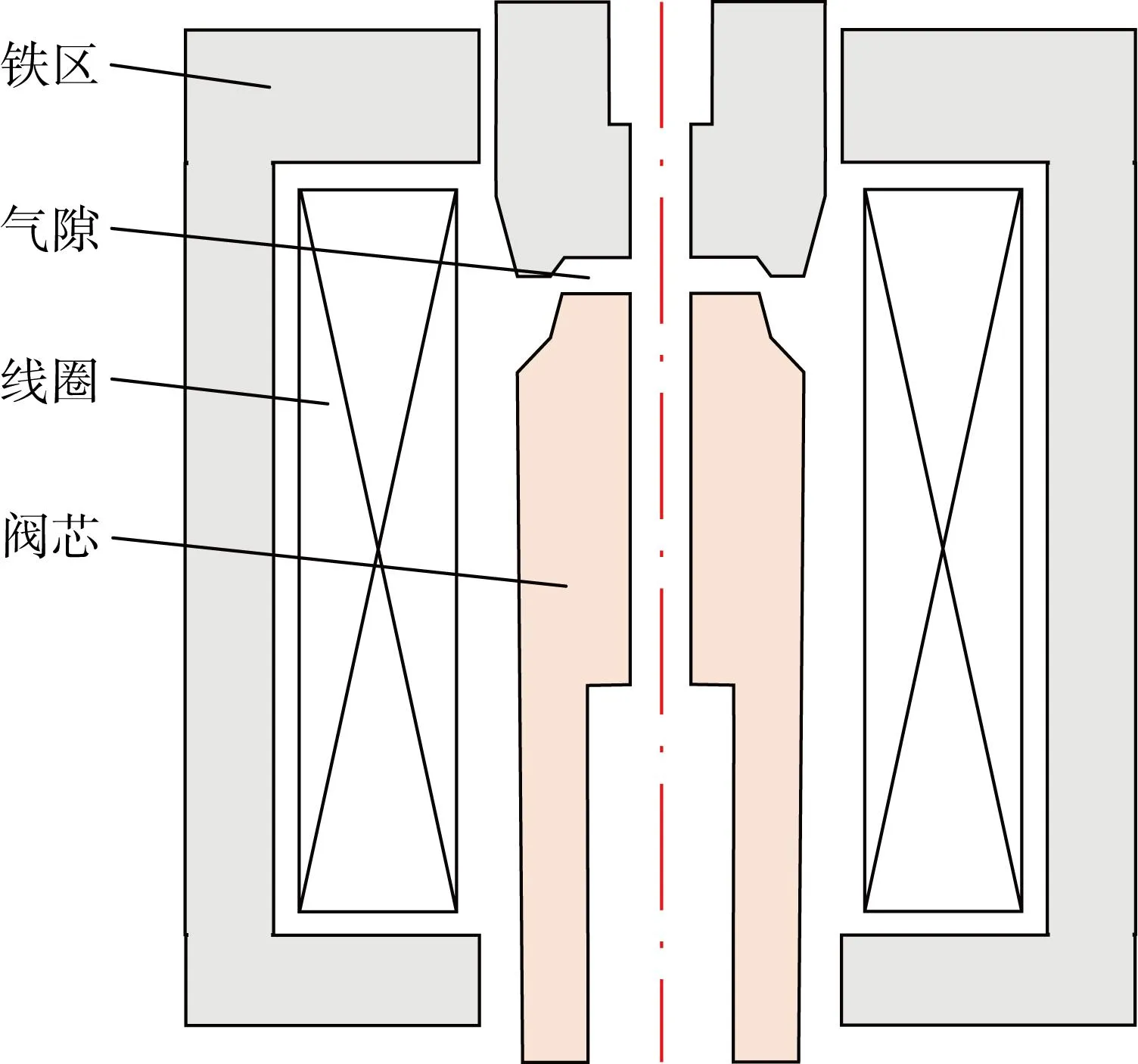
圖7 電磁比例閥軸對稱幾何模型示意圖

利用改進的3次磁路-運動耦合模型對電磁比例閥進行快速動態仿真.首先,通過將上、下運動極限處電磁閥的靜態電感和閥芯所受磁力的有限元仿真結果代入式(11),確定式(10)中總磁阻3次多項式的4個系數,得到電感和電感梯度表達式,從而確定動態特性方程(3);然后,對方程(3)采用圖3(b)中搭建的Simulink系統進行快速求解,得到圖8中線圈電流、線圈感應電勢、閥芯磁力及位移的計算結果.有限元-運動耦合模型采用三角形網格劃分,網格總數為12 284,當銜鐵運動時,采用氣隙動網格技術求解.通過與有限元-運動耦合模型的計算結果對比,可以發現兩者結果曲線較吻合,說明改進的磁路-運動耦合模型可以準確反映有限元仿真結果;此外,改進的磁路-運動耦合模型將有限元仿真所需的626 s縮短僅為1.5 s,大幅提高了電磁比例閥動態特性計算的效率.

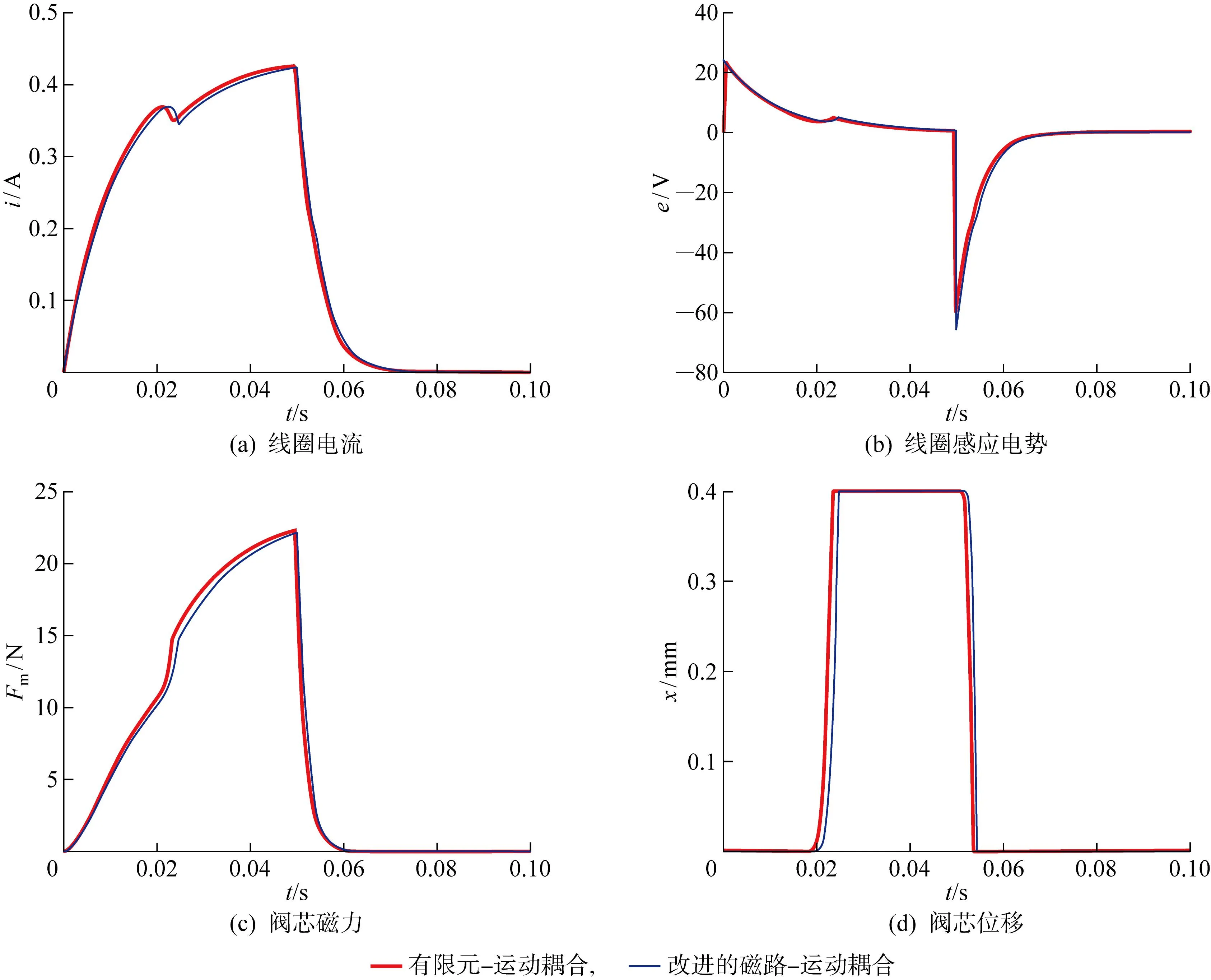
圖8 電磁比例閥中改進的磁路-運動耦合模型與有限元-運動耦合模型的結果對比

改進的3次磁路-運動耦合模型與有限元-運動耦合模型并非完全吻合,這主要由于:一方面磁路模型采用3次多項式描述總磁阻,仍然存在一定擬合誤差;另一方面改進的3次磁路-運動模型與有限元-運動模型采用了不同的時間離散方案,其中有限元-運動耦合模型中的電磁場模型采用一階向后Euler法,而改進的3次磁路-運動耦合模型采用Simulink自帶的4階Runge-Kutta法.

5 結語

對未磁飽和的直動式機電運動裝置提出一種改進的磁路-運動耦合模型,該模型對非飽和磁路總磁阻采用機構運動位移的3次多項式描述,可更加準確地反映磁力和電感隨機構運動位移變化的規律.該模型無需定義鐵芯部件和氣隙的等效長度和橫截面積等,利用機構運動極限處電感和磁力有限元仿真結果或實測值確定總磁阻的3次多項式系數.所得到的改進磁路-運動耦合模型在保證計算精度的同時,實現未磁飽和直動式機電運動裝置的秒級快速動態仿真,可有效替代計算耗時的有限元-運動耦合仿真.