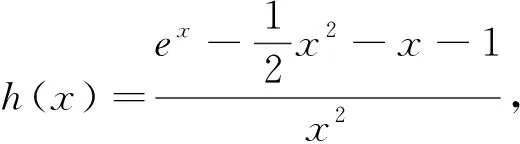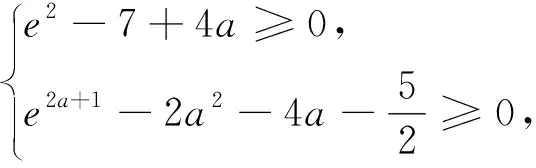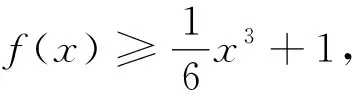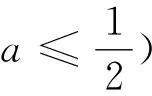端點效應(yīng)不靈了?
黃永生 紀(jì)建靈
福建省泉州市第七中學(xué) (362000);福建師范大學(xué)泉州附屬中學(xué) (362000)
2020年全國一卷理科21題第(2)小題為不等式恒成立求參數(shù)范圍問題,具有高度的迷惑性,考生解題時很容易陷入“端點效應(yīng)”的誤區(qū).本文從“端點效應(yīng)”典例出發(fā),探究誤用“端點效應(yīng)”產(chǎn)生錯解的根本原因,并提出“端點效應(yīng)”模型的四種判斷策略,從而提升解題效率.
1 端點效應(yīng)及應(yīng)用典例
定義在[a,+∞)上的函數(shù)f(x),若滿足f(a)=0,f′(a)=f″(a)=…=f(n-1)(a)=0,f(n)(a)≥0且f(n)(x)單調(diào)遞增,則f(x)≥0在[a,+∞)恒成立.
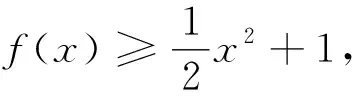
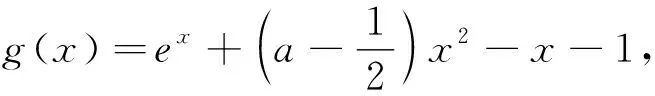


(2)當(dāng)g″(0)=2a<0,即a<0時,由g″(x)=ex+2a-1=0得x=ln(1-2a).
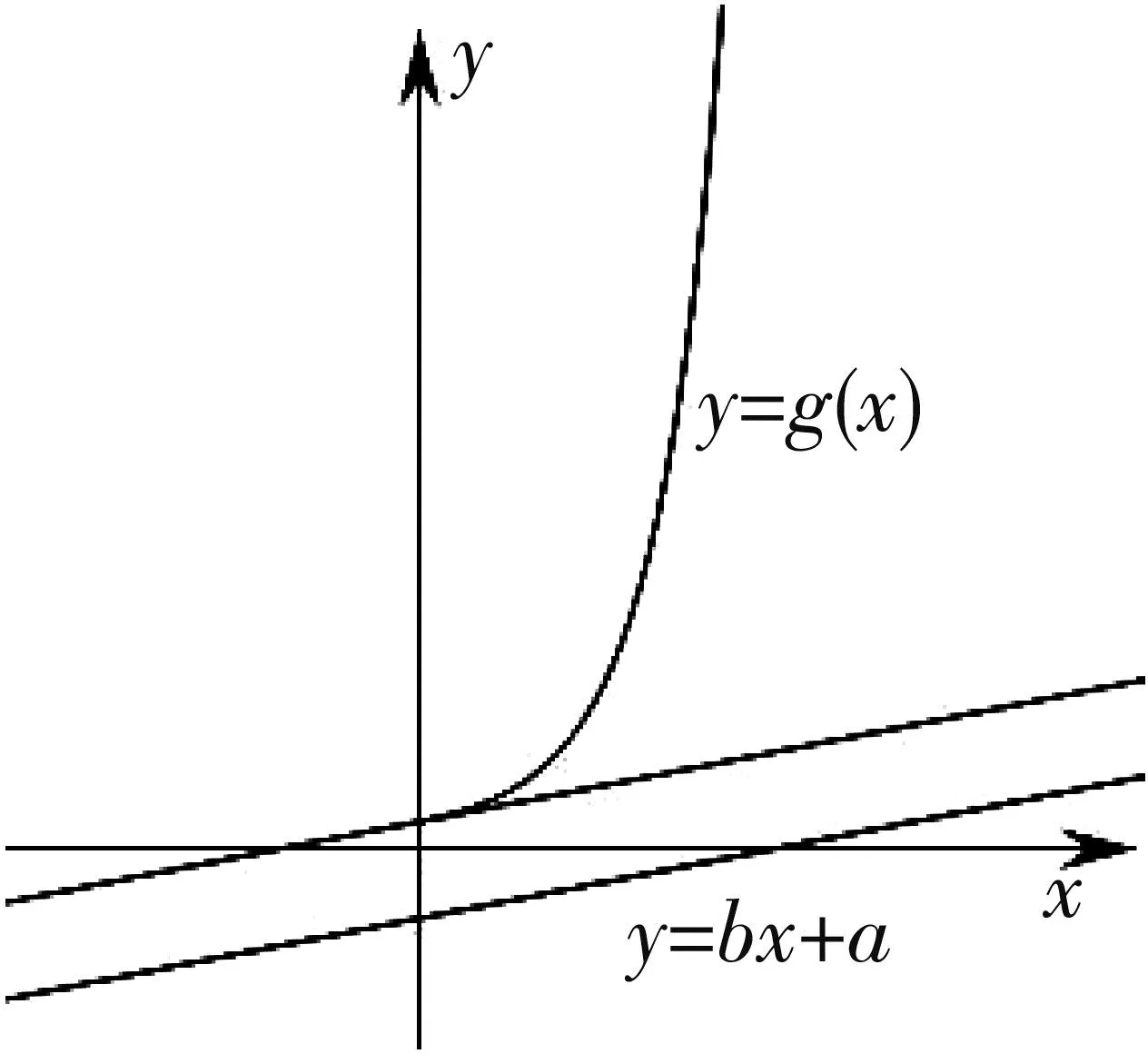
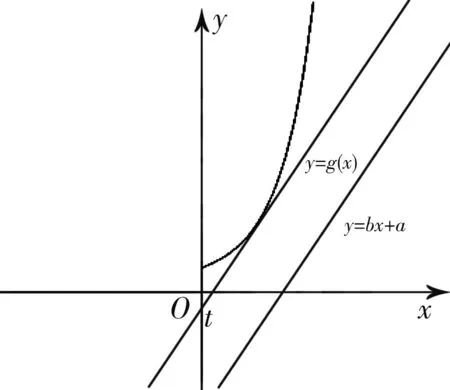
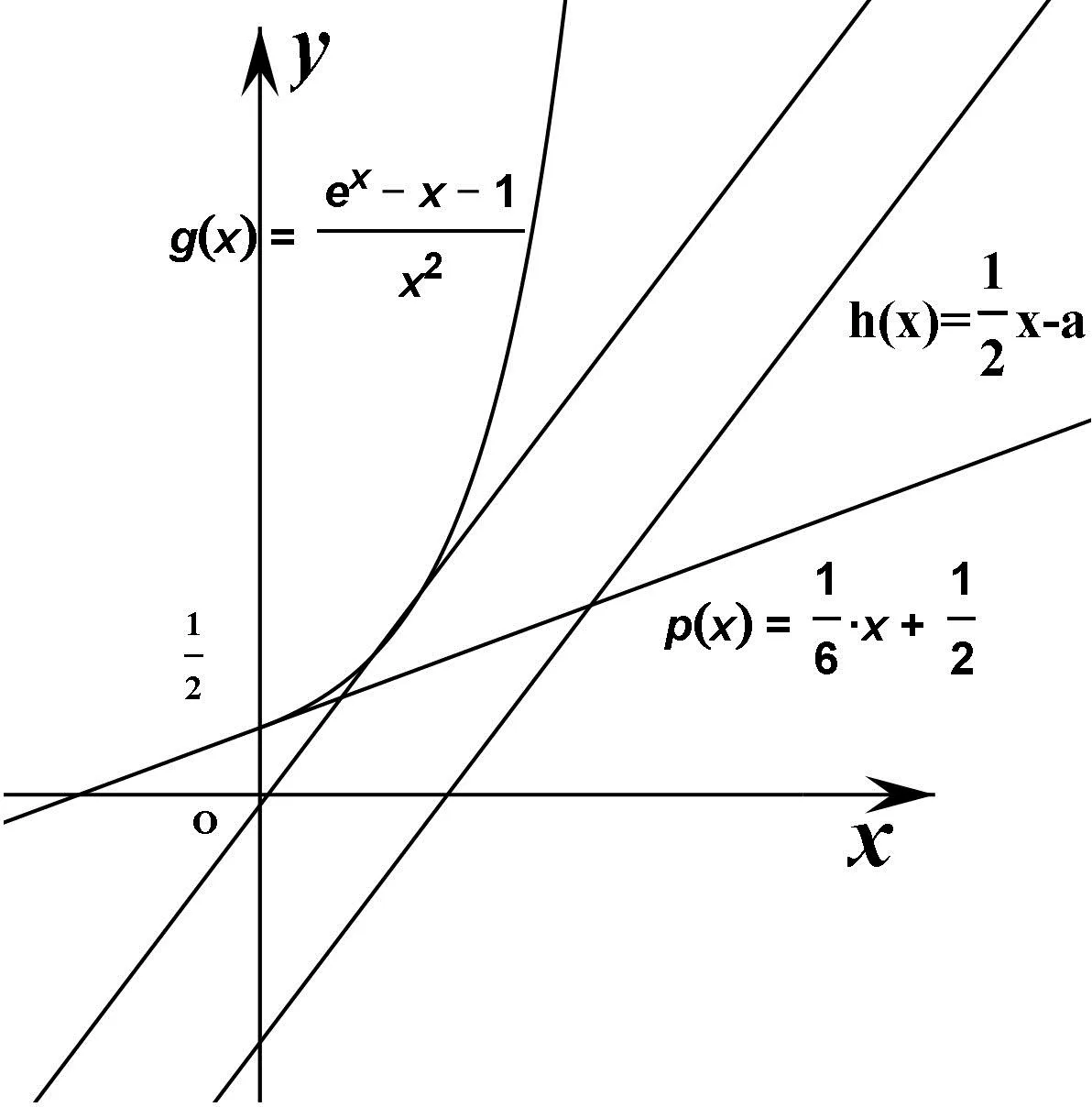
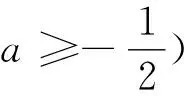
當(dāng)x∈(0,ln(1-2a))時,g″(x)<0,g'(x)單調(diào)遞減.所以g'(x) 綜上,a≥0. 評析:端點效應(yīng)試題的結(jié)構(gòu)為“若x∈[a,+∞),f(x,m)≥0,求m的取值范圍”,其解題思路為:①觀察得f(a)=0,由f'(a)≥0得到一個必要條件;若f'(a)=0恒成立,則由f″(a)≥0得到必要一個條件;若f″(a)=0恒成立,則重復(fù)以上步驟,得到m∈P.②證明m∈P,f(x,m)≥0成立;③當(dāng)m?P時,找到區(qū)間,證明f(x,m)<0. 圖1 策略1f(n)(x)的正負(fù)性與單調(diào)性 定義在[a,+∞)上的函數(shù)f(x),若滿足f(a)=0,f'(a)=f″(a)=…=f(n-1)(a)=0,f(n)(a)≥0且f(n)(x)單調(diào)遞增,則f(x)≥0在[a,+∞)上恒成立. 策略2泰勒展開式 策略3數(shù)形結(jié)合 設(shè)g(x)為下凸函數(shù),不等式g(x)≥bx+a對于任意x∈(0,+∞)恒成立.即要找到最佳系數(shù)a,b使直線y=bx+a恒在曲線y=g(x)的下方.考慮直線y=bx+a與曲線y=g(x)相切為臨界狀態(tài).直觀發(fā)現(xiàn):如圖2,當(dāng)切點在端點,即b=g'(0),則a≤g(0);如圖3,當(dāng)切點不在端點,即b>g'(0),則a≤t.(t為相切時切線在y軸的截距) 圖2 圖3 顯然,圖2為端點效應(yīng)問題,圖3為非端點效應(yīng)問題. 圖4 策略4尋找最值點 基于策略3的討論,例2可改編為以下試題,有興趣的讀者不妨運用以上策略判斷是否為端點效應(yīng)問題,再作解答. 試題1 已知函數(shù)f(x)=ex+ax2-x.當(dāng)x≥0時,f(x)≥(3-e)x3+1,求a的取值范圍. (答案:a≥5-2e) 試題3 已知函數(shù)f(x)=ex+sinx,當(dāng)x≥0時,f(x)≥ax2+2x+1,求a的取值范圍.2 誤用端點效應(yīng)及錯因分析

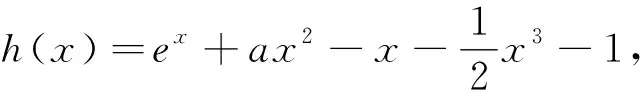

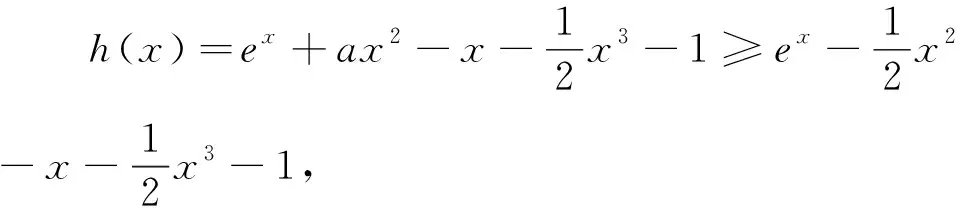
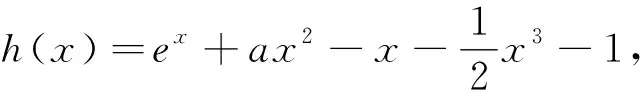
3 端點效應(yīng)的判斷策略