運用方程思想解決幾何問題“六法”
? 江蘇省蘇州相城區陽澄湖中學 王偉星
運用方程思想解決幾何題,是把一些看上去與方程沒有明顯聯系的幾何問題,運用方程的思想巧妙地轉化為方程(組),通過解方程(組)最終使問題獲解.這種方法不僅直觀,容易找到解題思路,而且能夠避免繁瑣的計算與復雜的推理,大大簡化了解題過程,具有極大的優越性.
1 代入面積
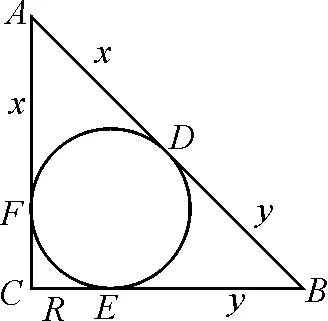
圖1
例1在△ABC中,∠C=90°,⊙O為它的內切圓,與邊AB,BC,CA分別切于點D,E,F.
求證:S△ABC=AD·BD.
證明:如圖1,設AD=x,BD=y,⊙O的半徑為R,則
在Rt△ACB中,由勾股定理,可得
(x+R)2+(y+R)2=(x+y)2.
化簡,得xy=R(x+y)+R2.
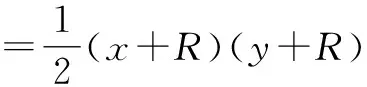
故S△ABC=AD·BD.
方法與技巧:先對切線、圓半徑設元,目的是建立三角形的邊、高與切線之間的聯系,再通過勾股定理變形,最后代入三角形的面積公式,證明過程充分體現了方程思想的靈活應用.
2 設元轉換
例2如圖2,已知AC切⊙O于點C,CP為⊙O的直徑,AB切⊙O于點D與CP的延長線交于點B,若AC=PC.求證:(1)BD=2BP;(2)PC=3BP.
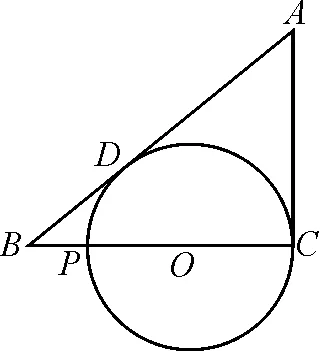
圖2
證明:(1) 如圖3,連接DO.
因為AC,AB分別切⊙O于點C,D,AC=PC,設PO=OC=DO=x,所以AC=PC=AD=2x.
因為OD⊥AB于點D,AC⊥BC于點C,所以可得△BOD∽△BAC.
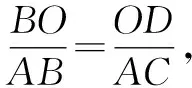
化簡,得BD=2BP.
(2)在Rt△BOD中,由勾股定理,可得OB2=OD2+BD2,即(BP+x)2=x2+(2BP)2.
化簡,得2x=3BP,即PC=3BP.
方法與技巧:本題的證明運用了“設元轉換”的方程思想.第(1)問通過證明三角形相似,利用相似比證得BD=2BP;第(2)問運用勾股定理,通過逐步化簡推得PC=2BP.
3 尋找相等關系
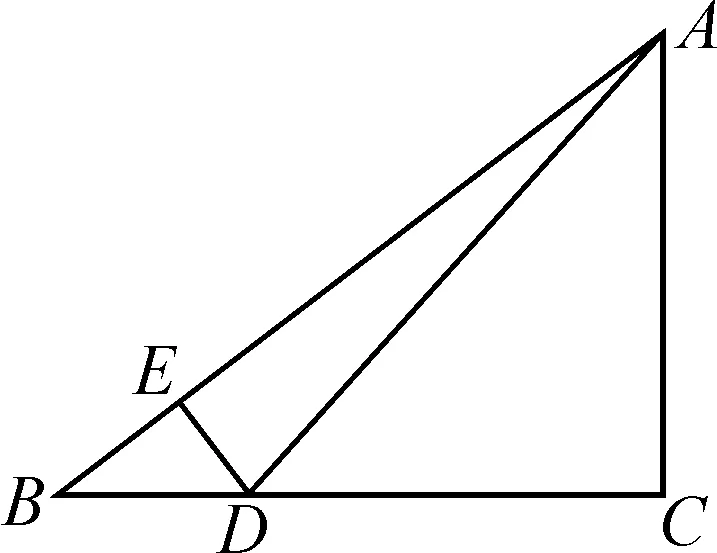
圖4
例3如圖4,在△ABC中,∠C=90°,D是BC邊上一點,DE⊥AB于點E,∠ADC=45°.若DE∶AE=1∶5,BE=3,求△ABD的面積.
解:因為DE∶AE=1∶5,所以設DE=k,則AE=5k.
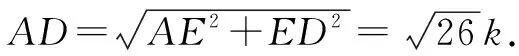
因為在△ADC中,∠C=90°,∠ADC=45°,所以
在Rt△BED中,BE=3,所以
因為∠B=∠B,∠BED=∠C=90°,所以可得△BED∽△BCA.
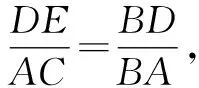
整理,得2k2+5k-18=0.
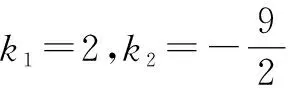
所以k=2.
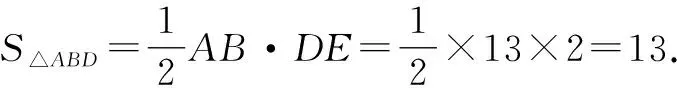
方法與技巧:本題的技巧主要體現在如何尋找相等關系上.要求△ABD的面積,只要求出DE與AB的長即可.由已知DE∶AE=1∶5,設DE=k,可得AE=5k,再由已知可得△BED∽△BCA,然后利用DE∶AC=BD∶BA的相等關系,即可列出關于k的一元二次方程.
4 轉設方程組
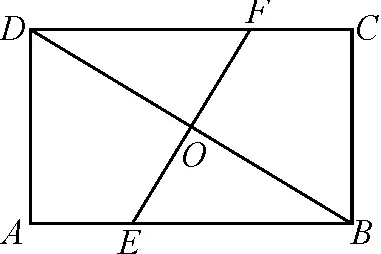
圖5
例4如圖5,在矩形ABCD中,EF是BD的垂直平分線,已知BD=20,EF=15,求矩形ABCD的周長.
解:設矩形的長AB=x,寬BC=y.在Rt△BAD中,BD2=AD2+AB2,即x2+y2=202.因為EF是BD的垂直平分線,則有BO=OD=10,所以△OFD≌△OEB.所以OE=OF=7.5.因為∠EBO=∠DBA,∠A=∠EOB=90°,所以△EOB∽△DAB.所以AB∶AD=OB∶OE,即x∶y=10∶7.5.
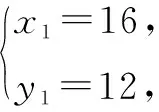
所以,矩形的周長為2(16+12)=56.
方法與技巧:要求矩形ABCD的周長,必須要知道它的長和寬.不妨設長為x,寬為y,由于未知數有兩個,因此要找到兩個等量關系列出兩個方程.可由勾股定理和相似三角形的性質定理得到關于x,y的兩個方程,解這個方程組即可獲解.
5 活用余弦定理
例5設P是定角∠MAN的平分線上一定點.過A,P兩點任作一圓,與∠MAN的兩邊分別交于B,C兩點.求證:AB+AC為定值.
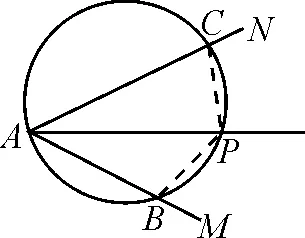
圖6
證明:如圖6,設∠CAP=∠BAP=α,AP=a,由余弦定理,得PB2=AP2+AB2-2AB·APcosα,即
AB2-2acosα·AB+a2-PB2=0.
同理,可得
AC2-2acosα·AC+a2-PC2=0.
因為PC=PB,由上述兩個方程可知,AB,AC為一元二次方程x2-2acosα·x+a2-PB2=0的兩根.由韋達定理,可知AB+AC=2acosα(定值).
方法與技巧:本題的證明技巧表現在靈活運用余弦定理,“溝通”了AB,AC與a,α之間的關系,先討論特殊情況,再探求一般情況,最后結合韋達定理使問題得證.
6 化為一元二次方程
圖7
例6如圖7,已知在Rt△ABC中,∠C=90°,AC=3,BC=4,點E在直角邊AC上(點E與A,C兩點均不重合).
(1)若點F在斜邊AB上,且EF平分Rt△ABC的周長,設AE=x,試用含x的代數式表示S△AEF.
(2)若點F在折線ABC上移動,試問:是否存在直線EF將Rt△ABC的周長和面積同時平分?若存在,則求出AE的長;若不存在,請說明理由.
圖8
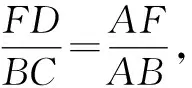
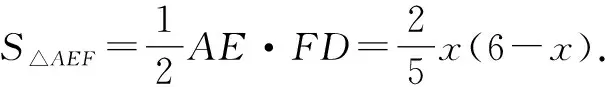
(2)假設存在直線EF將Rt△ABC的周長和面積同時平分.
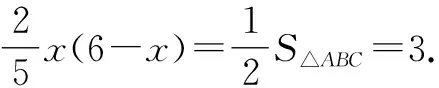
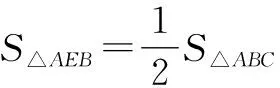

圖9
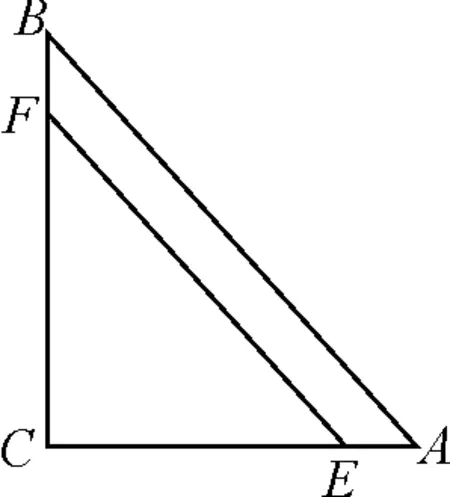
圖10
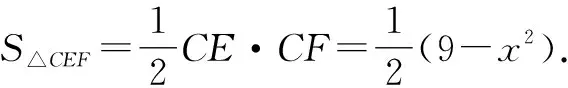
方法與技巧:本題將三角形的面積、周長、點的位置關系等問題巧妙地轉化為一元二次方程來解決.第(1)問利用了相似三角形的相似比;第(2)問根據點F的不同位置,借助圖形分為三種情況進行了討論、排除.
綜上所述,運用方程思想解決幾何問題,首先要考慮把哪個幾何量看作未知數;其次,要找出“形”與“式”之間的內在聯系,例如相等、相似關系.在幾何問題中,公理、定理、公式、性質,以及題目給出的數量關系、圖形中的某些位置關系等,都有可能為我們用方程思想解題提供依據.

