基于MⅠMO-ESO的高速飛行器自抗擾控制
樊 軼,秦昌茂,董 添,王 興
(中國運載火箭技術研究院,北京,100076)
0 引 言
高速飛行器近年來成為研究的熱點[1],無動力再入過程中具有的復雜非線性、控制通道間強耦合及氣動參數不確定性的因素增加了控制器設計的困難。目前已有的魯棒控制[2-3]、自適應控制[4-5]等方法,被控系統(tǒng)的線性化模型包含復雜的高階導數函數,不便于工程實際應用。滑模控制[6-8]通過設計虛擬控制量來補償不確定性的影響,但是滑模控制是基于不確定性的上界設計的,要求其界為已知或是為狀態(tài)變量的已知函數,這在實際應用中很難實現。
自 抗 擾 控 制 器[9](Auto Disturbance Rejection Controller,ADRC)是一種依靠過程誤差來消除誤差的方法,不依賴于系統(tǒng)模型,通過擴張狀態(tài)觀測器(Extended States Observer,ESO)估計“總和擾動”來獲得對象模型中的內擾和外擾的實時作用量,并進行實時動態(tài)反饋補償,實現系統(tǒng)的線性化,又采用了非線性反饋控制律(Nonlinear States Error Feedback Control Laws,NLSEF)來抑制補償殘差,提高控制性能[10-11]。自抗擾控制技術經過十幾年的發(fā)展,已逐步成熟,德州儀器在2013 年發(fā)布以自抗擾技術為核心的運動控制芯片,進一步證明了自抗擾技術在工程應用上的巨大潛力[12-13]。
本文基于高速飛行器無動力再入姿態(tài)非線性模型,設計了MⅠMO-ESO 自抗擾姿態(tài)控制器。將不確定項、未建模動態(tài)、耦合影響、參數攝動及干擾影響作為“總和干擾”,利用ESO 進行估計并動態(tài)反饋補償,再利用NLSEF 抑制補償殘差,依靠自抗擾不依賴模型的特點,解決了模型復雜線性化及滑模控制需要攝動界的問題。按照ESO 穩(wěn)定性條件選擇參數,可以獲得良好的動態(tài)品質和跟蹤性能,并能夠克服干擾及氣動參數大范圍攝動的影響,具有較強的魯棒性。
1 高速飛行器建模
將飛行器繞質心運動方程投影到彈體坐標系并展開得到以下方程組:
式中ωx、ωy和ωz分別為滾轉、偏航和俯仰角速度;θ為飛行器彈道傾角;α,β和γc分別為飛行器的攻角、側滑角和速度傾斜角;Ix、Iy和Iz為飛行器的主轉動慣量;m為飛行器質量,無動力再入過程中一般為常值。
X、Y和Z分別是阻力、升力和側向力。
式中ρ為大氣密度;V為飛行速度;S為飛行器的翼面參考面積;q為動壓;CX、CY和CZ分別為阻力系數、升力系數和側向力系數。
式中δe,δa,δr分別為左、右升降副翼和方向舵3 個舵面的偏轉角;l,m和n分別為滾轉力矩、偏航力矩和俯仰力矩。

上述符號中gi,j為氣動參數項,具體參數詳見文獻[15]。與一般低速飛行器不同的是,各個氣動參數項都是攻角和馬赫數的函數,并且包含氣動參數攝動引起的不確定性,增強了通道間的耦合,導致控制器設計更加復雜和困難。
2 基于MⅠMO-ESO的自抗擾控制
2.1 基于MⅠMO-ESO的自抗擾控制器設計
針對式(9),擴張狀態(tài)觀測器ESO的設計是整個自抗擾控制器的核心。每個通道均為一階系統(tǒng),因而只需重構二階擴張狀態(tài)觀測器ESO。控制量δ的輸入矩陣參數B與氣動參數相關,雖然有相關參數可參考,但是并不是精確值,故B取參考的氣動參數作為標稱值B0。由于f(x)也存在參數攝動及不確定項,因此用f(·)代替,f(·)為總的不確定項,包括f(x)及外部環(huán)境、未建模動態(tài)、耦合影響等干擾。
用估計值g0代替g(x),f(·)代替f(x),則式(9)可等效為
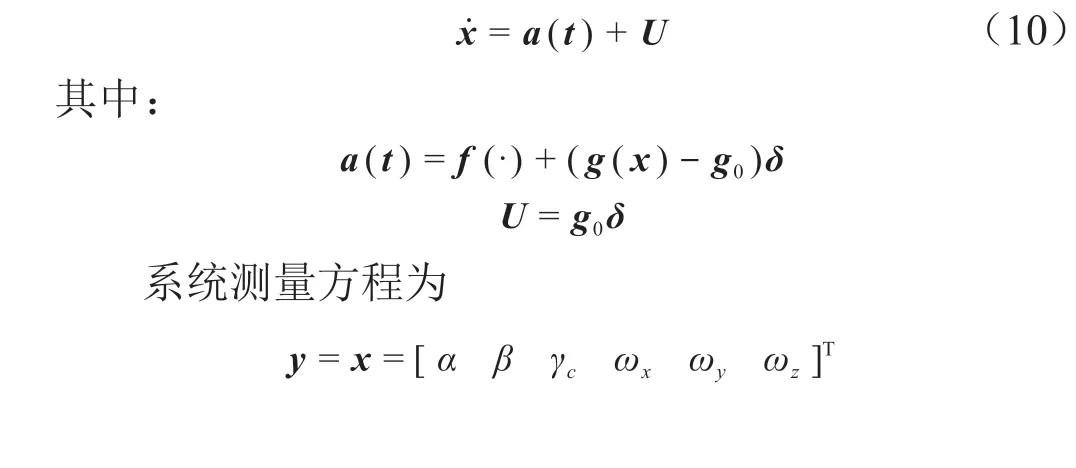
對式(10)的6 個通道均配置相同結構、相同參數的二階ESO。推廣的二階MⅠMO-ESO方程為
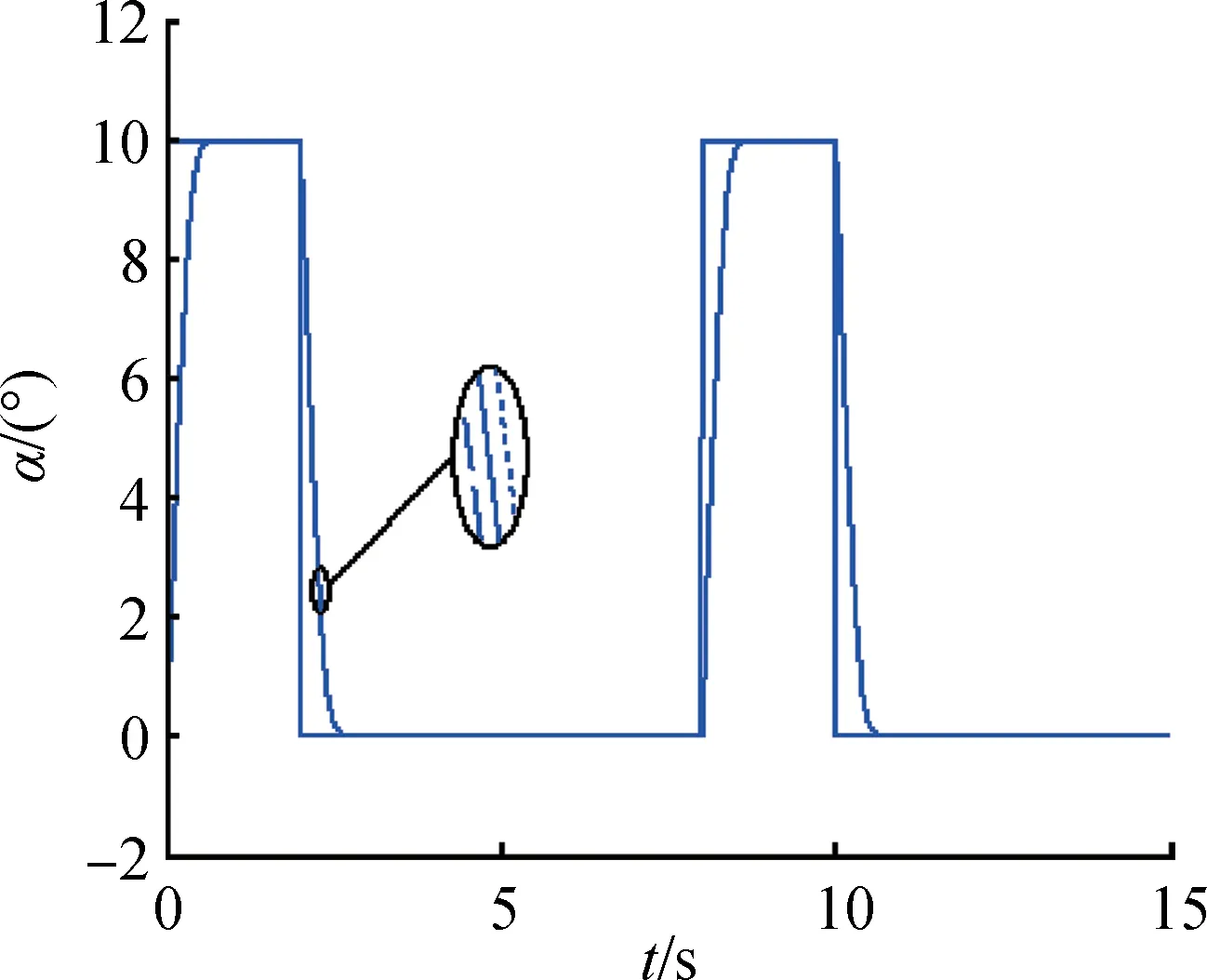
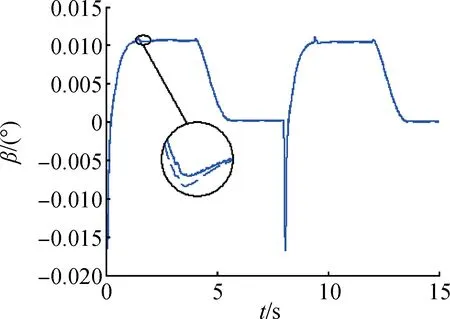
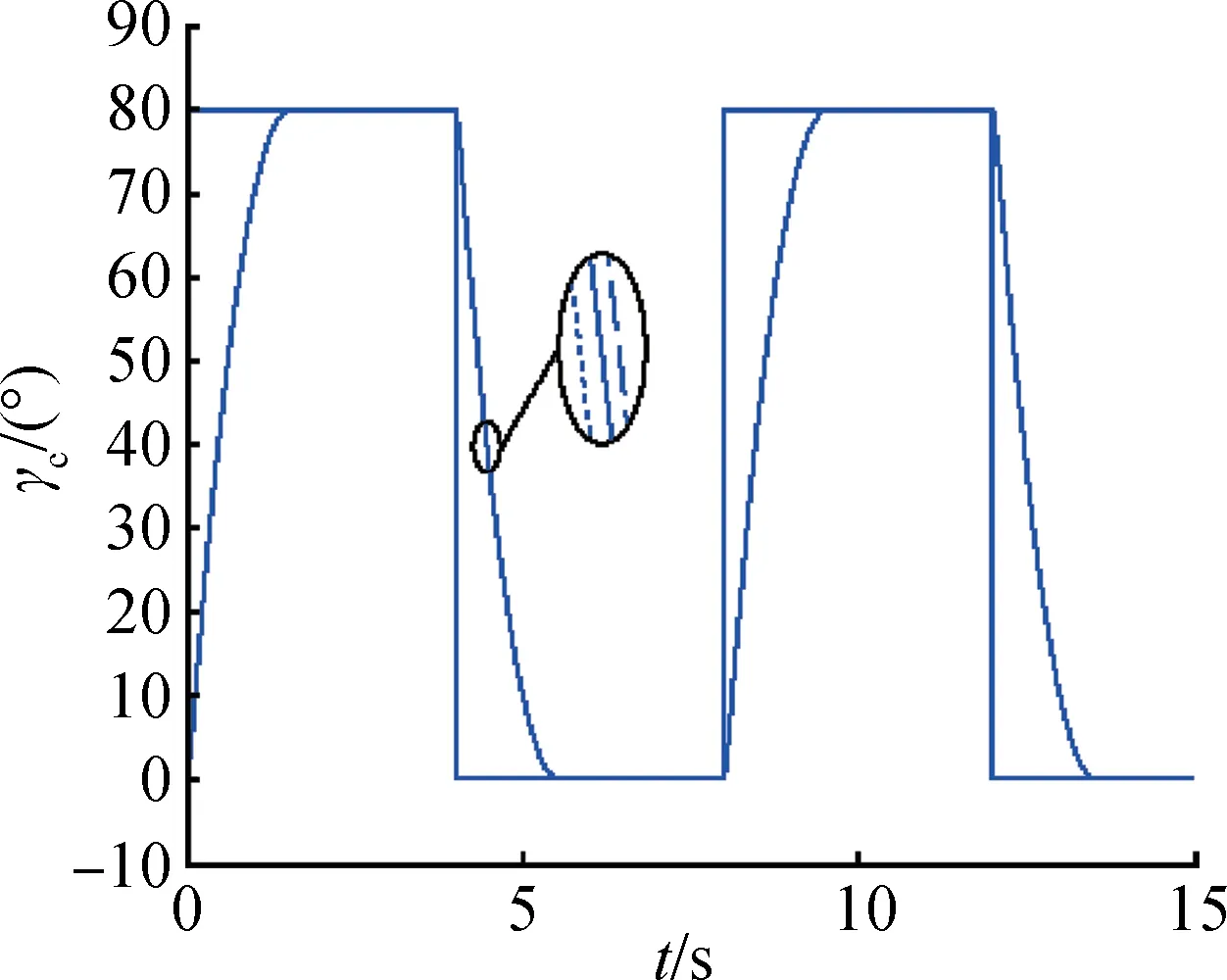
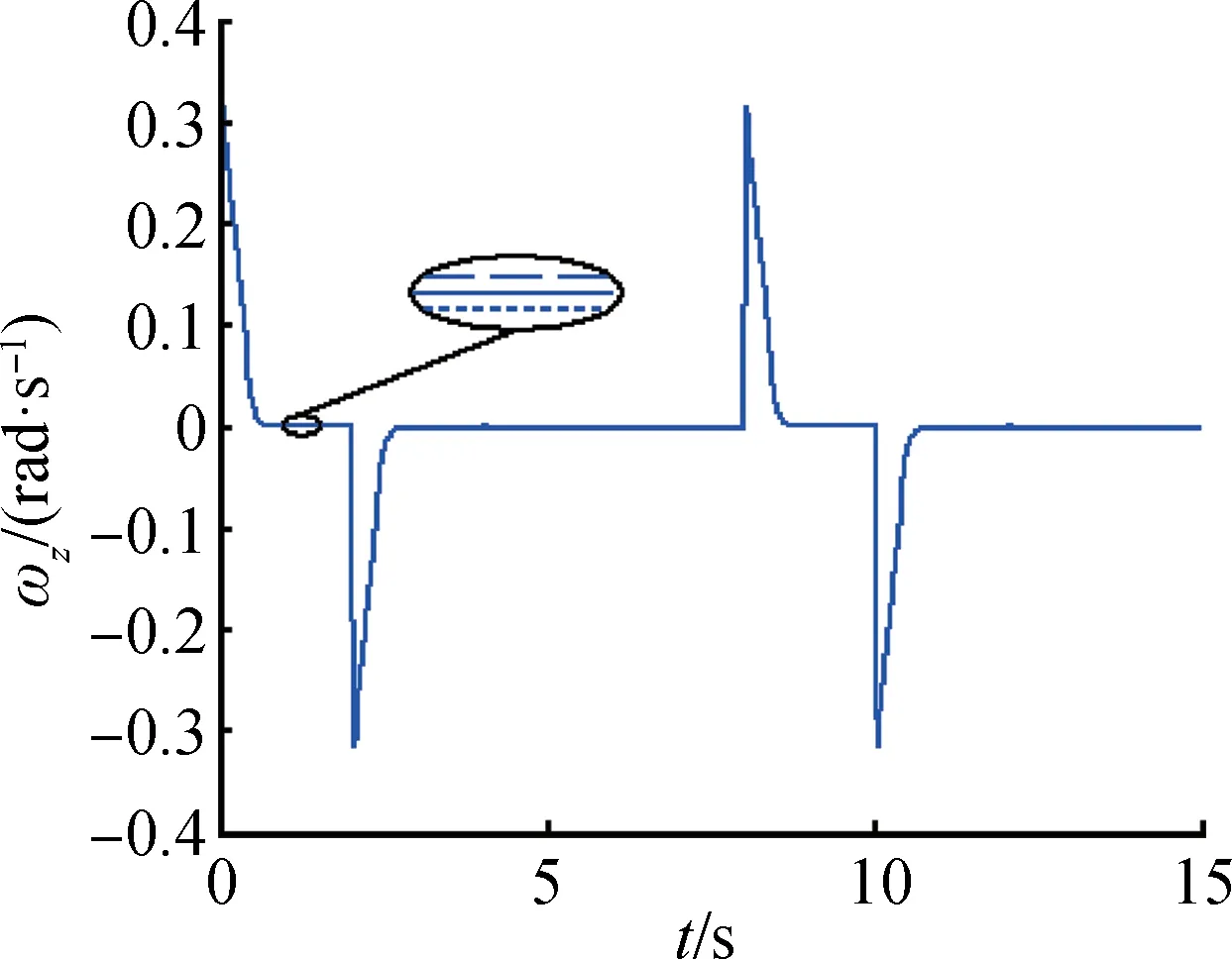
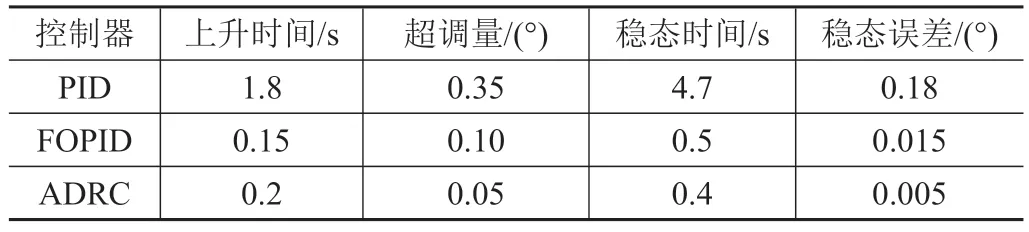
其 中,b11,b12,a1,σ1均為 標量,b11> 0、b12> 0、0 即ESO狀態(tài)將分別實時估計出彈體角速度和模型中總不確定項a(t)。利用估計值z12,對式(8)實施下列動態(tài)反饋補償律: 則式(10)被動態(tài)反饋線性化為單積分系統(tǒng):x?=U0。 可見,動態(tài)補償后,從控制輸入U0至輸出x之間的6個通道成為并行的6個單積分器系統(tǒng),6個通道得到了解耦,并且采用ESO實現這種動態(tài)反饋補償無需已知f(·)和精確的參數值,允許帶有參數攝動、不確定項和干擾影響,因而無需精確的彈體姿態(tài)動力學模型。 盡管ESO對系統(tǒng)總擾動有出色的估計能力,動態(tài)反饋補償后,不可避免地仍存在補償殘差。為了快速抑制補償殘差,控制律采用具有非線性(非光滑)反饋效應的非線性狀態(tài)誤差反饋律,對積分系統(tǒng)進行控制。 非線性狀態(tài)誤差反饋律: 由式(10)可得飛行器操縱舵面的控制指令δ(下式稱為靜態(tài)解耦律): 式(11)~式(15)構成了自抗擾姿態(tài)控制器。 式(9)在MⅠMO-ESO 自抗擾控制器作用下成為如下系統(tǒng): 其中,[A]i表示A的第i個元素。 因此,自抗干擾控制系統(tǒng)的靜態(tài)跟蹤誤差為 定義V=V1+V2,當同時滿足式(22)和式(25)時,V?=V?1+V?2< 0自抗擾控制系統(tǒng)穩(wěn)定。 以某型BTT導彈模型為例進行仿真[15],α?和分別如圖1 和圖3 中實線對應的制導指令信號所示,由BTT導彈的協(xié)調要求直接令β?=0。仿真中角度為弧度單位,輸出轉換為角度單位,氣動參數攝動范圍為±50%,考察控制系統(tǒng)在氣動參數大范圍攝動情況下的性能。 圖1 攻角響應曲線Fig.1 Attack angle 選擇設計參數:b11= 80,b12= 0.001,a1= 0.5,σ1= 0.01;b0= 200,a0= 1,σ0= 0.01。 將上述參數代入式(21),計算可得: 仿真結果如圖1~6 所示,圖1 為攻角響應曲線,圖2 為側滑角響應曲線,圖3 為傾側角響應曲線,圖4~6為角速度響應曲線。其中,實線為標準參數下的跟蹤曲線,虛線為氣動參數攝動50%時的跟蹤曲線,點線為氣動參數攝動-50%時的跟蹤曲線。 圖2 側滑角響應曲線Fig.2 Sideslip angle 圖3 傾側角響應曲線Fig.3 Pitch angle 圖4 軸向角速度曲線Fig.4 Axial angular velocity 圖5 縱向角速度曲線Fig.5 Longitudinal angular velocity 圖6 橫向角速度曲線Fig.6 Lateral angular velocity 仿真結果表明,在標準參數情況下,攻角及傾側角均能快速、無超調地跟蹤制導指令信號,具有良好的動態(tài)品質和較高的跟蹤精度,側滑角滿足|β|≤0.3°的指標,導彈的最大舵偏轉角為10°,最大舵偏轉角速度為40(°)/s。在氣動參數大范圍攝動的情況下,三通道也均能滿足穩(wěn)定性要求,控制系統(tǒng)仍表現出良好的穩(wěn)定性和跟蹤性能,具有很強的魯棒性。 采用相同的被控對象,分別對傳統(tǒng)PⅠD、自抗擾及分數階PⅠD(Fractional Order PⅠD,FOPⅠD)進行仿真對比分析。在期望輸入α=10°的輸入信號中加入噪聲及幅值為10°(第5 s)的脈沖信號,仿真結果如圖7所示。 仿真結果統(tǒng)計見表1。從仿真結果數值可以看出,ADRC 和FOPⅠD 控制器均比傳統(tǒng)PⅠD 控制效果好,上升時間短,響應快。ADRC 相較于FOPⅠD 控制器,上升時間稍大,但超調最小,且具有更高的穩(wěn)定精度。 表1 仿真結果數值Tab.1 Simulation results of value 本文針對高速飛行器再入的姿態(tài)非線性模型,結合自抗擾控制中的擴張狀態(tài)觀測器及非線性狀態(tài)誤差反饋律,設計了具有較強魯棒性的MⅠMO-ESO 自抗擾姿態(tài)控制器,證明自抗擾控制系統(tǒng)穩(wěn)定性的同時,給出了ESO參數選擇和跟蹤誤差計算方法。該方法能夠克服干擾及氣動參數大范圍攝動的影響,在獲取良好的控制性能同時,無需精確的飛行器被控模型,并且對于氣動參數也只需標準值或是估計值,無需知道氣動參數攝動的界限,克服了實際工程中難以建立精確被控模型并獲取參數攝動范圍的困難,具有工程應用價值。

2.2 穩(wěn)定性分析及誤差分析

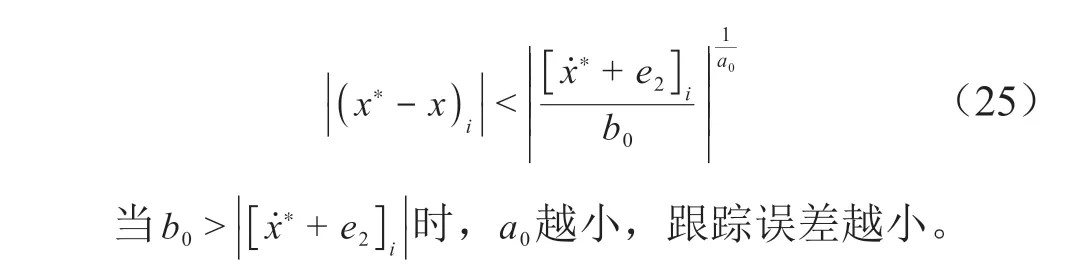
3 仿真分析



4 結束語

