翻轉啟閉機構設計與優化研究

蕭 輝，郭錦炎，李玉龍，王金龍，劉寶龍

（1.北京航天發射技術研究所，北京，100076；2.中國人民解放軍96901部隊，北京，100091）

0 引 言

密閉門是壓力罐的重要組成部分，其啟閉性能的優劣決定了壓力罐的方案可行性及其總體規模。該密閉門要求采用翻轉啟閉方式，開啟前要求翻轉載荷的回轉支點向上運動一個高度以避開壓力罐邊上的控制模塊，然后再進行翻轉；翻轉角度是以往壓力罐翻轉類機構的1.4 倍，驅動載荷是以往壓力罐翻轉類機構最大載荷的4.2 倍，采用以往的翻轉機構根本無法實現。因此提出了多連桿接力、自動開閉鎖技術方案。

綜合考慮上述多個技術難點，在進行該壓力罐密閉門啟閉機構設計時，有必要引入多目標優化方法進行優化設計。多目標優化算法在工程領域的應用較為廣泛［1］，相對于數學規劃法而言，在解決復雜的綜合優化問題中，多目標遺傳算法具有很大的優勢［2］，但對于大型重載啟閉系統，因工程上約束較多，往往難以收斂。基于精英策略非支配排序遺傳算法（Nondominated Sorting Genetic Algorithm ⅠⅠ，NSGA-ⅠⅠ）［3］能夠提高求解效率和求解精度［4-5］。

本文結合壓力罐啟閉機構設計要求，采用機構功能運動化的步序開展了翻轉啟閉機構設計，引入基于精英策略非支配排序遺傳算法，以啟閉角度、啟閉機構體積、最大驅動載荷為優化目標進行了鉸點位置優化，最后結合數值仿真結果驗證了方法的可行性和有效性。

1 機構設計

1.1 原理設計

機構設計的核心內容主要在于機構原理方案設計［6］，典型的四連桿、三連桿機構在各類機械系統中已廣泛使用。實踐證明，這類機構具有很好的可靠性與互換性，這也是各類啟閉系統廣泛采用該類機構的原因。

為實現可靠啟閉，啟閉機構采用單作動缸的驅動模式；為實現大角度安全開啟，采用多連桿串聯續力的方式；為實現開啟和關閉時的自動關閉鎖，第一階段的運動采用四連桿形式，將密閉門前端從鎖座凹槽處滑出，關鎖時運動反之。考慮到啟閉過程的平穩性、機構占空間盡可能小的要求，將作動缸置于密閉門正中間，并采用曲柄將載荷傳至左右兩側的執行機構。

根據上述目的和準則，在組合過程中，為了節約結構空間，可以考慮將不同子機構的部分桿共用，即“一桿兩鉸”［7］、“一桿多用”等方式，得到設計啟閉機構原理方案如圖1、圖2所示。

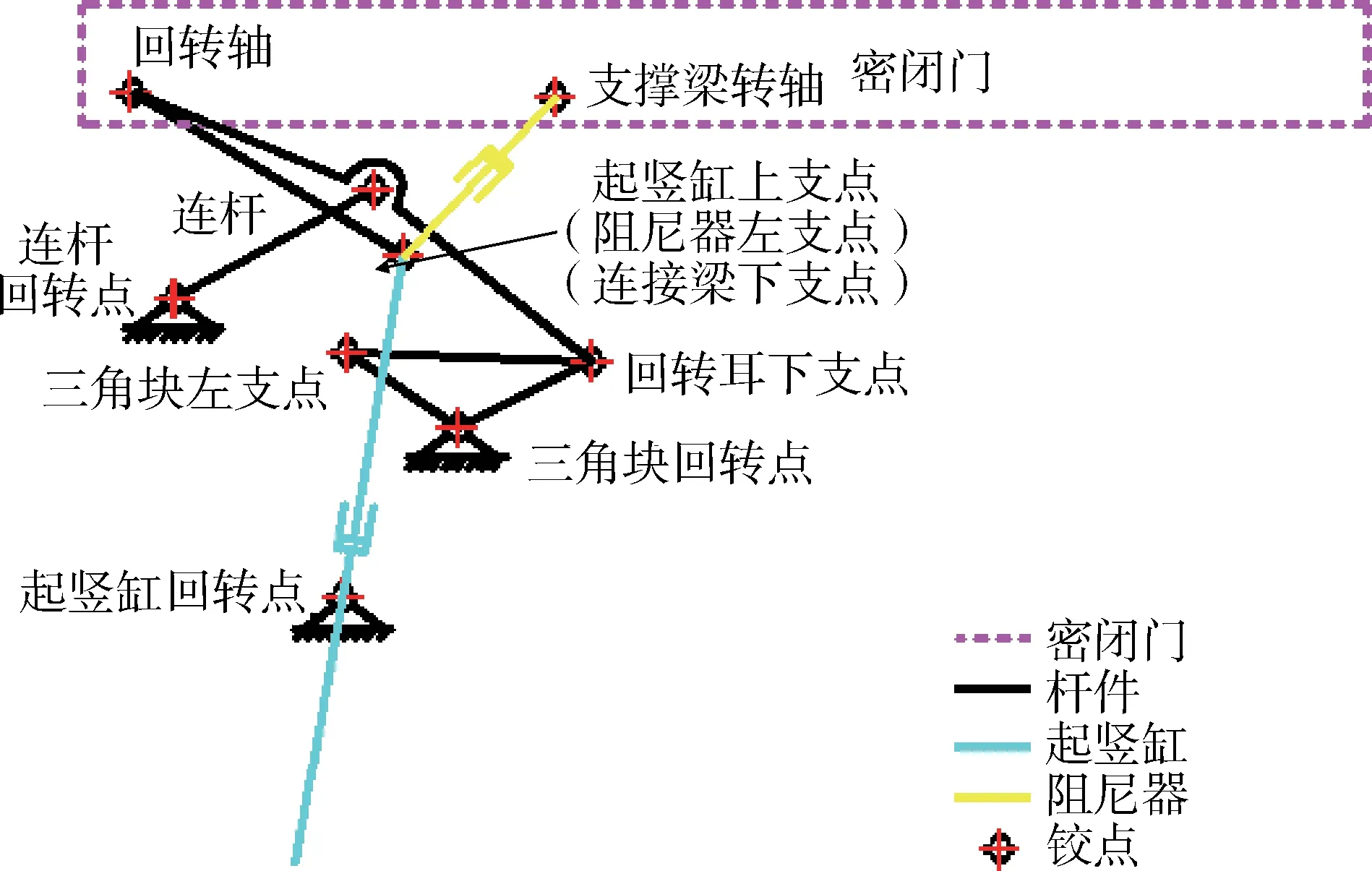
圖1 啟閉機構布置示意Fig.1 Arrangement of the opening mechanism

圖2 啟閉機構動作過程示意Fig.2 The opening process

第二階段動作主要由起豎缸繼續向上伸展實現。此階段四連桿因三角塊左支點已被鎖緊器鎖死，密閉門在起豎缸向上伸展的作用下繞回轉軸轉動，阻尼器在密閉門質心過回轉軸垂面后開始伸展。

第三階段動作主要由阻尼器伸展實現，密閉門在慣性作用下繼續開啟，在達到預定開啟角度前阻尼器減速，直至阻尼器伸展開啟到位。

1.2 計算分析

依據啟閉機構設計原理，建立起動力學理論模型。圖3中示意出三角塊回轉點、回轉耳下支點、回轉耳中支點、連桿回轉點、密閉門回轉軸（回轉耳上支點/轉接梁上支點）。

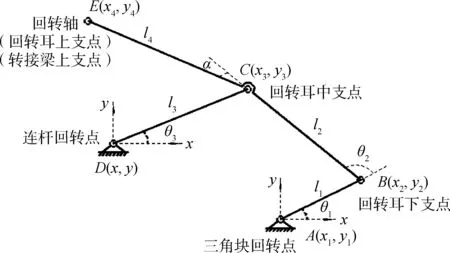
圖3 四連桿舉升機構示意Fig.3 The four-bar linkage

1.2.1 運動學方程

ABCD四連桿舉升機構的運動關系如圖3 所示，可得運動學方程組：

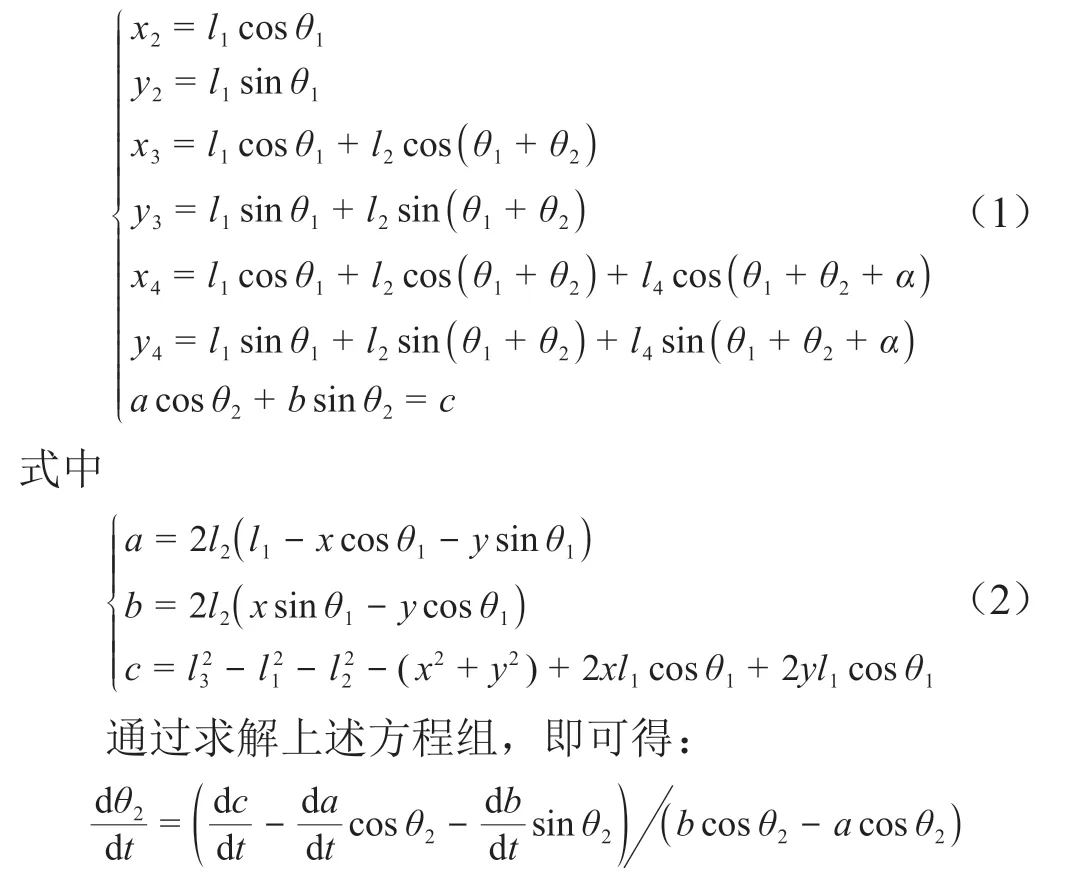
式中

同理可求得四連桿機構其他的運動關系。起豎缸和阻尼器的串聯三鉸點舉升機構的運動學關系較為簡單，在此不再贅述。

1.2.2 動力學方程

密閉門回轉軸力矩平衡示意如圖4所示，因四連桿被鎖死，可認為回轉軸鉸點固支在基座上。

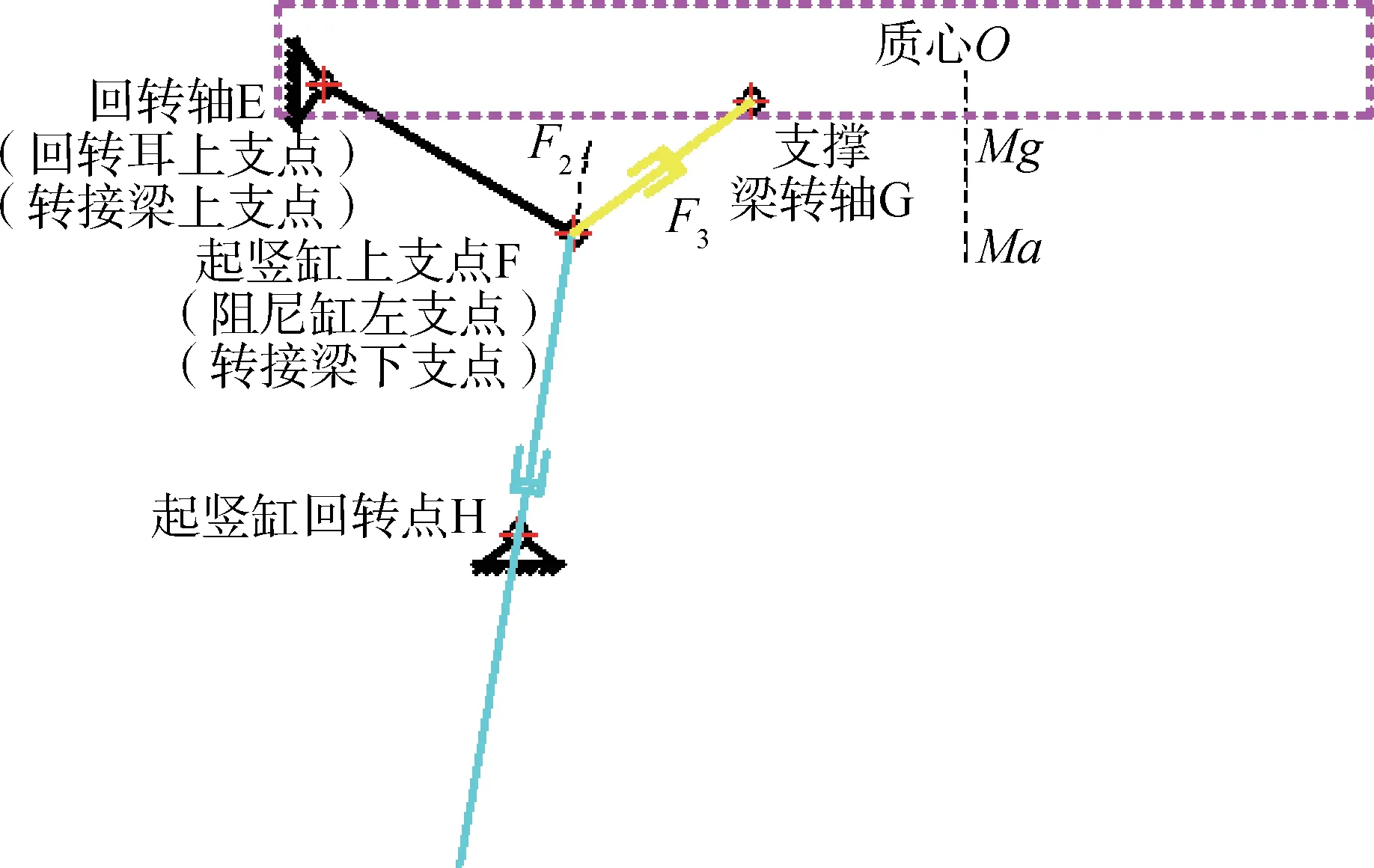
圖4 回轉軸力矩平衡示意Fig.4 Revolution axis moment-equilibrium

在密閉門的舉升和起豎過程中，對密閉門回轉點E取力矩平衡，可得平衡方程：

式中F2為起豎缸提供的驅動載荷；M為密閉門質量；g為重力加速度；a為密閉門在開啟過程中的加速度；Ma為慣性力矩。

在密閉門的翻轉過程中，對密閉門回轉點E取力矩平衡，可得平衡方程：

式中F3為阻尼器給密閉門的作用力。

通過耦合求解壓力罐啟閉機構運動學及動力學方程，即可求得起豎缸和阻尼器的作用力。同樣也可求得其它零部件所受到的作用力。

2 多目標優化

對壓力罐啟閉機構來說，開啟時的載荷環境最為惡劣，故在設計油缸等液壓系統時，主要根據開啟工況載荷分析情況進行設計和選型。同樣，啟閉機構的結構件也是通過提取開啟工作模式下的載荷進行設計。因此本文以開啟工況進行動力學多目標優化研究。

2.1 優化目標

考慮使用安全性和便捷性，開啟角度不宜太小，但太大的開啟角度又對機構和液壓缸的承力提出了更高的要求，因此開啟角度需要綜合多個因素進行匹配和優化。將開啟角度作為優化目標，取開啟角度的小值，但考慮安全性有一個下限要求，即設置開啟角度大于90°作為約束條件，

輕質化、小型化是各類機械結構設計的目標，因此需要減小翻轉啟閉機構所占空間尺寸。考慮到其縱向尺寸（z軸）取決于各桿件寬度和油缸的外徑等參數，優化時暫不做考慮；而垂向（y軸）尺寸涉及到各部件的總體布局問題，僅作約束條件考慮，在進行優化時將整個機構的橫向（x軸）尺寸△x作為優化目標。

起豎缸作為啟閉機構的主要作動缸，其載荷大小直接影響著動力源及液壓系統的選型和布置，故將起豎缸載荷作為優化目標，而其行程僅作為約束條件即可。

綜上，優化目標可表示為min [f1，f2，f3]，其中f1、f2、f3分別為開啟角度、機構橫向尺寸△x和起豎缸載荷。

2.2 設計變量

設計變量主要為各連桿的長度和布置角度，對于參數化的模型來說，主要體現在各鉸點的x軸和y軸的坐標值。

對各鉸點的坐標值優化目標進行靈敏度分析，根據靈敏度分析結果選取鉸點A點、D點、E點、F點、H 點的x軸和y軸坐標（以E 點初始位置為坐標原點，水平向右為x軸正方向，豎直向上為y軸正方向）作為設計變量，用數組X表示。

2.3 約束條件

約束條件主要分為兩部分：

一是來自功能要求相關方面的約束，主要有：

a）翻轉開啟角度不少于90°。

b）機構的垂向總長△y不大于2 m。

c）舉升階段回轉軸的舉升高度為250 mm，此時前端伸出行程不小于85 mm。

d）啟閉機構不能超出安裝空間邊界。

二是主要是來自于諸如結構件和液壓系統設計和布置等工程實現方面的約束，主要有：

a）D點需要位于E點的右側，即xD>xE；

b）開啟時起豎缸載荷不超過185 t；

c）起豎缸第二階段到位后密閉門質心須過密閉門回轉軸的垂面；

d）關閉時在密閉門質心通過回轉軸的垂面前，起豎缸載荷不超過165 t；

e） 起豎缸行程不大于800 mm。

綜上，該翻轉啟閉機構的鉸點優化問題可表示為

式中X為各鉸點坐標參數變量；a和b分別為其對應取值邊界數組值；f1、f2、f3為優化目標；P為等式約束；Q為不等式約束。

2.4 優化流程

程序設計流程如圖5所示。

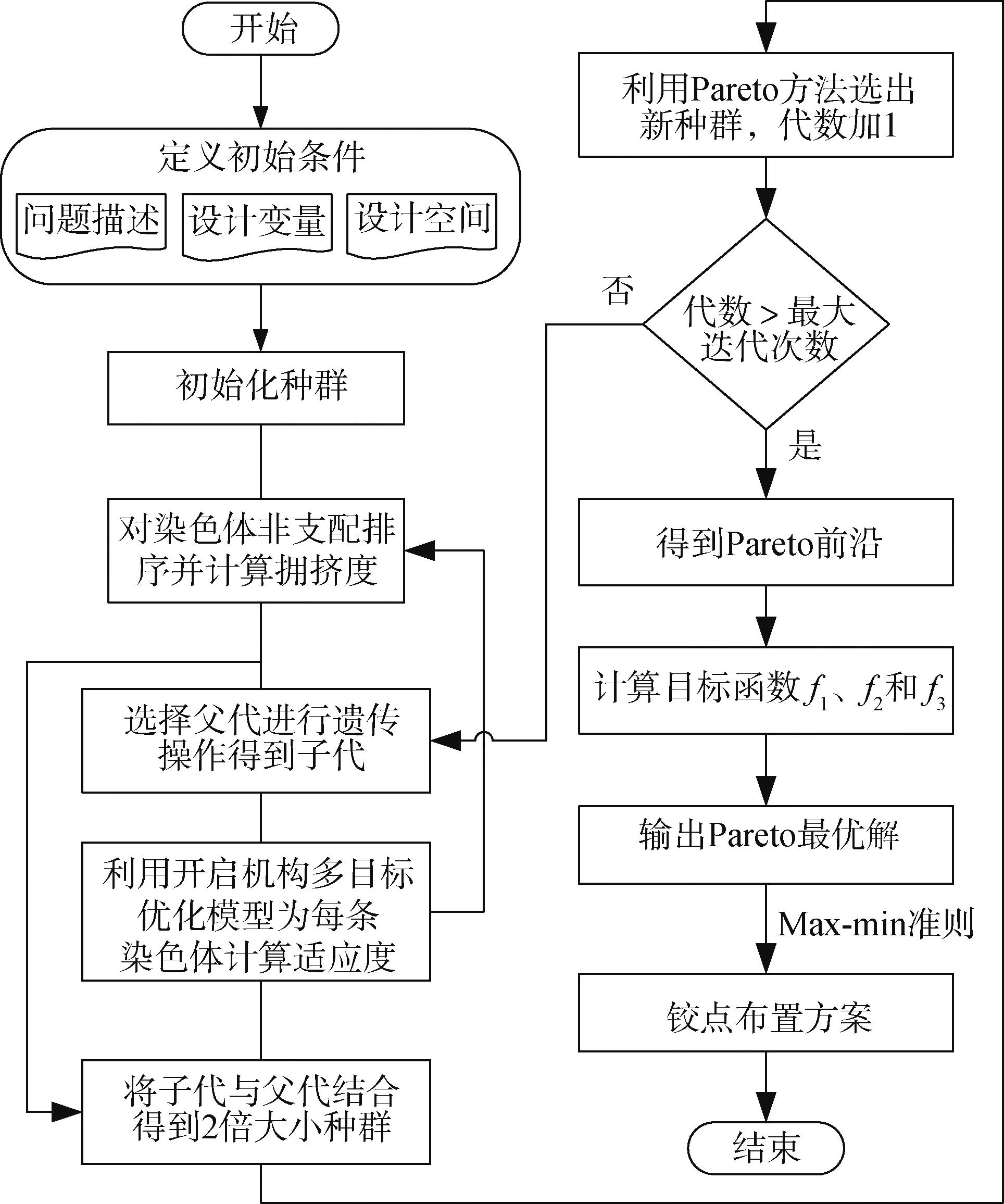
圖5 鉸點優化流程Fig.5 Flow chart of hinge point optimization

如圖5所示，針對上述優化問題，在理論模型的基礎上，引入改進的非支配排序遺傳算法（NSGA-ⅠⅠ），編制多目標優化程序，即可求得該優化問題的Pareto解，再根據Max-min擇優準則［8］即可選得較好的機構鉸點布置方案，見式（7）。

2.5 優化結果

根據上述優化流程，優化后啟閉機構鉸點布局整體方案如圖6所示，優化前后鉸點位置如表1所示。

表1 優化前后鉸點位置變化情況Tab.1 Position comparsion of before-and-after optimization

同時可以得到，優化前后各優化目標值對比如表2 所示。可以看出，優化后開啟角度、橫向尺寸、起豎缸載荷分別增大39.2%、減小16.7%、減小29.6%，有效提高了機構性能。

3 試驗驗證

3.1 仿真驗證

為了驗證多目標優化方法及優化方案的可行性，根據優化前后鉸點布置情況分別進行ADAMS 建模和數值求解計算。因開啟角度和橫向尺寸與連桿鉸點位置、起豎載荷等關聯較大，且目前從工程實現角度來說，起豎載荷的大小是影響著開啟液壓系統設計的關鍵參數之一，因此以最大起豎載荷為目標進行驗證。計算時，采用WSTⅠFF 積分器，SⅠ2 積分格式，進行動力學求解得到起豎缸載荷對比曲線如圖7所示。

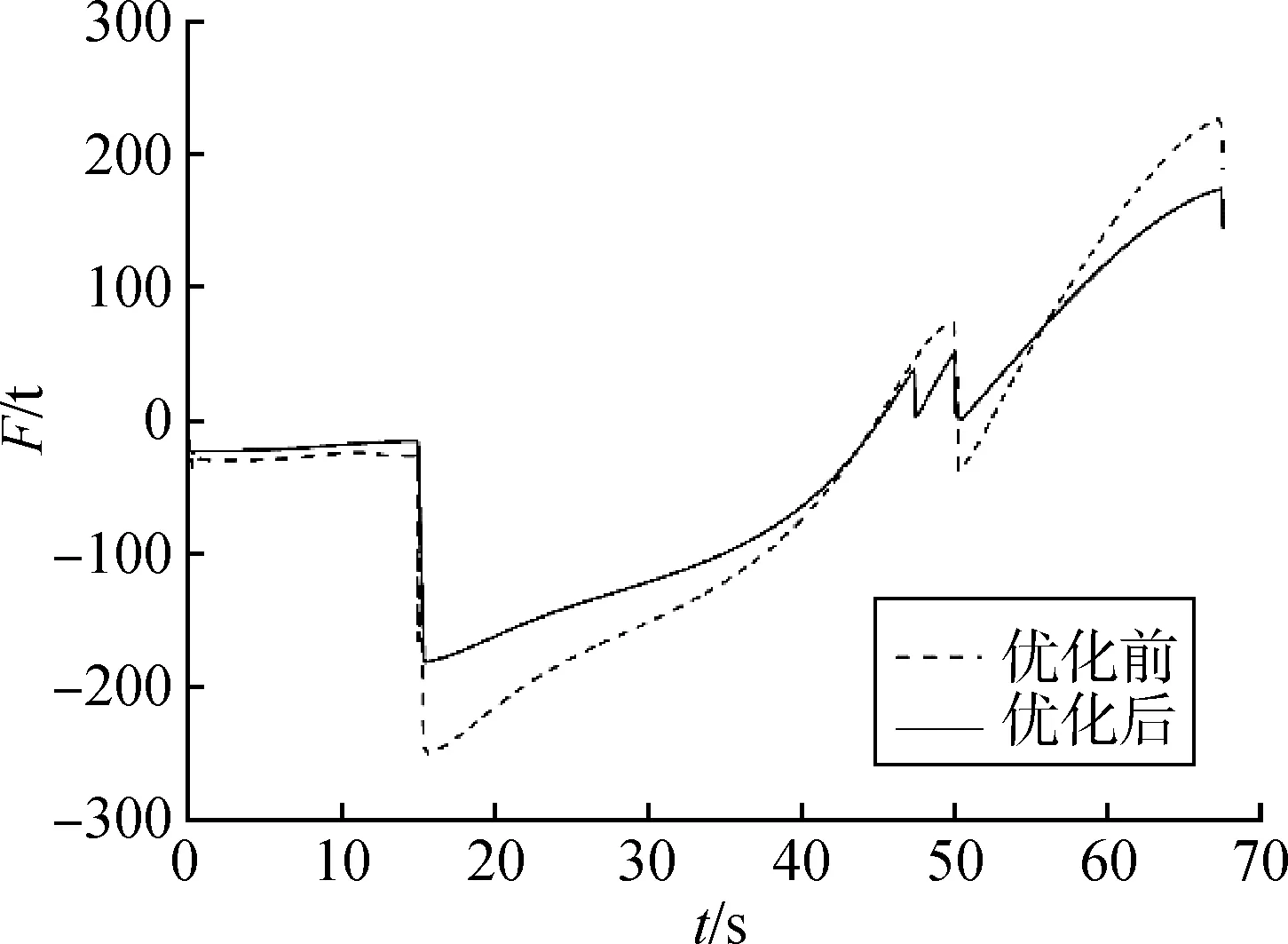
圖7 起豎缸載荷隨時間變化曲線Fig.7 Time history plotcomparsion of erecting cylinderloads

由于起豎缸50 s后就已經達到最大行程，之后的受力均由結構限位來承擔，因此優化時僅考慮前50 s最大載荷。由圖7可知，起豎缸最大載荷由250 t降到175 t，減少了30%，且開啟動作全過程中其載荷值也有不同程度的減少。這個結果與之前多目標優化時的理論計算值（176 t）接近，說明了優化方法的有效性。

3.2 樣機驗證

為了進一步驗證翻轉機構的設計與優化方案的可行性和有效性，研制了對應樣機進行試驗驗證。5 次試驗測試得到折算后的起豎缸平均最大載荷為171 t，這與理論計算值176 t、ADAMS 動力學數值計算值175 t 分別相差2.92%、2.34%，很好地驗證了機構設計與優化的可行性和有效性。

4 結 論

本文應用機構功能運動化的步序設計了可變回轉點開啟結構，構建了參數化機構動力學模型并進行了多目標優化，所得到的優化結果有力地支撐了產品設計。

a）運用多連桿機構時序組合技術，根據機構功能運動化的步序開展了啟閉機構總體方案設計，構建了參數化機構動力學模型；

b）以翻轉開啟角度、機構橫向尺寸、起豎缸最大工作載荷為優化目標進行了機構鉸點位置多目標優化，并運用Max-min 準則從多目標所得Pareto 解集中選出了折中方案，大大提高了翻轉啟閉機構性能；

c）通過動力學數值求解計算及樣機試驗，驗證了該啟閉機構設計與優化方法的可行性和有效性。