精雕細琢 成就高效
—以“二次函數與一元二次方程根的分布”教學設計為例
? 江蘇省海安市立發中學 劉宏俊
眾所周知,高中數學課堂教學“時間緊、任務重”,因此“高效”自然成了課堂教學的最終要求.為了實現這一目標,在日常教學中,教師應該對教學設計精雕細琢,進而形成高效教案,為成就高效課堂保駕護航.筆者以“二次函數與一元二次方程根的分布”為例,呈現高效教案的建構過程,與同行共研.
1 課前自研,設計教案
1.1 研讀教材,確定重難點
學習本課內容前,學生已經學習了零點的概念、零點存在定理,并能夠應用零點存在定理解決一元二次方程根的分布的有關問題.在初中階段,學生已經理解并掌握了應用根的判別式、韋達定理判斷一元二次方程根的情況,同時對二次函數及其圖象也比較熟悉,不過這些知識、經驗在為新知教學提供便利的同時,也可能會形成一定的定勢思維.教學中幫助學生擺脫定勢思維的干擾,學會用圖象法來研究一元二次方程根的分布既是教學難點,也是教學重點.
1.2 預設方案,突破重難點
為了突破重難點,教師需要以學生已有基礎知識為出發點,創設一些目的明確的問題情境,讓學生在問題的引領下突破思維定勢,學會用圖象法解決一元二次方程根的分布問題.預設方案如下:
環節1:回顧舊知,引出主題.
問題1函數的零點概念以及函數存在定理的內容是什么?
問題2一元二次方程ax2+bx+c=0(a≠0)何時有實根?
設計意圖:通過舊知回顧,引導學生將相關知識聯系起來,從而為新知的探究提供依據.
環節2:問題探究,建構知識.
問題1關于x的一元二次方程x2+(m-3)x+m=0有兩個正根,求實數m的取值范圍.
設計意圖:根據預設,大多數學生會應用初中已學的根的判別式或韋達定理來解決問題.利用已有知識和方法解決問題后,教師鼓勵學生嘗試從函數的角度去分析,應用二次函數的圖象來解決問題,并及時引導學生總結歸納不同方法的區別與聯系,促進對知識的理解.
問題2若關于x的一元二次方程x2+(m-3)x+m=0的根滿足以下條件,分別求實數m的取值范圍.
(1)兩個實根均小于1;(2)兩個實根均大于0.5;(3)一個根大于1,一個根小于1;(4)一個根大于0,一個根小于0;(5)兩根均大于0且小于2;(6)兩根中有且只有一個根在區間(0,2)內;(7)一個根在區間(-2,0)內,另一個根在區間(1,3)內.
設計意圖:通過問題的解決,領悟韋達定理的局限性,凸顯函數圖象法的靈活性、廣泛性、方便性,進而領悟研究新方法的必要性.
環節3:應用知識,深化理解.
例1若關于x的方程4x+(m-3)2x+m=0有兩個相異的正根,求實數m的取值范圍.
例2若關于x的不等式x2-4x≥m對于任意的x∈(0,1]恒成立,求實數m的取值范圍.
設計意圖:通過典型例題進一步深化對圖象法的理解,體會函數圖象在解決方程和不等式等問題方面的重要應用,凸顯數學知識間的內在聯系,逐漸完善認知結構.
環節4:課堂小結,升華知識.
在本環節可以預留時間讓學生自主總結,領悟圖象法在解決方程根的分布問題的優越性,歸納應用函數圖象解決問題的一般過程,促進學生已有知識結構的優化,推動學生分析和解決問題能力的提升.
2 合作共研,修訂教案
知識構建是本課教學中的重中之重,基于該環節的問題設計,教師集體研究,提出了如下修改意見.
2.1 情境創設應在知識最近發展區
環節2中,設計問題1的目的是通過舊方法引出新思路.不過在探究問題1的過程中,學生真的能夠想到圖象法嗎?相信大多數學生受慣性思維的影響,很難想到利用函數的圖象來解決問題,這樣也就難以真正起到以舊引新的效果.如果要想達到預設目標,那么只能靠教師講授來實現了,這樣課堂教學又走上了“師講生聽”的老路,學生雖然能理解和掌握新方法,但是卻很難領悟如何想到圖象法.其實,在實際教學中,不必急于強灌,不妨創設認知沖突,讓學生發現已有方法已經難以解決現有問題,然后再引出圖象法.當學生理解了圖象法之后,再回頭分析問題1,進而總結歸納不同方法的區別與聯系,培養學生良好的數學思考習慣,提高學生學習品質.
2.2 問題探索應做到簡潔精練
知識建構階段,教師設計問題2的目的是讓學生學會用圖象法解決問題.在解決問題的過程中,讓學生了解應用圖象法需要從哪幾個角度去分析,知道何時用判別式、何時不用判別式,提高分析和解決問題的能力.問題2中共有7個小題,充斥著題海戰術的味道,這樣會占用較多的獨立思考和自主探究的時間,不利于學生思維能力的發展和自主探究能力的提升.同時,從問題來看,不少題目難度過大,容易造成思維障礙,影響解題信心.另外,問題數量過多,教師沒有充足的時間深入剖析,而為了完成教學任務,不得不繼續“強灌”.基于知識建構階段中存在的不足,教師重新設計環節2中的問題:
問題1關于x的一元二次方程x2+(m-3)x+m=0有兩個正根,求實數m的取值范圍.
問題2關于x的一元二次方程x2+(m-3)x+m=0有兩個實根,其中一個實根大于1,另一個實根小于1,求實數m的取值范圍.
問題3關于x的一元二次方程x2+(m-3)x+m=0有兩個實根,其中一個根在區間(-2,0)內,另一個根在區間(1,3)內,求實數m的范圍.
設計意圖:在解問題1時,學生大多會應用初中所學的韋達定理.在解決問題2時,學生首先想到的也是韋達定理,但是通過分析發現,利用韋達定理難以獲解,此時,教師可以引導學生從函數圖象的角度去分析,通過創設沖突,激發學生探究新方法的迫切感,提高學生參與課堂的積極性.通過問題3進一步呈現圖象法的方便性、靈活性.如此改編,既能讓學生體會圖象法產生的必要性,又能體會圖象法在解題中的廣泛性和方便性.同時,題目“瘦身”后,教師就有充足的時間帶領學生進行深度剖析,開展深度教學.
3 課后反饋,完善教案
3.1 總結提煉,形成體系
環節1中,引導學生回顧一元二次方程的根、函數零點、函數零點存在定理等相關知識,為知識構建作鋪墊.環節2中,通過由淺入深、由易到難、由熟悉到陌生逐層遞進的問題,引導學生自然而然由韋達定理過渡到圖象法,讓學生充分體會二次函數圖象與方程的關系,明確圖象法的實質是零點存在定理的應用.為了幫助學生加深對核心內容的理解,教師可以讓學生以表格的方式進一步總結提煉(如表1).
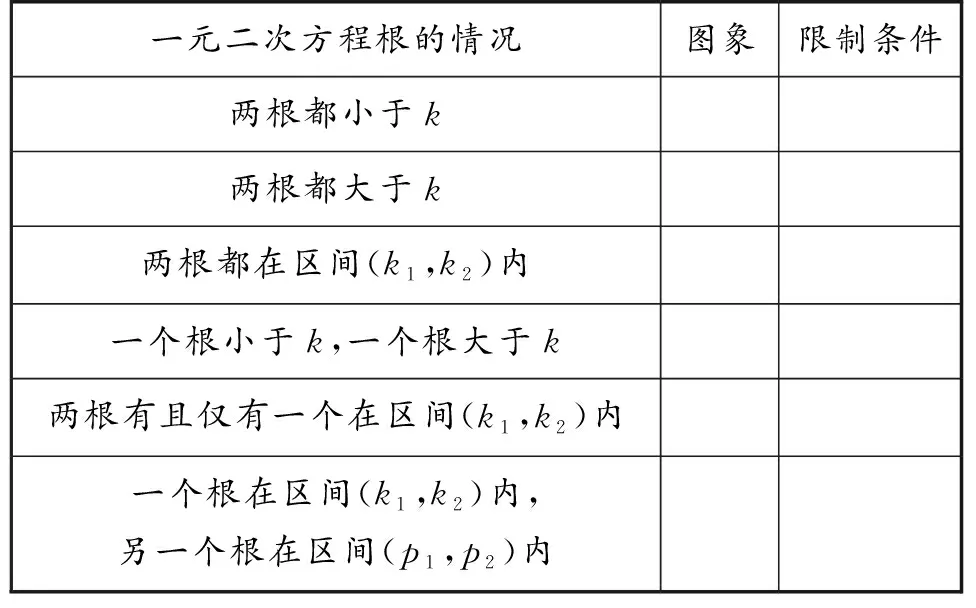
表1
設計意圖:總結提煉是將知識內化為能力的關鍵一步.在學生理解并掌握解決利用圖象法解決一元二次方程根的分布情況后,把問題一般化,讓學生通過自主探究和合作交流進一步明確利用圖象法時從哪幾個角度列出限制條件?何時用判別式?何時用對稱軸?借助有效的總結歸納,使學生的知識結構更加系統化、完整化,實現知識體系的建構.
3.2 層層追問,突破難點
通過集體研究,將問題進一步優化,使得由韋達定理到圖象法的過渡顯得更加自然、順暢.在解決問題的過程中,教師還可以結合課堂生成進行適時追問.例如,在知識建構環節,學生利用韋達定理解決問題后,教師可以追問:“還有其他解法嗎?”又如,學生利用韋達定理求解受阻時,教師可以啟發學生作出二次函數f(x)=x2+(m-3)x+m的圖象,然后根據題意列出相應的關系式.若學生不能完成,可以繼續引導學生思考零點存在定理.這樣層層追問,有利于教學重難點的突破,有利于學生學習能力的提升和數學核心素養的落實.
總之,一堂好課離不開教師的認真打磨、反復錘煉.在高中數學教學中,要充分發揮集體備課的優勢,通過對教學設計的精雕細琢,成就高效課堂.

