三塘湖煤田煤灰熔融性溫度預測模型研究

朱 金 剛

(新疆維吾爾自治區煤炭煤層氣測試研究所，新疆 烏魯木齊 830000)

0 引 言

煤在燃燒和氣化過程中，有時會存在煤灰的結渣問題。煤灰結渣現象與煤灰的熔融特性有很大聯系。因此，煤灰熔融特性是決定鍋爐或氣化爐能否“安、穩、長、滿、優”運行的重要指標之一[1]。煤灰熔融特性通常用煤灰熔融性溫度來表示，即變形溫度(DT)、軟化溫度(ST)、半球溫度(HT)、流動溫度(FT)[2]。由相關研究表明，煤灰熔融特性與煤灰化學成分具有很強的相關性，煤的煤灰化學成分不同，煤灰熔融特性也會出現不同的特點[3-7]。

目前，眾多專家、學者對煤灰熔融特性與煤灰成分之間的關系進行研究，如楊燕梅等[8]通過Factsage軟件研究Si/Al/Na/Ca對準東煤煤灰熔融特性的影響；黃鎮宇等[9]對不同灰成分的低熔點煤灰熔融性調控機理進行研究；劉碩等[10]通過在煤中配入添加劑研究其對煤灰熔融性的影響；張景[11]通過添加助熔劑有效降低煤灰熔融性溫度。研究表明，煤灰成分中的主要物質為SiO2、Al2O3、TiO2、CaO、MgO、SO3、Fe2O3、K2O、Na2O、P2O5等氧化物[12]。SiO2在煤灰成分中的占比相對較高，其質量分數一般為20%～80%，在一定范圍內隨著煤灰成分中SiO2含量的增加，煤灰熔融性特征溫度會出現先降低而后逐步升高的趨勢。Al2O3在煤灰成分中的占比一般為5～50%，隨著Al2O3含量的增加，煤灰熔融性溫度會增加。TiO2在煤灰成分中的含量相對較少，TiO2熔點較高，化學穩定性較好，煤灰成分中TiO2含量越高，煤灰熔融性溫度會升高。CaO在煤灰成分中的占比也相對較高，一定范圍內，隨著煤灰中CaO含量的增加，煤灰熔融性溫度通常會表現出先下降而后上升的趨勢。MgO因與CaO同屬于堿土金屬氧化物，MgO對煤灰熔融性溫度的影響與CaO較為相近，即隨著MgO含量的增加，煤灰熔融性溫度也會表現出先下降而后上升的趨勢。Fe2O3對煤灰熔融性溫度的影響與氣氛有關[13]，在還原性氣氛下，Fe2O3增加會使煤灰熔融性溫度降低。K2O、Na2O在煤灰成分中的含量相對較低，一般情況下，隨著煤灰成分中K2O、Na2O含量的增加，煤灰熔融性溫度會降低。SO3、P2O5含量增加時，通常會導致煤灰熔融性溫度降低。同時，周昊等[14]以煤灰成分為網絡輸入，煤灰軟化溫度為網絡輸出，采用廣義回歸神經網絡對煤灰熔點進行了建模預測。時浩等[15]以煤灰成分及結渣評判指標為自變量，煤灰熔融性溫度為因變量建立了BP神經網絡和最小二乘支持向量機的灰熔點預測模型。結果表明，不同的預測模型及方法會對煤灰熔融性溫度的預測精度產生差異。

然而，由于煤灰熔融是1個復雜的過程，與煤中礦物種類、礦物含量等因素有關，截至目前，還沒有1個高精度模型可以預測所有煤的煤灰成分與煤灰熔融特性之間的關系。因此，研究具體煤田或礦區的預測模型，對實現煤灰熔融性溫度控制和煤炭的清潔高效利用具有重要的意義。

1 試 驗

1.1 試驗原料與測試

系統采集新疆三塘湖煤田70個煤樣。依照國家標準GB/T 1574《煤灰成分分析方法》、GB/T 219《煤灰熔融性的測定方法》的規定進行煤灰成分測試和煤灰熔融性測試。對測試結果進行統計分析，樣品的煤灰成分及煤灰熔融特性溫度的最大值、最小值及平均值見表1。

1.2 預測方法

在實際生產過程中，由于煤灰熔融性溫度相較于煤灰黏溫特性較易獲得，所以通常將煤灰流動性溫度增加50～100 ℃作為氣化排渣的重要參數，并將流動性溫度作為判斷煤種是否可用于氣流床氣化。因煤灰的化學組成較為復雜，不同組分對煤灰熔融特性溫度的影響程度不同，采用多元線性擬合，關聯煤灰成分、硅鋁比、酸堿比與煤灰流動性溫度之間的關系。分別構建3種不同輸入變量模型用于對比，包括4變量輸入參數模型、10變量輸入參數模型和12變量輸入參數模型，其中12變量輸入參數模型是在10變量參數模型基礎上加入了復合參數，即硅鋁比和酸堿比2個參數。同時，為對多元線性擬合方程進行優化，采用逐步回歸分析方法，在眾多的影響因素中篩選出對煤灰熔融性溫度影響較為顯著的因素，將影響不顯著的因素去除，最終建立最優的回歸方程。

2 結果與討論

2.1 煤灰流動性溫度預測模型的建立

根據因變量與自變量之間的關系可以進行線性回歸分析，建立因變量與自變量之間的函數方程，其基本數學模型為：

Y=a1X1+a2X2+a3X3+…aiXi+b

(1)

式(1)中，Y表示因變量，X1、X2、X3、Xi表示自變量，a1、a2、a3、ai表示自變量系數，b表示常數。

因為煤灰流動性溫度與各氧化物之間存在一定的關系，所以，基于多元線性回歸可建立煤灰流動性溫度預測模型，模型建立時選用了三塘湖煤田70個煤樣測試數據中的67組數據。

2.1.1四變量回歸方程

以煤灰成分中質量分數含量相對較高的煤灰成分為自變量，即以SiO2、Al2O3、CaO、Fe2O3為自變量，煤灰流動性溫度為因變量進行線性回歸分析，其回歸方程下：

FT=3.014SiO2+0.798Al2O3+0.196CaO+6.388Fe2O3+1 066

(2)

式中，FT為煤灰流動性溫度，℃；SiO2、Al2O3、CaO、Fe2O3表示相應煤灰成分的質量分數，%。

通過計算知式(2)的相關系數R=0.425，可得出煤灰流動性溫度與煤灰成分中SiO2、Al2O3、CaO、Fe2O3該4種氧化物的一次線性關系并不是太明顯。

2.1.2十變量回歸方程

考慮煤灰成分中其他含量相對較少的成分，以10種煤灰成分(SiO2、Al2O3、TiO2、CaO、MgO、SO3、Fe2O3、K2O、Na2O、P2O5)為自變量，煤灰流動性溫度為因變量進行線性回歸分析，其回歸方程如下：

FT=1.436SiO2-0.385Al2O3-18.324TiO2+1.213CaO+8.012MgO-1.727SO3+1.482Fe2O3-4.505K2O-4.550Na2O+1823.560P2O5+1 084

(3)

其中，FT為煤灰流動性溫度，℃；SiO2、Al2O3、TiO2、CaO、MgO、SO3、Fe2O3、K2O、Na2O、P2O5為相應煤灰成分的質量分數，%。

式(3)的相關系數R=0.966，與式(2)相比較，相關性系數提升幅度較大。

2.1.3引入硅鋁比及酸堿比的回歸方程

硅鋁比是煤灰成分中SiO2與Al2O3的物質量的比或質量比。有時通過煤灰成分對不同樣品的煤灰熔融性進行比較，很難僅從SiO2、Al2O3含量解釋其煤灰熔融性溫度的差異。研究發現，硅鋁比與煤灰熔融性具有較好的相關性。隨著硅鋁比的增加，煤灰熔融性溫度也會相應的降低。其原因可能是硅鋁比增加，礦物質有從高熔點的莫來石轉化為低熔點的鈣長石傾向。

根據煤灰中氧化物離子勢的不同，可將煤灰成分分為酸性氧化物和堿性氧化物，酸性氧化物為SiO2、Al2O3、TiO2，堿性氧化物為CaO、MgO、K2O、Na2O、Fe2O3[16]。煤灰成分中的酸性氧化物之和與堿性氧化物之和的比值稱為酸堿比，通常情況下，隨著酸堿比的增加，煤灰熔融性溫度會出現先減小而后上升的趨勢，其可能的原因是增加的酸性氧化物會與CaO、Fe2O3反應生成鐵橄欖石和鈣長石等低熔點礦物，而當酸堿比增加到一定程度后，熔體中的鐵橄欖石等低熔點物質達到飽和，高熔點的SiO2、Al2O3不再參與反應而以高熔點的晶體形式存在。

硅鋁比及酸堿比作為復合參數，其與煤灰熔融特性有較大的相關性，是影響煤灰熔融特性的關鍵因素[17]。因此,為了綜合考慮硅鋁比(Si/Al)及酸堿比(A/B)對煤灰流動性溫度的影響,將硅鋁比及酸堿比引入回歸方程進行分析,其回歸方程如下:

FT=4.281SiO2-1.750Al2O3-111.665TiO2+1.088CaO+8.784MgO-0.763SO3+1.888Fe2O3-20.144K2O-4.988Na2O+1813.949P2O5-22.511Si/Al-14.902A/B+1 082

(4)

式(4)中，FT為煤灰流動性溫度，℃；SiO2、Al2O3、TiO2、CaO、MgO、SO3、Fe2O3、K2O、Na2O、P2O5為相應煤灰成分的質量分數，%；Si/Al、A/B分別為硅鋁比值、酸堿比值。

式(4)的相關系數R=0.971，與式(3)相比較，相關性系數有了一定提高，由于硅鋁比與酸堿比是基于煤灰成分的非獨立變量，所以相關系數提高程度不大。

2.2 煤灰流動性溫度預測模型優化

逐步回歸分析[18]的原理是將對煤灰流動性溫度影響顯著的變量(煤灰成分)逐個引入回歸方程中，同時將影響不顯著的煤灰成分從回歸方程中去除，如此反復，直到不再有煤灰成分能引入和去除為止，從而保證最后的逐步回歸方程是最優的同時變量相對較少。

為了得到更加精準的預測模型，采用逐步回歸的方法對煤灰流動性溫度進行預測。根據逐步回歸計算原理，得到逐步回歸分析方程如下：

FT=9.608MgO+1.201Fe2O3-4.522Na2O+1814.431P2O5+1 128

(5)

式(5)中，FT為煤灰流動性溫度，℃；MgO、Fe2O3、Na2O、P2O5表示相應煤灰成分的質量分數，%。

從逐步回歸方程中可以看出，回歸方程中包含MgO、Fe2O3、Na2O、P2O5共4種煤灰成分，除Fe2O3是主要煤灰成分外，MgO、Na2O、P2O5均是煤灰中的次要成分且含量相對較少，但其中的次要成分MgO、Na2O、P2O5在此對煤灰流動性溫度影響較為顯著，此現象與礦物間的反應及熱轉化特征有關。溫度升高時，MgO易與Al2O3、TiO2等酸性氧化物形成低溫共熔體，從而影響煤灰熔融性溫度。煤灰中Na的存在會破壞高聚物的結構，Na2O含量的提高可促進具有低熔融性溫度的霞石和鈉長石之形成，P2O5則與煤灰中的含鈣和鎂的礦物反應生成硫酸鹽及磷酸鹽，進而減少鈣、鎂氫氧化物及硅酸鹽的形成，以上礦物質的轉變將會對煤灰流動性溫度產生影響。

2.2.1回歸方程可用性檢驗

采用F檢驗法對所得到的逐步回歸分析方程進行檢驗，其方差分析表見表2。

表2 逐步回歸分析方程的方差分析

由表2知F=196.520，給定顯著水平α=0.01，查F分布臨界值表，F0.01(4.62)=3.64，F=196.520>F0.01(4，62)=3.64，因此回歸方程非常顯著，方程具有實際使用價值。

2.2.2數值檢驗

為了對逐步回歸分析方程的可用性進行檢驗，選取三塘湖煤田3個煤灰樣品作為檢驗對象(3個樣品數據非模型構建數據)，其煤灰成分組成見表3。

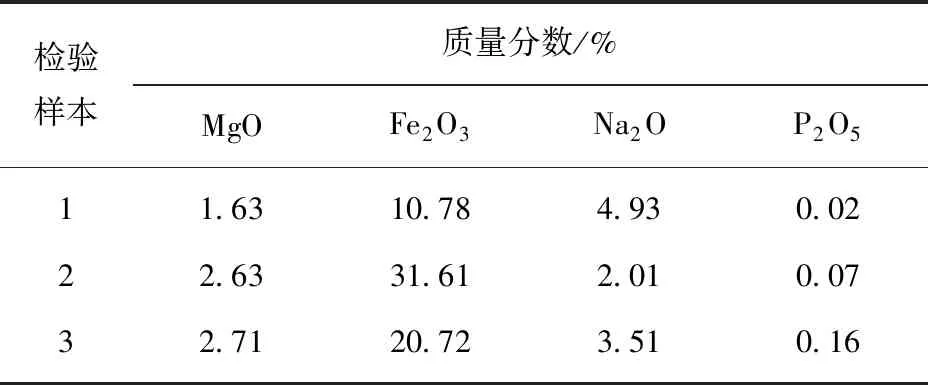
表3 樣品煤灰成分組成

利用式(5)對煤灰流動性溫度進行預測，并將其與實驗室測得的煤灰流動性溫度進行比較，3個樣品的偏差見表4。

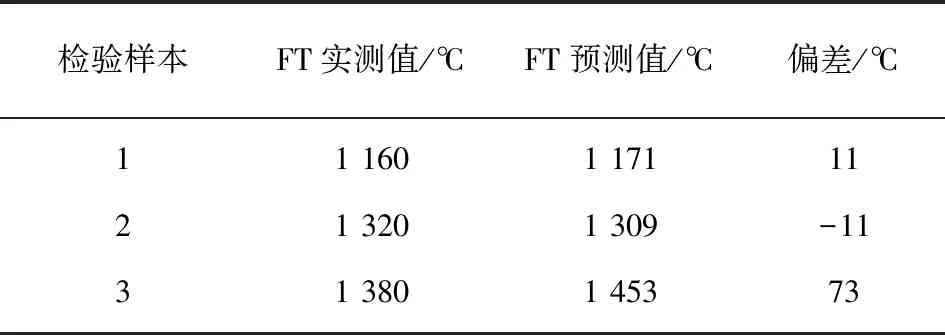
表4 煤灰流動性溫度實測值與預測值偏差

由表4可知，參考GB/T 219中再現性的規定，3個檢驗樣本的預測值與實測值偏差均小于80 ℃，由此推測該逐步回歸分析方程具有較好的預測效果。

3 結 論

(1) 煤灰是各種礦物組成的復雜混合物，煤灰成分常以氧化物的形式表示，不同的氧化物對煤灰熔融性溫度的影響不同，煤灰熔融性溫度受煤灰成分中多種氧化物的影響。

(2) 利用煤灰成分、硅鋁比、酸堿比與煤灰流動性溫度進行不同自變量的線性回歸分析，隨著自變量的增加，方程的相關系數不斷提高。

(3) 利用逐步回歸分析方法對方程進行優化，可得到最優回歸方程。對方程進行F檢驗，顯著性水平為非常顯著，利用該模型對煤灰流動性溫度進行預測并與實測值比較，模型具有較好的適用性，對指導三塘湖煤田煤炭生產實踐具有一定的意義。