幾個三角形不等式的再探究
2024-04-15 06:39:10湖南省長沙市望城區中小學教師發展中心410200劉先明
中學數學研究(江西) 2024年4期
關鍵詞:數學
湖南省長沙市望城區中小學教師發展中心 (410200) 劉先明
設ΔABC的三邊長、三邊對應的高、對應的旁切圓半徑、外接圓半徑、內切圓半徑、半周長分別為a,b,c,ha,hb,hc,ra,rb,rc,R,r,s,用∑、∏表示循環求和、循環求積.文[1] 提供了加拿大數學雜志Crux Mathematicorum 4596題:
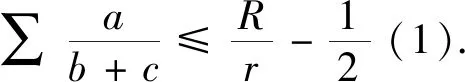
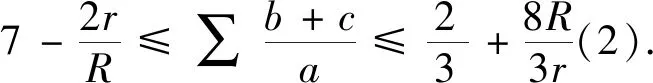
文[2] 提供了加拿大數學雜志Crux Mathematicorum 3450題:
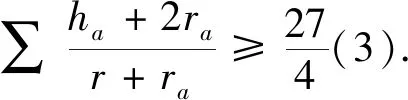
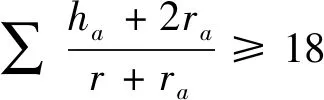
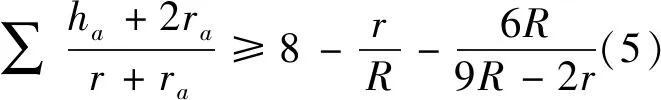

本文獲得(1)、(2)、(5)、(6)式的加強.為證明相應的結論,先給出如下已知的結果.
引理1 (文[4])在ΔABC中,有∑a=2s,∑bc=s2+4Rr+r2,abc=4Rrs,∑a3=2s(s2-6Rr-3r2),∏(b+c)=2s(s2+2Rr+r2).
引理2 (Gerretsen不等式)在ΔABC中,有16Rr-5r2≤s2≤4R2+4Rr+3r2,當且僅當ΔABC為正三角形時取等號.
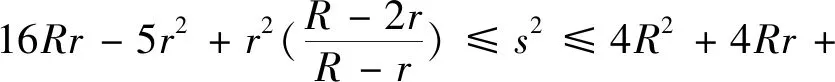
1.(1)式的加強及下確界
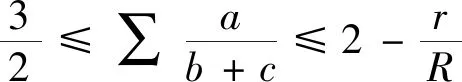
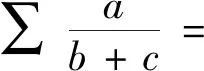
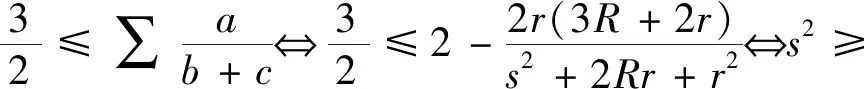
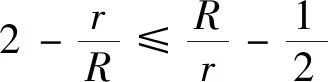
從而結論1是下述Nesbitt不等式的特例.
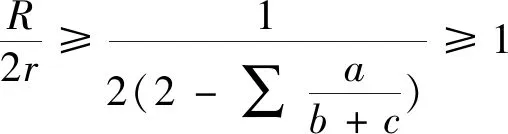
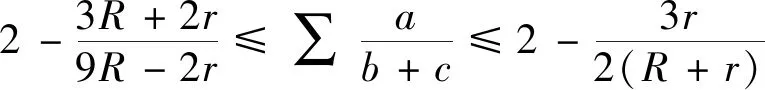
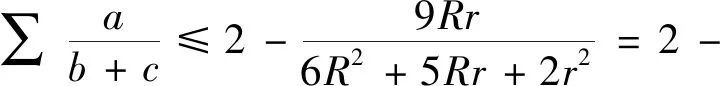
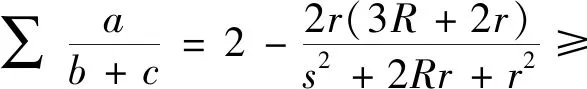
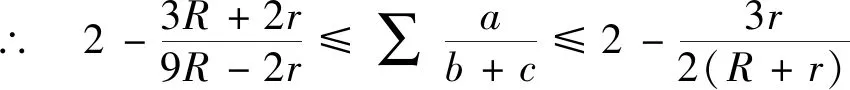
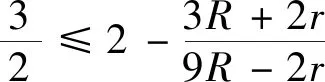
2.(2)式的加強
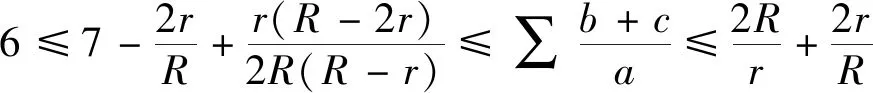
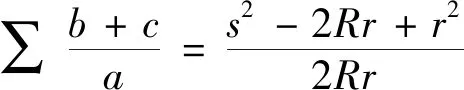
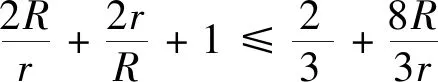
同時,獲得歐拉不等式R≥2r的加強:
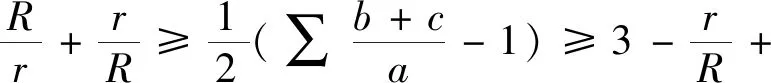
3.(5)式的加強

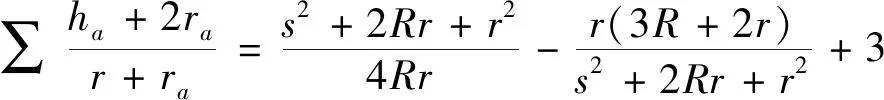
4.(6)式的加強

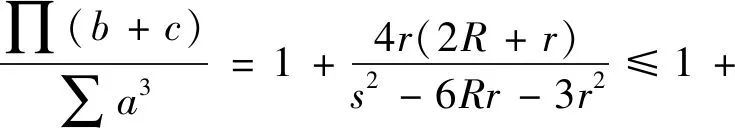
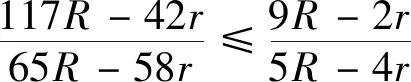
猜你喜歡
中等數學(2021年4期)2021-12-04 13:57:52
中等數學(2021年7期)2021-12-03 04:01:41
中等數學(2021年1期)2021-12-02 03:08:08
中等數學(2021年3期)2021-12-02 00:28:14
中等數學(2020年11期)2020-12-18 01:23:21
學苑創造·A版(2019年5期)2019-06-17 01:14:21
新民周刊(2016年15期)2016-04-19 18:12:04
新民周刊(2016年15期)2016-04-19 15:47:52
傳奇故事(破繭成蝶)(2015年7期)2015-02-28 09:29:27
漫畫月刊·炫版(2014年3期)2014-05-27 04:17:21

