探尋本質 觸類旁通*
——一道解幾中線段比值問題引發的探究

廣東省中山市煙洲中學(中山市周建剛名師工作室) (528401) 周建剛 閆 偉

1 試題呈現

本題為2023年山東省棗莊市3月份高三模擬試題第21題,該題目的命題背景平和,內涵深刻,知識層面主要考查雙曲線的標準方程、幾何性質、直線與雙曲線的位置關系、線段比值問題,是解析幾何專題中的常規題目;重點考查學生運用坐標法研究圓錐曲線中的存在性問題,側重考查學生的數學運算、邏輯推理等素養;試題分兩問,第一問結合雙曲線的焦點坐標和漸近線方程求標準方程,屬于基礎題,第二問尋找滿足線段比值相等的點P,屬于圓錐曲線中探索性的問題,思維難度適中,但運算量較大,需要借助角平分線的性質以及根與系數的關系進行變形轉化,對學生的能力要求較高,較好地體現了對直線與圓錐曲線的核心內容和基本思想方法的考查[1].

2 試題推廣

將題目中的右焦點F改為x軸上的任意一點,不包含雙曲線的頂點和原點,其他條件不變,是否還存在點P滿足上述條件?經探究得到:

圖1

對于直線l與雙曲線交于不同支的兩點,該結論同樣成立,此處不再贅述,留給感興趣的讀者自行證明. 上述性質中F點的縱坐標為零時,就是性質2的結果,即它是性質3的特殊情況.

3 類比探究

將上述性質引申到橢圓和雙曲線中,可得到以下性質:

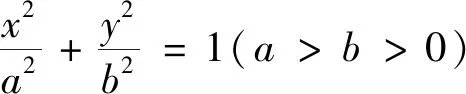
圖2

上述結論中,直線m實際是點F關于圓錐曲線對應的極線,因而P點本質上是過F點與其對應極線垂直的垂線與極線的交點,因此本文中的性質3-5可以進一步統一概括為:

極點與極線是解析幾何中的一條重要性質,它在圓錐曲線問題的探究中具有十分重要的應用,本文對這一線段比值問題的探究很好地佐證了這一點[2]. 近些年很多高考題和模擬試題都以極點、極線相關結論作為命題的落腳點,在復習備考的過程中,引導學生掌握圓錐曲線的極點極線理論不僅能快速高效地解決與之相關的試題,還能有助于學生更深刻、更全面的把握試題的本質[3].