一道2023年模考題的多視角探究
2024-04-15 06:41:36廣東省云浮市黃崗實驗中學527400陳漢邦
中學數學研究(江西) 2024年4期
廣東省云浮市黃崗實驗中學 (527400) 陳漢邦
一、問題呈現與解法探究
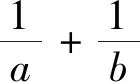
本題是二元約束條件下的二元函數最值問題,試題簡潔、對稱、優美,有一定的難度,本文給出多種視角下的解法.
視角1 拆項+均值不等式
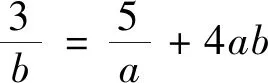
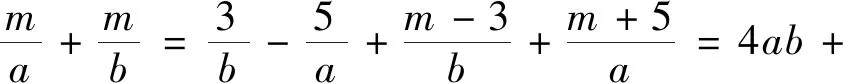
視角2 升冪+比值換元+均值不等式
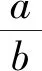
視角3 函數視角
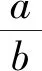
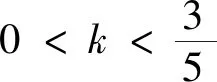
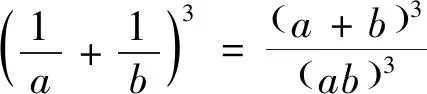
視角4 用求根公式減元
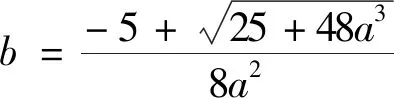
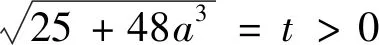
視角5 雙換元+均值不等式

二、變式拓展
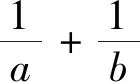

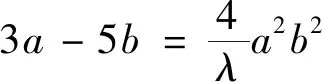
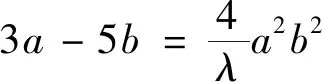
三、試題背景
本題背景是拉格朗日乘數法求極值問題,拉格朗日乘數法時高等數學中求多元函數條件極值的重要方法,方法程序性強,容易掌握,其優點,一是把目標函數和等式約束統一到一個拉格朗日函數中;二是把條件最值問題轉化為無條件最值問題.對文首模考試題,應用拉格朗日乘數法解答如下.
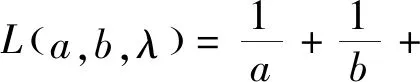
四、追本溯源
本題是一道對思維有較高要求的好題,試題與教材有著緊密的聯系,體現了高考命題源于教材、高于教材的理念.本題來源于人教2019版(數學)選修1第58頁綜合運用第5題:若a>0,b>0,且ab=a+b+3,求ab的取值范圍.這題課本習題就是采用化二元為一元的策略去處理,與本題相通.因此,教師在教學中應重視對課本習題的深度挖掘,挖掘其中蘊含的數學背景、剖析背后的數學本質,感悟試題設計所蘊含的數學思想等.
猜你喜歡
新世紀智能(英語備考)(2021年10期)2022-01-18 05:12:14
新世紀智能(英語備考)(2021年9期)2021-12-06 05:22:38
新世紀智能(英語備考)(2021年11期)2021-03-08 01:10:02
新世紀智能(英語備考)(2020年11期)2021-01-04 00:41:50
新世紀智能(英語備考)(2020年6期)2020-08-14 01:06:24
新世紀智能(英語備考)(2020年12期)2020-04-13 00:50:42
學苑創造·A版(2019年5期)2019-06-17 01:14:21
新民周刊(2016年15期)2016-04-19 18:12:04
新民周刊(2016年15期)2016-04-19 15:47:52
漫畫月刊·炫版(2014年3期)2014-05-27 04:17:21

