基于Shapley 值的作戰體系單元價值評估*

夏庭漢，趙東波，樊 明*，陳清華

（1.北京師范大學系統科學學院，北京 100875；2.解放軍32180 部隊，北京 100076）

0 引言

隨著信息技術的發展，現代戰爭已經轉變為體系與體系的對抗，加快作戰體系能力建設已成為當前軍隊建設的核心任務之一［1］。一般而言，作戰體系是為了追求整體效能而構成的復雜軍事系統，是由多個作戰系統相互協同，按照一定的結構，通過組織、體制、通信及機制連接成一個整體［2］。網絡化是其重要的發展方向，核心特征是不同功能網絡之間的協同作戰，作戰系統內部各功能單元通過信息交互建立起作用關系，組成結構復雜的網絡系統［3］。在作戰體系中，如何快速識別敵方的重要節點進行打擊，或調節信息網絡結構隱藏并保護己方重要節點，是智能化戰爭的熱點問題［4］。

軍事系統中重要節點識別的方法眾多，有基于數學解析、統計數據的評估方法，或者基于作戰環的評估方法，以及基于復雜網絡的評估方法等［5］。其中，基于復雜網絡理論與方法針對作戰體系的關鍵結點、脆弱性等關鍵性問題的研究，或對體系作戰效能進行評估［6］尤為受到關注。張劍鋒等使用復雜網絡方法建立目標價值分析模型，該方法綜合考慮了目標節點以及節點間鏈路的價值，通過網絡生成樹的數目來度量目標的重要性［7］。李茂林等利用度指標、介數指標、緊密度指標和特征向量指標，對作戰網絡中的節點重要性進行評估，并結合最大連通分支、平均路徑長度以及緊密中心性度量作戰網絡在遭受攻擊后的受損程度，提出了在體系對抗中關鍵節點的判定方法［8］。邱原等考慮了網絡中邊的兩個端點對邊本身的重要性影響，有效克服了以邊介數作為重要性指標的片面性［9］。李爾玉等基于作戰節點組合后的整體價值，提出一種基于功能鏈的節點重要性評價方法［10］。張鑫偉等使用熵值法綜合幾類網絡的基本靜態指標進行節點重要性判斷［11］。榮明通過作戰體系彈性仿真實驗建立動態超網模型，提出作戰體系結構彈性指標對作戰體系結構彈性進行分析評估［12］。上述研究從復雜網絡的視角研究體系作戰以及節點重要性等問題，引入了新的研究方向和研究視角，在現代戰爭研究領域發揮著越來越重要的作用。但相當多的研究主要是對于復雜網絡的相關方法技術的使用，并未充分考慮作戰體系的實際特征，對于真實作戰體系的分析有待進一步深入。

本文從作戰體系的整體功能出發，將由指揮、偵察、戰斗、通訊4 種子功能網絡構成的作戰體系抽象為多路復用網絡，在充分考慮網絡整體結構以及軍事目標特性的基礎上，構建了基于Shapley 值的節點價值評估算法，對作戰體系網絡中軍事目標重要性進行評價。該方法也可以結合實際的應用場景進行靈活擴展，具有較好的泛化能力。

1 作戰體系網絡分析及建模

1.1 作戰體系網絡結構

體系作戰是以交戰（物理毀傷與信息對抗）、指控、通信、感知和融合類實體為節點，各實體間的能量、信息和認知交互為邊的復雜戰爭網絡，是具有自組織特征的各類網絡集成的“網絡的網絡”。早期對體系作戰單層同質網絡的建模方法已無法反映信息化條件下體系作戰“多網融合”“跨域交互”的特點［13］。面對新的挑戰，學者們從不同的角度討論了作戰體系的構成，胡曉峰等從物理域、信息域和認知域的角度出發，按照網絡化的組織指揮關系和作戰編成將作戰體系分成3 層的復雜網絡［13-14］。朱濤等將作戰體系分解為基礎信息柵格、戰場感知網格、指揮控制網格和火力打擊網格的4 層立體網格［3］。崔瓊從指揮信息系統的任務、結構和功能角度，構建了基于任務流的指揮信息系統雙層網絡模型［15］。伍文峰針對作戰體系結構動態演化、受人主導和涉及多域交互等特點，建立了體系協同多層時序網絡模型［16］。

結合現代作戰體系廣泛采用的“偵、控、打、保、評”功能域劃分，本文認為作戰體系主要是由相互耦合的四重子網絡組成，整體結構如圖1 所示，分別為通信傳輸網絡、戰場感知網絡、指揮控制網絡和火力打擊網絡［17］。

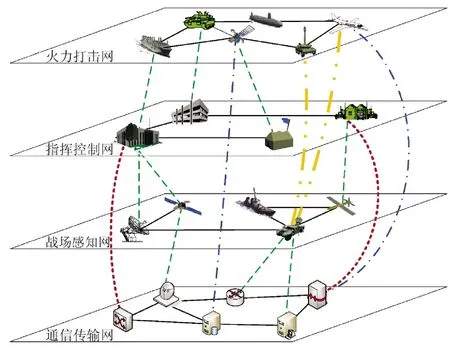
圖1 典型作戰體系網絡結構Fig.1 Network structure of typical combat system

1.2 多路復用網絡模型

多層網絡已成為網絡科學研究的前沿和熱點，它突破了單層網絡中節點和連邊同質性的限制，考慮了多種類型節點及其連邊關系（包括層內連邊和層間連邊）［18］。一個含有M 層的多層網絡可以用超鄰接矩陣G=（A，O）來表示，其中，表示多層網絡中各層的鄰接矩陣集合，表示α 層的鄰接矩陣，表示α層的節點集合，表示層的層內連邊集合，是中的元素：當α 層中節點i 和節點j 有連邊時，，否則。表示層間網絡的鄰接矩陣的集合，元素代表是否存在α 層節點i 到β 層節點j 的連邊，和分別表示α 層和β 層的節點集合，表示α 層和β 層的層間連邊集合。多路復用網絡是一種計算分析更為方便的多層網絡，其所有網絡層由同一組節點構成。該網絡的特點是每一個網絡層表示節點間的某種關系或者相互作用模式，而層間連邊表示同一個節點在不同網絡層的對應關系［19］，如圖2 所示。理論上，可以通過在各層網絡上增添虛擬的節點和邊使得一般的多層網絡都能轉化為多路復用網絡。

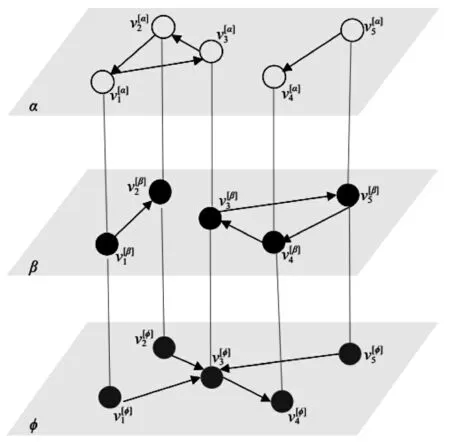
圖2 多路復用網絡示意圖Fig.2 Schematic diagram of multiplex network

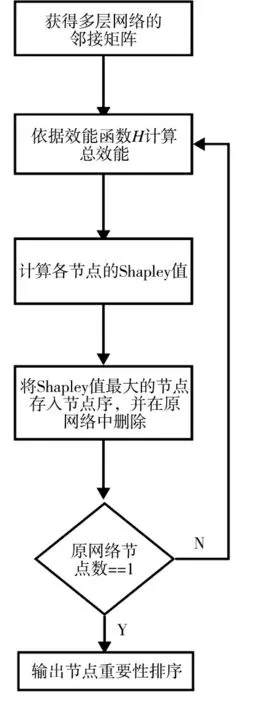
圖3 算法流程圖Fig.3 Algorithm flow chart

作戰體系是一個多維度的系統，具有指揮、通訊、偵察、對抗等一系列的功能，本文假設每個節點都應該具有這4 種功能，只是重要程度不同以及具體表現不同。本文將圖1 中一般性的多層網絡抽象為一個多路復用網絡，其中，跨層的不同節點之間的連接可以將其分解為上層節點在下一層網絡的映射，再由該映射連接至目標節點；從功能的角度來理解，對于每個節點，當其需要進行跨層連接時，它需要先進行功能的切換，實現該節點從一層網絡到另一層網絡的轉化，在新的功能層上進行連接。

2 作戰單元價值評估算法設計

2.1 多層網絡節點重要性評價

復雜網絡研究提出了一系列確定節點重要性的方法，它們分別從網絡的結構、功能等方面來衡量網絡中的重要節點。在軍事網絡研究領域中，常用的有度中心性、介數中心性，PageRank 中心性等指標［8，11］。而在多層網絡中，中心性測度包括節點中心性與層中心性，受到學者的廣泛關注，主要介紹兩種多層網絡節點重要性評價方法。

2.1.1 HD 中心性

文獻［20］中用從多路復用網絡中提取的對單層網絡有效的解來近似多路復用網絡上問題的解，提出了基于多路復用網絡的節點重要性判斷方法HD 和HDA 中心性。HD 中心性利用每層網絡上其節點的度值，對每一層該節點的度值進行乘積，獲得最終對每個的評分。

基于HD 中心性的思路，將前文所提到的單層網絡的中心性指標拓展到多層網絡中去，構建了HB（基于多路復用網絡的介數中心性指標），HC（基于多路復用網絡的集聚系數中心性指標），HE（基于多路復用網絡的特征向量中心性指標）等評價指標。

2.1.2 FMP 中心性

在多層網絡中，PageRank 節點中心性不僅僅取決于指向該節點的數量和質量，還取決于所在層的相對重要性。文獻［21］將其拓展到多路復用網絡，提出了functional multiplex PageRank（FMP）方法量化節點中心性，考慮了節點自身和鄰居的重要性以及所在層的相對重要性。

2.2 目標價值評價指標構建

一個作戰體系的效能是上述多種功能的組合，不同功能的網絡之間相互作用，彼此協作。因此，整體的作戰效能H 可以表示為基于網絡G 的一個函數，也是各個作戰單元的效能Hi的總和：

其中，f 表示各層網絡和各層網絡之間的作用結果，N 為網絡中的節點數。在本文后續的討論中，基于對作戰體系的抽象和簡化，假設集聚系數中心性能夠反映偵察網絡的信息收集聚合能力，介數中心性能夠反映通訊網絡的信息傳播能力，特征向量中心性能夠確定指揮網絡的節點重要性，度中心性能夠反映戰斗網絡的節點重要性。在此基礎上，可以得到一個刻畫網絡整體作戰效能的具體指標：

其中，Ei表示節點的特征向量中心性，Bi表示節點的介數中心性，Ci表示節點的局部集聚系數中心性，Di表示節點的度中心性，α1～α4為權重系數。本文通過設定不同的系數來求解體系不同方面的能力，例如若除α2外其他系數均為0，則聚焦分析整體網絡中的信息傳遞的效能。

節點的重要性是指節點對整個體系作戰效能的貢獻程度，一個節點的重要性不僅在于其直接貢獻，也在于其對其體系中其他部分的支持，二者和越大，那么該節點也就越重要。此外，節點重要性不僅取決于對當前結構的貢獻，還取決于當體系結構發生變化（如其他單元受損）時對體系的貢獻。Shapley 值法通過考慮整個某個節點對于不同組合下的體系整體效能的貢獻，綜合得到每個節點對于體系的真實貢獻。用Shapley 值計算方法如下［22］：

其中，G 為整個網絡，|G|表示其中總共的節點數，H表示該子網絡的效能，S 表示網絡的子網表示S 為網絡G 不包含節點i 的任意子網。S∪{i}表示子網S 加上節點i 后構成的新子網。但上述的Shapley 值的計算方法在節點數量較多的情況下，計算復雜，本文使用文獻［23］中提出的簡化的Shapley值的計算方法以提高計算效率，如下所示：

其中，{vi}∪NG（vi）表示包括節點vi以及它的鄰居的集合，wi，j為節點vi和vj之間的權重，當i=j 時，wi，j=1，Hj是vj的節點效能，Dj是vj的度值。

本文依據該多路復用網絡每一層對應的功能計算其中心性指標，通過式（3）獲得了每個節點的效能。然后對整個網絡進行了一次投影，使其成為一個單層網絡來確定其節點的鄰居，然后計算節點的Shapley 值。

具體的算法流程圖如下所示：

3 節點重要性仿真實驗

3.1 實驗設置

在軍事體系對抗中，不同的角色承擔著不同功能，對應到網絡中即表現為每個節點在不同的網絡中均有著不同的地位。實驗中使用4 層多路復用網絡對作戰體系進行抽象。其中的4 個網絡具有著不同的結構。研究者們經常使用隨機網絡（ER），無標度網絡（BA），小世界網絡（WS）或者規則網絡對作戰體系進行模擬［3，8-9］，本文通過使用ER、BA、WS網絡隨機組合，構建不同的多路復用網絡進行模擬，如表1 所示。其中，每層網絡的節點數都為128 個，平均邊密度為0.1，網絡內連邊數約為820 條。

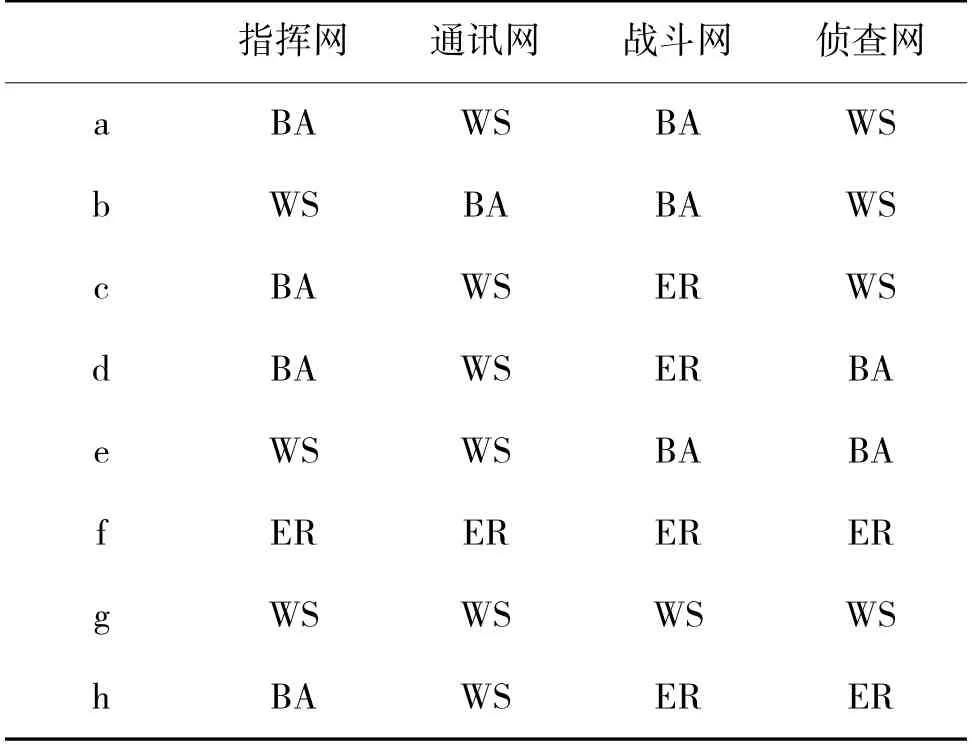
表1 實驗的網絡構成Table 1 Network configuration of the experiment

3.2 實驗結果

基于對網絡的設置，本文對該多層網絡進行節點刪除操作（模擬作戰單元受到攻擊并損壞的情況），使用不同的方法判斷網絡的重要節點并對其進行刪除，比較網絡的整體效能的變化。

從圖4 中可以看到，針對不同的網絡構成形式，基于傳統的節點重要性指標，如介數中心性，集聚系數中心性等并不能穩定且有效對一個多層網絡產生有效的破壞，按FMP 法計算節點重要性的方法與使用Shapley 值判斷出的節點重要性對網絡的殺傷能力相近。

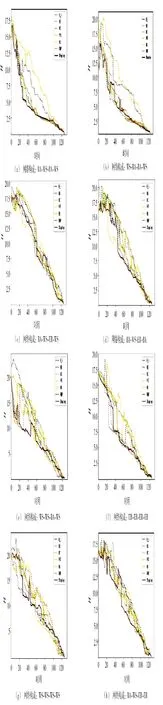
圖4 不同攻擊情況下的網絡效能Fig.4 Network efficiency under different attack conditions

3.3 算法魯棒性檢驗

為檢驗算法的穩定性，以及其對網絡結構的泛化能力，基于同樣類型的基礎網絡類型的設置，本文重復100 次實驗。結果如圖5 所示，箱線圖中統計了依據不同方法判斷的節點重要性順序刪除節點后，網絡整體組織效能曲線所圍成的面積大小，面積越小，代表按照該節點重要性順序刪除節點對網絡的殺傷能力越強。

圖5 不同網絡構成下算法魯棒性檢驗Fig.5 Robustness test of algorithm under different network configurations

比較發現，Shapley 值的方法具有較高的魯棒性，在不同網絡構成下都有較好表現。

基于上述實驗，使用Shapley 值算法對多層網絡進行節點重要性的評估，其效果與FMP 算法相近，優于其他從單一中心性指標考慮的方法。從算法的復雜度而言，FMP 算法有著o（n2）的復雜度，而本文提出的基于Shapley 值的作戰體系節點價值評估方法，復雜度為o（n），要比前者更有效率。

4 結論

本文在充分考慮網絡結構以及軍事特性的基礎上，構建了重要節點發現的Shapley 值算法，對作戰體系中軍事目標進行重要性評價，并結合具體算例進行目標價值評估計算驗證，顯示出較好的性能。利用該算法，可以快速得到作戰目標體系中價值較高的關鍵目標節點，從而支撐決策者進行作戰籌劃。

本文所提出的基于Shapley 值的方法具有較好的可擴展性，可以根據實際運用場景的需求，對網絡結構以及效能函數進行調整并應用于更加復雜的軍事系統中；同時，該方法對網絡結構的依賴性不強，具有很好的泛化能力，可以應用于其他不同結構的社會復雜系統的評價研究中。該方法的不足是需要對網絡結構以及評價指標進行預先的判斷與設置，需要的信息量較大，在實際過程中這一條件很難得到滿足。后續的工作開展中可結合網絡補全等前沿的網絡科學方法，基于部分信息對網絡結構進行推斷，使其具有更加廣泛的應用場景。