基于合情推理能力發展的問題串設計研究

劉園園

［摘? 要］ 邏輯推理素養是數學核心素養的六大素養之一，合情推理作為邏輯推理的一個分支，在數學教學中占有重要地位. 文章從兩個實際案例出發，具體談談合情推理背景下問題串的優勢與設計措施，并從“問題需圍繞合情推理內容而展開”“問題串應立足于學生認知的起點”“應處理好預設與生成之間的關系”三方面談一些思考.

［關鍵詞］ 類比推理；歸納推理；問題串

隨著新課改的推進，教育工作者越來越關注學生的全面發展，“立德樹人”已然成為當下最熱門的話題. 然而，當前仍有部分教師的教育教學理念沒有跟上時代發展的步伐，尤其是課堂中呈現出來的問題串質量不高，無法達到發展學生合情推理能力的目的. 為此，筆者特別針對基于合情推理能力發展的問題串設計進行了大量的研究.

問題串在課堂教學中的優勢

1. 循序漸進，層次分明

以發展合情推理為目標所設計的問題串具有從簡單到復雜、由淺入深的規律. 一個個問題串猶如層層階梯，讓學生能夠在低起點、小步子、多臺階中進行分析與思考，形成自己獨特的見解與猜想，并以推理、總結、驗證等方式總結經驗［1］. 層次分明的問題串能夠夯實學生的知識基礎，讓學生明晰知識的發展過程.

2. 活躍氛圍，引發思考

問題串的介入常能成功地激活課堂氣氛，調動學生的學習興趣，驅動學生產生探索行為. 實踐證明，學生的探索欲往往由好奇心所決定. 章建躍認為，問題具有激發學生去思考、實踐、觀察與學習的作用. 以合情推理發展為目的的問題串，能從較大程度上激發學生的好奇心，提高學生的課堂參與度，引發思考.

3. 環環相扣，建構聯系

問題串與單個問題有著質的區別，單個問題一般以解決一個問題為主，而問題串則由多個環環相扣的問題組成，每個問題之間存在著一定的聯系，學生通過對問題串的思考，可對知識間的聯系產生明確的認識，為建構完整的知識結構奠定基礎. 在問題串的引領下，課堂具有一定的節奏感，每個問題的提出都具有一定的基礎性，同時問題間的關聯性可完善學生的知識體系.

發展合情推理能力的問題串

設計

合情推理是指從事實出發，根據學生自身的認知經驗與直覺推斷出結論的過程. 類比推理與歸納推理屬于合情推理的兩種類型，兩者都是通過觀察、類比、歸納、聯想、猜想等方法驅動學生的探索欲，讓學生從問題串中提升思維能力［2］.

1. 發展類比推理能力的問題串設計

類比推理是指對兩個或兩個以上對象的對比，分析它們之間具備怎樣的異同點，并根據事物的部分屬性推導出其他屬性的過程. 美國著名的數學家波利亞認為，提出新的問題、獲得新的發現都源自類比. 教師在教學中，應從多渠道引發學生的類比，讓學生在問題串的啟發下進行推理分析，以促進數學思維的發展.

案例1? “分式”的教學

分式是初中階段教學重點之一，學生在初始接觸時，常常存在思維障礙. 為了有效發展學生的數學思維，讓學生掌握分式的本質，筆者設計了如下問題串以促進學生類比推理能力的發展.

設計意圖？搖 這三個由淺入深的問題串，意在引導學生通過類比思想的應用，自主獲得分式的概念，讓學生的思維自然而然地從分數過渡到分式，同時對整式到分式的變化過程有一個明確的認識. 此過程不僅滲透了代數思想，還借助問題引發了學生的深度思考，讓學生通過類比思想的應用，自主發現并建構分式的概念，從一定程度上發展了學生的創新意識.

問題4？搖 回顧學習分數時我們研究了哪些內容？（學分數時，研究了分數的概念、性質、運算與應用等）

問題5？搖 與分數類比，你覺得分式應該怎樣學？需要學習哪些內容？

設計意圖？搖 這兩個問題旨在引導學生通過與分數學習過程的類比，自主發現分式知識的學習思路與研究方法，鼓勵學生通過套路，自主發現、建構新知，這是提高學生自主學習能力的關鍵.

問題6？搖 已知一艘輪船位于靜水中的最大航速為20 km/h，該船以最大航速順流行駛100 km所耗費的時間和以最大航速逆流行駛60 km所耗費的時間一樣，求水流速度是多少.

和分數類比，分式與分數的分母不一樣，分數的分母均為整數，但分式的分母是含有字母的整式，因此可以看出分數是分式的一種特殊情況，分式是分數的一般形式.

問題7？搖 以上分式中的字母是否可以隨意取實數？（想要分式有意義，分母不可為0，因此不可以隨意取數）

設計意圖？搖 從生活情境著手引入分式，讓學生結合情境來觀察分式，通過與分數的類比獲取分式的實際意義. 此情境創設的主要目的在于引發學生自主分析分數和分式具有怎樣的關系，并從“是否有意義”的角度來辨別分式應具備的條件.

隨著師生探索的深入，分式的概念與本質也隨之揭曉. 從這個教學過程來看，問題串的應用成功地激發了學生的類比推理能力，讓學生通過與分數的對比，在獨立思考與合作交流中獲得了分式的概念. 這種學習方式，不僅讓學生獲得了一定的研究套路，還使得學生在合作交流中進一步掌握了知識本質，為建構完整的知識結構奠定了基礎.

2. 發展歸納推理能力的問題串設計

歸納是指數學教學中從特殊到一般的過程，歸納推理則是從特殊到一般的推理. 教師應關注學生的實際認識水平與生活經驗，帶領學生從他們所熟悉的事物著手進行研究、總結、概括，以發現一般性的結論. 基于歸納推理的問題串設計，應遵循由淺入深的過程.

案例2? “多邊形的內角和”的教學

學習多邊形內角和難度并不大，學生只要發現并掌握其中存在的規律即可獲得結論. 但其探索過程卻屬于比較困難的環節，若引導不好，學生則難以打開思維，最終只能對公式進行機械性記憶，到后續應用時則漏洞百出. 想要讓學生從根本上掌握多邊形內角和的規律，就要讓學生通過對特殊情況的探索推導出一般性的規律.

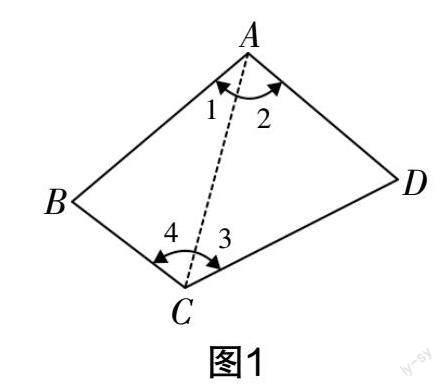
設計意圖？搖 三角形、長方形、正方形、梯形等都是學生所熟悉的圖形，由此作為思維的起點，讓學生思考問題2“是否所有四邊形的內角和均為360°”，這是從特殊到一般的研究過程，學生的思維自然而然地隨之發展，這兩個問題的提出為后續探索多邊形的內角和奠定了基礎.

設計意圖？搖 在問題2的基礎上提出問題3，可成功引發學生的認知沖突，讓學生進入四邊形內角和的探索中去，尤其是方法2的應用，為后續解決多邊形的內角和問題奠定了方法基礎.

方法1中，學生通過量角器的應用，切身體驗了任意四邊形的內角和，這種方法有效提升了學生的動手操作與思考能力. 方法2的應用，有效滲透了化歸思想，成功激發了學生的潛能. 同時，一題多解對發散學生的思維、提煉思想方法以及優化解題技巧具有重要意義.

問題4 ？搖請嘗試應用以上方法分別探索五邊形、六邊形的內角和.

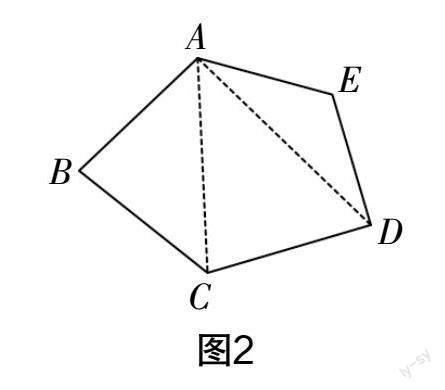
如圖2，從五邊形中的某個頂點出發，分別與其他頂點相連，共有2條對角線，此時原圖形就被分割成3個小三角形，那么五邊形的內角和為3×180°=540°.

如圖3，從六邊形中的某個頂點出發，分別與其他頂點相連，呈現3條對角線，此時原圖形被分割為4個小三角形，由此可以確定六邊形的內角和是4×180°=720°.

設計意圖？搖 循序漸進的問題串讓學生通過對三角形、四邊形、五邊形、六邊形這些特殊圖形的探究，獲得一般性的n邊形內角和的結論：（n－2）·180°. 這種從具體到抽象、從特殊到一般、從簡單到復雜的過程，對發展學生的歸納推理能力具有重要促進作用.

幾點思考

這兩個案例對于培養學生的合情推理能力具有重要意義，不論是類比推理還是歸納推理的發展都離不開問題串的輔助. 如今，問題串在課堂中的應用已經相當普遍，實踐告訴我們，以發展合情推理能力為目的的問題串設計需要注意如下幾點：

1. 問題需圍繞合情推理內容而展開

問題串應用的目的在于引發學生合情推理能力的發展，因此每一個問題的設計都要緊緊圍繞合情推理的內容，將此作為問題的起點與終點. 如案例2中的每一個問題，從表面上看是逐個突破幾邊形內角和，而從本質上來觀察，每個問題都為引發學生發現多邊形內角和規律而準備. 大膽猜想、嚴謹驗證、提煉數學思想方法、歸納公式等都在一個個問題的逐個突破中完成，學生的合情推理能力也在此過程中得以有效發展.

2. 問題串應立足于學生認知的起點

合情推理是有根據的推理過程，絕非毫無根據的胡思亂想. 因此，每一個問題的設計都要有明確的依據，可以學生已有的認知作為問題的起點. 比如案例1中的每一個問題都是在學生原有認知基礎上而設計的，學生的思維隨著問題的深入而發展. 學生從熟悉的分數出發，在問題串的作用下，通過類比推理的方式獲得分式的概念、性質等. 整個過程自然、流暢.

3. 應處理好預設與生成之間的關系

每一節課都是動態發展的，不論多么精心的預設都不能保證課堂能夠根據預設前進. 即使教師根據學生的認知起點來設計問題串，也不能保證每個學生的思維朝一個方向發展［3］. 這就要求教師需擁有隨機應變的能力，根據課堂的實際情況及時調整教學策略.

如案例2中對于四邊形內角和的探索，教師預設了兩種方法，但實際教學中極有可能會出現更多的方法. 此時，教師應啟動應急能力，快速辨別學生所提出的新方法是否適用于多邊形內角和的推導. 若可以，則順應學生的思維，接著往下推導；若不可以，則需做好引導工作，讓學生心悅誠服.

總之，新課標背景下的數學教學以發展學生的數學核心素養為宗旨，以“立德樹人”為核心. 這就要求教師能夠與時俱進地更新教學理念，讓課堂在合情推理中充滿內涵與靈氣. 實踐證明，有問題的課堂是靈動的課堂，有高質量問題的課堂是充滿智慧的課堂，問題串的應用常能讓課堂在“通情達理”中動態生成.

參考文獻：

［1］邵長松. 精心設計數學問題 培養合情推理能力——例談考查合情推理能力的主要方式［J］. 中學數學雜志，2018（04）：20-22.

［2］史寧中. 試論數學推理過程的邏輯性——兼論什么是有邏輯的推理［J］. 數學教育學報，2016，25（04）：1-16，46.

［3］宋運明. 論數學問題提出和數學活動經驗的關系［J］. 數學教育學報，2010，19（06）：34-36，49.