開展合作探究，提升數(shù)學(xué)能力

楊麗瓊

［摘? 要］ 合作能力是學(xué)習(xí)能力之一，在促進(jìn)學(xué)生長期的發(fā)展中具有非常重要的意義. 在數(shù)學(xué)課堂教學(xué)中，要通過創(chuàng)設(shè)合作學(xué)習(xí)的環(huán)境，精選合作學(xué)習(xí)的內(nèi)容，把握合作學(xué)習(xí)的時機(jī)培養(yǎng)學(xué)生的合作意識，以合作探究的開展，提升學(xué)生思考分析、自主學(xué)習(xí)、邏輯推理等數(shù)學(xué)能力. 在合作學(xué)習(xí)中，學(xué)生能夠通過互相協(xié)作，共同完成學(xué)習(xí)任務(wù)實現(xiàn)優(yōu)勢互補(bǔ)，增強(qiáng)學(xué)習(xí)信心，進(jìn)一步激發(fā)學(xué)習(xí)興趣.

［關(guān)鍵詞］ 合作探究；思考分析；數(shù)學(xué)能力

合作能力是能夠與他人圍繞學(xué)習(xí)目標(biāo)，共同分析問題，探尋解題思路的一種能力. 它是學(xué)生成長必備的一種能力，也是取得成功的必備條件. 在初中數(shù)學(xué)教學(xué)中，教師要創(chuàng)設(shè)合作學(xué)習(xí)的條件，引導(dǎo)學(xué)生在合作中學(xué)習(xí)、在合作中成長，通過師生合作、生生合作，提升學(xué)生的合作能力，培養(yǎng)學(xué)生的合作精神. 筆者結(jié)合教學(xué)實踐談一談在課堂教學(xué)中開展合作探究學(xué)習(xí)的一點思考，與各位同行交流探討.

創(chuàng)設(shè)良好的合作學(xué)習(xí)氛圍，強(qiáng)化

合作意識

在日常教學(xué)中，開展合作學(xué)習(xí)的機(jī)會較少，因此教學(xué)中教師要有意識地滲透合作意識，提升學(xué)生的合作能力. 教師要營造平等交流、輕松愉悅的課堂氛圍，為開展合作學(xué)習(xí)創(chuàng)造條件，使學(xué)生在良好的課堂氛圍中不斷強(qiáng)化合作意識.

1. 開展趣味活動，活躍課堂氣氛

初中生活潑好動，對新知充滿好奇心，他們喜愛有趣的活動，因此課堂教學(xué)中要通過有趣味的活動吸引學(xué)生的注意力，使學(xué)生在共同參與的活動中互幫互助、合作交流，共同成長.

案例1? “相似三角形”的教學(xué).

教學(xué)活動：現(xiàn)在我們需要測量學(xué)校操場旗桿的高度，請同學(xué)們分小組設(shè)計測量方案，并選擇一種或幾種測量方案進(jìn)行計算，最后將結(jié)果記錄下來并展示.

設(shè)計意圖? 本例中教師引導(dǎo)學(xué)生以小組合作的方式測量學(xué)校操場旗桿的高度，使學(xué)生在輕松趣味的活動中靈活運用相似三角形的知識進(jìn)行計算，既能激發(fā)學(xué)生的學(xué)習(xí)興趣，又能讓學(xué)生在合作學(xué)習(xí)中深化對知識的理解，激發(fā)其合作意識.

2. 設(shè)計開放性問題，激發(fā)創(chuàng)新意識

開放性問題以豐富的解決思路和多樣化的答案能夠調(diào)動學(xué)生思維的積極性，激發(fā)學(xué)生的創(chuàng)新意識，因此教師可以通過設(shè)計開放性問題，在合作中激發(fā)學(xué)生的思維潛能，提升學(xué)生的思維能力.

案例2? “互逆命題”的教學(xué).

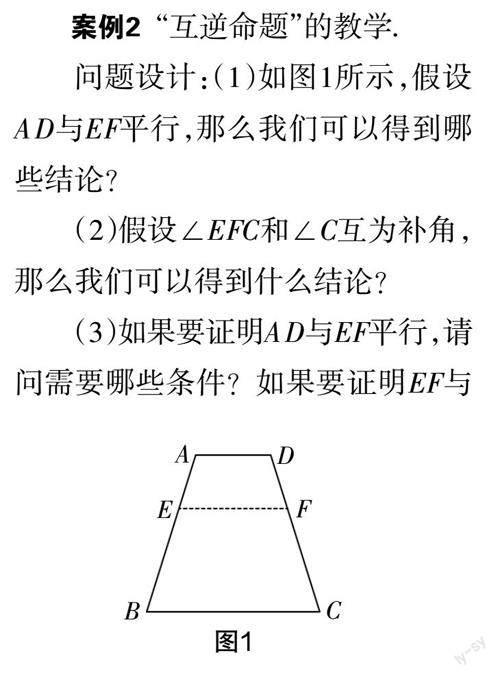
問題設(shè)計：（1）如圖1所示，假設(shè)AD與EF平行，那么我們可以得到哪些結(jié)論？

（2）假設(shè)∠EFC和∠C互為補(bǔ)角，那么我們可以得到什么結(jié)論？

（3）如果要證明AD與EF平行，請問需要哪些條件？如果要證明EF與BC平行，請問需要哪些條件？

（4）回顧你解答前三個問題的過程，請問你運用了哪些數(shù)學(xué)理論？這些數(shù)學(xué)理論間具有什么樣的關(guān)系？

設(shè)計意圖? 本例中的開放性問題有兩種形式，第一種是結(jié)論的開放性，第二種是條件的開放性. 在解決上述幾個問題的過程中，學(xué)生憑借自己一個人的力量很難將問題完全搞清楚. 因此，教師需要引導(dǎo)學(xué)生采用合作學(xué)習(xí)的方式，通過互幫互助，取長補(bǔ)短，從而實現(xiàn)問題的解決，并加強(qiáng)學(xué)生的合作意識，提高學(xué)生的學(xué)習(xí)效率，增強(qiáng)學(xué)生的學(xué)習(xí)信心.

精選合作探究學(xué)習(xí)內(nèi)容，提升

合作學(xué)習(xí)能力

教師要積極發(fā)揮教學(xué)中的主導(dǎo)作用，把握學(xué)生的探究方向，啟發(fā)學(xué)生合作學(xué)習(xí). 在教學(xué)中，教師要精選有探究價值的例題和習(xí)題，引導(dǎo)學(xué)生在合作探究中學(xué)習(xí)，深化合作學(xué)習(xí)的價值，提升課堂教學(xué)效果.

1. 設(shè)計一題多解的訓(xùn)練，培養(yǎng)合作意識

許多例題和習(xí)題都有多種解答思路，一題多解的訓(xùn)練能夠激發(fā)學(xué)生的創(chuàng)新意識，培養(yǎng)學(xué)生思維的靈活性. 同時這類例題和習(xí)題能夠使學(xué)生在相互合作中碰撞出思維的火花，產(chǎn)生更多的靈感，從而生成多種多樣的解答思路，有效提升學(xué)生的合作能力.

案例3? 如圖2所示，已知點A和點B的坐標(biāo)分別為（－1，2），（2，－1），點O為坐標(biāo)原點，求△AOB的面積.

生1：如圖3所示，我覺得可以用矩形覆蓋△AOB，然后減掉多余的部分就能得到△AOB的面積了.

生2：如圖4所示，我采用的是類似的方法，即用直角三角形覆蓋△AOB，然后減掉多余的部分可得△AOB的面積.

生3：如圖5所示，可以先求出直線AB的解析式，再計算出直線AB與y軸的交點C的坐標(biāo)，以及直線AB與x軸的交點D的坐標(biāo)，然后將△AOB分成△AOC和△BOC，或者將△AOB分成△AOD和△BOD，最后所分成的兩個三角形的面積相加就可以得到△AOB的面積了.

設(shè)計意圖? 本例通過一道多解的習(xí)題引發(fā)學(xué)生進(jìn)行討論和探究，鼓勵學(xué)生將自己的解題思路與同學(xué)進(jìn)行分享和交流，在合作中通過優(yōu)勢互補(bǔ)、互相啟發(fā)，生成更多的新智慧. 一題多解考查的是學(xué)生思維的靈活性和多元化，但學(xué)生個體往往很難將所有思路都展現(xiàn)出來，這需要教師引導(dǎo)學(xué)生在合作交流中將思維碰撞出火花，使學(xué)生產(chǎn)生新的靈感，實現(xiàn)新的突破，促進(jìn)學(xué)生共同進(jìn)步，幫助學(xué)生在輕松愉悅的氛圍中獲得知識增長和能力提升.

2. 設(shè)計拓展延伸問題，拓寬學(xué)習(xí)視野

在學(xué)生掌握知識和技能的基礎(chǔ)上設(shè)計拓展延伸問題，可以提高學(xué)生的思維能力. 拓展延伸問題一般具有一定的挑戰(zhàn)性，是激發(fā)學(xué)生探究好奇心的重要載體. 在教學(xué)中，教師需要根據(jù)學(xué)生的認(rèn)知水平設(shè)計適當(dāng)?shù)耐卣寡由靻栴}，可以組織學(xué)生共同探討，從而在合作中保證學(xué)生的探究興趣.

案例4? “反比例函數(shù)”的教學(xué).

（1）請分別求出m，n，k的值；

設(shè)計意圖? 本例是對反比例函數(shù)知識應(yīng)用的拓展，學(xué)生在教師的引導(dǎo)下通過合作探究能夠靈活地解決問題，反比例函數(shù)與不等式相結(jié)合可以拓寬學(xué)生的視野. 面對具有一定挑戰(zhàn)性的拓展延伸問題，學(xué)生在合作中如果能夠明確解決思路，不僅可以提高解決問題的效率，還能夠增強(qiáng)合作學(xué)習(xí)的信心，進(jìn)一步完善知識結(jié)構(gòu).

精準(zhǔn)把握合作學(xué)習(xí)時機(jī)，提高

合作學(xué)習(xí)效率

合作學(xué)習(xí)是提高學(xué)生學(xué)習(xí)效率的一種方式，教師要做好組織和協(xié)調(diào)工作，把握合作學(xué)習(xí)內(nèi)容，抓住合作學(xué)習(xí)時機(jī)，引導(dǎo)學(xué)生采用恰當(dāng)?shù)膶W(xué)習(xí)方法，增強(qiáng)合作學(xué)習(xí)的效果. 另外，對于課后的合作學(xué)習(xí)，教師要明確合作學(xué)習(xí)目標(biāo)，有的放矢實現(xiàn)學(xué)生高效合作，提高學(xué)生合作學(xué)習(xí)的能力.

1. 思考遇到困惑時，合作學(xué)習(xí)

學(xué)生在問題探討中常常會出現(xiàn)思維卡殼或者一知半解的情況，這時可以利用小組討論的方式引領(lǐng)學(xué)生合作學(xué)習(xí). 小組合作學(xué)習(xí)，同伴互助，相比于單一的教師講解，效果更好，影響更深.

案例5? 確定圓的條件.

學(xué)習(xí)三角形外接圓的知識后，教師設(shè)計以下問題：同學(xué)們想一想，能夠?qū)⒁粋€三角形完全覆蓋的最小的圓，一定是這個三角形的外接圓嗎？

生（齊）：是的. （未加驗證，直接回答）

師：老師準(zhǔn)備了一些紙質(zhì)圓片，大家通過小組合作的方式用這些圓片來驗證剛剛的猜想.

生（齊）：經(jīng)過驗證，我們發(fā)現(xiàn)了兩種情況. 第一種，假設(shè)三角形是銳角三角形或直角三角形，那么完全覆蓋三角形的最小的圓就是該三角形的外接圓. 第二種，假設(shè)三角形是鈍角三角形，那么完全覆蓋三角形的最小的圓不是它的外接圓，而是以其最長的邊為直徑的圓.

設(shè)計意圖？搖 本例中，當(dāng)學(xué)生的思維出現(xiàn)偏差時，教師及時通過合作學(xué)習(xí)的方式將學(xué)生的思維拉回到了正確的軌道上，獲得了正確的結(jié)論. 當(dāng)然教師要精準(zhǔn)把握介入時機(jī)，需要教師了解學(xué)生的思維水平，明確學(xué)生的思維盲點，而不是學(xué)生思考時一遇到困惑就立即開展合作學(xué)習(xí)，否則會使學(xué)生產(chǎn)生依賴性，錯失獨立思考的機(jī)會. 比如，若學(xué)生的困惑源于對問題的理解不夠清晰，則不適宜開展合作學(xué)習(xí)，教師通過講解更能使學(xué)生豁然開朗；若只是少數(shù)學(xué)生感到思維困惑，同樣不適宜開展合作學(xué)習(xí)，建議通過個別指導(dǎo)解除疑惑；若大部分學(xué)生都出現(xiàn)了思維障礙，而且遇到的問題具有合作探究的價值，則教師可抓住介入時機(jī)，鼓勵學(xué)生積極開展合作學(xué)習(xí).

2. 學(xué)習(xí)出現(xiàn)分歧時，合作學(xué)習(xí)

學(xué)生在知識探究過程中會由于理解不夠深刻和全面而出現(xiàn)認(rèn)識分歧的現(xiàn)象，此時需要教師積極組織學(xué)生合作討論，思考辨析，明辨是非，使學(xué)生形成正確的認(rèn)識.

案例6? “一元二次方程”的教學(xué).

講解完一元二次方程的概念后，學(xué)生僅僅從文字上理解了一元二次方程的概念，此時需要教師引導(dǎo)學(xué)生通過實際案例的辨析，抓住一元二次方程的本質(zhì)以深化認(rèn)識.

師：請同學(xué)們判斷下列哪些方程不是一元二次方程.

②（2x+1）（x－2）=2x2+3x－7；

③x2+3x－4=0；

④t2+2t+1=0；

⑤x2+8y+2=0.

學(xué)生討論方程①和方程②是否為一元二次方程時出現(xiàn)了思維分歧：有的學(xué)生化簡方程①后得到2x2－3x+1=0，認(rèn)為方程①是一元二次方程，這說明他們還沒有理解整式方程的概念；有的學(xué)生化簡方程②后得到其二次項系數(shù)為零，判斷方程②不是一元二次方程. 當(dāng)學(xué)生出現(xiàn)思維分歧時，教師及時組織學(xué)生進(jìn)行合作探究，讓學(xué)生在合作學(xué)習(xí)中形成更加深刻以及全面的認(rèn)識，提升學(xué)生的知識運用能力.

設(shè)計意圖? 本例中，面對學(xué)生理解不夠全面和一知半解的現(xiàn)象，以合作學(xué)習(xí)的方式展開探究，能夠找準(zhǔn)并消除學(xué)生的知識盲點，使學(xué)生思考更加便捷，減少了思考彎路，提高了學(xué)習(xí)效率，還提升了合作學(xué)習(xí)能力.

3. 提出有價值的問題時，合作學(xué)習(xí)

面對學(xué)生提出的各種問題，教師應(yīng)加以引導(dǎo)和分析，幫助學(xué)生篩選出有價值的問題，組織學(xué)生進(jìn)行合作探究，以此提高學(xué)生的合作能力.

案例7? “一次函數(shù)”的教學(xué).

問題：兩個一次函數(shù)的圖象關(guān)于x軸對稱，其中一個一次函數(shù)的解析式為y=x－3，求另一個一次函數(shù)的解析式.

生1：關(guān)于x軸對稱的兩個點的橫坐標(biāo)相同，縱坐標(biāo)互為相反數(shù)，是否可以直接得到所求一次函數(shù)的解析式為－y=x－3，即y=－x+3？

師：大家合作探究并思考生1的方法以及結(jié)論是否正確.

生2：我們在一次函數(shù)y=x－3的圖象上任意取一點P（t，t－3），可得其關(guān)于x軸的對稱點為Q（t，－t+3）. 令x=t，y=－t+3，可得y=－x+3.

生3：我們用一次函數(shù)的一般形式y(tǒng)=kx+b驗證生1的方法是正確的.

設(shè)計意圖? 通過合作學(xué)習(xí)激發(fā)學(xué)生思維的火花，發(fā)展學(xué)生的創(chuàng)新思維；從不同角度探索問題，驗證猜想，提升學(xué)生合作學(xué)習(xí)的能力.

綜上所述，合作學(xué)習(xí)是提高學(xué)習(xí)效率的一種有效方式.在教學(xué)中，教師要指導(dǎo)學(xué)生明確學(xué)習(xí)目標(biāo)，合理分工，認(rèn)真吸取他人的經(jīng)驗，不斷完善自我認(rèn)識. 合作學(xué)習(xí)是知識互相交流的過程，能夠?qū)崿F(xiàn)學(xué)生間的優(yōu)勢互補(bǔ)，因此教師要鼓勵學(xué)生提出自己獨特的觀點，與他人積極合作，從而全面提高數(shù)學(xué)能力.