拓展例題資源 優化思維品質

胡貴喜

［摘? 要］ 踐行“立德樹人”的教育理念是當前學科教育的大方向. 發揮例題資源的教育教學功能是優化學生思維品質，提升數學核心素養的重要舉措. 實踐證明，拓展例題背景，可降低問題的難度，豐富教學過程，有效提升思維的靈活性；變式拓展例題可揭露問題的本質，發展學生思維的深刻性；引申例題問題可增加知識的寬度與廣度，提升學生思維的創造性.

［關鍵詞］ 例題；拓展；思維品質

高品質的數學例題具有豐富的內涵，對發展學生的數學思維品質有著重要價值. 數學思維品質是指學生在數學學習過程中呈現出來的思維特征，它包含思維的靈活性、深刻性、廣闊性、批判性、創造性等. 教師若能有針對性地將一些例題進行拓展與延伸，則可進一步開闊學生的視野，優化學生的數學思維品質.

拓展例題背景，提升學生思維

的靈活性

數學是思維的體操. 教學中，我們常發現這樣一種現象：學生在小學時數學成績不錯，到初中階段之后明顯下滑，出現這種現象的主要原因在于前期的數學教育重點關注了學生對知識與技能的掌握情況，忽略了對學生數學思維品質的培養，導致學生思維靈活度欠缺，只能機械地模仿，無法自主靈活地解決更多問題.

現代教育心理學提出：思維是人類認知的核心組成部分，它的發展水平對學生的整個認知體系具有重要影響，尤其是思維靈活性的培養對學生的可持續性發展具有重要意義［1］. 究竟該如何借助例題拓展來靈活學生的數學思維呢？事實證明，拓展例題背景，往往能帶給學生耳目一新的感覺，或者帶領學生從不同的視角與途徑探尋同一個問題的結論，也能增強學生思維的靈活性.

例1 ？搖如圖1，已知△ABC為一直角三角形，已知△ABE和△DBC均為直角三角形，∠B為直角，BE=3 m，AE=DC=5 m，求當AD=EC時，AD=EC=_____m.

本題雖然難度不大，但比較枯燥，難以調動學生的解題興趣. 為了提升學生思維的靈活性，針對本題筆者將問題背景進行了拓展，將原題進行了如下改編：

如圖1，此為一根5 m長的梯子斜靠在與地面垂直的墻壁上，已知梯子下端與墻腳距離為3 m，若梯子底端向墻壁相反方向滑動的距離與頂端向下滑動的距離相等，那么梯子究竟滑動了多少米呢？

通過這個案例不難看出，在教學中拓展例題背景，一方面能將教學生活化，簡化問題的難度，深化學生對知識本質的理解；另一方面能幫助學生更好地提煉數學思想，讓學生學會從生活的角度思考與分析問題，提升思維的靈活度，為后續解決更多問題奠定方法基礎.

變式拓展例題，提升學生思維

的深刻性

例題的變式拓展在近年來應用得較多，尤其是《義務教育數學課程標準（2022年版）》明確提出要讓人人學有價值的數學，讓每個學生都能在數學學習中獲得不同程度的發展. 這一要求，讓教師更注重各個水平階層學生的思維發展程度. 例題的變式拓展一般是通過對問題條件或結論的變換，但問題的本質卻不發生改變，變式的應用為揭露知識本質服務.

變式拓展例題的主要目的就在于引導學生突破數學事物的表象，讓學生從全方位的視角來審視、觀察問題，并從知識間的聯系與矛盾中建構完整的知識結構［2］. 因此，變式拓展的應用從一定程度上可幫助學生消減思維惰性，增強學生思維的深刻性與廣闊性.

例2??如圖2，在△ABC中，已知∠B與∠C的角平分線相交于點O，∠A=100°，則∠BOC的度數是多少？

在學生順利解決此問之后，為了進一步深化學生對三角形內角和的認識，讓學生從根本上掌握這部分知識，筆者設計了如下變式：

變式1? 觀察圖2，在其他條件不變的情況下，求∠2+∠4的度數；

變式2? 結合圖2，在原題條件不變的情況下，說說∠BOC與∠2、∠4之間存在怎樣的關系？

變式3? 如圖2，在△ABC中，已知∠B與∠C的角平分線相交于點O，∠A=80°，則∠x的度數是多少？

變式4? 如圖2，在△ABC中，已知∠B與∠C的角平分線相交于點O，∠A=y°，則x，y之間具有怎樣的聯系？

變式拓展引申出一個個類似又有區別的問題，這些問題雖然呈現出來的形式各不一樣，但探索的知識本質卻沒有發生變化. 隨著變式問題的逐個突破，學生不僅在自我挑戰中獲得了學習的成就感，數學思維也隨著問題的逐漸深入拾級而上，這對促進學生思維的深刻性發展具有重要意義，也讓學生從教學中有所收獲.

鑒于不同認知水平層次的學生對知識的接受能力與理解能力有所差異，以上由淺入深的變式為學生的思維架起了橋梁，使得每個學生都從低起點開始思考，并在問題的逐漸深入中發現知識的本質. 因此，變式拓展例題不僅具有揭露知識本質，深化學生數學思維的重要作用，還能從真正意義上促進學生的差異化發展，這與新課標對例題教學所提出的要求一致.

引申例題問題，提升學生思維

的創造性

數學家波利亞提出，教學中，一個高質量的問題猶如野外生長的蘑菇，它們都是成堆地在一起，當你找到其中一個之后，極有可能在它的周圍發現更多個［3］. 例題教學通過對問題的拓展可培養學生的創新意識，讓學生形成堅忍的意志品質.

例題教學的問題拓展一般是從一個基本問題出發，借助聯想、類比、一般或特殊的數學思想方法，引導學生發現問題的發展與變化情況，探尋出問題本質的同時形成創新思維. 值得注意的是在此過程中，應注重克服思維定式的形成，只有帶領學生在變中求進，在進中求同，才能從真正意義上開拓學生思維的創新空間.

如借助典型例題由淺入深地設計階梯式的問題，可讓學生的思維經歷由淺入深的變化過程，從而對知識形成深刻理解，為創新服務.

原題：某港口位于東西向的海岸線，若甲乙兩艘輪船同時離開港口，分別沿著固定方向航行. 甲船每小時能行駛16海里，乙船每小時能行駛12海里，在它們離開港口1.5小時后，甲乙之間的距離是30海里，若明確甲船是向東北方向行駛的，那么乙船是朝向哪個方向行駛的呢？

在學生順利解決以上問題后，為了進一步提升學生思維的創造性，教師又提出如下幾個拓展性的問題：

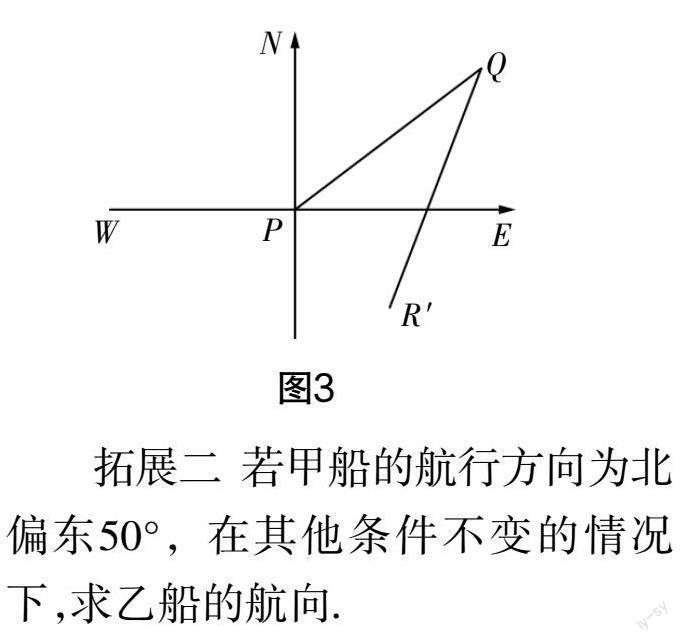
拓展一？搖 如圖3，乙船能向西南方向行駛嗎？

拓展二？搖 若甲船的航行方向為北偏東50°，在其他條件不變的情況下，求乙船的航向.

拓展三？搖 已知甲、乙兩艘船停泊在某海域上，兩條船同時離開停泊位置各自沿著一個固定方向行駛，已知甲船每小時可行駛16海里，乙船每小時可行駛12海里，1.5小時后，兩船之間的距離是30海里，若甲船是沿著北偏東60°的方向行駛，那么乙船的航行方向能確定嗎？

在原題的基礎上，第一個問題拓展幅度小，與學生的思維水平相匹配，具有思維熱身的作用. 第二個問題則在原題的基礎上增加了難度，這就需要學生積極開動腦筋，從多層次、多向性的交互思維中分析問題. 拓展三則需要學生克服在解題過程中形成的思維定式，創造性地解決問題，這也是促進創新思維形成的根本.

拓展例題資源，提升學生的思維品質還可以從其他方面實施，本文不再一一贅述. 綜上分析，不難看出充分利用好例題資源，并對其進行二次開發不僅能豐富課堂教學，還能讓學生從多維度思考與分析問題，促進思維靈活性、深刻性、創造性的發展.

參考文獻：

［1］周奕連. 有效拓展數學例題資源［J］. 中學教學參考，2018（26）：20-21.

［2］張繼海. 初中數學教材中例題、習題的演變方法［J］. 中國數學教育，2012（23）：34-40.

［3］G·波利亞. 怎樣解題——數學思維的新方法［M］. 涂私，馮承天，譯.上海：上海科技教育出版社，2007.