大概念引領 整體化建構

肖啟星

［摘? 要］ 初中數學的章起始課是數學教學中的重要課型. 研究者通過回顧一次函數學習活動經驗，引導學生類比思考，讓學生整體建構二次函數學習內容；同時以大概念為指導，幫助學生在二次函數知識建構的過程中形成數學思維方式，發展數學核心素養.

［關鍵詞］ 章起始課；大概念引領；整體化建構；二次函數

初中數學的章起始課是數學教學中的重要課型. 通過章起始課，學生可以整體感知整個章節內容，為后續學習奠定基礎. 同時，章起始課還提供了師生、生生互動交流的機會，讓學生體會章節的學習方法和策略，有助于培養學生的數學思維和解決問題的能力. 因此，重視并有效利用章起始課，對于提高初中數學教學質量和促進學生的全面發展具有重要意義.

2022年11月，筆者在廣東省教育科學研究院的安排下，錄制了廣東省中小學青年教師教學能力大賽一等獎優質教學資源課例——“二次函數”章起始課. 本節課的教學以“大概念引領，整體化建構”為立意，按照先行組織、類比思考、整體建構的思路展開. 接下來，筆者將闡述這節課的教學實踐與教學思考.

內容分析

本節課是北師大版九年級下冊第二章第一節“二次函數”的內容. 二次函數是初中數學的重要內容之一，它是學生學習代數式、方程、一次函數、反比例函數后的綜合學習內容. 二次函數的學習不僅強化了學生對函數概念、圖象、性質、應用、研究方法等進一步的理解掌握，同時也為高中繼續學習其他函數和一元二次不等式奠定了基礎.

學情分析

學生已經經歷了一些解決實際問題的活動，會從實際問題中抽象出一次函數和反比例函數的概念，并會用列表、圖象、解析式三種方法研究函數，以及掌握了所學函數的表達式、圖象及其性質，為學習二次函數新知識打下了基礎. 同時在以前的數學學習活動中也積累了一定的合作交流經驗，具備了一定的自主探究的能力.

目標設置

1. 在實際問題中建立變量間的二次函數關系，感悟其中的模型觀念.

2. 通過類比一次函數形成二次函數的研究方法，對本章內容形成結構化和整體性認識，提升自主建構知識的能力.

3. 體會數形結合思想，培養抽象能力，發展幾何直觀.

重點難點

基于以上教學內容和學情分析，本節課以章起始課引領二次函數定義的學習，確定教學重難點.

教學重點：根據實際問題建立二次函數模型；研究二次函數的基本思路.

教學難點：從實際問題中建立二次函數的表達式.

教學實踐

本節課從以下5個教學環節展開：回顧舊知，引入概念；歸納類比，形成概念；應用新知，辨析概念；拓展提升，鞏固新知；總結思考，內化升華.

環節1：回顧舊知，引入概念.

問題1：大家有沒有留意過噴泉水流經過的路線？觀看籃球比賽時你是否留意過籃球入網的路線？它們會與某種函數有聯系嗎？這就是本章要學習的內容.

設計意圖? 通過講解章引言和章頭圖，設疑引趣，喚起學生的求知欲. 同時明確本章的學習目標，為學生學習整個章節的知識起一個統領性的作用.

問題2：展示五個情境，學生思考.

情境1：在本月體育測試中，初三女生進行了長跑練習，平均速度為300 m/min.? 假設練習時間為t（min），女生跑的路程為s（m），那么s與t之間的函數關系式是什么？

情境2：小勤同學買了一本中考英語詞匯書，該書共有4000個單詞，假設她計劃用y天掌握全部單詞，平均每天需掌握的單詞數為 x（個），那么 y 與 x 之間的函數關系式是什么？

情境3：用總長為20 ｍ的籬笆，一面靠墻，圍成一個矩形的花圃. 設矩形垂直于墻的一邊長為x ｍ，矩形的面積y ｍ2，y與x之間的函數關系式是什么？

情境4：隨著中考臨近，初三某畢業班的每個同學都向其他同學贈送一張自己的照片留作紀念. 若學生有x人（x≥2），他們互相贈送的照片總數為y張. y與x之間的函數關系式是什么？

情境5：某商場銷售一批衣服，每件進價40元，據市場分析，若按每件60元銷售，平均每天可售出10件. 經調查發現，在一定范圍內，衣服單價每降1元，商場平均可多售出2件. 若每件衣服降價x元，商場銷售此種衣服的數量為y件，銷售此種衣服的總利潤為w元. y與x之間的函數關系式是什么？w與x之間的函數關系式是什么？

設計意圖? 從生活實際出發，學生自主發現兩個變量之間具有某種數量關系，讓學生感知函數的價值. 書寫函數表達式的過程，就是將生活問題數學化的過程，進一步培養學生的模型觀念.

學生思考獲得以下函數表達式：（1）s=300t；（2）y=；（3）y= -2x2+20x；（4）y=x2-x；（5）y=10+2x，w=-2x2+30x+200.

問題3：其中有你熟悉的函數嗎？我們是從哪些方面研究這些函數的？

設計意圖? 通過對一次函數的定義、圖象、性質、應用的復習，喚醒學生已有的研究函數的基本范式，為后續研究二次函數做好鋪墊.

環節2：歸納類比，形成概念.

問題4：（3）（4）及（5）中第二個函數這三個函數表達式有什么共同特征，你覺得叫什么名字合適？類比一次函數你能否歸納這類函數的定義？

學生通過對一次函數的觀察和類比，能夠得到這三個函數的共同特點：它們是關于自變量的二次多項式. 由此可以得到二次函數的定義：兩個變量x，y之間的對應關系可以表示成y=ax2+bx+c（a，b，c是常數，a≠0）的形式，稱y是x的二次函數. a，b，c分別叫作二次項系數、一次項系數、常數項.

設計意圖? 觀察到三個表達式的共同特征都是含有自變量的二次項. 學生通過類比一次函數的命名來對這三個函數表達式進行命名，在新知識與舊知識的對比中，教師引導學生歸納出二次函數的概念和表達式，從而培養他們的抽象能力.

環節3：應用新知，辨析概念.

練習1：下列各式中，y是x的二次函數嗎？如果是，請指出各項系數a，b，c是多少；如果不是，請說明理由.

設計意圖? 通過交流分享，概念辨析，加深學生對二次函數概念的理解. 在對各項系數辨析的過程中，強化學生的符號意識，發展其模型觀念.

問題5：請同學們嘗試在生活中或熟悉的數學問題中尋找二次函數的實例.

學生根據上一章一元二次方程所學和生活實踐體會提出：圓的面積與半徑之間的關系、自由落體物體下落的高度與時間的關系、握手問題、增長率問題等都有二次函數的實例.

設計意圖? 通過尋找生活中二次函數模型并列出二次函數的關系，進一步發展學生的模型觀念. 通過感知二次函數與一元二次方程的關系，為學生今后學習二次函數的應用奠定基礎.

環節4：拓展提升，鞏固新知.

練習2：用總長為20 ｍ的籬笆，一面靠墻，圍成一個矩形的花圃. 設矩形垂直于墻的一邊AB的長為x ｍ，矩形的面積為y ｍ2．（1）求y與x之間的關系式和變量x的取值范圍. （2）當x取2 m、4 m、6 m、8 m時，相應的y值分別是多少？（3）你還能提出什么問題？

在“你還能提出什么問題”這個環節中，學生有如下問題：

①AB邊為多長時，花圃的面積為49？

師：你是怎樣想到這個問題的？

生：之前一直都是已知x去求y，我想反過來. （培養學生逆向思維）

師：如何解決這個問題？

生：可以通過建立一元二次方程求解. （學生進一步感知二次函數與一元二次方程的關系）

②AB邊為多長時，花圃的面積最大？

師：你是怎樣想到這個問題的？

生：x取2 m、4 m、6 m、8 m時，y的值都不一樣，我猜測能否有最大值.

師：如何解決這個問題？

生：多給一些數據. （學生從特殊到一般去思考問題，發展抽象素養）

設計意圖? 學生通過編題，更加清晰地了解條件和結論的關系，能充分感知二次函數作為一個模型的主要作用是描述現實問題中的數量關系.

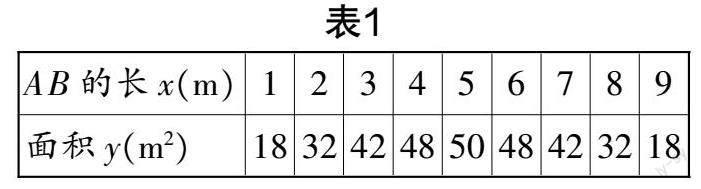
練習3：試填表（見表1），并觀察表格，你發現了什么？

學生通過自主描點、連線觀察，初步感知二次函數圖象為曲線，教師順勢提出了二次函數的圖象是拋物線的概念. 進一步觀察圖象，學生會發現隨著x的增大，y先增大再變小. 教師適時引導學生思考：這個二次函數的圖象還有什么樣的性質？學生通過合作交流歸納出二次函數的開口方向、增減性、對稱性、最值性等，學習了數形結合思想，發展了模型觀念.

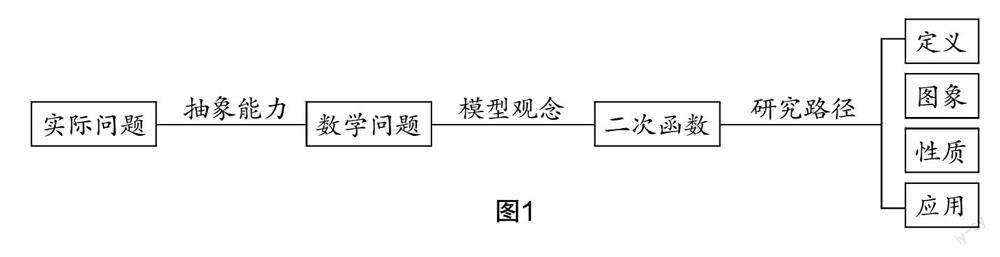
設計意圖? 探究“何時矩形的面積最大”的問題中，教師讓學生用列表、圖象、解析式三種方法去研究函數的最值的問題，為學生進一步學習二次函數的圖象和性質打好基礎. 這也體現了研究二次函數的路徑：定義、圖象、性質、應用. 通過構建二次函數單元的整體框架，有效幫助學生整體把握單元學習的主干知識，較好地體現了單元整體的教學理念.

環節5：總結思考，內化升華.

問題6：（1）本節課我們學習了什么？我們是怎么得到二次函數的？（2）我們從哪些方面研究函數？后續我們將學習二次函數的哪些知識？

設計意圖? 學生經過教師點撥、自主探究與合作交流，實現了知識的類比遷移，總結出了二次函數與之前所接觸的函數同樣遵循一定的研究路徑：先把函數的概念通過具體的事例中抽象出來，再對函數的圖象及性質進行探究，最后用函數的概念和性質解決實際問題. 給出二次函數的整體框架圖，為后續的課堂教學提供明確的方向.

作業布置：

（基礎性作業）隨堂練習第1題，習題2.1第1題；

（拓展性作業）對于函數表達式y=3x3+1你可以給它命名嗎？并說說你打算如何研究它？

設計意圖? 通過拓展性作業，讓學生對函數的學習內容、研究方法、應用價值有更深層次的理解，從而類比探索未知函數y=3x3+1，發展遷移能力. 學生在高中學習指數函數、冪函數、三角函數等知識時，知道從概念、圖象、性質、應用這些角度去研究.

教學思考

1. 重視大概念引領，凸顯函數本質意義

通過對教材和課程標準進行研究，對具有相同的知識結構、研究路徑、思想方法的教學內容進行梳理，提煉出大概念. 在大概念的引領下，教學內容由相同的研究路徑加以支撐，從而形成體現數學學科本質，能發展學生未來學習力的結構化知識體系.

筆者對“函數是研究客觀事物變化規律的重要模型”這一大概念進行提煉，通過具體實例讓學生感受豐富的函數問題背景，體驗一次函數與二次函數的區別和聯系. 學生在類比的學習過程中，對“函數”大概念有進一步的深入理解和掌握，從而更好地理解函數的本質，掌握函數的思想和方法，提高函數的應用能力.

2. 滲透整體化建構，重視單元整體教學

在初中階段，學生通過學習一次函數、反比例函數和二次函數等單元，深入理解了函數的概念及其在實際問題中的應用. 因此，初中函數的學習需要注重整體性和結構性，幫助學生建立完整的函數知識體系，為學生進一步學習數學和其他學科打下堅實的基礎.

筆者把比較宏觀的單元整體教學微縮到章起始課教學中，用單元整體教學的結構、思路、方式，處理章起始課的課時教學. 在章起始課中，筆者既揭示了二次函數單元的知識架構，又突出了本單元的核心問題，還滲透了本單元所需要的數學思想方法.

3. 注重思維的訓練，發展學生核心素養

課程目標以學生發展為本，以核心素養為導向. 核心素養是數學學習的關鍵，它有助于培養學生的思維能力，提高學生解決問題的能力.

筆者在教學二次函數時，通過實例引入二次函數的概念，讓學生從實際情境中抽象出數學模型，培養抽象能力；通過探究矩形面積問題的實際情境，讓學生進一步感受二次函數的模型，并理解如何運用二次函數模型解決實際問題，培養模型觀念；通過列表、描點、作圖，進一步體會二次函數表達式和函數圖象的相互轉換，感知數形結合思想.