快壓縮P1波在飽和凍土與彈性基巖分界面上的能量傳輸特性
馬 強, 蔣匯鵬, 周鳳璽, 蔣寧山
(1. 青海大學 土木工程學院, 西寧 810016;2. 青海省建筑節能材料與工程安全重點實驗室, 西寧 810016;3. 蘭州理工大學 土木工程學院, 蘭州 730050)
我國的凍土分布較廣且多集中在高海拔高寒地區,隨著國家“一帶一路”戰略推進,西部高寒地區的基礎建設不斷完善。然而,眾多工程(即水壩、橋梁和鐵路)建立在凍土層之上,凍土層的地震反應和波的傳播與未凍土存在明顯差異,一定程度上加大了工程建設及檢測的難度[1]。地震可以分為天然地震和人工地震,不同于天然地震的人工震源、地震勘探和人工爆破中主要激發產生壓縮波,此類波的傳播速度極快且衰減系數較小。因此,凍土場地中由人工震源產生的壓縮波響應在建筑設計和建筑安全中起著重要作用。通常高寒地區的工程結構是建立在凍土和巖石上,而選用飽和凍土與彈性基巖分界面上的透反射模型更貼近實際工程情況,能夠模擬飽和凍土與寒冷地區地下幾公里處的基巖接觸,那里的溫度非常低,基巖可以被認為是一種彈性介質。本文模擬的地震波入射為人工震源,選取傳播速度在飽和凍土中最大的快壓縮P1波,其在地震勘探、地基隔振效果評估、海底沉積物中天然氣水合物儲量評估、冷凍食品超聲無損檢測等領域有實際應用,根據它們對波的傳播特性(如傳播時間、波速、波幅和波的傳播能量)的反應進行分析。因此,通過分析快壓縮P1波在飽和凍土與彈性基巖分界面上的能量傳輸特性,為研究人員和現場工程師提供了重要的信息。
飽和凍土與彈性基巖分界面上P1波的能量傳輸特性涉及兩個關鍵問題:一是飽和凍土多孔多相介質的物理力學描述;二是飽和凍土與彈性基巖分界面上的入射波能量分配問題。對于第一個關鍵問題,凍結飽和多孔介質被認為是由土顆粒形成的復合固體骨架和孔隙組成,孔隙中充滿水和冰。因此,存在兩種固相基體(土體基體和冰基體),一般情況下,土體和冰顆粒之間存在相互作用;隨著溫度的降低,膠結作用逐漸增強。此外,由于冰和水之間的相互轉化,在凍土中形成了復雜的多相結構[2]。即使孔隙中充滿水,凍土仍然是固相、冰相和液相的三相復合體,并有相變。因此,凍土的物理模型一直是一個復雜而困難的問題。在過去幾十年的研究中,許多學者致力于研究和建立各種凍土多孔介質模型來描述凍土的物理力學性質,并取得了豐碩的成果[3-5]。然而,目前僅有少數幾種模型適用于飽和凍土的傳播特性分析。Leclaire等[6]建立了由土骨架、冰顆粒、液態水三相組成的凍結飽和多孔介質的運動學LCA模型,但忽略了土體與冰相的相互作用。隨后通過試驗,基于所建立的凍結飽和多孔介質模型進行超聲測試,驗證了模型預測的多重體波存在[7]。Carcione進一步考慮了土骨架與冰顆粒、液態水三相之間的相互作用,提出了一個更為嚴格的LCAM模型[8-10]。周鳳璽等[11]應用混合理論,建立了飽和凍土介質彈性波的彌散方程,并給出了飽和凍土中彈性波傳播速度和衰減系數的解析表達式,但他假設土骨架和孔隙冰的速度和位移相等,因此僅得到2種壓縮波和1種剪切波。仇浩淼等[12]基于Leclaire理論,研究了飽和凍土中體波相速度及飽和度、衰減系數、孔隙率等參數之間的關系。Cao等[13]和Li等[14]分別應用Leclaire建立的LCA模型和Carcione建立的LCAM模型,研究了沖擊荷載作用下凍土中樁的豎向動力響應。周斌[15]分別應用LCA模型和LCAM模型,研究了在溫度影響下凍土地區地基表面地震動和Rayleigh波的傳播特性。第二個關鍵問題是飽和凍土與彈性基巖分界面上的入射波能量分配問題,現有文獻主要集中在飽和多孔介質/非飽和多孔介質分界面上的能量傳輸特性[16-17],然而飽和凍土分界面上的能量分配問題卻極少被考慮。彈性固體表現為非耗散性,而飽和凍土由于孔隙流體中存在粘性,對波傳播表現為耗散性[18]。彈性基巖中的所有波(即透射波)都是均勻的(即傳播和衰減方向相同),而飽和凍土中的所有入射波和反射波都是不均勻的(即傳播和衰減方向不同)。 因此,對于給定的入射波,透反射振幅比是一個非奇異線性方程組,以能量矩陣的形式得到透反射波的能量份額[19]。通過數值算例解出入射能量在各種透反射波之間的分配。從入射頻率、溫度(含冰量)、孔隙率和膠結參數和接觸參數等方面分析了入射方向對入射能量分配的影響。
本文構建的模型中,彈性基巖中存在兩種體波,分別是壓縮波和剪切波均是由固體基巖產生。在飽和凍土中壓縮波和剪切波的產生與土骨架、孔隙水和孔隙冰三相相關,壓縮波(P1和P2波)與剪切波(S1波)的傳播性質類似飽和多孔介質中的快壓縮波(P1波)和慢壓縮波(P2波)和土骨架產生的剪切波(S波)。P1波是土骨架與孔隙水同時壓縮產生的波,即“同相波”、P2波是土骨架松弛而孔隙水壓縮產生的波,即“異相波”、P3波的出現是由于飽和凍土中存在第三相孔隙冰介質和孔隙水作用的結果。當未凍水逐漸凝化成冰時,冰在孔隙中形成,并擠出部分孔隙水,此時由于孔隙冰的存在,會產生另外一種慢壓縮波(P3波)和剪切波(S2波)。目前,關于飽和凍土與其他介質(例如彈性介質,飽和多孔彈性介質,非飽和多孔彈性介質)分界面處彈性波的透射和反射特性研究極少。彈性波在分界面處的透射和反射問題是土動力學研究中一個重要的目標。迄今為止,多孔彈性介質中彈性波傳播的研究已有幾十年的歷史[20-23]。以往彈性波在分界面處的透反射性質研究主要集中在單相彈性介質/飽和土介質分界面[24-26],單相彈性介質/非飽和土介質分界面[27],飽和土介質/飽和土介質分界面[28-30]以及非飽和土介質/非飽和土介質分界面[31-33]。僅有仇浩淼[34]對理想流體/含孔隙固體多孔介質界面處的透反射性質進行了研究。
本文基于彈性波在凍結飽和多孔介質和單相彈性介質中的傳播理論,建立了從飽和凍土入射到彈性基巖分界面處的P1波的透反射模型。本文的主要研究是:首先,利用Helmholtz矢量分解原理,結合分界面上的邊界條件推導獲得了P1波在分界面上的透反射振幅比的理論表達式。然后,根據分界面處單位面積上透反射波的能量分配定義,結合透反射振幅比進一步求解出各類波能量率的理論表達式。最后,分析了當P1波從飽和凍土入射到彈性基巖分界面時,能量比例系數(即能量透反射率和能量相互作用率)與入射角度,入射頻率,溫度(含冰量),孔隙率,膠結參數和接觸參數之間的變化關系。
1 飽和凍土的波動理論
1.1 孔隙含冰量與溫度的關系
飽和凍土的理論模型中物理參數較多,Leclaire等和Carcione等明確闡明了這些參數之間的內在聯系。飽和凍土的孔隙率和含冰量是評價飽和凍土物理力學性能的重要參數。飽和凍土的孔隙率可由三相比例關系確定,而孔隙中未凍水含量的準確測定相對繁瑣。本文采用大寫字母“S”,“F”和“I”分別表示飽和凍土介質中的土骨架,孔隙流體(未凍水)和冰顆粒的成分。將使用上標α來表示材料和場變量(其中α= S,F,I),nα表示α相介質的體積分數。基本關系列示如下
nS+nF+nI=1,nF+nI=φ
(1)
式中:φ為包括未凍水和冰的總水比例,稱為孔隙率;nS、nF和nI分別為土骨架、未凍水和冰的體積比例(為方便描述,本文稱nI為含冰量)。
孔隙中冰顆粒的含量取決于溫度和孔隙的分布,本文根據Carcione等進一步給出了如下關系式
(2)
(3)
(4)
式中:Tk= (Tk0+T)以開爾文為單位,Tk0= 273.15 K,T表示溫度以攝氏度為單位;r0、rav和Δr分別為飽和凍土中的毛細孔徑、毛細孔徑平均半徑和毛細孔徑標準差(Leclaire等)。
1.2 飽和凍土的波動方程
本文的飽和凍土用飽和凍結多孔彈性介質模擬,Carcione等給出了飽和凍土介質的本構方程和運動方程為
(1) 本構方程
(5)
σF=-nFPF=C12θS+K2θF+C23θI
(6)
(7)
(2) 運動方程

(8)
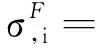
(9)
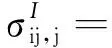
(10)
(3) 飽和凍土中三相介質的體應變、偏應變和應變分別表示為
(11)
(12)
(13)

Carcione等在Leclaire等理論的基礎上,為飽和凍土建立了以下的波動方程

(14)

(15)
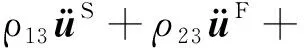
(16)
式中:矢量的相乘有兩種定義,?·是標量積(點乘積),?×是矢量積(叉乘積);▽2為笛卡爾坐標系中的Laplace算子;ρα表示α相介質的密度;Rij(i=1,2,3;j=1,2,3)為剛度參數;上述中的參數見附錄A。
基于Helmholtz矢量分解定理將飽和凍土中土相、液相和冰相的位移矢量分解為
uS=?ψS+?×HS
(17)
uF=?ψF+?×HF
(18)
uI=?ψI+?×HI
(19)
式中,ψα和Hα(α=S,F,I)分別表示為飽和凍土中土骨架、孔隙流體和冰顆粒介質的標量和矢量勢函數。
將式(17)~(19)代入波動方程(14)和(15)中,則波動方程可進一步表示為

(20)

(21)

(22)
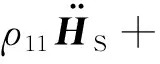
(23)
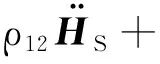
(24)

(25)
解的一般形式為
(26)
(27)

將式(26)和(27)代入式(20)~(25)中,經過推導可以得到控制壓縮波和剪切波振幅分量的線性方程組為
(28)
(29)
式中,元素aij和cij(i=1,2,3;j=1,2,3),在附錄A中給出。
因式(28)和(29)具有非零解,可以推導出壓縮波和剪切波的特征方程為
(30)
(31)
通過求解特征方程(30)和(31),可以得到飽和凍土中P波和S波的傳播相速度為
cj=ω/Re(kj)
(32)
式中,Re表示復數實部的運算符。特征方程(30)在j=P1、P2、P3中的解有3個根,對應于飽和凍土介質中的P1、P2、P3壓縮波。特征方程(31)在j=S1、S2中的解有2個根,對應于飽和凍土介質中的S1、S2剪切波。且5種體波是色散的,這意味著相速度和頻率相關。
基于本文所考慮的研究參數取值,通過MATLAB編程軟件將特征方程(30)和(31)進行求解,得到飽和凍土中各類波的速度范圍如表1所示。

表1 飽和凍土中彈性波的波速范圍Tab.1 Velocity range of elastic waves in saturated frozen soil 單位:m/s
2 快壓縮P1波在分界面上的透射與反射
如圖1所示,快壓縮P1波從飽和凍土介質入射到彈性基巖分界面上的透射與反射模型。飽和凍土介質占據z<0的區域,彈性基巖占據z>0的區域,z= 0對應于兩個半空間的接觸界面。假設快壓縮P1波以任意角度θip1從飽和凍土介質射向彈性基巖,在彈性基巖與飽和凍土介質分界面處將產生出2種透射波(透射P波,透射S波),5種反射波(反射P1波,反射P2波,反射P3波,反射S1波和反射S2波)。波動被限制在x-z平面中,所有的量與y坐標無關,界面單位矢量在z方向。

圖1 入射快壓縮P1波在飽和凍土與彈性基巖分界面上的反射波與透射波示意圖Fig.1 The reflected and transmitted waves schematic of an incident fast compressional P1-wave at the interface between saturated frozen soil and elastic bedrock
2.1 波的勢函數
入射和透反射波的位移勢函數表示如下
對于飽和凍土介質部分(z<0)
(1) 入射P1波的勢函數
(33)
(2) 反射P波的勢函數
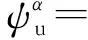
(34)
(3) 反射S波的勢函數
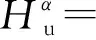
(35)
對于彈性基巖部分(z>0)
(4) 透射P波的勢函數
ψe=Atpexp[iktp(ltpx+ntpz-ctpt)]
(36)
(5) 透射S波的勢函數
He=Btsexp[ikts(ltsx+ntsz-ctst)]
(37)

2.2 分界面上的邊界條件
在分界面處透反射問題的邊界條件應當明確表示。Tajuddin等[35-36]基于Biot理論中的邊界條件提出了含孔隙固體多孔介質中的邊界條件,研究了孔隙固體與骨架間存在耦合作用的邊界條件以及不存在耦合作用的邊界條件。結果表明,當含孔隙固體多孔介質的計算參數相同時,兩種邊界條件幾乎沒有差異。Qiu等[37]基于Tajuddin提出的邊界條件,假設兩固相間的位移協調,且考慮了孔隙固體與骨架間的耦合作用,分析了P1波與S1波在含孔隙固體多孔介質自由邊界上的反射問題。本文與Qiu在分界面上的假設一致,因此單相彈性基巖與飽和凍土介質的分界面上的邊界條件如下所示
分界面上法向總應力連續:
(38)
分界面上切向總應力連續:
(39)
土骨架與孔隙冰,兩固相之間的法向和切向位移連續:
(40)
(41)
分界面上法向和切向位移連續:
(42)
(43)
對于不透水分界面,孔隙流體與固體骨架之間沒有相對運動,分界面上法向位移連續:
(44)
2.3 透反射振幅比
將式(5)~(7)、(11)~(13)代入式(38)~(44)中可得出用勢函數表達的邊界條件為

(45)

(46)
(47)
(48)
(49)
(50)
(51)
根據Snell定理,入射波和透反射波之間的角度和波數存在以下關系
lip1kip1=ltpktp=ltskts=lrp1krp1=lrp2krp2=lrp3krp3=lrs1krs1=lrs2krs2
(52)
將式(33)~(37)代入邊界條件(45)~(51)中,結合Snell定律式(52),可以得出下列的矩陣關系式
(53)
式中,矩陣m11~m77和q1~q7的系數在附錄B中給出。
透射波和反射波的透射振幅比和反射振幅比可以表示為
(54)
式中:Rrp1、Rrp2、Rrp3、Rrs1、Rrs2分別為反射P1波、反射P2波、反射P3波、反射S1波和反射S2波的反射振幅比;Rtp和Rts分別為透射P波和透射S波的透射振幅比。
3 透射波與反射波的能量率
本文主要研究入射P1波的能量在飽和凍土與彈性基巖分界面(z=0)單位面積上各類透射波與反射波能量的分布。根據Kumar等[38-40]研究的結果,通過單位面積上的能量可以用表面牽引力和粒子速度的標量積來表示。現分析入射P1波攜帶的能量在界面z=0處的分配情況,按照仇浩淼仿照飽和多孔介質中坡印廷矢量在z方向上的定義,入射P1波引起坡印廷矢量在z方向上的分量可以寫為一個周期內單位面積上的應力在z方向上分量與速度在z方向上分量的標量積,即單位面積上的時間平均能流函數為
(55)

(56)
式中:Eez和Euz分別表示彈性基巖中透射波與飽和凍土介質中入射波和反射波的能流密度在一個周期內的平均值;T= 2π/ω為入射波的周期。
對于一般的場變量A、B,在一個周期內的平均值有如下關系
(57)
式中,上標*表示復數B的共軛。
因此,入射波、反射波和透射波的平均能流密度可以寫為
(58)

(59)
為得到各透射波、反射波和入射波的能量率,將式(58)和(59)改寫為下列矩陣方程
(60)

(61)
(62)
(63)
(64)
(65)
通過將透反射波的能流密度依次除以入射P1波的能流密度,即可得出該波的能量比系數(即能量反射率與能量透射率),從而各種波的能量透射率和能量反射率為
(66)
其中

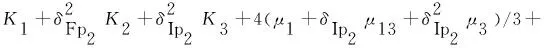


式中:etp和ets分別為透射P和S波的能量透射率;erp1、erp2、erp3、ers1和ers2分別為反射P1、P2、P3、S1和S2的能量反射率。
由于彈性基巖表現為非耗散性,而飽和凍土介質由于孔隙流體和孔隙冰的存在表現為耗散性,結果表現為透射波均勻,而反射波不均勻,飽和凍土中各類波之間相互作用的能量率為
(67)
式中:i、j=1,2,3,4,5,6;Eij為飽和凍土中第i種波產生的應力與第j種波產生的速度作用形成的能流密度;i=j表示為各種波能流密度;i≠j表示為不同波之間相互作用產生的能流密度;emix表示為相互作用下波的能量相互作用率。
由于考慮了入射波攜帶的能量在整個反射和透射過程中的消散程度,因此根據能量守恒需滿足在彈性基巖與飽和凍土介質自由表面上(z= 0)各反射波和透射波的能量率如下所示
(68)
式中,esum為所有透反射波的能量率之和。
4 數值驗證與分析
4.1 數值驗證
Kumar等研究了入射角對飽和凍土自由表面處反射波振幅比的影響,在基本假定中忽略其溫度效應的影響。為了驗證本文研究的正確性,本文將飽和凍土模型退化為不考慮溫度的情況,求解了飽和凍土自由表面處的反射波振幅比與入射角之間的關系,并與文獻中得到的結果進行了對比。驗證計算采用了與上述文獻相同的物理參數和邊界條件(文獻中的參數是 Lee 和 Waite 對加拿大西部 Mallik 5L-38 永久凍土氣體水合物研究井給出的值),如表2和表3所示。

表2 驗證的計算參數Tab.2 Calculated parameters for validation

表3 驗證的邊界條件Tab.3 Boundary conditions for validation
圖2給出了飽和凍土在自由邊界處的三個壓縮波和兩個剪切波的反射振幅比與入射角之間的關系。由圖2可知,本文的求解與文獻的求解計算結果相同,這進一步說明了本文方法的正確性。然后,通過數值計算研究了P1波從飽和凍土到彈性固體基巖分界面上的能量傳輸特性。

(a) 反射P1波

(b) 反射P2波

(c) 反射P3波

(d) 反射S1波

(e) 反射S2波圖2 本文解與文獻解的對比驗證Fig.2 Comparison between present work and analytical solution
本節通過數值計算,研究了快壓縮P1波從飽和凍土入射到彈性基巖分界面上的能量傳輸問題,具體分析了能量透反射率與能量相互作用率在不同入射頻率f、溫度T(含冰量nI)、孔隙率φ、膠結參數α和接觸參數ε條件下隨入射角度θip1變化的關系。其中飽和凍土介質與彈性基巖的計算參數在表4中詳細給出。

表4 飽和凍土介質與彈性基巖的計算參數Tab.4 Calculation parameters for saturated frozen soil medium and elastic bedrock
4.2 入射頻率對透反射波能量率的影響
當入射P1波從飽和凍土介質入射到彈性基巖時,存在臨界角度θcr,取孔隙率φ= 0.3,接觸參數ε= 0.5,溫度T= -0.50 ℃(含冰量nI=0.192),泊松比v= 0.35,入射頻率f為10、100和1 000 Hz,彈性基巖的剪切模量μe= 8 GPa,拉梅常量λe= 12 GPa,彈性基巖的密度為ρe= 2 700 kg/m3,其他計算參數見表4,在彈性基巖中,剪切波和壓縮波的速度基于彈性波動力學解得
(69)
(70)
由表1所知,飽和凍土中反射P1波的相速度約為2 400~3 150 m/s,因此飽和凍土中入射P1波的波速小于彈性基巖中透射P波的波速,計算出透射P波的臨界角度為:θcr=arcsin(cip1/ctp)≈50°~80°,因此彈性基巖中透射P波的透射角大于入射P1波的入射角。當入射角θip1增大到一定程度但還沒達到90°,透射P波的透射角超過90°,此時透射P波在彈性基巖中沿界面“滑行”,出現了“全反射”現象,伴隨著透射P波消失,此時的入射角度,即為本文的臨界角θcr。
如圖3所示,在不同頻率條件下,各種波的能量反射率,能量透射率和相互作用下波的能量相互作用率(本文用emix波表示相互作用下的波)隨入射角的變化曲線。從圖3(a)~(h)中可以看出,頻率對反射P2、P3和S2波的能量反射率影響較大,而對透射P、S波與反射P1、S1波和emix波的能量透反射率和能量相互作用率影響較小。造成這一結果的原因是由飽和凍土中五種體波的波速受頻率的影響變化較小,即波速的大小也間接影響能量率的分配與變化。其中反射P2、P3和S2波的能量反射率隨頻率的增加而顯著增大,而透射P、S波與反射P1、S1波和emix波的能量透反射率和能量相互作用率幾乎不受到頻率的影響。對比圖3(a)~(h)可知,透射P波、反射P1波和emix波的能量透反射率和能量相互作用率處于同一數量級,要比反射P2、P3和S2波的能量反射率大好幾個數量級。

(a) 透射P波

(b) 透射S波

(c) 反射P1波

(d) 反射P2波

(e) 反射P3波

(f) 反射S1波

(g) 反射S2波

(h) 相互作用波圖3 不同頻率下透反射波能量率隨入射角的變化曲線Fig.3 The energy ratio curve of transmitted and reflected waves with the incident angle under different frequencies
另一方面,從圖3(a)~(h)我們可以發現,當入射P1波垂直入射(即θip1= 0°)到分界面上時,沒有透射S波與反射S1和S2波產生,即不產生剪切波,此時僅有透射P波和反射P1、P2和P3波存在且透射P波的能量透射率最大,能量相互作用率最低。當達到臨界角時,各類波出現明顯的脈沖峰值或波谷,透射P波的能量透射率將降低到0,隨后透射P波消失,emix波的能量相互作用率達到峰值,此時分界面上的能量耗散達到最大。當掠入射時(即θip1= 90°)反射P1波幾乎占據全部的能量,其余波的能量急劇下降。
4.3 溫度(含冰量)對透反射波能量率的影響
含冰量和溫度是反映凍土性質的兩個重要指標,且含冰量隨溫度的變化而變化。當飽和凍土中溫度下降時,未凍水凝固成冰,在本文方程(2)中給出了含冰量和溫度的關系式,為探究溫度(含冰量)對透反射波能量率的影響,進行如下分析。
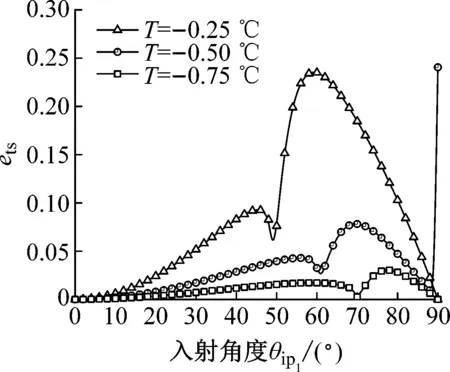
取入射頻率f= 100 Hz,孔隙率φ= 0.4,泊松比v= 0.35,接觸參數ε= 0.5,溫度T= -0.25 ℃、-0.50 ℃和-0.75 ℃。當溫度T= -0.25 ℃時,含冰量很低nI=0.032,未凍水幾乎充滿孔隙nF=0.368;溫度T= -0.50 ℃,含冰量nI=0.192,未凍水含量nF=0.208;溫度T= -0.75 ℃,含冰量nI=0.270,未凍水含量nF=0.130。隨著溫度的降低(含冰量的增加),臨界角越晚出現。溫度T的變化對透射S波和反射P1、P2、P3和S1波具有相同的影響,它們的能量透反射率隨溫度的降低而單調遞減。相反,對于透射P波和emix波的能量透射率和能量相互作用率隨著溫度T的降低而增加。隨著溫度的降低,反射P1波的脈沖峰值越大。從圖4(g)可以看出,在含冰量nI=0.032和nI=0.270下,反射S2波的能量反射率均明顯小于含冰量nI=0.192時,說明冰顆粒主導著透射S2波的產生,且在較高含冰量和較低含冰量時對透射S2波的能量起衰減作用。值得注意的是,溫度對波速的影響較大,對其能量率的影響也越大。

(a) 透射P波
(b) 透射S波

(c) 反射P1波

(d) 反射P2波

(e) 反射P3波

(f) 反射S1波

(g) 反射S2波
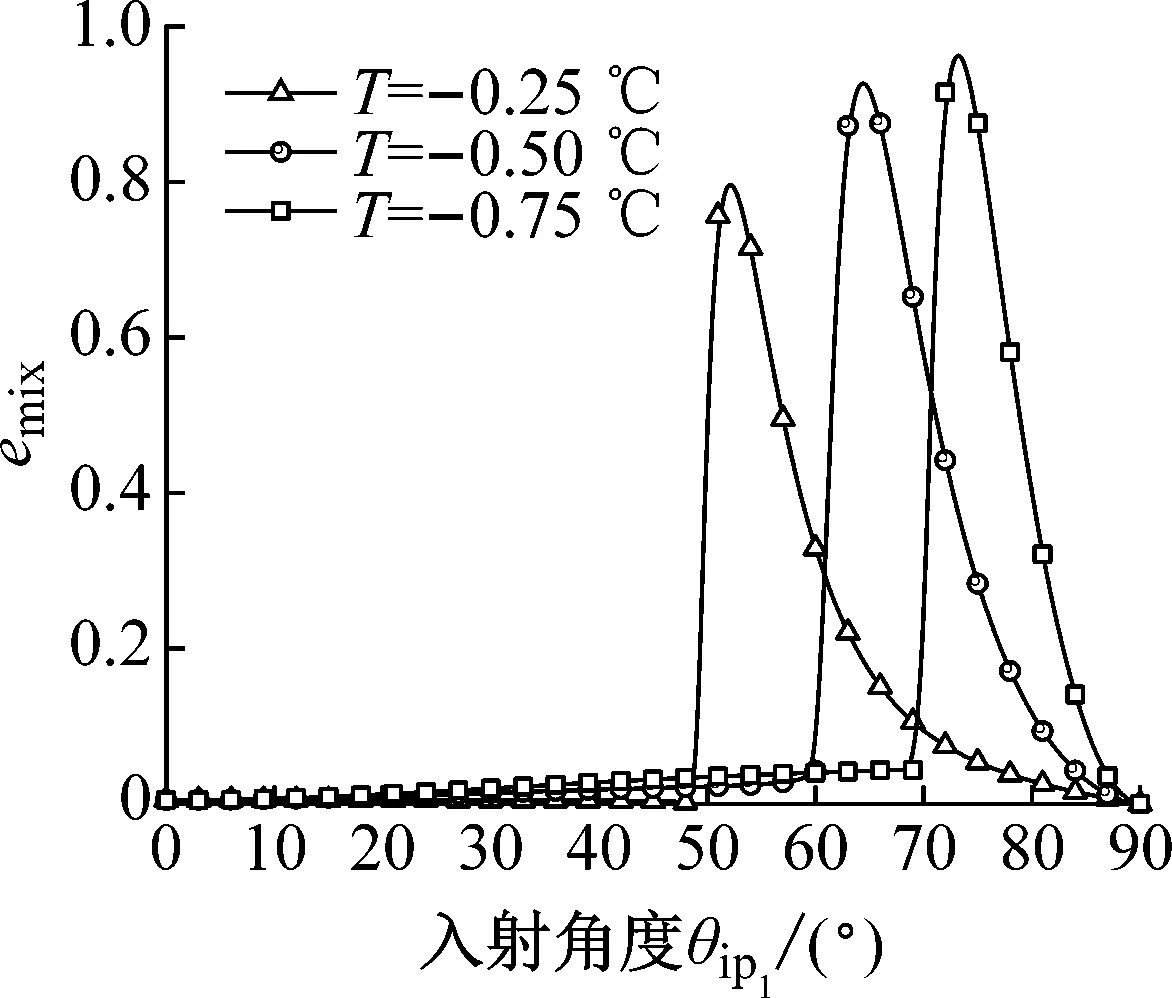
(h) 相互作用波圖4 不同溫度下透反射波能量率隨入射角的變化曲線Fig.4 The energy ratio curve of transmitted and reflected waves with the incident angle under different temperatures
4.4 膠結參數對透反射波能量率的影響
根據Luo等[41]和劉志軍[42]的研究結論,整體骨架膠結程度的參數可取為
(71)
式中:v為飽和凍土介質的固體骨架泊松比;α為膠結參數,其物理意義反映了固體骨架的壓縮性。膠結參數隨著泊松比的增加而增大,但沉積土固結程度隨之減弱,即膠結程度而減弱,此時土的物理性質越松散。當膠結參數越小,即膠結程度越強時往往對應巖石等介質。當膠結參數越大,即膠結程度越弱時對應實際工程中軟土或海底沉積物等。
取入射頻率f= 100 Hz,孔隙率φ= 0.3,接觸參數ε=0.5,溫度T= -0.50 ℃(含冰量nI=0.192),其中選取泊松比v為0.1、0.2和0.4,圖5分析了不同膠結參數對能量反射率,能量透射率和能量相互作用率的影響。從圖5(a)~(h)中可以看出,當泊松比的越大時,臨界角越早出現。泊松比對彈性波的能量反射率,能量透射率和能量相互作用率有顯著的影響,其中透射P波以及反射P3波和emix波的能量透反射率和能量相互作用率均隨著泊松比的增加而明顯減小,而透射S波與反射P1、P2、S1和S2波的能量透反射率均隨泊松比的增加而增大。隨著泊松比的增加,反射P1波脈沖峰值越大。因為隨泊松比的增大使得膠結程度減弱,介質往往越松散,換言之說明隨膠結參數α的減弱透射P波、反射P3波和emix波的能量透反射率和能量相互作用率隨之減小,而透射S波與反射P1、P2、S1和S2波的能量透反射率隨α的減弱而增大。

(a) 透射P波

(b) 透射S波

(c) 反射P1波

(d) 反射P2波

(e) 反射P3波

(f) 反射S1波

(g) 反射S2波

(h) 相互作用波圖5 不同膠結參數下透反射波能量率隨入射角的變化曲線Fig.5 The energy ratio curve of transmitted and reflected waves with the incident angle under different cementation parameters
4.5 孔隙率對透反射波能量率的影響
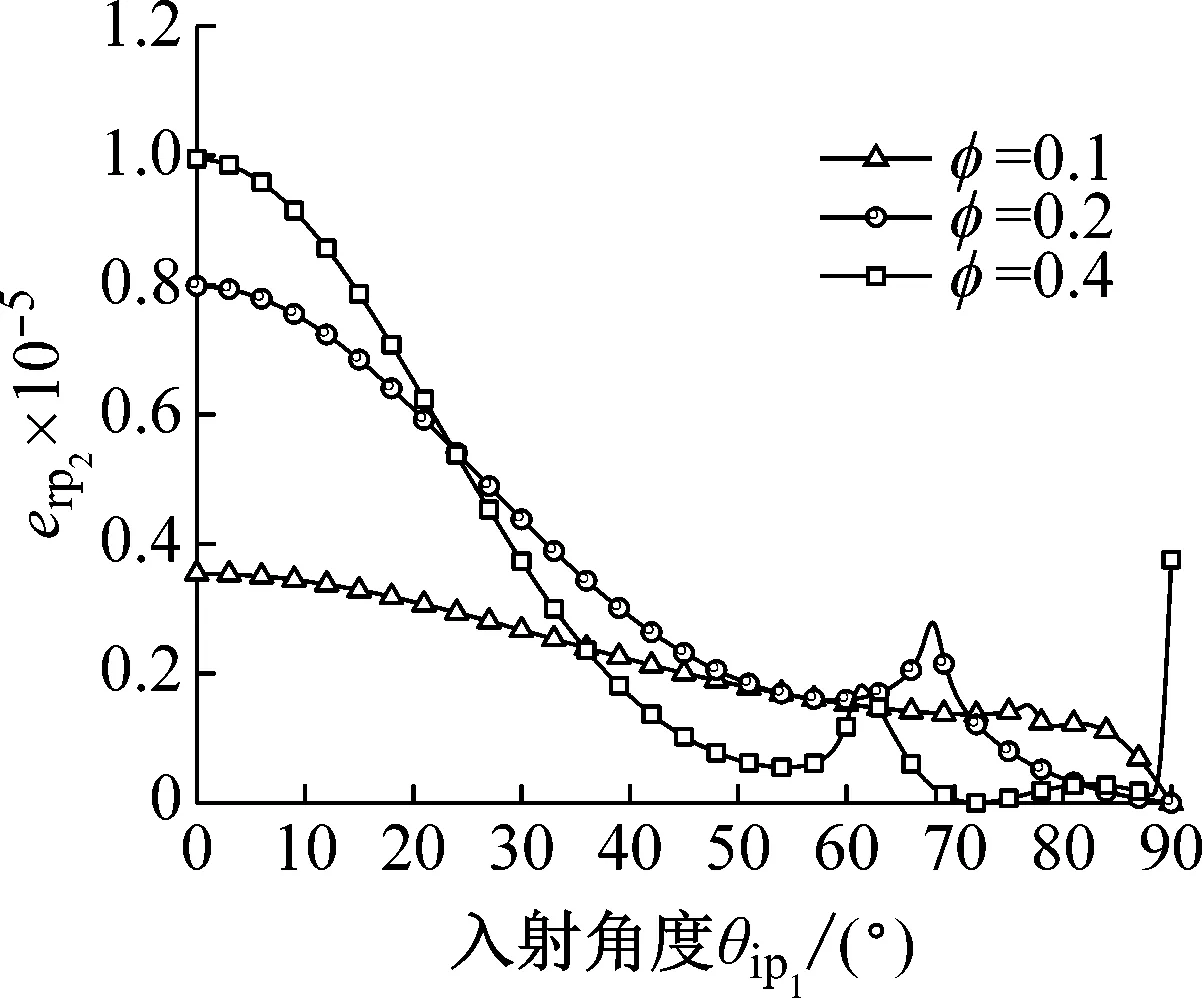
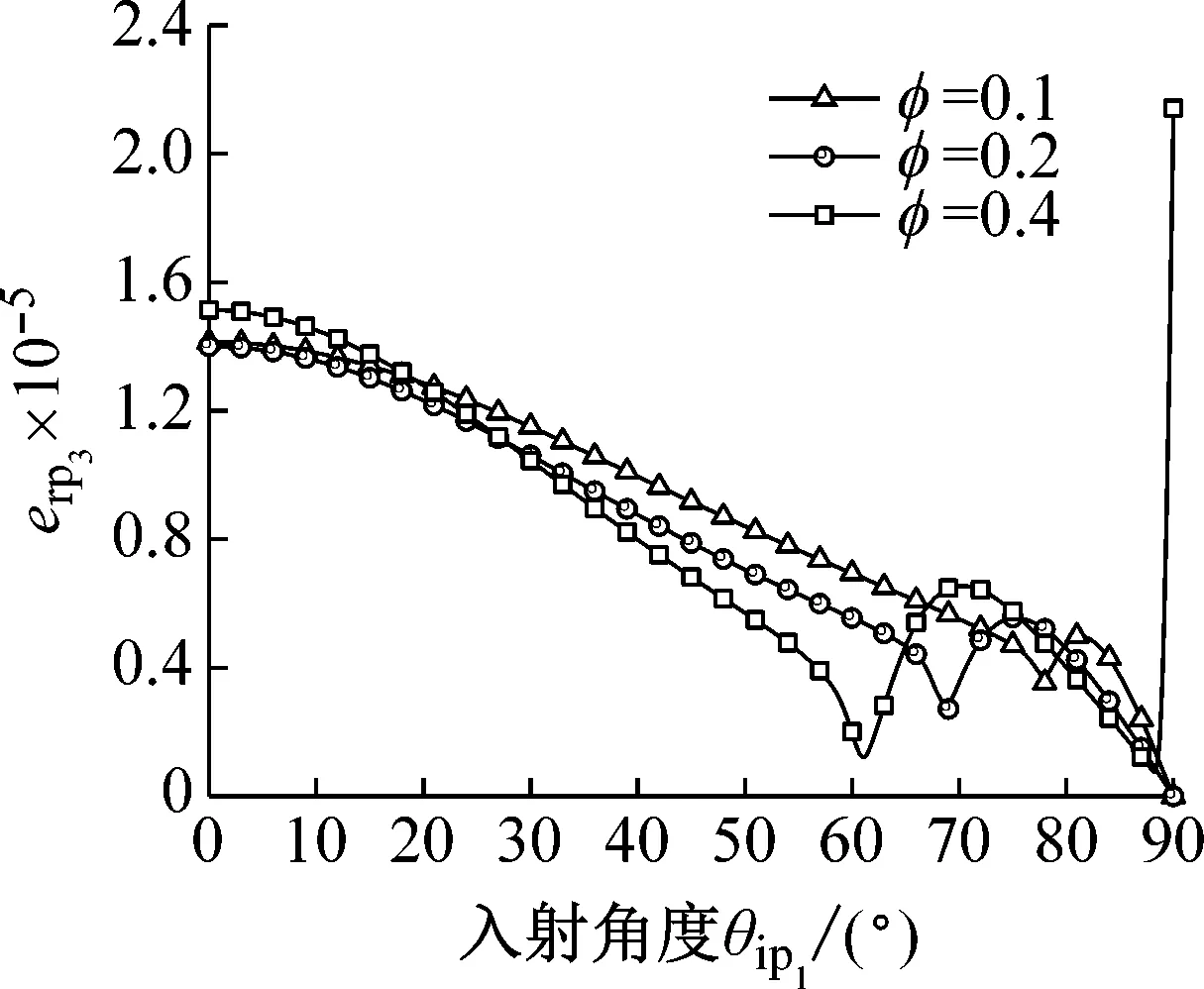
取入射頻率f= 100 Hz,泊松比v= 0.35,接觸參數ε= 0.5,溫度T= -0.50 ℃(含冰量nI=0.192),孔隙率φ取為0.1、0.2、0.4,圖6繪出了不同孔隙率下彈性波的能量反射率、能量透射率和能量相互作用率隨入射角度的變化曲線。從圖6(a)~(h)中可以看出,隨著孔隙率的增加,臨界角越早出現。孔隙率對彈性波的能量透反射率影響顯著,透射P波和反射P3波的能量透反射率均隨孔隙率φ的增加而明顯減小。反之,透射S波以及反射P1、P2、S1、S2波和emix波的能量透反射率和能量相互作用率隨孔隙率的增加而增大。隨著孔隙率的增加,反射P1波的脈沖峰值越大。此外,孔隙率較大的土體密實度較小,但在同樣的凍結溫度下,卻有更多的水凍結成冰,在一定程度上彌補了孔隙率過大造成的影響。因此,在孔隙率較大時透反射波能量率的增長跨度并不明顯。

(a) 透射P波

(b) 透射S波

(c) 反射P1波
(d) 反射P2波
(e) 反射P3波

(f) 反射S1波

(g) 反射S2波

(h) 相互作用波圖6 不同孔隙率下透反射波能量率隨入射角的變化曲線Fig.6 The energy ratio curve of transmitted and reflected waves with the incident angle under different porosity
4.6 接觸參數對透反射波能量率的影響
取入射頻率f= 100 Hz,孔隙率φ= 0.3,泊松比v= 0.35,溫度T= -0.50 ℃(含冰量nI=0.192),在不同接觸參數ε= 0、0.5和1.0時彈性波的能量透反射率和能量相互作用率與入射角度的關系曲線如圖7(a)~(h)所示。已知接觸參數ε在實際條件中反應孔隙中冰顆粒對土骨架的支撐作用,當接觸參數較小時,孔隙冰與土骨架之間摩擦力較大,相對運動幅度較小。當接觸參數越大時,孔隙冰對土骨架的支撐作用減弱,相對運動幅度較大。
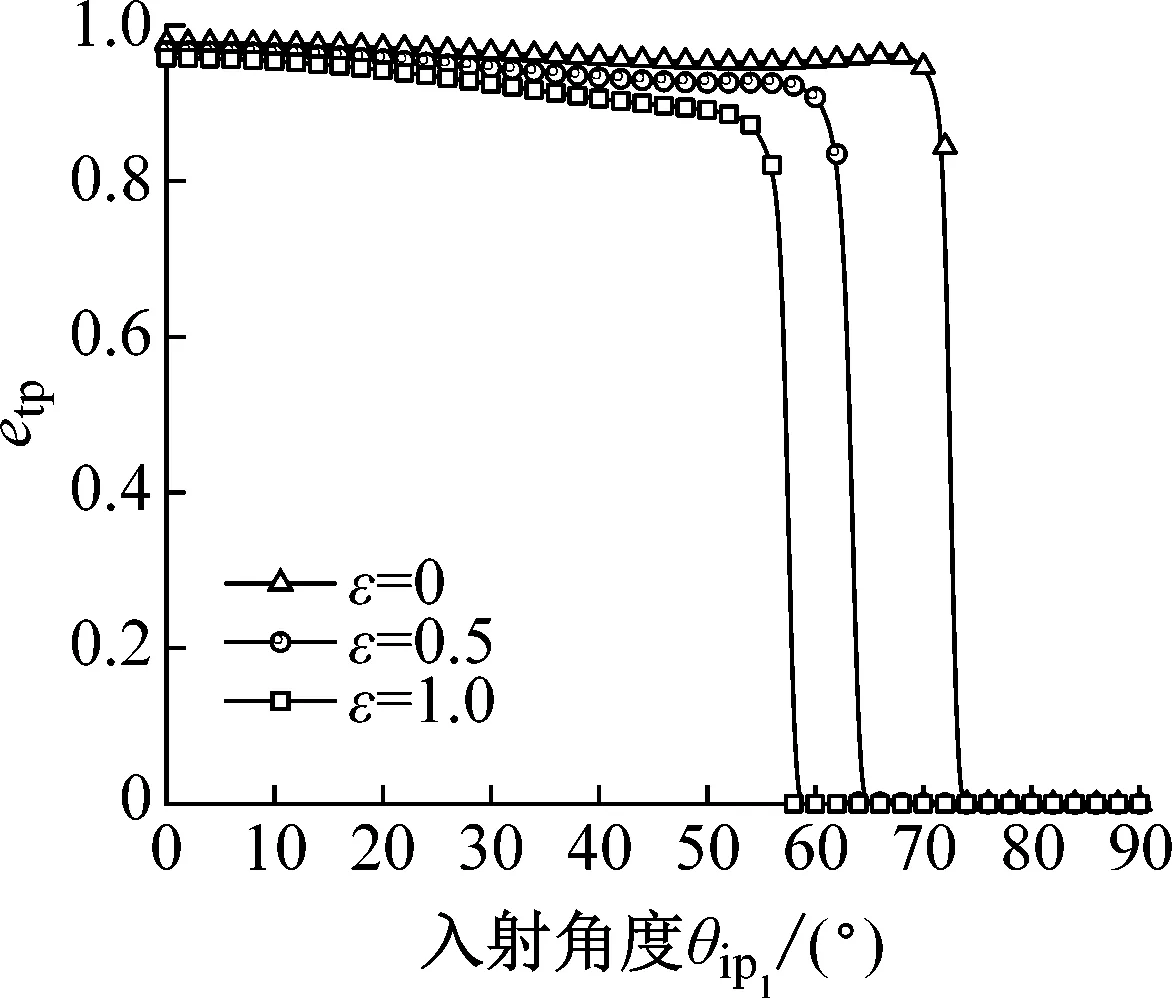
(a) 透射P波

(b) 透射S波

(c) 反射P1波

(d) 反射P2波

(e) 反射P3波

(f) 反射S1波
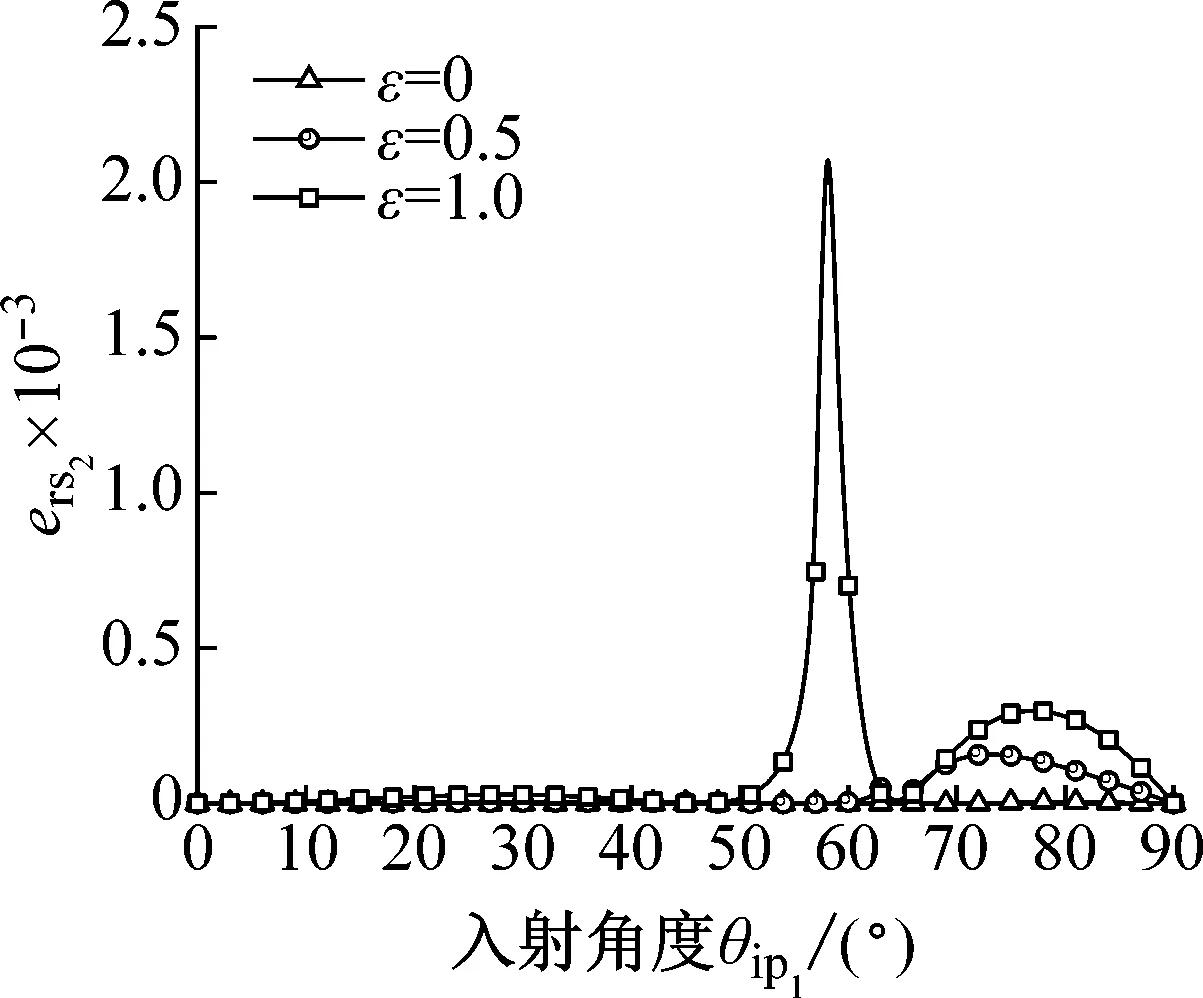
(g) 反射S2波

(h) 相互作用波圖7 不同接觸參數下透反射波能量率隨入射角的變化曲線Fig.7 The energy ratio curve of transmitted and reflected waves with the incident angle under different contact parameters
從圖7(a)~(h)中可以發現,隨著接觸參數的增加,臨界角越早出現。當接觸參數增加時,透射S波、反射P2、S1、S2波和emix波的能量透反射率和能量相互作用率呈現出不同程度的增大,而透射P波和反射P3波能量透反射率隨之降低。接觸參數對反射P1波的影響較小。隨著接觸參數的增加, 反射P1、S2波的脈沖峰值越大。接觸參數對彈性波的能量透反射率有不同程度的影響,其中從數量級的變化對比,透射P波的能量透射率受到影響最大,而從變化幅度來看,其反射P3波的能量反射率受影響最為顯著。
5 結 論
通過波的勢函數以及邊界條件解析推導了反射波與透射波的反射振幅比與透射振幅比,進一步求解出能量透反射率和能量相互作用率。研究了在人工震源處激發出的快壓縮P1波以不同入射角度透過飽和凍土與單相介質分界面上時,入射頻率、溫度(含冰量)、孔隙率、膠結參數和接觸參數對各類波能量率的影響。主要結論總結如下:
(1) 當入射角θip1= 0°時,只有透射P波和3種反射P波產生;當達到臨界角時,反射P1、S1和S2波的反射能量率出現明顯的脈沖,透射P波的能量透射率迅速下降到0,隨后透射P波消失。波在兩種介質分界面上的傳播特性與兩種介質的相對波速相關,當波速越大時(即P1和S1波)占據的傳播能量越大,相反S2波的波速最低占據能量最少。
(2) 入射頻率對反射P2、P3和S2波的能量反射率影響較大,而對透射P、S波與反射P1、S1波和emix波的能量透反射率和能量相互作用率影響較小。當泊松比越大,膠結程度越弱時,透射P波以及反射P3波和emix波的能量透反射率和能量相互作用率越小,而透射S波與反射P1、P2、S1和S2波的能量透反射率越大。溫度對透反射波的能量率影響較大,即冰顆粒的含量對飽和凍土介質和彈性基巖波的透反射特性影響顯著。隨著泊松比、孔隙率和接觸參數的增加,臨界角越早出現。
(3) 出現臨界角時或溫度較高時對反射波和透射波有負面影響,即分界面上能量耗散越大。在未出現臨界角時能量相互作用率在數量級上表現很小,且各類參數對其影響較小。但在臨界角附近時,能量相互作用率出現顯著的脈沖峰值,數值上比未出現臨界角時大好幾個數量級。因此在分析飽和凍土與彈性基巖分界面上的能量輸出特性時,能量相互作用率應被考慮。
附錄A
式(5)~(10)、(14)~(16)和(28)~(29)中系數的表達式為
c23=ρ23ω2-b23iω,c23=c32,ρ11=a13nSρS+(a12-1)nFρF+(a31-1)nIρI,

ρ33=(a13-1)nSρS+(a23-1)nFρF+a31nIρI,ρ12=-(a12-1)nFρF,
ρ23=-(a23-1)nFρF,ρ13=-(a13-1)nSρS-(a31-1)nIρI,
R33=[(1-c3)nI]2Kav+Kim+4μ33/3,R12=(1-c1)nSnFKav,
R23=(1-c3)nInFKav,R13=(1-c1)(1-c3)nSnIKav+2μ13/3,
K1=((1-c1)nS)2Kav+Ksm,C12=(1-c1)nSnFKav,
K3=[(1-c3)nI]2Kav+Kim,C23=(1-c3)nInFKav,
C13=(1-c1)(1-c3)nSnIKav,μ13=(1-g1)(1-g3)μav,
μ11=[(1-g1)nS]2μav+μsm,c1=Ksm/(nSKS),
μ33=[(1-g3)nI]2μav+μim,c3=Kim/(nIKI),g1=μsm/(nSμS),
g3=μim/(nIμI),Kim=nIKI/[1+α(1-nI)],
Ksm=(1-nF-εnI)KS/[1+α(nF+εnI)],
μsm=(1-nF-εnI)μS/[1+αγ(nF+εnI)]。
式中:aij為j相對i相的扭曲度(彎曲度);rij為孔隙微觀特征,對于球形顆粒rij=0.5;κS和κI分別為飽和凍土骨架和冰骨架動力滲透系數;κS0和κI0分別為飽和凍土骨架和冰骨架動力滲透系數參考值和流體動力黏滯系數ηF;Ksm、Kim和μsm、μim分別為土骨架和冰骨架的體變模量和剪切模量;Kav和μav為三相介質的不排水的體變模量和剪切模量;c1、c3和g1、g3分別為土骨架和冰骨架固結系數;KS、KF和KI分別為三相的體變模量;μS和μI分別為土顆粒和冰顆粒的剪切模量;ε為接觸參數;δFPβ表示為各種壓縮波相關的孔隙流體的振幅值與土骨架振幅值的比值;δIPβ表示為各種壓縮波相關的冰顆粒的振幅值與土骨架振幅值的比值;δFSα表示為各種剪切波相關的孔隙流體的振幅值與土骨架振幅值的比值;δISα表示為各種剪切波相關的冰顆粒的振幅值與土骨架振幅值的比值。
附錄B
矩陣(53)中m11~m77的系數如下


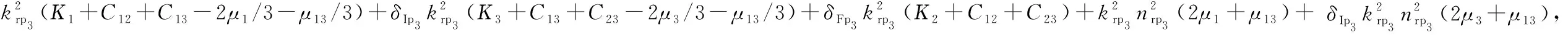



m31=-ktpltp,m32=ktsnts,m33=krp1lrp1,m34=krp2lrp2,m35=krp3lrp3,
m36=krs1nrs1,m37=krs2nrs2,m41=0,m42=0,
m43=krp1lrp1(1-δIp1),m44=krp2lrp2(1-δIp2),m45=krp3lrp3(1-δIp3),
m46=krs1nrs1(1-δIs1),m47=krs2nrs2(1-δIs2),m51=ktpntp,
m52=ktslts,m53=krp1nrp1,m54=krp2nrp2,m55=krp3nrp3,
m56=-krs1lrs1,m57=-krs2lrs2,m61=0,m62=0,
m63=krp1nrp1(1-δFp1),m64=krp2nrp2(1-δFp2),
m65=krp3nrp3(1-δFp3),m66=krs1lrs1(δFs1-1),m67=krs2lrs2(δFs2-1),
m71=0,m72=0,m73=krp1nrp1(1-δIp1),m74=krp2nrp2(1-δIp2),
m75=krp3nrp3(1-δIp3),m76=krs1lrs1(δIs1-1),m77=krs2lrs2(δIs2-1)。
矩陣(53)中q1~q7的系數如下:

q4=kip1lip1(δIp1-1),q5=kip1nip1,q6=kip1nip1(1-δFp1),
q7=kip1nip1(1-δIp1)。
附錄C

