功能梯度石墨烯增強多孔復合材料階梯圓柱殼的振動特性

徐宏達, 王 宇, 徐自強, 賈小羽, 于曉光

(遼寧科技大學 機械工程與自動化學院,遼寧 鞍山 114051)

功能梯度石墨烯增強復合材料因具有極高的楊氏模量、拉伸強度以及優異的導熱性能,被廣泛應用于航天航空、土木工程、兵器和核能等領域[1-2]。將石墨烯片填充到泡沫金屬中,形成了功能梯度石墨烯增強多孔復合材料(functionally graded graphene platelet reinforced porous composite, FG-GPLRPC),兼具多孔材料的輕質性和石墨烯片的優異力學性能,還具有一定的減振性能[3],因此受到廣大學者的關注。圓柱殼常常用于導彈外殼和航空發動機機匣等關鍵結構[4],但復雜工況下有時變厚度階梯圓柱殼更適用于工程應用,例如運載火箭。為了提高圓柱殼的力學性能,同時減輕結構的重量,考慮到FG-GPLRPC力學性能的潛力,因此將FG-GPLRPC應用到階梯圓柱殼結構中具有重要的科學意義。

對于復合材料板殼結構,許多學者進行了動力學研究,例如:Wang[5]、Li等[6-7]和Shen等[8]。對于功能梯度石墨烯增強復合材料圓柱殼,Feng等[9]首先將功能梯度材料引入到功能梯度石墨烯增強復合材料。Liu等[10]采用基于三維彈性理論的狀態空間公式,研究了非均勻分布石墨烯增強復合材料的初始應力功能梯度圓柱殼的屈曲和自由振動。Baghbadorani等[11]基于殼體的一階剪切變形理論和Donnell運動學關系,研究了石墨烯增強復合材料圓柱殼的自由振動。Qin等[12]根據Donnell殼理論和人工彈簧技術,研究了石墨烯增強復合材料圓柱殼在靜止和旋轉狀態下的自由振動,并評估了邊界彈簧剛度、石墨烯的質量分數、總層數和幾何參數對殼體振動特性的影響。對于FG-GPLRPC相關的構件,主要圍繞在均勻無厚度變化的結構進行研究,以下成果為本文研究提供了有價值的參考:Kitipornchai等[13]率先將FG-GPLRPC作為研究對象,討論了FG-GPLRPC梁的自由振動和彈性屈曲行為。基于Timoshenko梁理論,Chen等[14]研究了石墨烯增強泡沫金屬多層功能梯度多孔納米復合材料梁的非線性自由振動和后屈曲行為。Wang等[15]采用改進的Donnell非線性殼理論對FG-GPLRPC圓柱殼進行了非線性振動分析。Yang等[16]通過使用一階剪切變形理論來考慮橫向剪切應變和切比雪夫-里茲法研究了FG-GPLRPC板的屈曲和自由振動行為,并對石墨烯的質量分數、幾何參數以及孔隙系數的影響進行了全面的參數研究。Dong等[17]分別采用一階剪切變形理論和Donnell殼體理論,研究了FG-GPLRPC旋轉圓柱殼的線性和非線性自由振動。Wang等[18]考慮了不同類型的孔隙率和石墨烯分布模式,對石墨烯增強金屬泡沫圓柱殼進行了非線性振動分析。Li等[19]討論了在黏彈性阻尼邊界條件下FG-GPLRPC涂層對纖維增強復合材料板的減振效果。

對于階梯圓柱殼結構的動力學特性分析,李海超等[20-21]用懲罰參數法和Jacobi-Ritz法對具有任意邊界條件的階梯圓柱殼自由振動進行了分析,并驗證了方法的合理性。Zhang等[22]基于Flüggle薄殼理論,對變厚度的階梯圓柱殼和開口階梯圓柱殼振動特性進行了研究。杜夷斐等[23]研究了在軸向沖擊載荷作用下階梯圓柱殼的屈曲行為。Chen等[24]分析了不連續厚度圓柱殼的自由振動和強迫振動。Li等[25]提出了用特征正交多項式處理功能梯度多孔階梯圓柱殼熱振動特性的一般方法。

綜上所述,目前復合材料圓柱殼結構振動特性的研究較多,關于階梯圓柱殼的動力學研究主要集中在單一材料,而對于復合材料階梯圓柱殼的研究較少,尤其是彈性邊界條件下的FG-GPLRPC階梯圓柱殼,因此開展此殼體結構的振動特性研究具有重要意義和應用前景。本文基于一階剪切變形理論,利用人工彈簧技術模擬任意邊界條件,采用Jacobi-Ritz法求解其階梯圓柱殼的振動頻率,驗證所提出方法的有效性,討論各參數對殼體結構振動特性的影響。

1 理論方法

1.1 FG-GPLRPC階梯圓柱殼力學模型

如圖1(a)建立FG-GPLRPC階梯圓柱殼的力學模型,在殼體中面定義柱坐標系(x,θ,z),O為坐標原點,軸向x、切向θ和徑向z三個方向的位移分量分別由u、v和w表示,殼體中面半徑為R,殼體總長度為L,如圖1(b)所示,每個殼段長度為L1、L2…、Lp,每個殼段厚度為h1、h2…、hp。為了便于文中數學計算和表達,定義無量綱坐標η=x/L,因此?/?x=(1/L)?/?η。

(a) FG-GPLRPC階梯圓柱殼模型

(b) FG-GPLRPC階梯圓柱殼截面圖

(c) 邊界約束彈簧圖1 FG-GPLRPC階梯圓柱殼模型及邊界約束彈簧Fig.1 FG-GPLRPC stepped cylindrical shell model and boundary constrained spring

1.2 FG-GPLRPC階梯圓柱殼的材料屬性

對于功能梯度石墨烯增強復合材料階梯圓柱殼,沿厚度方向對不同含量的石墨烯片進行分層,考慮階梯圓柱殼五種石墨烯分布模式如圖2所示。顏色深淺代表石墨烯的含量,顏色深的代表石墨烯含量多,反之石墨烯含量少。GPL-UD呈均勻分布,其余四種呈梯度分布,其中GPL-X表現為殼體外側和內側石墨烯含量多的分布模式,GPL-O表現為中面石墨烯含量多并向兩側逐漸減少,GPL-V表現為外側石墨烯含量多并向內側逐漸減少,GPL-A表現為內側石墨烯含量多并向外側逐漸減少。通過考慮五種石墨烯分布模式,得到對應殼體第k層石墨烯的體積分數為

(a) GPL-UD

(b) GPL-X

(c) GPL-O

(d) GPL-V

(e) GPL-A圖2 石墨烯分布模式示意圖Fig.2 Schematic diagram of graphene distribution patterns

石墨烯的總體積分數由石墨烯的密度和質量分數以及基體密度決定,由式(2)表示

(2)

式中:WGPL為石墨烯的質量分數;ρGPL為石墨烯的密度;ρm為基體的密度。

基于Halpin-Tsai微觀力學模型[26],功能梯度石墨烯增強復合材料的彈性模量為

(3)

式中:Em表示基體材料的彈性模量;ηL和ηW表示與石墨烯以及基體材料彈性模量相關的參數;ξL和ξW表示與石墨烯長度LGPL、寬度wGPL和厚度hGPL相關的參數。分別表示為

(4)

功能梯度石墨烯增強復合材料階梯圓柱殼第k層的有效密度、泊松比和剪切模量表示為

(5a)

(5b)

(5c)

式中:μGPL為石墨烯的泊松比;μm為基體的泊松比。

如果將基體材料替換成多孔材料,就將形成FG-GPLRPC,兼具多孔材料的輕質性和石墨烯片的優異力學性能,同時這種復合材料具有更好的工程應用前景,因此,開展對其復合材料振動特性研究首先就要了解其復合材料的有效材料屬性。沿厚度方向考慮三種孔隙分布類型,如圖3所示。

(a) 類型Ⅰ

(b) 類型Ⅱ

(c) 類型Ⅲ圖3 孔隙分布類型示意圖Fig.3 Schematic diagram of porosity distribution types

用孔隙系數e0來表示孔隙的分布情況,FG-GPLRPC三種孔隙分布類型的彈性模量、剪切模量和密度依次表示為

類型Ⅰ:

(6a)

(6b)

(6c)

類型Ⅱ:

(7a)

(7b)

(7c)

類型Ⅲ:

E(z)(k)=E(k)α

(8a)

G(z)(k)=G(k)α

(8b)

ρ(z)(k)=ρ(k)α′

(8c)

根據開胞體理論[27],由式(9)表示

(9)

通過式(9)可以建立不同孔隙分布類型的密度系數和孔隙系數之間的關系,表示為

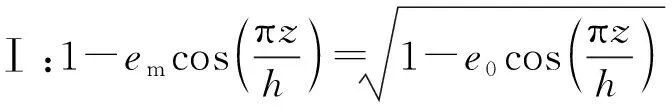
類型Ⅱ:

(10)

通過設置具有不同孔隙系數和石墨烯分布的殼體質量相等,得出如式(11)表示

(11)

由式(10)可見,已知類型Ⅰ的孔隙系數e0,可求出三種孔隙分布類型的密度系數,再通過式(11)可求出另外兩種孔隙分布類型的孔隙系數。

2 FG-GPLRPC階梯圓柱殼振動控制方程

基于一階剪切變形理論,圓柱殼上任意一點沿著x、y和z軸方向的位移表示如下

u(η,θ,z,t)=u0(η,θ,t)+zφx(η,θ,t)

(12a)

v(η,θ,z,t)=v0(η,θ,t)+zφθ(η,θ,t)

(12b)

w(η,θ,z,t)=w0(η,θ,t)

(12c)

式中:u0、v0和w0為殼體中面位移;φx和φθ分別為殼體任意點處橫截面繞θ軸和x軸的轉角。

應變分量表示為

(13)

(14a)

(14b)

(14c)

κxz(i)=0,κθz(i)=0

(14d)

利用廣義胡克定律可以得到以下關系

(15)

(16)

沿x和θ方向中面上的內力、內力矩和橫向剪切力由式(17)表示

(17a)

(17b)

(17c)

式中:κ為修正系數,取值5/6;hk和hk+1表示厚度方向每一層的位置坐標。

沿x和θ方向中面上的內力、力矩和橫向剪切力與曲率的關系如下

(18)

式中,Aij、Bij和Dij(i,j=1,2,6)分別是拉伸剛度、耦合剛度和彎曲剛度。表示為

(19)

FG-GPLRPC階梯圓柱殼的第i殼段動能T(i)為

(20)

式中,慣性項I0,I1,I2分別表示為

(21)

第i殼段應變能Uε(i)表示為

(22)

邊界彈簧所儲存的彈性勢能Ub為

(23)

相鄰殼段之間的附加勢能Us(i)表示為

(24)

采用統一的Jacobi多項式作為容許函數,將FG-GPLRPC階梯圓柱殼的位移場展開為

(25a)

(25b)

(25c)

(25d)

(25e)

式中:Am,Bm,Cm,Dm,Em為未知系數;m和n分別為軸向半波數和周向波數;ω為固有角頻率;M為最大截斷數;Pm為Jacobi多項式。在區間[-1,1]之間的遞推關系如式(26)[28](α>-1,β>-1),因為η∈[0,1],使其t區間控制在[-1,1],因此令t=2η-1。定義α=0,β=0。

(26a)

(26b)

(26c)

取各能量表達式的最大值,采用Jacobi-Ritz法得到拉格朗日能量方程表示為

(27)

式中,Np表示殼段數。

對式(27)未知系數q求導,由式(28)表示

(28)

其中,

(29)

通過式(28)得到FG-GPLRPC階梯圓柱殼振動控制方程為

(Kε+Kb+Ks-ω2M)qT=0

(30)

式中:Kε、Kb、Ks和M分別表示為勢能矩陣、邊界剛度矩陣、連接剛度矩陣和質量矩陣。

3 模型收斂性和有效性驗證

3.1 模型參數

表1 圓柱殼的材料屬性Tab.1 Material properties of cylindrical shell

3.2 收斂性和有效性驗證

本文采用懲罰參數法分析FG-GPLRPC階梯圓柱殼,可以更改任意殼段的厚度和長度,需要考慮殼段數對收斂性的影響,在GPL-UD分布模式、孔隙系數e0=0.2下,三種孔隙分布類型不同殼段數對FG-GPLRPC均勻圓柱殼無量綱頻率的影響如表2所示。可以看出,殼段數在NP=2就具有很好的收斂性,因此下文研究取殼段數NP=2,以兩階梯圓柱殼作為研究對象。

表2 殼段數對FG-GPLRPC均勻圓柱殼無量綱頻率影響Tab.2 Influence of shell segment number on dimensionless frequency of FG-GPLRPC uniform cylindrical shell

采用Jacobi-Ritz法求解殼體頻率時,為了提高計算效率,需要對振型函數展開項截斷數進行分析,FG-GPLRPC階梯圓柱殼對殼體無量綱頻率收斂性的分析如表3所示。由表3可知,當截斷數M=6時,頻率計算結果已經達到收斂,說明Jacobi多項式具有很好的收斂性。文中截斷數均取M=6。

表3 截斷數對FG-GPLRPC階梯圓柱殼無量綱頻率的影響Tab.3 Influence of truncation number on dimensionless frequency of FG-GPLRC stepped cylindrical shell

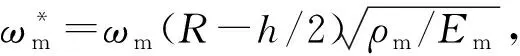
表4 功能梯度石墨烯增強復合材料圓柱殼無量綱頻率對比Tab.4 Dimensionless frequency comparison of functionally graded graphene platelet reinforced porous composite cylindrical shell

(31)

對于以泡沫金屬銅為基體組成的FG-GPLRPC圓柱殼,簡支-簡支邊界條件下,其中將石墨烯分布模式定為GPL-UD,通過文獻[3]進行驗證如表5所示。可以發現,分析結果與文獻[3]結果最大誤差為0.23%,具有較好的一致性,適于分析FG-GPLRPC圓柱殼。

表5 FG-GPLRPC圓柱殼無量綱頻率對比Tab.5 Dimensionless frequency comparison of FG-GPLRPC cylindrical shell

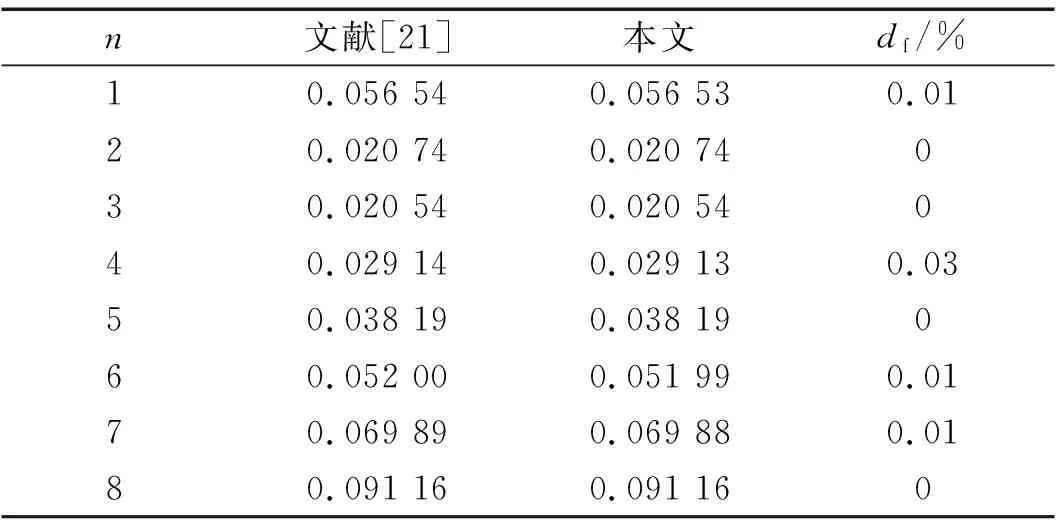
表6 階梯圓柱殼無量綱頻率對比Tab.6 Dimensionless frequency comparison of stepped cylindrical shell

4 數值分析和討論

4.1 層數的影響

在GPL-UD分布模式下,不同孔隙類型層數對FG-GPLRPC階梯圓柱殼無量綱頻率的影響如表7所示。結果表明,不同孔隙分布類型下殼體結構的頻率不會隨殼體層數的增加或減少而變化,說明層數對頻率影響較小,下文選取層數為NL=10進行研究。

表7 層數對FG-GPLRPC階梯圓柱殼無量綱頻率影響Tab.7 Influence of layer numbers on dimensionless frequency of FG-GPLRPC stepped cylindrical shell

4.2 孔隙系數的影響

在分別給定同一石墨烯分布類型和孔隙類型前提下,各孔隙分布類型以及石墨烯分布模式的無量綱頻率隨孔隙系數的變化如圖4所示。由圖4可知,FG-GPLRPC階梯圓柱殼頻率隨著孔隙系數的增大而減小,這是由于較高的孔隙系數表示殼體中有較密集和較大的孔隙,削弱了圓柱殼結構的剛度。圖4(a)中可以看出,五種石墨烯分布模式中,GPL-X分布模式下殼體頻率最高,具有最佳的剛度增強效果;圖4(b)中可以發現,四種孔隙分布類型中,孔隙分布類型Ⅱ的殼體結構具有最大的結構剛度。為了分析方便,下文選取GPL-UD分布模式和孔隙分布類型Ⅰ進行研究。

(a) 類型Ⅰ

(b) GPL-UD分布模式圖4 孔隙系數對FG-GPLRPC階梯圓柱殼無量綱頻率影響Fig.4 Influence of porosity coefficient on dimensionless frequency of FG-GPLRPC stepped cylindrical shell

4.3 石墨烯質量分數的影響

石墨烯質量分數對FG-GPLRPC階梯圓柱殼無量綱頻率的影響如圖5所示。可以發現,頻率隨著石墨烯質量分數的增大而增大,當石墨烯質量分數為零時,殼體的頻率最小,質量分數為1%時頻率最大,說明石墨烯對殼體結構的剛度具有明顯的增強效果。這是因為石墨烯質量分數的增大導致FG-GPLRPC彈性模量的增大,從而增加了殼體結構的固有頻率和剛度。如果沒有額外說明,下文選取質量分數1%進行研究。

(a) m=1,n=1

(b) m=1,n=2圖5 石墨烯質量分數對FG-GPLRPC階梯圓柱殼無量綱頻率的影響Fig.5 Influence of graphene platelet mass fraction on dimensionless frequency of FG-GPLRPC stepped cylindrical shell

4.4 尺寸參數的影響

圓柱殼長徑比和徑厚比對FG-GPLRPC階梯圓柱殼無量綱頻率的影響如圖6所示。結果表明,當圓柱殼徑厚比一定時,隨著圓柱殼長徑比的增大,殼體頻率減小;當長徑比一定時,無論徑厚比如何變化,頻率的變化都較小。因此可以看出,長徑比較大的圓柱殼對應較低的頻率,較薄和較長的圓柱殼表現出較小的剛度,而徑厚比對階梯圓柱殼的振動特性影響較小。

(a) 圓柱殼長徑比

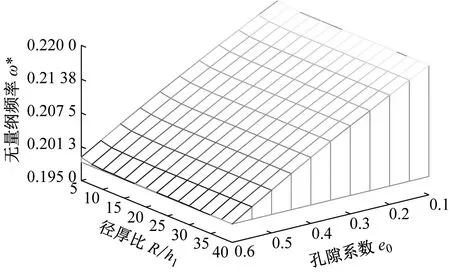
(b) 圓柱殼徑厚比圖6 圓柱殼的尺寸參數對FG-GPLRPC階梯圓柱殼無量綱頻率的影響Fig.6 Influence of dimension parameters of cylindrical shells on dimensionless frequency of FG-GPLRPC stepped cylindrical shell

石墨烯片長寬比和長厚比對FG-GPLRPC階梯圓柱殼無量綱頻率的影響如圖7所示。當長厚比給定時,頻率隨著石墨烯片長寬比的增大而減小;同時不同長寬比殼體之間頻率相差在0.01之間,說明石墨烯片的長寬比對頻率的影響較小。當長寬比給定時,隨著石墨烯片長厚比的增大,殼體頻率增大;此外,當石墨烯片的長厚比超過102時對頻率的影響逐漸變小。

(a) 石墨烯片長寬比

(b) 石墨烯片長厚比圖7 石墨烯片的尺寸參數對FG-GPLRPC階梯圓柱殼無量綱頻率的影響Fig.7 Influence of size parameters of graphene platelet on dimensionless frequency of FG-GPLRPC stepped cylindrical shell

4.5 邊界彈簧剛度值的影響

為了研究邊界彈簧剛度值的影響,設置平動和旋轉彈簧剛度值從102增加到1014,當平移或旋轉彈簧剛度值增加時,另一組彈簧的剛度保持不變,計算各個剛度值的FG-GPLRPC階梯圓柱殼無量綱頻率如圖8所示。由圖8可知,頻率變化有三個階段,在開始階段,頻率保持不變且頻率較低;第二階段頻率明顯增加;最后頻率再次保持穩定不變。此外還可以發現,平動彈簧剛度值頻率的變化幅度高于旋轉彈簧,頻率突然增加時的剛度值小于旋轉彈簧。

(a) 平動彈簧剛度

(b) 旋轉彈簧剛度圖8 邊界彈簧剛度值對FG-GPLRPC階梯圓柱殼無量綱頻率的影響Fig.8 Influence of boundary spring stiffness values on the dimensionless frequency of FG-GPLRPC stepped cylindrical shell

4.6 無量綱頻率隨周向波數的變化規律

不同孔隙分布類型下FG-GPLRPC均勻圓柱殼和階梯圓柱殼隨周向波數的變化如圖9所示。可以看出,三種孔隙分布類型都隨著周向波數的增大呈現先減小后增大的趨勢,表明m=1,n=1不是所有模態振型中頻率最小的;在孔隙分布類型Ⅰ下,周向波數對頻率的影響比在類型Ⅱ和Ⅲ時顯著;當周向波數n>3時,階梯圓柱殼比均勻圓柱殼頻率低,且變化程度相較于均勻圓柱殼小;當所有孔隙類型波數小時頻率接近,波數大時差別越來越明顯,因此孔隙類型在較高模態對殼體振動特性的影響更加顯著。

圖9 無量綱頻率隨周向波數的變化Fig.9 Variation of dimensionless frequency with circumferential wave numbers

5 結 論

本文以FG-GPLRPC階梯圓柱殼為研究對象,基于一階剪切變形理論、懲罰參數法和Jacobi-Ritz法,研究了FG-GPLRPC階梯圓柱殼的振動特性。主要結論如下:

(1) 驗證了本文方法的有效性和收斂性,當殼段數為2且截斷數為6時具有良好的收斂性和計算效率,適用于FG-GPLRPC階梯圓柱殼的振動特性分析。

(2) 層數對FG-GPLRPC階梯圓柱殼頻率影響較小;孔隙系數對頻率的影響較大,表現為孔隙系數增大時頻率減小;石墨烯含量對階梯圓柱殼具有明顯的剛度增強效果,表現為石墨烯質量分數增大,頻率增大;同時,GPL-X分布模式和孔隙分布類型Ⅱ具有最佳的增強效果。

(3) 尺寸參數對頻率的影響不同,具體表現為階梯圓柱殼長徑比增大時頻率明顯減小,而徑厚比的變化對頻率的影響較小;石墨烯片長寬比增大時頻率減小,而長厚比增大時頻率呈增大趨勢。

(4) 平動彈簧對殼體頻率的影響大于旋轉彈簧,表現為平動彈簧剛度值頻率的變化幅度高于旋轉彈簧,頻率突然增加時的剛度值小于旋轉彈簧。FG-GPLRPC階梯圓柱殼的頻率隨著周向波數的增大呈現出先減小后增大的趨勢;在三種孔隙分布類型下,類型Ⅰ的變化程度最大。