基于微分法的大跨度橋梁三維顫振敏感性分析

翁祥穎, 董 銳, 葛耀君

(1. 福建理工大學 福建省土木工程新技術與信息化重點實驗室, 福州 350118;2. 福州大學 土木工程學院, 福州 350118; 3. 同濟大學 土木工程防災減災國家重點實驗室, 上海 200092)

橋梁顫振是一種災難性的橋梁風致失穩破壞形式,在設計階段提升大跨度橋梁的顫振性能對橋梁結構的安全性和經濟性具有重要意義。為此,研究人員開展了大量的研究工作,不斷探究橋梁結構動力特性和氣動外形等設計參數對橋梁顫振性能的影響規律,以期深入了解橋梁顫振機理,為工程實踐提供更加有效的指導和支撐。

在大跨度橋梁設計階段,設計人員需要快速準確地預測橋梁顫振性能對設計變量的響應,從而提出具有理想顫振性能的設計方案。上述各種方法揭示了各類設計參數對橋梁顫振性能的影響規律,但對于設計人員而言,這些方法的實現或應用門檻相對較高,在初步設計階段的橋梁氣動選型時,仍需要花費較大的時間和人力成本。

敏感性指標反映了設計參數變化對系統輸出的影響程度,廣泛應用于航空、車輛、造船等工業設計過程。敏感性分析常采用有限差分法、直接微分法等手段,其原理簡單,計算速度快,尤其適用于設計階段幫助設計人員快速掌握相關參數變化對橋梁結構顫振性能的影響規律。目前常用的橋梁顫振敏感性分析方法主要是依托于參數化分析的有限差分法,其原理簡單,但是隨著設計變量增多,該方法將面臨計算成本和時間成本問題。此外,有限差分法對數值噪聲敏感,要求數值計算精度較高,無疑進一步增加了相關成本。與有限差分法相比,直接微分法計算效率高、計算結果準確,且通用性更強。受限于橋梁顫振相關變量之間復雜的依賴關系,尤其是顫振導數對風速的隱式依賴關系,采用直接微分法研究橋梁顫振敏感性的相關報道較少。

本文從特征值問題敏感性出發,利用橋梁顫振狀態矩陣的左右特征向量正交特性,構建了在設計參數小幅攝動時橋梁多模態耦合顫振規格化條件,結合橋梁顫振臨界條件,得到了橋梁三維耦合顫振系統的特征值及顫振臨界風速對設計參數的敏感性表達式。通過對比有限差分法和參數化計算得到的理想平板斷面簡支梁橋顫振敏感性,檢驗本文方法的準確性和高效性。針對一座主跨918 m的懸索橋,運用本文方法研究結構參數和氣動參數對橋梁顫振性能的影響規律。本文的研究工作有助于精確且高效地量化相關設計參數對橋梁顫振性能的影響規律,為設計階段橋梁高效地開展氣動選型提供技術支撐。

1 橋梁三維顫振局部敏感性分析方法

以Scanlan[10]自激力模型表述的橋梁三維顫振運動方程為

(1)

式中:M、C和K分別為橋梁結構的模態質量、阻尼和剛度矩陣;列向量q為模態參與向量;ρ為空氣密度;B為橋面寬度;U為來流風速;As和Ad分別為廣義氣動剛度和氣動阻尼矩陣。

(2)

(3)

(4)

(5)

式是:K=Bω/U為折算頻率;Φ為橋梁模態振型矩陣;diag(*)表示以*為元素的對角矩陣;上標T表示轉置運算。

1.1 有限差分法

有限差分法是最簡單的敏感性分析方法,通過假定被研究的參數發生小幅擾動,利用差分計算近似得到參數的敏感性。前向差分和中心差分是兩種最常用的差分格式,以前向差分為例,其計算過程如下

(6)

式中:r為目標函數;t、θ為變量;Δθ為相對于θ0的小幅擾動。有限差分法用于敏感性分析時具有簡單、靈活及通用性強的優點。

以參數化計算為基礎,有限差分法常用于研究橋梁結構的動力特性、氣動外形、氣動導數等參數對橋梁顫振臨界風速的影響規律[11-14]。由于有限差分結果對噪聲及誤差敏感,因此這類研究對計算或模擬過程的精度要求較高,當需要研究的參數數量眾多時,有限差分法將需要較高的實施成本。

1.2 微分法

將式(1)擴展為狀態空間形式[15]

(7)

其中

記風速U處系統矩陣A的特征值和特征向量分別為Λ和Γ,即特征值λi=-ξiωi±iωi對應于特征向量

(8)

易知λi為式(1)的復特征值,而ψi則為式(1)右特征向量。

假定橋梁顫振影響因子β,則系統的特征值、特征向量、顫振臨界風速及系統矩陣均為β的函數。對于自激力作用下的橋梁結構第i階模態,有

P(λi(β),Uc(β),β)ψi(β)=0

(9)

系統矩陣A的左特征向量Π滿足

ΛΠT=ΠTA

(10)

其中

由式(10)可得橋梁結構的第j階模態滿足

(11)

(12)

(13)

文獻[16]對模態正交條件采用Taylor展開獲取模態規格化條件,此處對式(13)同樣采用Taylor展開,并減去式(12)后可得

(14)

對第i階模態,式(14)中i=j,括號內的表達式簡化為?P/?β|λ=λi,取左右特征向量使其滿足規格化條件

(15)

考慮影響因子β對系統的影響,對i階模態振動方程式(9)求β的導數

(16)

(17)

當系統處于顫振臨界狀態時,發散模態的特征值實部Re(λi)=0,因此對于橋梁顫振發散模態有如下實部和虛部方程

(18)

(19)

式中,Re()、lm()分別表示復數的虛部和實部。聯合求解式(18)、式(19)便可得敏感性dUc/dβ及dωi/dβ。

式(18)和(19)聯合求解時,發現Scanlan自激力模型是U的隱函數,無法直接求解?P/?Uc。風洞試驗表明,U通過顫振導數改變系統狀態,即系統矩陣A是U的函數,為求得?P/?Uc引進工程上常用的Roger有理函數近似顫振自激力,即

(20)

(21)

2 結構參數影響

影響橋梁顫振臨界風速的結構參數主要包括模態質量、阻尼比和固有頻率。由式(9)有

(22)

(23)

(24)

3 氣動參數影響

基于橋梁有限元模型,求廣義氣動剛度和氣動阻尼矩陣的偏導數?As/?β、?Ad/?β

(25)

(26)

4 大跨度橋梁三維顫振敏感性分析

本章首先針對經典薄平板簡支梁橋[17]開展三維顫振敏感性分析,對比有限差分法及參數化分析方法,以評估本文方法的精度和效率。在此基礎上,針對一座主跨918 m的雙塔三跨懸索橋開展顫振敏感性分析,研究橋梁結構參數和氣動參數對實橋顫振性能的影響規律。

4.1 理想薄平板簡支梁橋三維顫振敏感性分析

具有薄平板斷面的簡支梁橋結構參數如表1所示。選取前10階模態進行多模態耦合顫振分析,相關模態特性如表2所示。

表1 理想薄平板簡支梁結構參數Tab.1 Structural characteristics of the simple supported beam with an ideal thin flat section

表2 簡支梁前10階模態振型特性Tab.2 Modal characteristics of the first 10 modes of the simple supported beam

薄平板斷面的顫振導數由Theodorsen函數及準定常準則確定[18]。

多模態耦合顫振計算結果表明簡支梁的顫振臨界風速為143.9 m/s,與文獻[17]的研究結果吻合。在迭代過程中,對于每一級風速Ui均計算系統特征值的敏感性,用于預測下一級迭代風速Ui+1對應的系統振動頻率和阻尼比,預測結果與數值迭代結果對比如圖1所示,圖中實線代表數值迭代結果,散點表示預測結果,表明二者吻合較好。

(a) 振動頻率

(b) 阻尼比圖1 簡支梁顫振分析結果比較Fig.1 Comparison of flutter analysis of ratios of the simple supported bridge

圖2給出了顫振臨界風速對各階模態參數的敏感性dUc/dβi,橫坐標表示模態階數,dUc/dβi>0表示增大參數βi將提高顫振臨界風速Uc,反之dUc/dβi<0則表示增大βi將降低顫振臨界風速Uc。由圖2可知簡支梁的顫振臨界風速主要對1-S-V和1-S-T的模態參數敏感,而其它模態的參數變化對Uc的影響十分微弱。結合圖1(b)可知,1-S-T為簡支梁的顫振發散分支,圖2表明顫振臨界風速對1-S-T的3個模態參數的敏感性均大于1-S-V對應的模態參數,即該簡支梁的顫振發散分支1-S-T的模態參數對橋梁顫振的影響最顯著。此外,顫振臨界風速對阻尼比最敏感,對模態頻率和模態質量的敏感性則大致基本相當。由dUc/dβi的符號可知,增大各模態的阻尼比和模態質量均會提高顫振臨界風速。各模態頻率對顫振臨界風速的影響則不一致,增大一階扭轉頻率將提高顫振臨界風速,而增大一階豎彎頻率則導致顫振臨界風速降低。綜合豎彎和扭轉頻率的影響來看,增大基礎扭彎頻率比將提高顫振臨界風速。

圖2 簡支梁顫振臨界風速對結構模態參數的敏感性Fig.2 Sensitivities of critical flutter wind speed with respect to the simple supported beam modal dynamic characteristics

基于簡支梁結構參數敏感性,可預測相關模態參數發生一定變化時簡支梁的顫振臨界風速。表3對比了本文微分法預測結果和有限差分法、參數化分析方法的計算結果,表明當模態質量和頻率的變化幅度在±5%的范圍內、結構阻尼比的變化范圍在0～200%時,本文微分法預測結果與有限差分法及參數化分析結果均吻合較好。

表3 模態參數小幅攝動時簡支梁顫振臨界風速Tab.3 Critical flutter wind speed of simple supported beam with perturbed modal characteristics

圖3 簡支梁顫振臨界風速對顫振導數的敏感性Fig.3 Sensitivity of critical flutter speed with respect to simple supported beam flutter derivatives

表4 顫振導數攝動時簡支梁顫振臨界風速Tab.4 Critical flutter wind speed of simple supported beam with perturbed flutter derivatives 單位:m/s

為對比本文微分法和有限差分法進行敏感性分析的計算效率,分別統計了兩種方法進行簡支梁顫振敏感性分析的計算耗時,如表5所示。分析所用的計算機配置為i7-8560U CPU、16 GB內存。考慮到計算機系統因素對單次計算時間可能造成浮動的現象,表中所給的計算時間均為10次分析的平均計算時間。

表5 簡支梁顫振敏感度分析耗時Tab.5 Time consumed by flutter sensitivity analysis of simple supported beam

表5中:第⑤欄為采用本文微分法分析簡支梁所有結構參數和氣動參數敏感性所需時間。第⑥欄中npoint為單個參數采用有限差分法計算敏感性需要參數化計算的次數,由式(6)可知,采用一階前向差分格式計算每個參數的敏感性時npoint取2;npara為待研究的參數數量,本例共有45個,其中10階模態共30個結構參數,非零氣動參數15個。

表5的⑤和⑥兩欄對比結果表明,當選取合適的風速步長時,本文微分法的平均計算時間顯著小于有限差分法。分析可知,微分法只需要一次顫振分析和一次偏微分求解便能得到所有參數的敏感性;而有限差分法需要進行兩次參數化運算才能得到一個參數的敏感性,由此導致其在處理多模態耦合的橋梁顫振系統時,由于有較多的結構模態參數需要評估,導致有限差分法相對于本文微分法存在計算成本和時間成本劣勢。

4.2 大跨度懸索橋三維耦合顫振敏感性分析

以圖4所示的雙塔三跨縱向全漂浮懸索橋為研究對象,該橋跨徑布置為264+918+365=1 547 m,主梁采用圖5所示的扁平鋼箱梁,相關結構參數如表6所示。通過有限元分析獲取該橋的動力特性,選取對耦合顫振有較大影響的8階模態進行顫振敏感性分析,相關模態動力特性如表7所示。

圖4 懸索橋跨徑布置Fig.4 Schematic description of the suspension bridge

圖5 成橋狀態加勁梁斷面圖Fig.5 Cross section of the stiffening girder in operation periods

表6 加勁梁截面主要參數Tab.6 Sectional parameters of the stiffening girder

表7 參與耦合顫振分析模態Tab.7 Selected modes to participate coupled flutter analysis

(a) 顫振導數

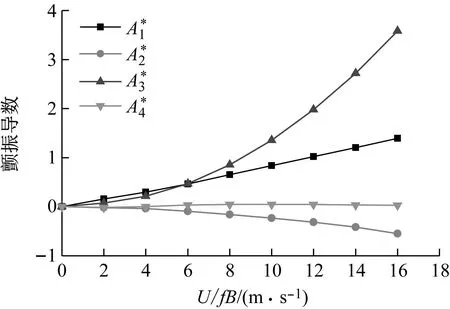
(b) 顫振導數圖6 加勁梁斷面顫振導數Fig.6 Flutter derivatives of the stiffening girder section

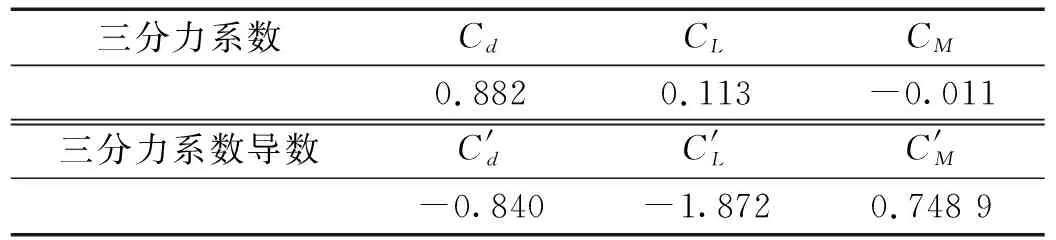
表8 加勁梁0°攻角三分力系數及其導數Tab.8 Force coefficients and their derivatives

該橋的耦合顫振分析結果如圖7所示。顫振臨界風速為85 m/s,顫振發散分支為1-S-T模態,對應于彎扭耦合扭轉分支顫振發散,基于特征值敏感性式(17)預測的各階模態阻尼比和振動頻率與數值迭代結果吻合較好。

(a) 振動頻率

b) 阻尼比圖7 懸索橋顫振分析結果比較Fig.7 Comparison of flutter analysis of ratios of the suspension bridge

圖8給出了該橋顫振臨界風速對各階模態參數的敏感性。對比圖2所示的簡支梁敏感性,兩橋的主導模態參數均為1-S-V和1-S-T模態參數,其中扭轉發散分支1-S-T模態參數的影響更突出;不同的是,該橋的1-A-V和2-S-V模態的動力特性參數對顫振臨界風速也有較大影響,表明該橋的模態耦合程度大于前述的簡支梁橋。各組模態參數按敏感性由高到低排序依次為阻尼比、模態頻率、模態質量。圖8的敏感性數值表明,增大阻尼比、模態質量及基礎扭彎頻率比均會提高顫振臨界風速。

圖8 懸索橋顫振臨界風速對結構模態參數的敏感性Fig.8 Sensitivities of critical flutter wind speed with respect to the suspension bridge modal dynamic characteristics

圖9 懸索橋顫振臨界風速對顫振導數的敏感性Fig.9 Sensitivity of critical flutter speed with respect to suspension bridge stiffening girder section flutter derivatives

5 結 論

本文基于直接微分法提出一種高效便捷的橋梁三維耦合顫振敏感性分析方法,旨在幫助設計人員在設計階段高效精準地獲取結構動力特性及顫振導數對大跨度橋梁顫振性能的影響規律。通過對理想平板斷面的簡支梁橋和采用流線型主梁斷面的懸索橋顫振敏感性分析發現:

(1) 在參與三維耦合顫振分析的橋梁多階模態中,顫振發散分支對應的模態參數對橋梁耦合顫振性能影響最大。對于采用理想薄平板、閉口鋼箱梁等流線型斷面的大跨度橋梁,一階對稱扭轉模態的動力特性參數對橋梁的顫振臨界風速的影響最顯著,一階對稱豎彎次之,而其它階模態參數的影響則相對較弱。

(2) 增大一階豎彎和一階扭轉模態的模態質量,結構阻尼比及基礎扭彎頻率均能提高橋梁結構的顫振臨界風速,但顫振臨界風速對各模態參數的敏感性差異較大,按敏感性由高到低排序依次為阻尼比、模態頻率和模態質量。