基于總安全系數法的噴射混凝土支護承載能力的試驗研究

肖明清, 徐 晨, 崔 嵐, 盛 謙, 陳 健, 謝壁婷, 吳 鵬

(1. 中鐵第四勘察設計院集團有限公司, 湖北 武漢 430063; 2. 水下隧道技術國家地方聯合工程研究中心, 湖北 武漢 430063; 3. 中國科學院武漢巖土力學研究所巖土力學與工程國家重點實驗室, 湖北 武漢 430071; 4. 中國科學院大學, 北京 100049)

0 引言

我國山嶺隧道以鉆爆法施工為主,結構形式一般采用噴錨支護復合式襯砌。其中,噴射混凝土作為初期支護最常用的支護方式之一,在控制圍巖變形、防止塌方破壞方面起到了重要作用[1]。

目前,學者們對隧道噴層的支護機制進行了大量的研究。根據經驗方法,李術才等[2]、馬棟等[3]依據多個實際隧道的施工實踐經驗,歸納總結施工期存在的各種不利地質條件,分析了支護結構體系包含噴層在內的力學行為特征。1)試驗方面: Fang等[4]、李榮錦等[5]開展了室內模型試驗,針對馬蹄形隧道施加初期噴-錨支護結構,對噴層、錨桿的承載能力與變形性能進行了探討;王亞威等[6]針對馬蹄形斷面隧道初期支護,將噴層與鋼拱架作為復合結構,開展了足尺結構試驗,分析了鋼拱架與噴層的承載能力與變形性能;宋遠等[7]為解決軟弱圍巖隧道在施工過程中容易出現支護不及時等問題,設計了空間網架支護結構,進行了該結構的足尺試驗,并對網架與噴層支護進行了闡述;來弘鵬等[8]基于隧道現場測試研究了圍巖壓力、格柵鋼架鋼筋應力、噴層和二次襯砌接觸壓力等變化規律及分布特性。上述試驗存在的不足主要有: ①對噴層的單獨承載能力研究不夠深入,噴層多數與錨桿、二次襯砌組合出現,且少有涉及噴層的破壞狀態; ②視噴射混凝土為獨立承載結構,忽略了噴層與圍巖的相互作用關系。2)數值計算方面: 崔嵐等[9-10]、楊林霖等[11]分別依托中條山隧道、華麗高速隧道,采用有限差分軟件探究了噴層接觸壓力與變形在開挖過程中的變化規律,并與現場監測數據進行了對比分析,為噴層支護設計參數的合理選擇提供參考;謝金池等[12]利用有限差分軟件揭示了不同隧道模式以及洞型對支護和噴層結構應力特性的影響機制;Chang等[13]采用有限差分方法模擬隧道約束收斂法中噴層對圍巖的約束能力,闡述了噴層在隧道縱向方向的受力與變形分布規律。3)理論方面: Sun等[14]在考慮超前支護的前提下,提出了支護和圍巖作用全過程的分析方法,通過平面應變分析得到隧道位移和初期支護沿隧道軸線的反作用壓力;Cui等[15-16]、Shen等[17]提出隧道二階段分析方法,給出針對應變軟化圍巖與支護作用的理論計算程序,可直接計算得到不同支護時機與剛度下噴層的支護效果與受力特征。

盡管上述學者針對隧道的噴層支護結構進行了大量的研究,仍存在下述不足: 1)噴層支護結構設計方面還沒有形成完備的理論與方法,仍然停留在“以工程類比為主、計算為輔”的階段,支護參數沒有明確的安全系數值,設計中隨意性很大,缺乏科學性; 2)尚無與實際較符合的單獨的噴層計算理論模型,難以進行“噴層結構”的量化設計。

近年來,肖明清等[18-23]、徐晨等[24]在系統總結國內外隧道設計理論與方法的基礎上,對我國隧道支護結構設計方法中存在的主要問題進行系統剖析,將現代數值分析方法與傳統荷載結構模型分析方法的優點相結合,形成了隧道支護結構設計總安全系數法,其中給出了明確的噴層等支護結構的計算模型。目前,總安全系數法重點進行了相關設計理論研究,尚缺少模型試驗的驗證,有待進一步研究深化。

本文設計大型隧道結構模型試驗系統,制備圍巖和噴層材料,開展不同厚度噴層的隧道模型加載試驗。通過噴層破壞全過程分析,并結合圍巖和噴層的受力監測數據,量化分析噴層設計承載能力。根據噴層荷載結構模型,得到基于總安全系數法理論的噴層設計承載力。通過對比分析模型試驗與總安全系數法理論條件下2種厚度噴層的設計承載能力,驗證噴層結構設計方法的合理性。

1 隧道支護結構設計總安全系數法

總安全系數法的核心內容包括: 1)提出采用圍巖壓力設計值來解決實際施工中圍巖壓力不確定問題的思路,并提出了圍巖壓力設計值的計算方法[18,24]。2)建立噴層、錨巖承載拱和二次襯砌的計算模型用于安全系數的計算[21]。3)提出復合式襯砌的總安全系數計算方法,并采用噴層-二次襯砌復合結構承載力計算模型對總安全系數計算方法的合理性進行分析[22]。4)提出支護結構總安全系數的取值建議[23]。

隧道噴層結構采用荷載結構模型進行內力計算,如圖1所示,在得到圍巖壓力設計值q后,根據q和設定的側壓力系數計算得到水平荷載e。噴層采用梁單元模擬,結構與地層相互作用通過設置無拉徑向彈簧和切向彈簧模擬,彈簧剛度根據圍巖條件選取。求得噴層的內力后,結構安全系數K按TB 10003—2016《鐵路隧道設計規范》采用破損階段法進行計算,計算如式(1)[25]所示。

KN≤φαRabh。

(1)

式中:K為安全系數;N為軸向力;φ為構件的縱向彎曲系數,對于隧道噴層取1.0;α為軸向力的偏心影響系數;Ra為混凝土或砌體的抗壓極限強度;b為截面的寬度;h為截面的厚度。

當噴層結構控制截面達到破損狀態時(安全系數等于1.0),假設其可以維持破損階段的承載力,并將破損區域的內力作為邊界條件施加在破損位置,再繼續增大荷載,直至出現第2個控制截面破壞時作為結構的極限承載力,其計算模型如圖2所示。

(a) 大偏心受壓破壞 (b) 小偏心受壓破壞

2 模型試驗方法

2.1 模型試驗系統設計

為了驗證總安全系數法理論,設計了大型隧道支護結構承載能力模型試驗系統。試驗系統主要由反力架、模型箱和液壓千斤頂組成,正面設有玻璃觀察窗,如圖3所示。模型臺架總體尺寸為4.10 m×0.99 m×3.80 m(長×寬×高),內含尺寸為2.5 m×0.45 m×2.3 m(長×寬×高)的模型箱。液壓千斤頂設2套液壓油源,可實現左右與上部千斤頂獨立伺服加載,最大荷載為1 MPa。

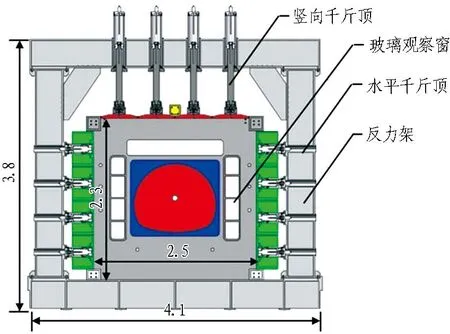
圖3 模型試驗系統示意圖(單位: m)

本試驗以速度為350 km/h的高鐵雙線隧道結構斷面為模擬對象,斷面外輪廓高度為12.1 m,跨度為14.6 m。區別于一般巖土試驗,本試驗為結構試驗,通過加載試驗手段,獲取支護結構在破損階段的承載能力和力學行為,并驗證其設計方法。在試驗設計時,幾何相似比取12.5,即試驗中隧道外輪廓斷面寬1.17 m,高0.97 m,圍巖、支護結構等基本物理力學參數按照相似第二準則進行確定。但本試驗的顯著特征為結構試驗,因此在試驗與理論計算結果對比分析時,均以模型試驗的具體工況作為研究對象,不按照相似準則進行換算分析。

2.2 模型試驗材料與力學參數

試驗時模型箱內部結構如圖4所示。為便于量化噴層與二次襯砌對圍巖的主動支護作用(提供σ3),試驗中將圍巖直接填筑形成拱結構,厚度為36 cm,拱結構外圍用傳力的細砂填筑,將千斤頂的荷載傳遞到拱結構上。

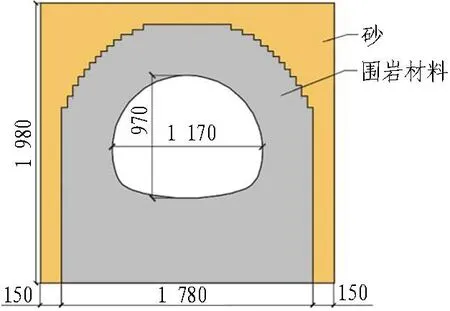
圖4 模型箱內部結構(單位: mm)

2.2.1 圍巖材料

圍巖的模擬材料主要采用重晶石、河砂以及粉煤灰作為骨料,并添加松香酒精溶液和機油提高材料的黏結性能。質量配比為重晶石∶河砂∶粉煤灰∶機油∶松香酒精=12.6∶6.3∶4.75∶1.5∶1。針對圍巖材料制備直徑為50 mm、高為100 mm的標準圓柱體試樣和直徑為61.8 mm、高為20 mm的恒重環刀樣,分別開展單軸抗壓強度試驗與直剪試驗,從而得到圍巖材料的物理力學參數。圍巖材料應力-應變曲線如圖5所示。圍巖材料τ-σ擬合直線如圖6所示。模型試驗材料物理力學參數如表1所示。

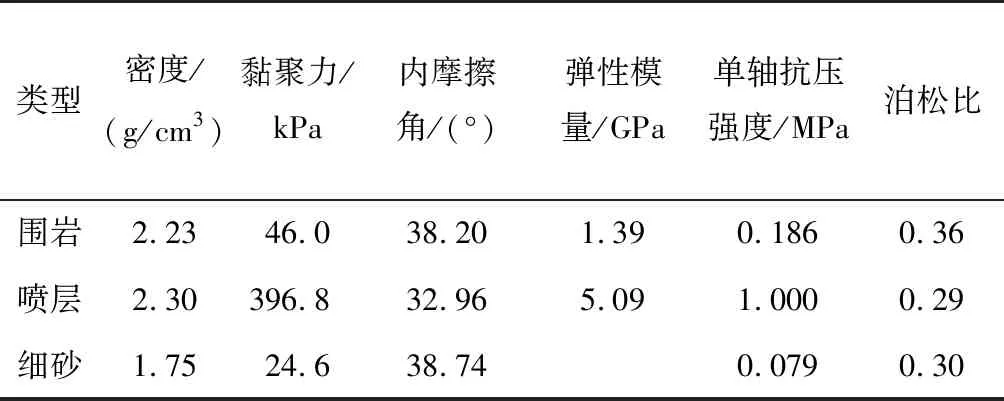
表1 模型試驗材料物理力學參數

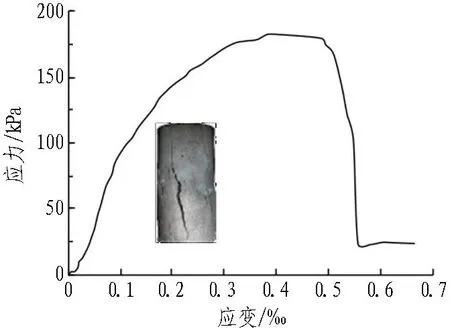
圖5 圍巖材料應力-應變曲線

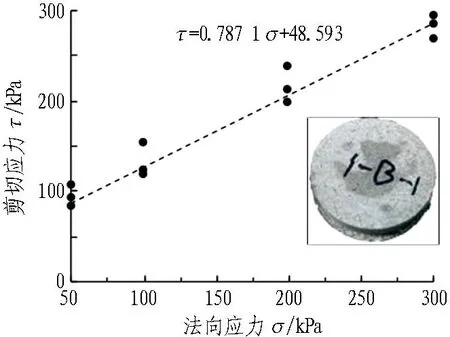
圖6 圍巖材料τ-σ擬合直線

2.2.2 噴層材料

噴層的模擬材料主要采用速凝石膏,混有重晶石與河砂,并摻入少量減水劑與甲基纖維素以增加材料的保水性和黏稠性。材料質量配比為重晶石∶河砂∶石膏∶水∶減水劑∶甲基纖維素=146∶36.5∶200∶81∶2∶1。

采用直徑為50 mm、高為100 mm的圓柱體試塊進行單軸試驗和三軸試驗,應力-應變曲線與最大主應力σ1-最小主應力σ3擬合直線如圖7和圖8所示,獲取的噴層模擬材料的各項力學參數見表1。

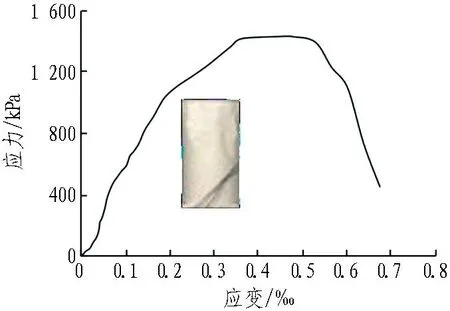
圖7 噴層材料的單軸加載試驗曲線

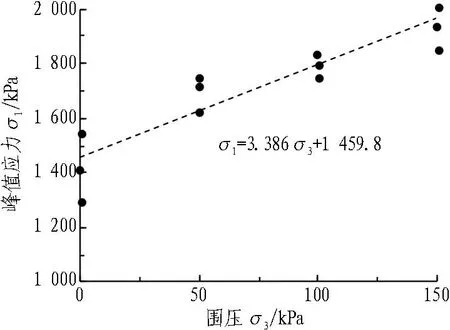
圖8 噴層材料σ1-σ3擬合直線

2.2.3 鋼絲網

噴層中掛有鋼絲網,鋼絲網采用304不銹鋼,網絲直徑為1 mm,網格間距為20 mm。

2.2.4 細砂

圓粒細砂作為傳力介質,為測定其具體物理力學參數,制備直徑為38 mm、高為76 mm的圓柱體試樣進行三軸試驗,應力-應變曲線與σ1-σ3擬合直線如圖9和圖10所示,得到的具體物理力學參數見表1。

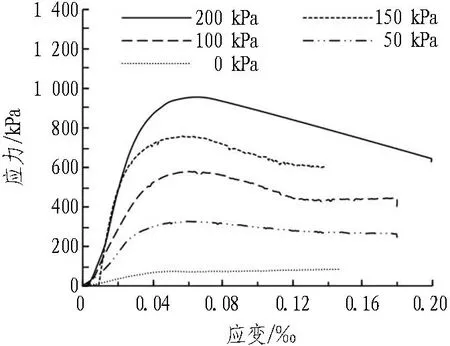
圖9 不同圍壓下傳力細砂的應力-應變曲線

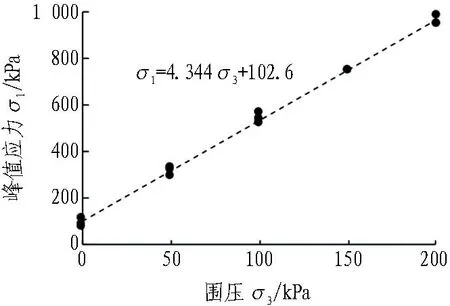
圖10 細砂σ1-σ3擬合直線

2.3 應變與位移監測系統

為能有效揭示圍巖及噴層的破壞規律,設計試驗監測系統,包括圍巖內部應力應變、噴層應力應變以及隧道位移。采用靜態信號測試分析儀進行連續采樣。

2.3.1 圍巖內部應力應變監測

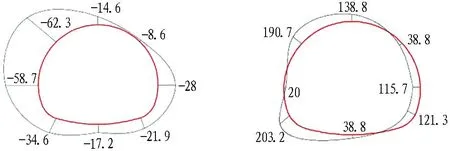
采用應變磚和土壓力盒進行圍巖內部應力應變監測。其中,應變磚采用圍巖材料制作,其上貼有應變花。沿隧道軸向0.225 m布設1個監測斷面,總計有27個土壓力盒、12個應變磚。監測布置如圖11所示。

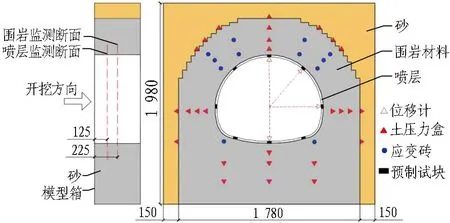
圖11 監測布置圖(單位: mm)

2.3.2 噴層內外應變監測

在隧道軸向0.125 m處布設1個斷面監測噴層內應變,如圖11所示。具體方法為: 采用噴層材料預制與噴層等厚的試塊,其內外兩側粘貼應變片(見圖12),預制試塊在噴層施作前固定于洞周,共設8個點位,然后采用噴層材料覆蓋。

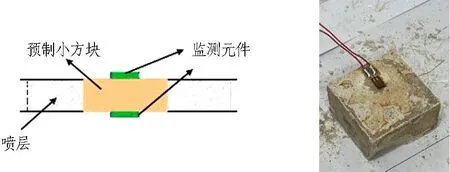
(a) 示意圖 (b) 實物圖

2.3.3 隧道位移監測

采用4個位移傳感器進行隧道位移監測,量程為0～30 mm,以向洞內收斂變形為正值,向洞外變形為負值,主要布置在拱頂、邊墻、隧底以及45°拱肩方向(見圖11)。

2.4 模型制作與試驗方案設定

2.4.1 圍巖填筑

制作模型時,分層填筑夯實,每層高度約為5 cm。為減小圍巖材料、細砂與箱體之間的摩擦力,在箱體內壁涂抹黃油。為便于夯實,以階梯型近似模擬拱形,當填筑至拱墻略高處時,分13級臺階填筑,踢面高為4 cm,踏面寬4～8 cm。

2.4.2 隧道成型

本試驗為非開挖試驗,不考慮施工方法的影響,在圍巖填筑之前預先放置與隧道大小一致的柱形高強泡沫模具,圍巖填筑完成后,放置12 h,待圍巖略干,用熱風槍將泡沫模具融化,隧道成型,毛洞制作完成。

2.4.3 噴層制作

隧道成型后開始制作噴層結構。由于圍巖材料中含有粉煤灰,在其表面直接涂抹噴層材料比較困難。先用注射器沿隧道環向噴1圈稀石膏液,使隧道表面盡量光滑,防止脫模后材料掉落;然后沿隧道環向支撐鐵皮作為模板,并與圍巖之間留有2 cm空間用于填充噴層材料,逐層填充材料后,待流動性基本喪失,但材料尚未完全固化,拆除鐵皮模板,掏出孔洞埋置監測元件,等待徹底固化,噴層成型。

2.4.4 二次襯砌制作

首先,在塑料薄膜上涂抹黃油,使塑料薄膜粘附于圍巖表面,模擬防水層;然后,沿隧道環向支撐鐵皮作為模板,并與圍巖之間留有4 cm空間用于填充二次襯砌材料,待材料固化后,拆除鐵皮模板,二次襯砌成型,厚度為4 cm。

2.4.5 方案設定

考慮3種試驗工況,即毛洞工況、2 cm噴層工況和4 cm噴層工況,分別設置為工況1、工況2、工況3。為研究噴層與圍巖界面粘結效應對承載力的影響,另外設計了工況4,即二次襯砌工況,該工況的襯砌厚度為4 cm,材料與噴層相同,但在二次襯砌與圍巖之間設置了塑料隔離層。

2.4.6 試驗加載

結合實際工程情況與TB 10003—2016《鐵路隧道設計規范》,考慮側向荷載與豎向荷載的比例為0.44。為準確獲取支護結構的承載能力,采用逐級加載的方式,豎向荷載從50 kPa開始施加,每級增加20 kPa;橫向荷載從22 kPa開始施加,每級增加約8 kPa,每級荷載維持20 min,直至隧道完全垮塌。

3 模型試驗結果分析

3.1 承載能力定義及其對應的結構狀態

為便于分析,本文對毛洞、噴層和二次襯砌各結構的承載能力及其對應的結構狀態進行了定義。

將毛洞僅出現局部坍塌的前1級荷載,定義為毛洞設計荷載;將毛洞發生整體垮塌的前1級荷載,定義為毛洞極限荷載。

將噴層或二次襯砌出現第1條裂縫時的前1級荷載,定義為結構設計荷載;將整體結構發生整體垮塌的前1級荷載,定義為結構極限荷載。

將結構與毛洞的設計荷載之差作為“結構設計承載力”,與最不利截面安全系數K=1相對應;將結構與毛洞的極限荷載之差作為“結構極限承載力”。

3.2 破壞狀態與破壞荷載

4種工況的破壞特征演變如下所述。

工況1: 毛洞試驗工況下,當豎向荷載達到90 kPa時,右拱肩位置處圍巖發生壓剪破壞,局部小范圍掉塊,形成楔形破壞區;當豎向荷載達到150 kPa時,拱頂一定深度圍巖出現突然坍塌并與左右拱肩的坍塌區貫通(見圖13),其前1級荷載(130 kPa)即為毛洞設計荷載;當繼續加載至170 kPa時,毛洞整體垮塌,其前1級荷載(150 kPa)即為毛洞極限荷載。

(a) 現場試驗圖 (b) 破壞示意圖

工況2: 2 cm噴層工況下,當豎向荷載達到250 kPa時,左拱肩噴層處出現較明顯剝落,鋼絲網扭曲狀(見圖14(a)),判定為達到設計荷載狀態,取230 kPa為結構設計荷載;繼續加載至350 kPa時,發生整體垮塌,取其前1級荷載(330 kPa)作為結構極限荷載。

(a) 2 cm噴層250 kPa (b) 4 cm噴層290 kPa

工況3: 4 cm噴層工況下,破壞過程與工況2基本相同。當豎向荷載達到290 kPa時,左拱肩噴層處出現較明顯剝落(見圖14(b)),判定為達到設計荷載狀態,取270 kPa為結構設計荷載;繼續加載至530 kPa時,發生整體垮塌,取其前1級荷載(510 kPa)作為結構極限荷載。

工況4: 二次襯砌工況下,當豎向荷載達到270 kPa時,二次襯砌出現破裂,有明顯裂縫(見圖15),取250 kPa為結構設計荷載。當豎向荷載為430 kPa時,整體坍塌。因此結構極限荷載為410 kPa。

圖15 二次襯砌破壞現象(270 kPa)

上述試驗結果及結構設計承載力如表2所示。

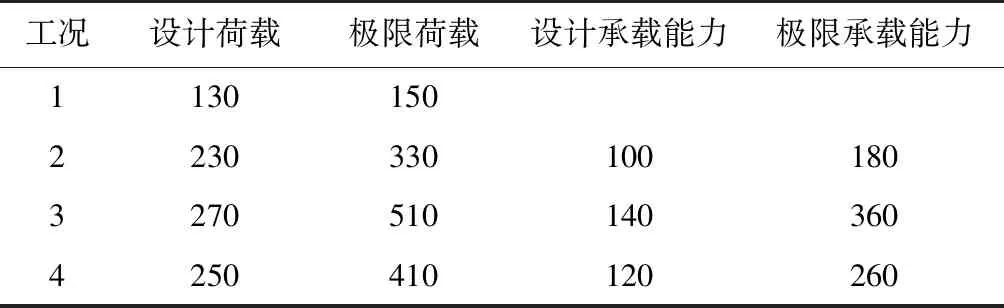
表2 噴層試驗承載力

3.3 噴層變形與受力特征

3.3.1 隧道位移

前3種工況下拱頂位移與載荷的關系如圖16所示。由圖可知: 1)在相同荷載下,毛洞位移最大,噴層厚度越大位移越小; 2)3種工況的隧道最大位移分別為4、25、34 mm,說明噴層厚度增大,提高了隧道圍巖與噴層整體結構的延性。

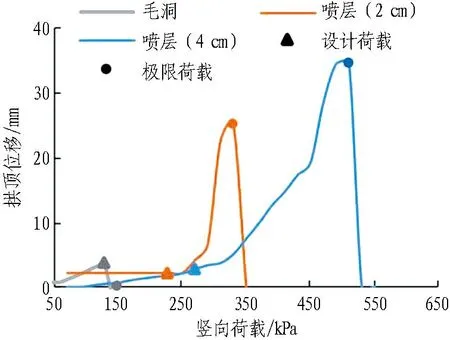
圖16 噴層拱頂位移

3.3.2 圍巖(拱)應力

隧道的圍巖徑向(小主應力)和切向(大主應力)應力變化曲線如圖17和圖18所示。

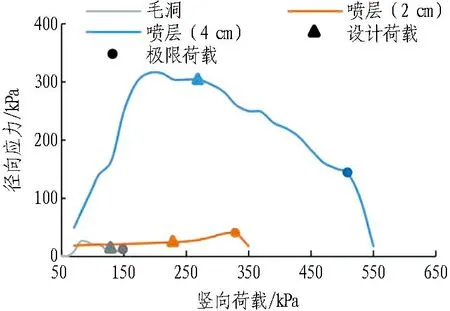
(a) 拱肩13 cm處

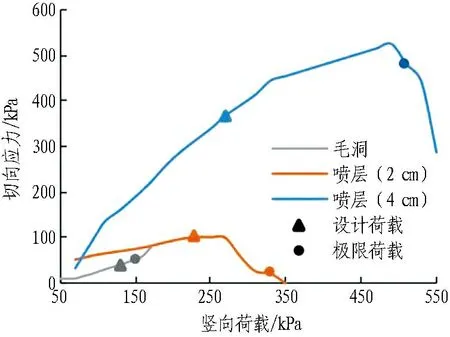
(a) 拱肩13 cm處

由圖17可知: 對于拱肩位置,在同一試驗荷載下,以130 kPa為例,2 cm噴層工況的圍巖徑向應力較毛洞提高了49.5%;4 cm噴層工況的圍巖徑向應力較毛洞提高了9.8倍。由圖18可知: 1)2 cm噴層工況的圍巖切向應力較毛洞提高了81.3 %; 4 cm噴層工況較毛洞提高了3.2倍。2)對于拱頂位置,2 cm與4 cm厚度噴層徑向應力分別為毛洞的1.73倍和4.95倍,切向應力分別為毛洞的1.66倍和25.79倍。以上說明,噴層厚度越大,洞周圍巖的切向應力越大,隧道的成拱效應越顯著;噴層厚度越大,圍巖的徑向應力也相應增加,進而提高了圍巖強度和圍巖的自承載能力。

3.3.3 噴層內力

噴層內力由設計荷載下的噴層內外側應變監測值計算得到,軸力與彎矩的計算公式分別如式(2)和式(3)所示。

(2)

(3)

式(2)—(3)中:N和M分別為噴層的軸力與彎矩;E為噴層彈性模量;ε內和ε外分別為噴層內外側應變;b為單位長度,取單位1;h為噴層厚度。

設計荷載下噴層內力如圖19所示。由圖可知: 無論2 cm厚度還是4 cm厚度,噴層受力以軸壓為主,彎矩很小,軸力最大處均位于左拱肩,噴層破壞時表現為壓潰破壞。由此可見,由于噴層與圍巖粘結,二者之間可傳遞剪力,從而將圍巖傳遞至噴層的荷載主要轉化為噴層軸力,噴層處于小偏心受壓狀態,進而充分發揮材料強度和承載能力。

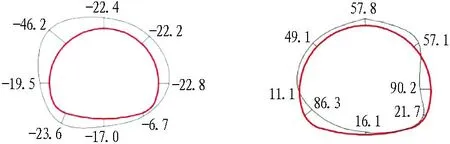
(a) 2 cm噴層軸力(單位: kN) (b) 2 cm噴層彎矩(單位: N·m)

3.4 二次襯砌受力及其承載力

3.4.1 二次襯砌工況位移

二次襯砌工況與4 cm噴層工況拱頂位移如圖20所示。由圖可知: 1)在結構達到設計承載能力前,在相同的豎向荷載下,噴層工況的位移相對較小; 2)二者極限位移基本相同,約為34 mm。

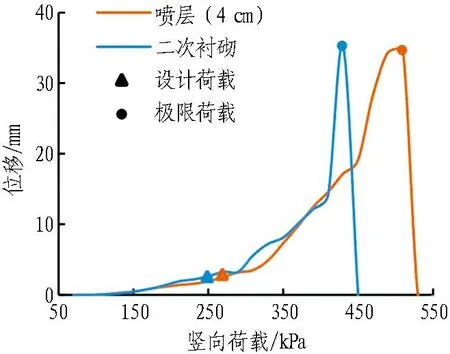
圖20 拱頂位移

3.4.2 二次襯砌工況圍巖應力

隧道拱肩外側約13 cm處的圍巖徑向(小主應力)和切向(大主應力)應力變化曲線如圖21和圖22所示。由圖21和圖22可知: 相同荷載下噴層工況圍巖的徑向應力和切向應力顯著大于二次襯砌工況,說明噴層與圍巖之間的剪切效應能更好地發揮噴層的作用,提供更大的支護力。

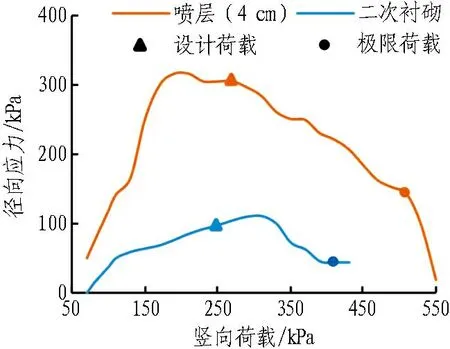
圖21 二次襯砌拱肩13 cm處圍巖徑向應力

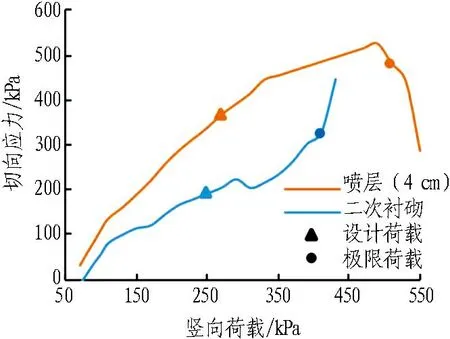
圖22 隧道拱肩13 cm處圍巖切向應力

3.4.3 二次襯砌內力

設計荷載(250 kPa)下二次襯砌的內力如圖23所示。由圖19(c)和圖23(a)可知,在相同厚度4 cm下,二次襯砌所受軸力明顯小于噴層所受軸力,偏心距較噴層工況略有增加。

(a) 軸力(單位: kN) (b) 彎矩(單位: N·m)

3.4.4 噴層與二次襯砌承載力試驗值對比

由于噴層與圍巖之間能夠傳遞剪力,而二次襯砌與圍巖之間不傳遞剪力,因此在相同厚度情況下,噴層的承載力要高于二次襯砌承載力,相同厚度噴層的設計承載能力和極限承載能力分別比二次襯砌工況高16.7%、38.5%。

4 模型試驗與理論計算結果對比

4.1 設計承載能力計算值

由于噴層背后為圍巖和傳力細砂組成的復合地層,彈性抗力系數難以采用試驗方法直接獲取,故采用三維有限差分軟件建立計算分析模型,模型尺寸與參數均與模型試驗一致,在洞周施加均布徑向荷載q(本計算取100 kPa),計算邊墻部位的變形值Δu,則彈性抗力系數k按照式(4)計算,可得彈性抗力系數為310.63 MPa/m,切向抗力系數取徑向抗力系數的1/3。

(4)

根據第1章節所述計算方法,建立相應的荷載結構模型,可以得到噴層安全系數K=1時的設計承載力。

由于在噴層支護下,外側圍巖拱的承載能力相應提高,其提高部分也需要計入總承載能力提高值。將外側圍巖拱采用梁單元模擬,圍巖拱與地層相互作用徑向采用無拉彈簧模擬,墻腳處采用豎向和水平向彈性支撐模擬。采用現行《鐵路隧道設計規范》破損階段法進行安全系數計算,取安全系數等于1時的承載能力記為圍巖拱的設計承載能力。圍巖拱在噴層作用下的計算模型如圖24所示。

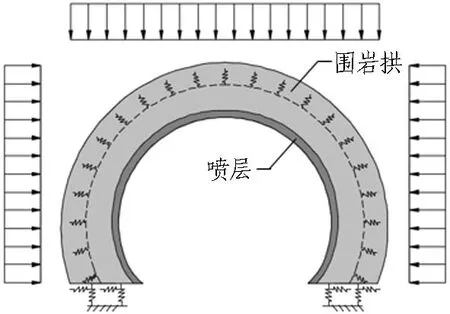
圖24 圍巖拱在噴層作用下的計算模型

圍巖拱在噴層支護抗力作用下強度提高,其抗壓強度σc按式(5)計算。

(5)

式中: [σc]為圍巖的極限抗壓強度;c為承載拱圍巖采用錨桿加固后的黏聚力;φ為承載拱圍巖的內摩擦角;σ1為最大主應力;σ3取噴層的承載能力計算值的50%(主要考慮接觸力的不均勻性和剪應力對圍巖強度降低效應)。

分別計算工況2、工況3圍巖拱的承載能力,與σ3=0時的計算結果差值可以記為工況2、工況3的圍巖拱承載能力提高值。疊加噴層的承載能力和圍巖拱的承載能力提高值即為理論計算的設計承載能力。試驗結果與理論計算結果如表3所示。

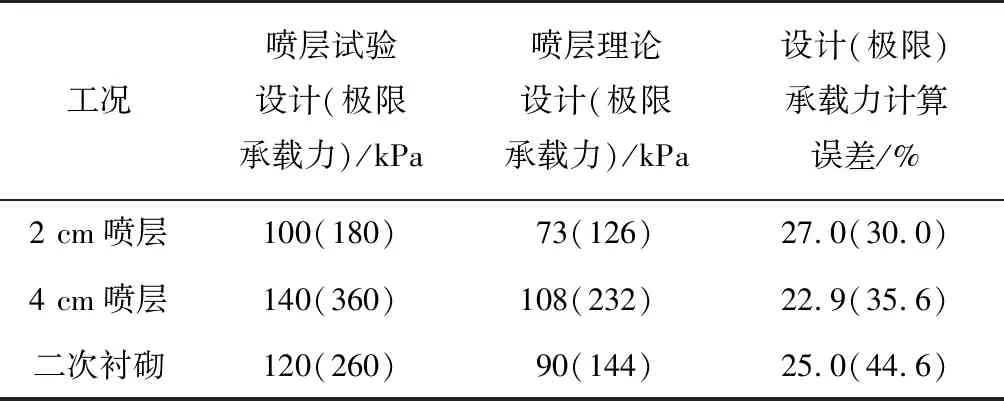
表3 設計荷載下試驗結果與理論結果對比

4.2 噴層的承載能力對比

由表3可知: 1)2 cm噴層的理論結果比試驗設計承載力小27.0%,4 cm噴層的理論結果比試驗設計承載力小22.9%。2)2 cm噴層與4 cm噴層試驗結果均比理論結果大,且理論與試驗結果的差別較小,表明總安全系數法噴層計算模型可以表征實際的承載能力,并具有一定的安全余量。

4.3 噴層內力分布對比

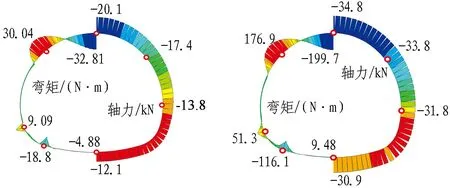
噴層以小偏心受壓為主,彎矩較小,因此主要對噴層的軸力進行對比。具體理論計算結果如圖25所示,由于內力都是對稱分布,在圖中將彎矩繪于隧道左半部分,軸力繪于隧道右半部分。對比試驗結果與理論結果(見圖19與圖25),從軸力分布形態上看,試驗得到的最大軸力位于拱肩,而理論最大軸力位于拱頂,雖稍有差別,但兩者均在拱部區域內(試驗中受各種因素影響,軸力不對稱),并且軸力從拱肩往拱腰直至拱底均呈現減小趨勢,總體分布特征較為吻合。

(a) 2 cm噴層 (b) 4 cm噴層

在內力量值方面,考慮到試驗中受各種因素影響,軸力不對稱,為便于與理論計算結果進行對比,取拱部區域試驗值的平均值作為軸力試驗值。由圖19(a)和圖25(a)可以看出,2 cm噴層工況下,拱部軸力試驗值為30.3 kN(拱頂與左右拱肩平均值),理論計算結果拱頂為20.1 kN,拱肩為17.4 kN,試驗結果分別比理論結果大33.7%和42.6%。4 cm噴層工況如圖19(c)和圖25(b)所示,拱部軸力試驗值為124.8 kN(拱頂與左右拱肩平均值),理論計算結果拱頂為34.8 kN,拱肩為33.8 kN,試驗結果比理論結果分別大72.1%和72.9%。

通過上述對比可知,試驗與理論計算得到的2種厚度噴層的內力雖然在量值上存在一定的誤差(主要受噴層結構應變監測精度等因素影響),但分布特征基本相符,且破壞特征均表現為拱部的受壓破壞。說明總安全系數法理論可以較為準確地反映噴射混凝土支護的破壞特征和承載能力,且具有一定的安全余量。

5 結論與討論

1)噴層與圍巖之間的密貼和粘結是發揮噴層承載能力的關鍵,其徑向和切向作用可分別采用徑向彈簧(無拉)和切向彈簧模擬。噴層受力狀態為小偏心受壓,能充分發揮材料的抗壓強度,提高支護承載能力。試驗中,噴層的設計承載力與極限承載力比二次襯砌分別提高了16.7%和38.5%。

2)2 cm噴層工況與4 cm噴層工況的設計承載力試驗值比總安全系數法理論結果分別高出27.0%、22.9%,表明總安全系數法的噴層計算模型可以表征實際的承載能力,并具有一定的安全余量。

3)從噴層軸力形態方面看,試驗與理論計算結果總體分布特征較為吻合。從噴層軸力量值方面看,試驗與理論計算結果在拱部區域較為接近,且試驗結果小于理論結果,表明總安全系數法在噴層(或二次襯砌)本身的理論承載力計算方面是合理的。

需要說明,本試驗為結構加載試驗,隨著荷載逐步增加,因噴層受力導致的圍巖的σ3也逐漸加大,進而提高了圍巖的自承載力,因而承載力計算值與試驗值比較時,需要考慮圍巖自承載力的提高值。而實際隧道開挖為卸載過程,隨著圍巖變形的增加,圍巖的σ3逐漸減小,直至與噴層支護抗力實現平衡,因此,實際隧道的噴層(無錨桿支護)承載力計算時,不應計入因噴層提供σ3后圍巖的承載力增加值。

本文開展了大尺寸隧道模型試驗,與以往小尺寸隧道模型試驗相比能更好地再現破壞過程,獲取支護結構在承載過程中的受力,了解噴層支護的承載特性,從而較好地驗證總安全系數法理論。但試驗結果與理論結果也存在一定差異,由于理論計算參數是基于室內試驗測試得到的,在實際模型試驗過程中受氣候、人為等多方面因素影響,實際材料的參數可能與室內試驗獲得存在差別,因此試驗結果并未與理論結果完全吻合。后續研究將進一步考慮多層支護結構形式(如噴錨組合支護、復合式襯砌支護)下的承載特性,以期系統地驗證總安全系數法理論,為隧道支護結構設計提供相關指導。