習題教學功能之拓展數學認識和題型見識

［摘 要］小學數學中的例題不可能涵蓋所有的知識點，所以有一些知識需要安排在習題中進行教學。數學習題千變萬化，有些習題在長期的教學中被廣泛使用，逐漸成為針對某一數學知識而配備的經典習題。可見，依托習題教學可以拓展學生對數學的認識，也可以拓展學生對數學經典題型的見識，這些亦是習題教學的重要功能。

［關鍵詞］習題教學；功能；數學知識；題型

［中圖分類號］ G623.5［文獻標識碼］ A［文章編號］ 1007-9068（2024）12-0014-05

例題的主要功能是讓學生通過解答問題來學習新的知識或技能。那么，例題能把小學數學中的知識與技能全部涵蓋嗎？答案是否定的。在小學數學中，例題教學的是最基礎、最重要的知識與技能，還有基于例題的知識與技能而衍生出的相關的知識與技能，以及與此相關的一些題型，并沒有被編設成例題，而是蘊含在習題中。由此，小學數學習題教學便承載了新的功能。

一、拓展學生對數學的認識

具體討論習題教學在拓展學生對數學的認識這一功能之前，我們先來看一個案例。

案例1：異分母分數加減法

習題教學記：2019年5月27日，周一。

今天的數學課，我先反饋上一次作業的情況——學生在計算異分母分數加減法過程中出現的書寫規范問題；在明確了格式上的規范性之后，再讓學生以規范的格式寫了兩道習題，以加深印象，鞏固技能；然后出示[12] + [13]這一異分母分數加減法的算式，要求學生觀察后直接說出答案。在略作等待之后，一位學生站起來，猶猶豫豫地說出了[16]。我板書答案后，讓他解釋是怎么想的。在確認學生的解釋正確之后，我進行[13] + [14]的教學。

這次，我請了一位舉手的學生回答，她快速地說出了[112]。同樣是說算理后，進入下一題[14] + [15]的教學。舉手的學生一下子增加了許多，我知道有一些學生已經發現其中的奧秘了。我請一位學生回答，他快速地給出了正確的答案。我不再讓他說理由了，而是直接進行下一題的教學。

在我還在板書[15] + [16]的時候，已經有幾位學生迫不及待地喊道“我來！”“我來！”……等我寫完后，班級里就像炸開了鍋，連平時上課最愛開小差的××學生也把手舉得高高的。于是，我請他回答，結果他回答正確。

師：你們怎么越算越快了？（問題提出后，很多學生立刻舉起了手）

生1：只要把分母乘一下，就是分母；分母加一下，就是分子。

師：把這個特點再觀察、思考一下，為什么可以這樣算呢？（學生靜靜地思考著，慢慢地，有學生舉手了）

生2：因為這些分數的分母是互質數，所以分母就是它們的乘積，分子就是交叉相乘，這樣加一下就可以了。

這位學生的解釋顯然是正確的，只是表述含糊不清。于是，我再請一位學生表達自己的想法。最后，我以[15] +? [16]為例，結合板書，與學生一起再次理解其中的算理：[15] +? [16] = [1×65×6] + [1×56×5] = [6+55×6] = [1130] 。

第一步：通分。原來分數的分母互質，分母相乘做分母；原來分數的分子都是1，分母成了通分后分數的分子。

第二步：相加。和的分母相當于原來分數的分母相乘，和的分子相當于原來分數的分母相加。

……

以人教版數學教材為例，在案例1涉及的五年級“分數加減法”這一教學內容中，教材一共編排了4道例題，分別是“同分母分數加減法”的例1、“異分母分數加減法”的例1以及“分數加減混合運算”的例1、例2。這4道例題都不涉及案例1中所發現的知識，與此相關的“發現”出現在“異分母分數加減法”教學之后的練習二十四第6題中（見圖1）。

[?先計算，再想一想怎樣算比較快。]

圖1 人教版數學教材五年級下冊練習二十四第6題

類似于上述將某一數學知識蘊含在習題教學中的情況，在小學數學教學中是非常常見的。如學習平行四邊形、三角形的面積計算之后，教材會在后續的習題教學中引導學生發現“等底等高”的相關知識。由此可見，習題教學具有拓展學生數學認識的功能。這也正如波利亞所言：“一個重大的發現可以解決一道重大的題目，但是在解答任何一道題目的過程中都會有點滴的發現。”因此，作為一名小學數學教師，要善于理解和挖掘習題的內涵，精心設計習題的教學過程，帶領學生在解答習題的過程中去進一步發現，拓展學生的數學認知。

這個時候，我們自然會有這樣一個疑問：“為什么這樣的數學知識、技能不編排成例題呢？”原因是多方面的，以下兩點可以作為對此問題的回答。

第一，突出例題的代表性，控制例題數量。

例題中承載的知識或技能，往往是某一知識或技能的源點。通過這個源點，可以衍生出很多支流。在從源點衍生出的這些支流中，一些基礎的、重要的代表性支流中蘊含的知識或技能則可以再次編排成例題。如學習“乘法分配律”之后，應用乘法分配律進行簡便計算，一般有7種典型題型（見表1）。

對小學數學7個版本的教材進行統計分析后發現，沒有一個版本的教材將表1中的7種典型題型都編排為例題（見表2）。一方面，通過表2可以發現，在乘法分配律的7種典型題型中，例題編排率最高的是“34×72+34×28”型，有6個版本的教材編排了；例題編排率位于第二的是“（80+4）×25”型，有5個版本的教材編排了；例題編排率位于第三的是“32×102”型，有3個版本的教材編排了。可見，這3種題型是具有代表性的。其中，“34×72+34×28”型和“（80+4）×25”型的代表性體現在其基礎性上，即這2種題型是乘法分配律這個源點衍生出去的主干支流，因此編排為例題的必要性最高；而“32×102”型的代表性體現在其拓展性上，是具有代表性的一種典型題型，所以也有編排為例題的必要性。至于“107×34-7×34”型，雖然蘊含了乘法對減法的分配律這一新知識，具有拓展、完善學生對乘法分配律認識的功能，但因為這一知識只要基于乘法對加法的分配律的意義，就容易從“34×72+34×28”型中實現思維的正向遷移，因此不具有代表性，故7個版本的數學教材將這種題型均編排在習題中，而不編排為例題。至于“37×99+37”型和“99×49”型，同樣只要在習題中將例題知識實現遷移即可。

另一方面，如果把這些支流都編排為例題的話，那么教材上的例題會有很多，數學教材就會很厚，這顯然是不合適的。因此，只要將具有代表性的支流編排為例題即可，與此有一定關系的知識或技能，可在習題教學中讓學生進行遷移學習，這也是提升學生應用能力、創造性解決問題能力的一個重要途徑。

第二，知識點是一種拓展性認識，非“雙基”。

2023年春季，人教社數學1～6年級下冊全新插圖版教材正式使用。這套新插圖版教材除了插圖全部重繪，對部分內容的編排也進行了調整。如四年級下冊“小數的意義”單元，在學習了“小數點移動”之后，舊插圖版教材中編排了一道解決問題的例題（見圖2），并在這道例題之后的練習十一中編排了4道對應的解決問題習題。而在新插圖版教材中，圖2這道解決問題的例題被刪除了，同時刪除的還有練習十一中4道解決問題的習題。

[我用1萬元人民幣

可以換多少美元？][1元人民幣可以換

0.1563元美元。]

圖2 人教版（舊插圖版）數學教材四年級下冊“小數點移動”解決問題的例題

這在一定程度上反映出教材在例題與習題編排上的一個要求：數學教材中，編排為例題的知識或技能，一定是“雙基”的重要組成部分。但是，出現在習題中的數學知識或技能可以不是“雙基”，而是作為一種對例題知識學習之后的拓展性認識。如在上面的例子中，圖2作為例題出現，那么這個知識就是“雙基”，是要求所有學生都要掌握的，為此就有專門的習題用于練習鞏固。而在案例1中提到的異分母分數加減法的計算方法，因為出現在習題中，故不要求所有學生都要學會，理由是這種計算方法只是針對異分母分數加減法中的一類特殊題型才適用的簡便算法而已，這種計算方法學生會不會與能不能正確計算異分母分數加減法沒有關系。因此，這只是作為異分母分數加減法中的一種拓展性知識來認識，不是“雙基”。由此可見，類似于案例1中的拓展性知識，適合出現在習題中，而不適合編排為例題。

二、拓展學生對習題題型的見識

有一定教學經驗的小學數學教師在針對某一知識的習題教學中，會在合適的時機針對這一知識安排一些特定的習題題型。甚至有時候會有這樣一種感覺，如果在教學這一知識時沒有安排這種特定的習題題型，就會覺得這一知識沒有教學完整，學生難以理解與掌握這一知識。

案例2：除數是一位數的除法

習題教學記：2020年4月28日，周二。

課件出示習題：□63÷8，如果商末尾有0，那么□里可以填（? ?）。

師：怎樣才能使商末尾有0？（學生被這個問題難住了，略作等待之后，一位學生猶豫著舉手了）

生1：就是最后比除數小。

我理解這位學生的意思，但估計現在只有自己才是他的知音，其他學生肯定是一頭霧水。

師：也就是個位除不動，是不是這個意思？（生1點點頭）這到底是什么意思呢？我們來試試看。

我板書了如上的除法豎式，從最小的數開始，填入1試一試，得到下圖。

師：觀察一下，看明白了什么？

生2：最后的3比除數小。

此時，我知道有些學生對生1的說法有點理解了。于是，我和學生再一起邊看豎式邊理解。

師：對呀，將最后個位的數移下來，商不夠1，就只能是0了。這樣，商的末尾就有0了。

我把豎式寫完整，讓學生直觀地看到商末尾的0。但感覺這樣教學，還是不痛不癢，不是滋味，需要繼續觀察思考。

師：怎樣才能使個位上的數移下來還是不夠除呢？

很快就有學生舉手了，我知道這個時候學生對這道習題開始有點感覺了。于是，我依舊等待，等待更多的學生舉手。

生3：前面正好減去，沒有余數。

（這是很了不起的一步，但我裝作若無其事的樣子）

師：說說簡單，怎樣才能使前面正好減去而沒有余數呢？

學生先獨立思考，再同桌討論，最后全班一起交流，最終發現：只要8的乘法口訣中得數個位是6的情況就可以。于是，學生又想到了□中可以填5，這樣商是70，末尾有0，并填入2和6驗證是不行的。

從回答的情況看，學生填入1和5的情況比較多，當然兩個都填入的極少。不過，明眼人一定已經看到，這道習題還有一個答案——9。為什么學生能想到1和5，卻想不到9呢？因為8的乘法口訣中沒有得數是96的。

師：看來，這里可以填1，也可以填5。還有不一樣的答案嗎？（學生表示沒有了）我告訴大家，還有一個答案。（等待，等待……終于，一位學生舉手了）

生4：9。（學生自己嘗試，發現9是正確的）

在完成9的驗證之后，學生進一步討論：為什么我們都想不到9？

……

案例2中的習題“□63÷8，如果商末尾有0，那么□里可以填（? ?）”，相信教過“除數是一位數的除法”這一知識的教師一定不會陌生，因為這是習題中的一種經典題型。因此，當教學這一知識時，很多教師都會安排這樣的特定題型讓學生練習。這種題型后續還會出現在很多相關知識的習題中，如“除數是兩位數的除法”等。

計算教學的一個很重要目標，就是使學生能夠正確、靈活地進行計算。但是，類似案例2這樣的習題不是為了獲得一個正確的計算結果，而是為了鞏固學生對算理的理解和掌握，因此這種題型也會經常出現在檢測題中。這就是說，有時候為了檢測學生對某一數學知識是否全面、深入地理解和掌握，經常會有一些與這一目標相匹配的特定題型出現。經過長時間的發展，其中有一些特定題型已經成為經典題型。這種經典題型有時出現在例題中，有時則出現在習題中。

類似于這樣的經典題型，在小學數學習題教學中是很常見的。

“小數的意義”中的習題：一個兩位小數，保留一位小數后是2.6。這個兩位小數最大是（? ?），最小是（? ?）。

“分數的意義”中的習題：把一根5米長的繩子平均分成9段，每段長（? ?）米，每段占全長的（? ?）。

“圓的面積”中的習題：一塊草地上有一根木樁，上面用一根4米長的繩子拴著一只羊。這只羊最多能吃到草的面積是多少平方米？

上面三道習題，都是相對應知識習題中的經典題型，甚至像“小數的意義”和“分數的意義”中的習題，已經成為這些知識習題教學中的易錯題型。因此，像這樣的經典題型，如果在習題教學時沒有讓學生見識過，估計沒有一位教師心里是踏實的，因為這不僅關系到學生對相對應知識的理解和掌握，還關系學生的檢測成績。

由此可見，小學數學習題教學具有拓展學生對習題題型見識的功能。當然，這種見識不是僅僅見過這樣的習題，更是理解和掌握這些習題的解題策略。

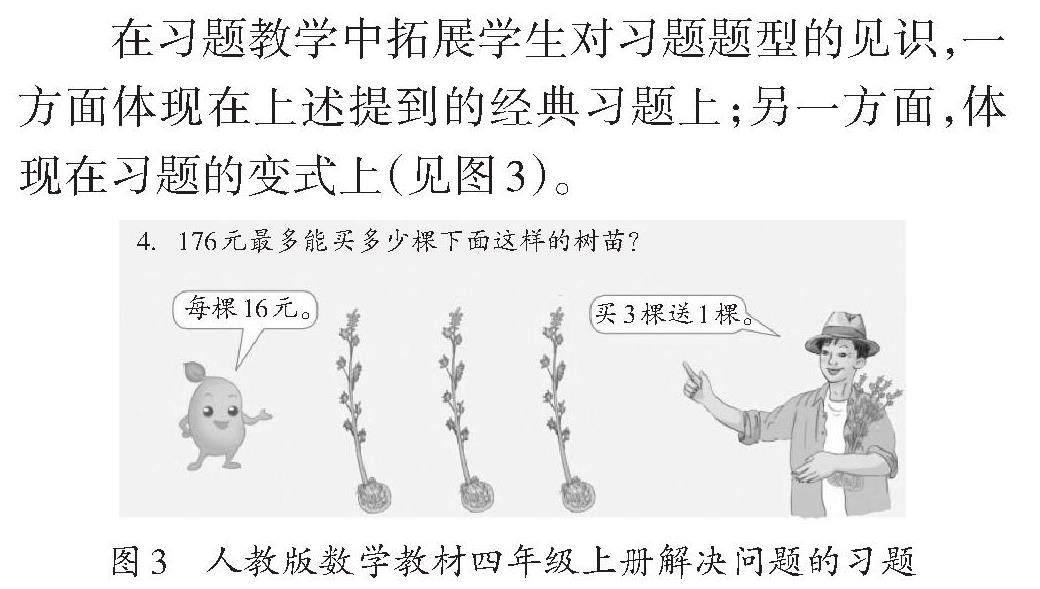
在習題教學中拓展學生對習題題型的見識，一方面體現在上述提到的經典習題上；另一方面，體現在習題的變式上（見圖3）。

[4.? ?176元最多能買多少棵下面這樣的樹苗？ ][每棵16元。][買3棵送1棵。]

圖3 人教版數學教材四年級上冊解決問題的習題

這是人教版數學教材四年級上冊“除數是兩位數的除法”單元“整理與復習”中的一道習題，其特點是首次出現了“買3棵送1棵”這樣購物問題中經典的“買幾送幾”的信息。因此，對于使用人教版數學教材的學生而言，面對這道習題是一種新的題型見識。教學中，通過直觀演示、圖示表征等方式，學生能較好地理解其中“買3棵送1棵”的意思，進而理解這道習題的解答方法。

但是，這道習題的教學到此還遠沒有結束。請看圖4，在與這節課配套的本地《課堂作業本》（浙江教育出版社，浙江省廳教研室組織編寫）中連續出現了這道習題的兩次變式。

[（4）商店舉行飲料促銷活動，下面是活動公告牌。媽媽付了120元錢，可以買到多少瓶這樣的飲料？按這樣計算，每瓶單價比原來便宜了多少元？] [12元/瓶

買5瓶送1瓶]

變式一

[6.小王在活動期間買到了這樣的4盒巧克力，每盒的實際價格是多少元？相當于每盒降價多少元？

][原價：128元/盒

活動期間買3盒送1盒][巧克力]

變式二

圖4 《課堂作業本》中的兩道變式題

變式一：增加了一個比較單價的問題。

變式二：將原本告知“總價”的條件變成告知“數量”的條件，問題也隨之發生變化。

因此，在教學這道習題時，絕不能僅僅滿足于這道習題本身，而要著眼于這道習題可能存在的變式，進一步拓展學生對題型的見識。類似于這樣的情況在小學數學習題教學中很常見，我們不妨再來看其他的例子。

“分數的意義”經典習題：一根繩子，用去全長的[14]，還剩下[14]米。請問這根繩子是用去的多，還是剩下的多？

“分數的意義”經典習題變式：（1）一根繩子，用去全長的[12]，還剩下[12]米。請問這根繩子是用去的多，還是剩下的多？（2）兩根一樣長的繩子，一根用去全長的[14]，另一根用去[14]米。請問哪根繩子用去的多？

一位有經驗的教師，會在教學經典習題后，教學變式習題；一位新手教師，則可能不會教學變式習題。因此，不管是從學生對知識、習題的理解和掌握來看，還是從最后的學科檢測成績來看，幫助學生拓展題型見識往往成了新手教師在教學質量上敗給有經驗教師的重要原因。所以，學生數學學習的疑難點，一般不是表現在數學知識和技能本身，而是表現在運用數學知識和技能解答某一類型的習題上。有沒有讓學生見識過多樣的、特別是經典的習題，對學生的數學學習非常重要。

綜上所述，小學數學習題教學具有拓展學生數學認識和習題題型見識的重要功能。

［ 參 考 文 獻 ］

[1] 喬治·波利亞.怎樣解題：數學思維的新方法[M].上海：上海科技教育出版社，2007.

[2] 何月豐.“乘法分配律”應用例題、典型題型現狀分析與教學改進建議[J].小學數學教師，2023（10）：41-50.

（責編 杜 華）