如何借助尺規畫圖幫助學生理解平行四邊形的特征

黃建

教學中，教師可以借助尺規畫圖的方式，幫助學生更好地理解平行四邊形的特征。具體可以采用以下教學過程。

一、根據要求選擇線段，并在想象后進行實際操作

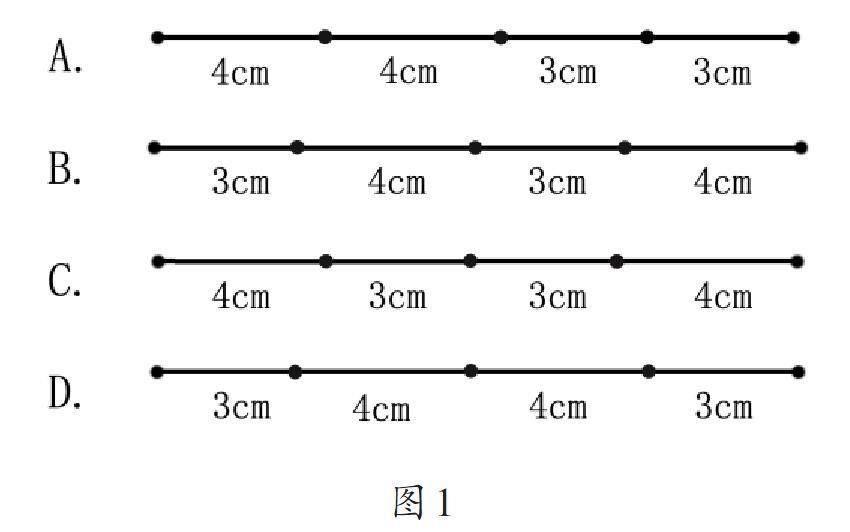
教師呈現圖1，引導學生根據給出的記號，判斷哪一條線段折疊后能夠形成一個平行四邊形。

學生先獨立思考，再小組交流。

接著，引導學生思考：為什么選B？在學生解釋原因的過程中，幫助他們理解平行四邊形中邊的特征，即平行四邊形的對邊長度相等。

教師提問：“請你們想象一下，這個平行四邊形具體可能會是什么形狀？”為了讓學生更直觀地理解可能的形狀，教師建議學生利用學具進行實際操作，先拼接線段，然后嘗試不同的拉伸方式。在操作活動中，學生發現：平行四邊形的邊長已經確定，但形狀并非唯一。

二、布置作圖任務，使用尺規工具繪制平行四邊形

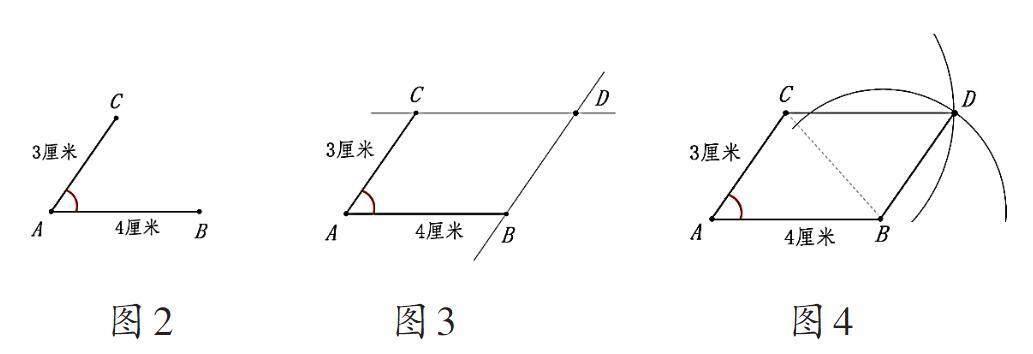
教師呈現圖2，展示平行四邊形的兩條相鄰邊，提問：“若角CAB的度數確定，通過圖中所示條件，能否確定這個平行四邊形的形狀是唯一的？”讓學生根據已知條件，利用兩把直尺和圓規，嘗試補全這個平行四邊形，并探究其形狀的唯一性。

學生獨立操作，用多種方法畫平行四邊形。

方法1：依據平行線的性質。通過點B，僅能繪制一條與AC平行的直線；同理，通過點C，也只能繪制一條與AB平行的直線。這兩條平行線的交點即為頂點D，如圖3所示。

方法2：運用圓規作圖。首先以點C為圓心，繪制一個半徑為4厘米的圓；然后以點B為圓心，繪制一個半徑為3厘米的圓。兩圓的交點即為所求頂點D，如圖4所示。

引導學生思考：為何兩圓的交點即為頂點D？幫助他們理解：頂點D至點B的距離固定為3厘米，頂點D至點C的距離固定為4厘米。當兩組對邊長度分別相等時，即可構成一個平行四邊形。兩圓的交點滿足這一條件，故為所求頂點D。

對比這兩種方法，它們的共同點即都在尋找交點。第一種方法尋找的是平行線的交點，其依據是平行四邊形的對邊分別平行；第二種方法尋找的是圓軌跡的交點，其依據是平行四邊形的對邊長度相等。因此，當平行四邊形兩條鄰邊的長度及其夾角確定后，其形狀便已固定下來。

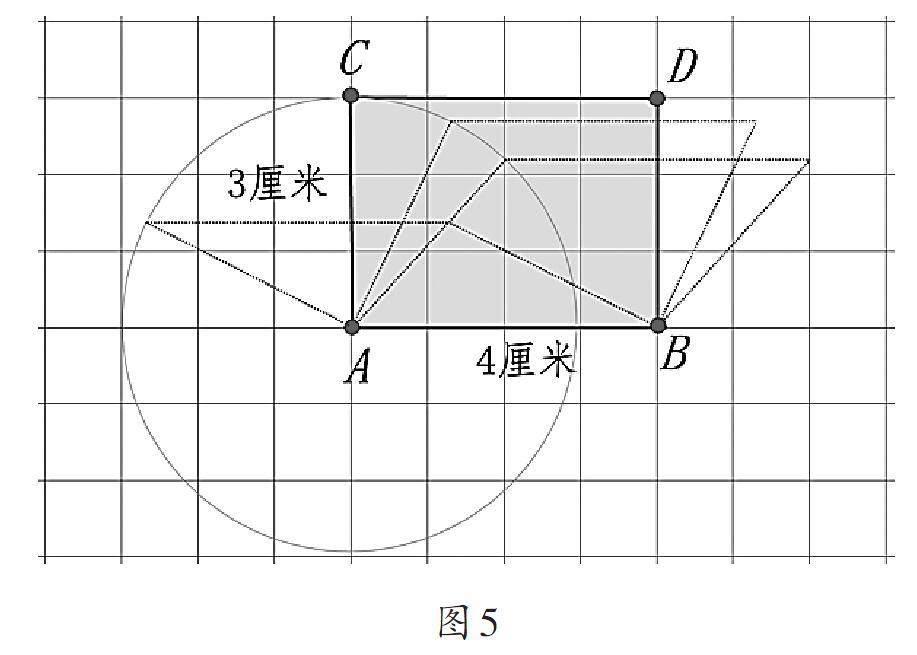
在圖4的基礎上，教師利用課件動態演示平行四邊形兩條鄰邊確定但其夾角不確定的情況。在觀察過程中，學生發現：平行四邊形的周長始終保持不變，但其面積卻會發生變化（如圖5）。當AC垂直于AB時（即成長方形），平行四邊形的高達到最大值，從而面積也達到最大值。

上述教學過程，讓學生在實物操作活動中，體會平行四邊形的不穩定性。同時，通過尺規作圖與想象，加深學生對平行四邊形特征的理解。

（浙江省杭州市勝利實驗學校）