信息科技課程中計算思維多層進階式目標體系設計

馮友梅 王昕怡 溫佳 王壯偉 顏士剛

基金項目：全國教育科學規劃2022年度教育部重點項目“本土計算思維描述框架及評價體系設計研究”（項目編號：DCA220445）

[摘? ?要] 計算思維是重要的信息科技學科核心素養，但面向計算思維的結構化教學體系尚未形成。經分析，計算思維目標體系的缺失是其直接原因。鑒于此，文章以“知識與思維內在統一”為基本立場，將計算思維轉換為與其內在統一的知識結構——計算思維二維描述框架，并設計知識結構水平的判斷標準——知識結構九水平分類體系。在此基礎上，給出二者相結合的計算思維目標體系設計方案并結合實例詳解：首先，將計算思維二維描述框架中的要素逐層分解以保證各教學單位均有其聚焦的計算思維要素；而后，以知識結構九水平分類體系為依據，形成縱向上層層細化、橫向上計算思維（知識）結構水平不斷提升的計算思維多層進階式目標體系。該目標體系設計方案可結束信息科技課程內容教學與計算思維教學兩條線的尷尬局面，使計算思維在與課程內容融合統一的教學路徑中真正落地。

[關鍵詞] 信息科技課程； 計算思維； 目標體系； 多層進階式； 知識結構九水平分類體系

[中圖分類號] G434? ? ? ? ? ? [文獻標志碼] A

[作者簡介] 馮友梅（1983—），女，河北香河人。副教授，博士，主要從事信息技術課程與教學、思維可視化理論與實踐研究。E-mail：youmeifeng2008@163.com。王壯偉為通訊作者，E-mail：wzhw0511@163.com。

一、引? ?言

作為核心素養落地的重要抓手，大單元教學在基礎教育領域備受推崇。其核心要義為，通過將作為“獨木”的課匯聚為作為“林”的單元，實現集中力量培養核心素養的教育目標。信息科技學科亦踐行此思路。作為信息科技學科聚焦的重要核心素養和學科立足之本[1]，計算思維的培養路徑當然也不例外。事實上，計算思維的有效培養，需要將課程作為整體集中發力。所謂集中發力，即要求在將課程匯聚為單元之后，各單元也要形成以計算思維發展脈絡為內在線索的、環環相扣的單元群。然而，截至目前，此種意義上的單元群尚未形成。換言之，在既有的所謂單元群（如各版本高中信息技術教材中呈現的單元群）中，很難找到計算思維的清晰進階脈絡，單元之間并未形成面向計算思維的合力。如此，從計算思維培養的角度看，單元便淪為新的“獨木”，學科依然未解決“獨木不成林”的痼疾。事實上，如何使計算思維培養系統化、結構化，亦是廣大信息科技教研員及一線教師倍感迷茫的問題。

鑒于此，本文深入分析信息科技課程中計算思維培養難成體系的原因——計算思維目標體系難以形成。在此基礎上，以“知識與思維內在統一”為基本立場，給出計算思維多層進階式目標體系的設計方案并結合實例詳解。借此為計算思維在信息科技學科穩妥落地提供真正可行且可被一線直接參照的思路和樣本。

二、面向計算思維的結構化教學體系

緣何難以形成

眾所周知，教學目標是教學實踐的重要線索和依據。從計算思維培養的角度來看，信息科技課程各教學單元間的“貌合神離”，正是緣于可將眾單元“黏合”成整體結構的計算思維目標體系的缺失。

對于計算思維單元目標設計，目前主要有以下三種方式：其一，在課程標準的“內容標準”中選取內容作為計算思維單元目標。如將計算思維單元目標確定為“描述人工智能的基本特征，利用開源軟硬件平臺設計搭建簡單智能系統”[2]。其二，將課程標準規定的計算思維學段目標（水平）作為單元目標。如將計算思維單元目標確定為“根據給定的任務進行需求分析，明確需要解決的關鍵問題”[3]。其三，將計算思維完整過程作為單元目標。如將計算思維單元目標確定為“通過經歷抽象、分解、算法設計、應用、評估、總結、遷移這一過程解決復雜問題”[4]。

以上三種計算思維單元目標設計方法中，第一種的問題最為突出，表現為單元目標與學段目標指向不一致，即計算思維單元目標與學段目標間無直接、明朗的關系，此為方向性錯誤。第二種及第三種目標設計方法雖錯不至此，但依然存在問題，即不同單元“共享”相同的計算思維目標。此問題在第三種目標設計方法中表現更甚：只要涉及計算思維目標，均用前文所示計算思維過程表示。結果是，看似每個單元均對計算思維的發展有所貢獻，但無法清晰說明具體貢獻是什么，即無法明確每個單元究竟在何種程度上促進了計算思維的發展。雖然以上三種目標設計方法存在的問題不同，但均導致了相同的結果：從計算思維培養的角度看，各單元之間僅是無清晰邏輯關聯的線性排列，與結構化教學體系相去甚遠。事實上，在第二種及第三種目標設計方法中，各單元之所以需“共享”同一計算思維目標，主要原因為目標的跨層使用，即用少量、抽象的學段甚至課程層面的計算思維目標指導大量、具體的單元層面的教學實踐。當然，很多研究者已經認識到目標跨層使用的不合理性，并嘗試將宏觀計算思維目標細化為多層關聯的目標體系，所做工作集中于對計算思維過程中內含的各要素或環節（“抽象”“算法設計”等）進行分解。例如，將“抽象”細化為“刪除”“過濾”“提取”“符號化”四個要素[5]等等。然而，無論采用何種思路，均無法分解出足夠多的計算思維“過程”要素，以支持為各個層面（包括單元層面）教學實踐提供明確計算思維目標的“金字塔結構”目標體系的形成。

計算思維目標體系的缺失，便意味著單元間無清晰的計算思維內在進階線索。結果便是，從計算思維培養的角度，信息科技課程各教學單元各自為政、形同散沙，難以形成面向計算思維的合力。進一步，單元無具體明確的計算思維目標，便無法有效開展計算思維單元評價，面向計算思維的“教—學—評”一體化也會落空。長此以往，計算思維很有可能淪落為“一個什么都能裝的筐”。

三、計算思維目標體系設計基礎及宏觀思路

除了計算思維所屬的學科核心素養，信息科技課程還有另一個核心范疇——學科大概念。其中，《普通高中信息技術課程標準》（2017年版）（以下簡稱“高中課標”）提煉出四個學科大概念，分別為“數據”“算法”“信息系統”和“信息社會”，《義務教育信息科技課程標準》（2022年版）（以下簡稱“義教課標”）亦提煉出六個學科大概念（也稱六大邏輯主線）。這些學科大概念是信息科技課程內容的基本框架。特別是高中階段，課程內容標準、教材各單元及單元內各節內容均以四個學科大概念逐層分解而成的目標體系為內在線索。因此，前文所言信息科技課程各教學單元間無清晰的內在關聯，是從計算思維培養的角度所得結論。從學科大概念的角度看，以課程標準及教材為依據的各教學單元則是線索清晰的整體結構。

然而，在當下基礎教育語境中，還無法以圍繞學科大概念形成的目標體系為中介或橋梁，形成計算思維目標體系。原因如下：無論是各方學者對計算思維的界定，還是課程標準對計算思維及其水平的描述，均從計算思維“過程”角度出發，如“能在真實情境中發現問題，提取問題基本特征，對問題進行抽象、分解、建模……[6]”等。從描述角度和方式看，計算思維與“數據”“算法”等更傾向于“內容”（知識）的學科大概念在發展過程及水平方面并無直接關聯。這與學界對思維“過程”與思維“內容”之關系的認識一脈相承。“知識（思維內容）是訓練思維（思維過程）的材料，是思維調動、利用的資源[7]”。此論斷在教育領域被普遍認同，其言下之意為，思維過程和思維內容間僅是調用與被調用的關系，二者在發展脈絡及水平方面并無內在實質關聯[8]。

于是，計算思維目標體系建構便遇到了一個難以逾越的瓶頸：一方面，從計算思維過程的角度，經多方努力，均無法形成多層關聯的目標體系；另一方面，因計算思維過程與內容無內在實質關聯，故無法以信息科技學科大概念目標體系為中介形成計算思維目標體系。困境就此產生。事實上，對于“思維過程與思維內容無內在實質關聯”這一論斷，教學實踐中已經出現與其相悖的案例。例如，“敏捷性”是衡量思維品質的重要標準[7]，已有教學實踐表明，增加知識（思維內容）節點間的關聯可顯著提升思維（思維過程）的敏捷性[9]。

源于對計算思維落地困境的擔憂，亦因大量反例給予我們的追問動力，自2016年起，經過層層追溯，筆者及團隊成員最終找到“思維過程與思維內容無內在實質關聯”這一論斷的直接來源——認知心理學關于學習核心機制的“信息加工”隱喻，并發現該隱喻的局限性[10]。在此基礎上，從皮亞杰發生認識論之哲學精髓處獲得啟發，得到關于思維過程與思維內容間關系的新認識：思維過程與思維內容是本質上不可分的統一整體，這一整體可表現為兩種狀態：靜態與動態。其中，靜態即知識，是陳述性知識與程序性知識復雜交織的知識結構；動態即思維，是以既有知識結構為基礎的知識結構再建構過程，其結果是新的知識結構的形成。此知識結構又是下一次思維運轉的基礎，如此螺旋上升，使得靜態的知識結構與動態的思維結構在發展過程與水平方面保持同步和統一[8]。

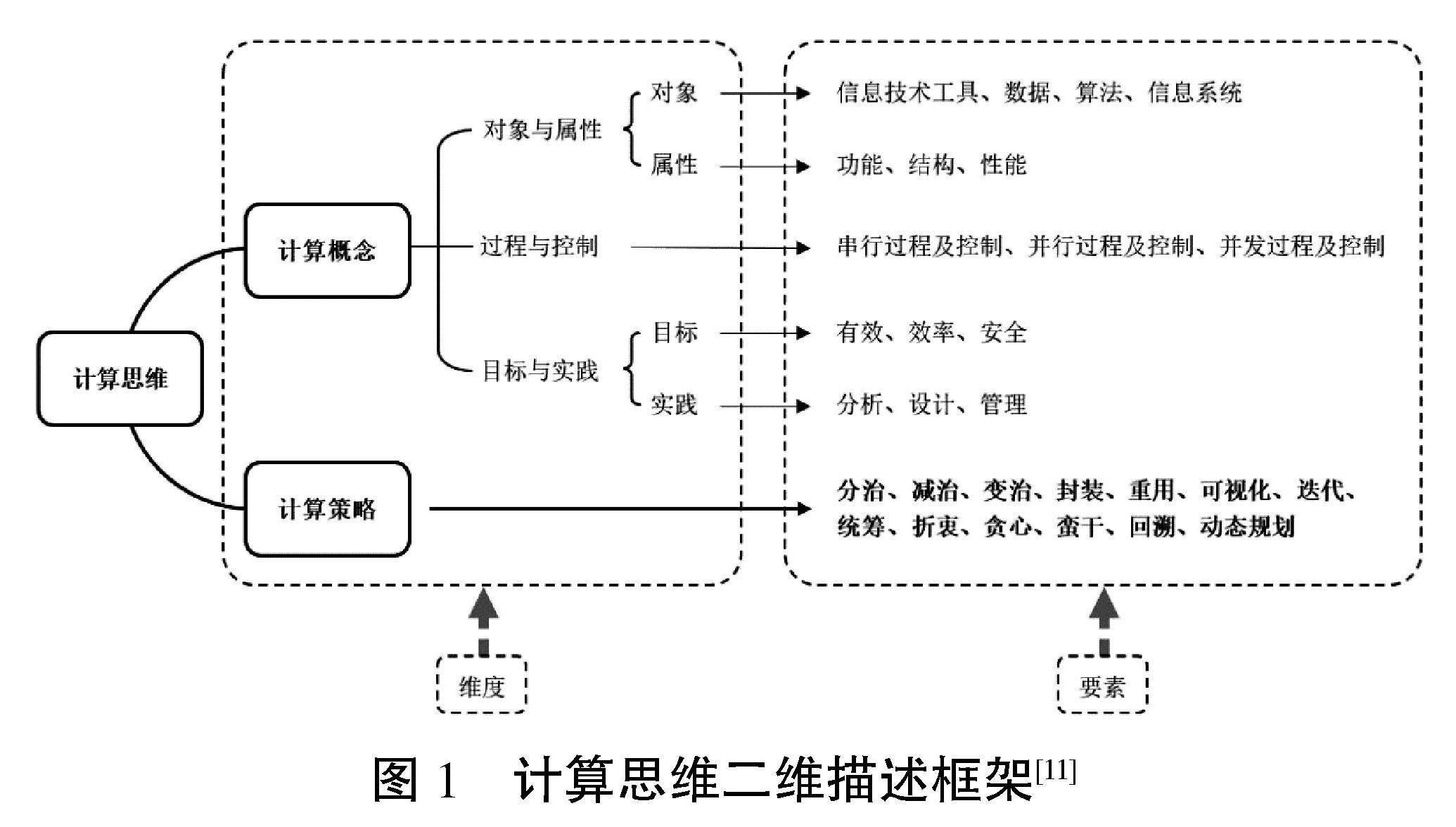
以“知識與思維內在統一”為基本立場，計算思維目標體系的建構困境便有了突破口：以與計算思維內在一致的學科大概念為中介，構建計算思維目標體系。以此為指導思想，以課程標準及教材為基礎，并從上游學科——計算機科學中汲取智慧，我們最終建構完成與計算思維動態過程內在一致的靜態大概念框架，包括計算概念與計算策略兩個維度，如圖1所示。其中，計算策略是核心。

圖1? ?計算思維二維描述框架[11]

此計算思維二維描述框架（以下簡稱“描述框架”）中所含要素皆為學科層面的大概念，亦是計算思維目標體系的建構基礎。基本建構思路為：將描述框架中的要素逐層分解，形成多層關聯的概念“金字塔結構”體系；在此基礎上，依據知識結構水平判斷標準，結合課程標準中關于計算思維學段目標、學段特征等的規定，便形成可為各層面教學提供明確計算思維目標的多層進階式目標體系。以此思路構建計算思維目標體系，亦可結束計算思維教學與課程內容（知識）教學兩條線的尷尬局面，使信息科技課程呈現出主線清晰的一體化邏輯脈絡和實踐路徑。

四、計算思維目標體系設計方案及例解

以計算思維目標體系設計基礎及宏觀思路為依據，本部分結合實例，給出具體詳細的計算思維目標體系設計方案。

（一）計算思維二維描述框架各要素的分解和細化

在真實的教學場域中，“課”是教學的基本單位。就計算思維的有效培養而言，不僅單元，單元上層的模塊、學段、課程，單元下層的課亦需要有明確的計算思維目標。因此，計算思維目標體系設計的第一步，便是對描述框架中的各要素進行分解，以保證每堂課、每單元等均有其聚焦的具體概念或大概念。以下分別闡釋計算概念和計算策略維度要素的具體分解思路。

對于計算概念維度的要素，主要有兩種分解思路：基于“整體—部分”關系的分解和基于“類屬”關系的分解。例如，從類屬關系的角度，“信息系統”可分解為“互聯網信息系統”和“物聯網信息系統”；從“整體—部分”關系的角度，“互聯網信息系統”可進一步分解為“計算機系統”和“通信網絡”……同理，計算概念維度的其他要素亦可依據此思路分解形成要素體系。

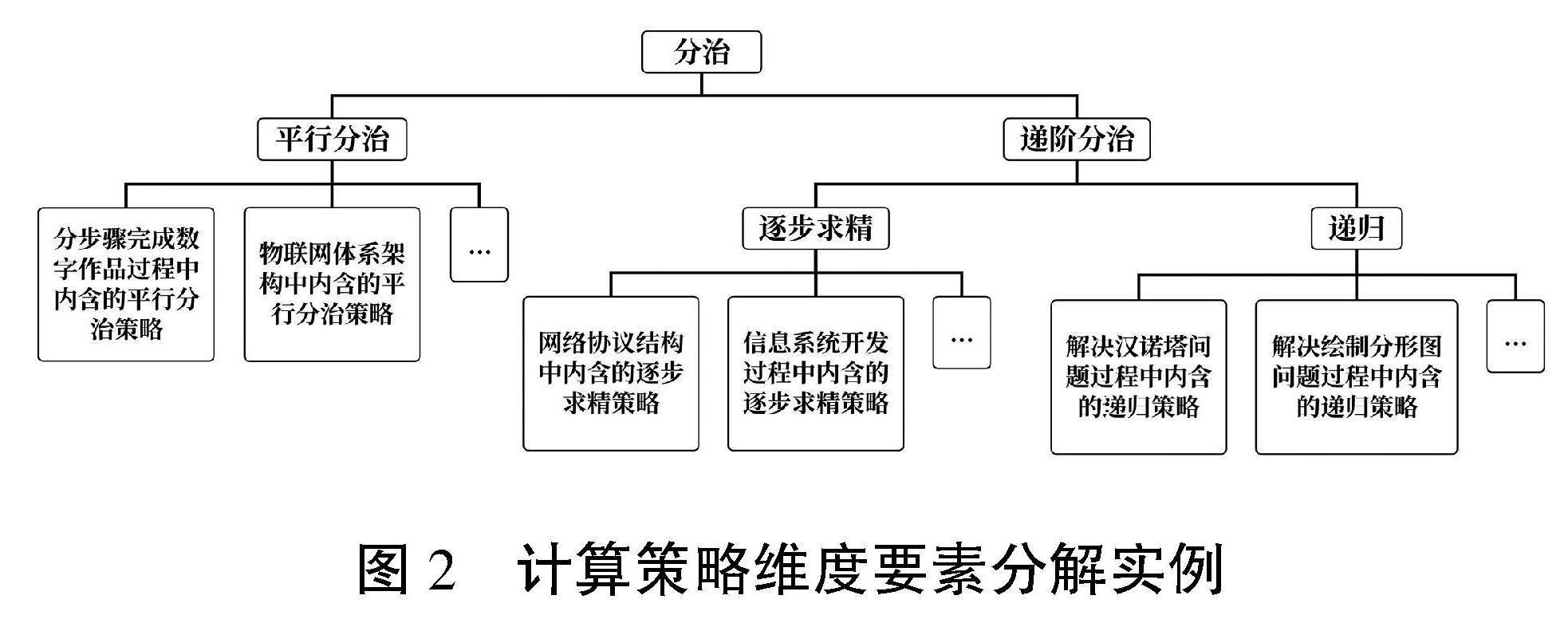
對于計算策略維度的要素，主要是基于類屬關系的分解。以“分治”策略為例，從子問題之間關系的角度，“分治”可分解為“平行分治”和“遞階分治”① ；“遞階分治”又可分解為“逐步求精”和“遞歸”兩種類型。從策略應用情境的角度，分解而成的以上要素還可進一步分解，具體如圖2所示。依據不同的分類標準，計算策略維度的其他要素均可分解成層層關聯的金字塔結構。

圖2? ?計算策略維度要素分解實例

（二）知識結構水平判斷標準的確定

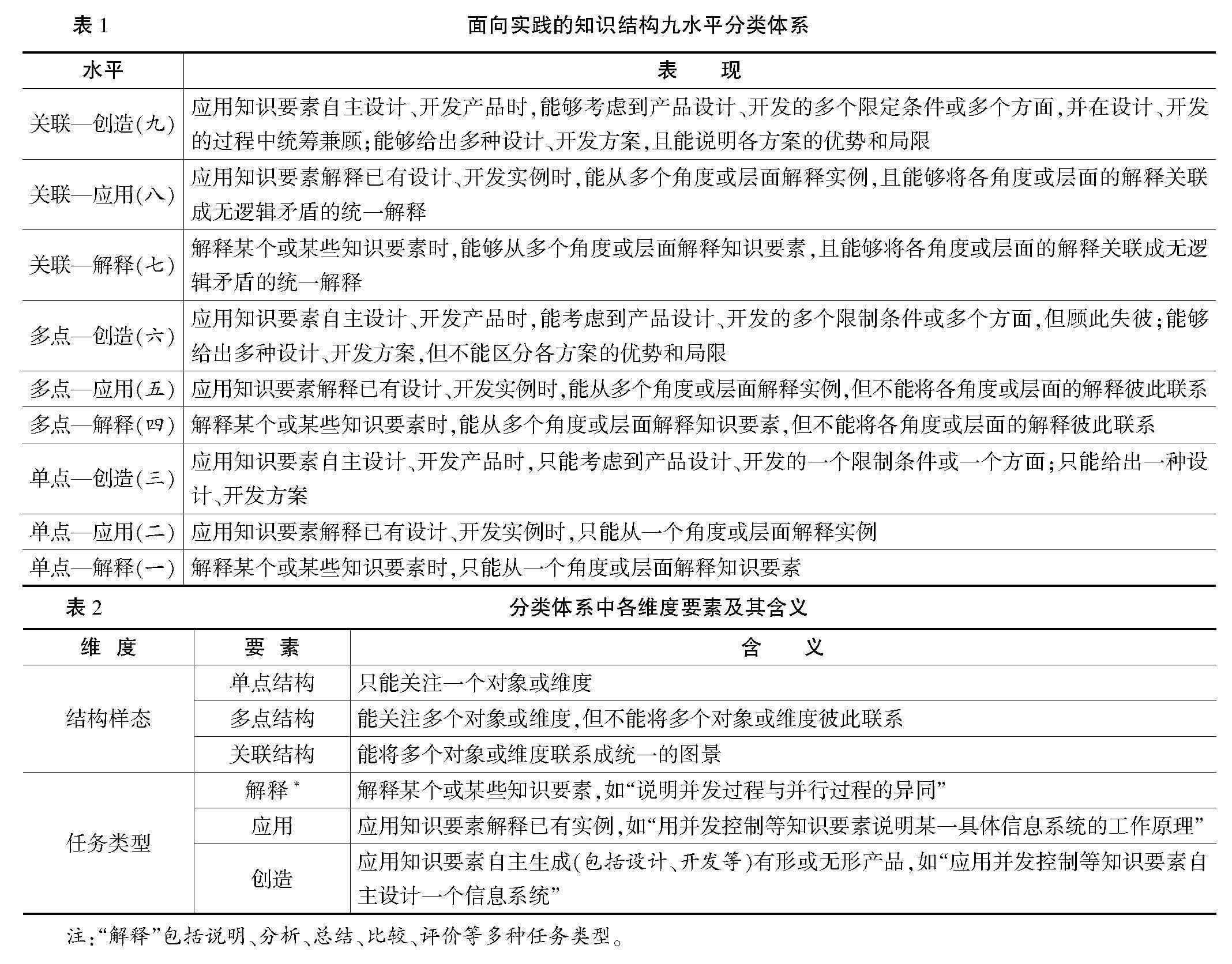
以發展計算思維為目的的知識教學，不再聚焦獨立的知識要素，而是以促進眾知識要素關聯形成高水平的知識結構為旨歸。換言之，雖然通過描述框架，將計算思維教學轉換為特定范圍內的知識教學，但這并非對傳統知識教學的簡單回歸，而是否定之否定——從知識點轉向知識結構。因此，需要一個以知識結構的復雜程度為水平劃分依據的目標分類體系，其與分解而成的知識要素體系相結合，形成計算思維目標體系。SOLO目標分類體系基本滿足此需求。該目標分類體系以思維結構（知識結構）的復雜程度為水平劃分標準，共包含五個水平，由低到高分別為“前結構”“單點結構”“多點結構”“關聯結構”及“拓展抽象結構”[12]。

然而，首先，“前結構”僅是一種理論樣態，當知識結構為教學目標時，“前結構”并不適合作為其水平判斷標準。其次，“拓展抽象結構”與“關聯結構”并無知識結構復雜程度的差異，區別僅在于是否發生結構遷移[13]。再次，雖然從理論上，SOLO目標分類體系中“單點結構”“多點結構”“關聯結構”三個層級可以較為精準地標識知識結構水平，但在完成教學目標所要求的學習或評價任務時，學生需要激活、關聯的知識要素往往多于教學目標顯性要求的知識要素及結構，即有部分知識結構處于內隱狀態。且對于知識結構顯性要求相同的教學目標，涉及的任務類型不同，完成其所需的處于內隱狀態的知識結構也存在差異，但一線實踐者往往難以辨別這些內隱狀態的差異。

鑒于以上，為了支持實踐領域合理地確定知識結構水平，本文借鑒薩蘭特（Salant）等人的思路[14]，將任務類型與SOLO目標分類體系中的“單點結構”“多點結構”“關聯結構”三個層級相結合，形成了面向實踐的知識結構九水平分類體系，見表1。相比“任務類型”，“結構樣態”在水平劃分時有較高優先級。分類體系中各維度要素及其含義見表2。該分類體系突破了薩蘭特（Salant）等人所創分類體系僅面向編程領域的局限，可應用于所有教學場域。

（三）計算思維多層進階式目標體系設計

以下筆者結合課程標準和教材，闡釋如何以計算思維知識要素體系及知識結構九水平分類體系為依據構建計算思維目標體系。

義務教育及高中課標規劃了前后相繼的若干模塊。故計算思維目標體系設計的一種易操作的思路為：將模塊作為單元群的設計單位，以其為中心，向下分解形成單元進階序列及課進階序列；向上匯聚為學段進階序列及課程整體，計算思維目標體系設計即是確定各層具體、明確的進階式目標序列，如圖3所示。以下從兩個方面詳解計算思維目標體系的設計方法：其一，各層目標中知識要素及知識結構水平的確定方法；其二，計算思維目標進階線索。

圖3? ?計算思維目標體系設計思路

1. 各層目標中知識要素及知識結構水平的確定方法

任何一個具體的計算思維目標均內含兩個基本成分：知識要素以及知識結構水平。各層目標的抽象程度不同，主要表現為各層目標所含知識要素的抽象程度不同。其中，課程層目標中的知識要素即為描述框架中的要素，其余各層目標中的知識要素均在分解而成的要素體系中遴選。在描述目標時，不必將目標中顯性要求的知識要素全部列出，只描述關鍵要素即可。對于知識結構水平的確定，因在目標統攝的范圍內會包含多種水平的具體知識結構（這在宏觀層面的目標中表現尤為明顯），故以其中最高知識結構水平作為目標水平① 。需要強調的是，在設計各層計算思維目標時，無論是知識要素的選擇抑或知識結構水平的確定，課程標準及教材均是重要依托，本文提供的計算思維要素體系及知識結構九水平分類體系則是對其進行以凸顯計算思維的發展脈絡為目的的二次創造的依據。

以計算思維課程層面的目標為例，依據本文給出的計算思維目標設計方法，對義教課標規定的計算思維課程目標進行二次創造，結果如下：“在真實問題情境下，通過數字工具支持的多種符形結合的表意及在線交流過程、數據分析與編碼過程、算法設計過程及簡單信息系統設計過程，初步理解過程與控制的基本原理，內化有效、效率、安全的目標意識以及可視化、分治、重用、迭代等計算策略，并將其遷移至其他學科及真實問題的求解中。”

從知識要素的角度，上述目標設計案例在保留義教課標所規定內容的基礎上，從中提煉補充了若干計算概念（如有效、效率）和計算策略（如可視化、分治）。因目標處于課程層面，故所補充的皆為描述框架中的知識要素，且僅描述了關鍵要素。從知識結構水平角度，義教課標包含“互聯網協議”這一教學內容，學生只有在教師的引導下（模擬）經歷協議的初步設計過程，才能真正理解②協議本身，并內化其內含的“分治”“封裝”等策略。設計互聯網協議的過程需要各層統籌兼顧，故為“關聯—創造”水平。即是說，義教課標要求學生本學科的知識結構（最高）水平為“關聯—創造”水平。

除知識要素的遴選范圍不同，其他各層計算思維目標設計思路與課程層目標基本一致，不再例解。

2. 計算思維目標進階線索

目標進階指目標的橫向進階，縱向上各目標間不存在進階關系。圖3中各層目標抽象程度不同，但進階線索一致，即知識要素增加及知識結構水平提升。具體分為三種情況：與目標進階脈絡中的前一個目標相比，目標中的知識要素增加，知識結構水平不變；知識要素未增加，知識結構水平提升；知識要素增加，知識結構水平亦提升。

進一步，知識結構的發展過程是三種結構的螺旋上升過程（如“單點結構→多點結構→關聯結構→多點結構→關聯結構……”）。因此，知識結構水平提升可以有兩種方式：第一種，同層提升，包含“單點結構→多點結構”“多點結構→關聯結構”“單點結構→關聯結構”三種情況；第二種，跨層提升，即螺旋上升后的提升，包含“關聯結構→（跨層）多點結構”“關聯結構→（跨層）關聯結構”兩種情況。再有，一般情況下，同一計算思維目標會與多個知識領域（目標進階脈絡）相關，進而表現出多個相對水平。

接下來以義務教育階段《互聯網應用與創新》模塊的計算思維目標體系設計（圖4）為例，詳解計算思維目標的進階線索。該設計實例中：將“單元二目標”置于互聯網知識領域。因該知識領域要求學生從外在應用及內在原理兩方面整體把握互聯網，“單元一目標”聚焦互聯網的外在應用，故其為“單點—創造”水平，包含的關鍵知識要素為“可視化”和“互聯網工具”。“單元二目標”則要求學生在單元一的基礎上，進一步（通過自主設計網絡協議的方式）理解互聯網的內在原理，初步形成對互聯網的整體認識。相比“單元一目標”，“單元二目標”增加了“網絡協議”“分治”等知識要素，目標水平進階為“關聯—創造”水平，屬于前文所述第三種目標進階方式。除了歸屬于“互聯網”知識領域，“單元二目標”還可置于“分治”知識領域進行考察。結合課程標準和教材，可得到“分治”知識領域一種可能的目標進階脈絡：“將數字設備的使用過程分解為若干步驟（平行分治）→將數字作品的設計與開發過程分解為若干步驟（平行分治）→用算法描述解決簡單問題的過程（平行分治）→將系統分解為若干子系統（平行分治）→初步（模擬）設計網絡協議（遞階分治）……”將“單元二目標”置于此脈絡中，其亦為“關聯—創造”①水平。此外，“單元二目標”還可置于“封裝”“統籌”“效率”等知識領域進行考察，從而在不同的進階脈絡中表現出相同或不同的目標水平。縱向角度，“單元二目標”與單元二內課層各目標間并不存在進階關系；橫向角度，單元二內課層各目標同樣可置于不同目標進階脈絡中考察，進而表現出多種相對目標水平。篇幅所限，不再贅述。

圖4? ?計算思維目標體系設計實例

綜上所述，計算思維目標進階脈絡錯綜復雜，并非僅同層相鄰目標間的簡單關聯。此是計算思維目標進階的應然狀態，同一計算思維目標亦因此表現出多種相對水平。鑒于此，在教學實踐中，教師不必執著于確定特定計算思維目標處于何種水平，而應將關注點放在促進知識要素間建立盡可能豐富的關聯上。這便要求教師在設計各層面目標時均有全局意識，如此才能真正引導、支持學生建構復雜關聯的、高水平的與計算思維內在一致的知識結構。這正是本文給出的知識結構九水平分類體系之于教學實踐的關鍵引導價值所在。

事實上，除了對計算思維目標設計的引導，知識結構九水平分類體系（任務類型維度）對于計算思維落地的另一關鍵要素——學習任務設計亦有重要的引導價值。受限于篇幅及本文主題，此處對學習任務設計僅作簡要闡釋（另文詳解），以期為實踐領域提供必要的方向性指導。依前文所述，在知識結構九水平分類體系的三種任務類型中，“創造”之所以水平最高，原因在于完成“創造”類任務需要學生在頭腦中建構知識要素間更多、更復雜的關聯，這正是教學過程的旨歸。例如，圖4中單元二便將“初步（模擬）設計網絡協議”這一“創造”類任務作為學習任務。通過完成此任務，學生不僅能夠深入理解互聯網數據傳輸的內部原理，而且可以通過（模擬）經歷這一“科學原理”的創造過程，內化蘊含其中的分治、統籌、封裝策略以及效率這一目標意識。如此才能充分發揮“科學原理”教學對于計算思維發展的潛在價值[15]。反之，如果將單元二的學習任務確定為“應用”類任務，如“探究（解釋）互聯網中數據傳輸的內部原理”，那么依托此學習任務，學生習得的僅是科學原理本身，根本無法領悟蘊含其中的對于計算思維發展而言至關重要的計算概念和計算策略[11]。綜上所述，在時間、資源等條件允許的情況下，應盡可能選擇“創造”類任務作為信息科技課程的學習任務，形成以“創造”類學習任務為主，“應用”類學習任務為輔的信息科技課程學習任務體系。

五、結? ?語

本文始于信息科技課程中計算思維培養難成體系這一實踐困境，并將困境原因歸結為計算思維目標體系的構建困境。在此基礎上，以“知識與思維內在統一”為基本立場，以計算思維二維描述框架及知識結構九水平分類體系為重要依據，給出信息科技課程中計算思維多層進階式目標體系設計具體方案。該方案可結束信息科技課程內容教學與計算思維教學兩條線的尷尬局面，使計算思維在與課程內容融合統一的教學路徑中真正落地。

在后續研究中，我們將重點做以下兩項工作：其一，在縱向上，以課程標準和教材為依托，系統梳理計算思維二維描述框架中各要素的進階脈絡，為教師從整體把握課程進而設計廣泛關聯的計算思維目標體系提供更充分的支持；其二，深入研究面向計算思維的學習任務及學習任務體系的設計方法，以支持計算思維目標體系有效達成。

計算思維對于學生未來發展的奠基作用毋庸置疑，但至今仍未有可落實于常規教學中的、成熟的計算思維培養體系。我們在為此努力，也期待更多研究及實踐者的加入！

[參考文獻]

[1] 馮友梅，王昕怡，劉曉蕊，張雪.計算思維不是什么：論計算思維的邊界及其何以成為信息技術學科的立足之本[J].電化教育研究，2023（1）：84-90.

[2] 中國教育技術協會信息技術教育專業委員會.全國信息技術優質課資源[DB/OL].（2022-09-22）[2023-07-26].http：//112.15.150.219：8028/.

[3] 中華人民共和國教育部.普通高中信息技術課程標準（2017年版）[S].北京：人民教育出版社，2018.

[4] 張翠紅.基于計算思維能力培養的單元教學設計[J].江蘇教育研究，2019（33）：66-71.

[5] 陳興冶，馬穎瑩.本土化計算思維評價指標體系的構建與探索——基于1410名高中生的樣本分析與驗證[J].遠程教育雜志，2020（5）：70-80.

[6] 中華人民共和國教育部.義務教育信息科技課程標準（2022年版）[S].北京：北京師范大學出版社，2022.

[7] 林崇德.我的心理學觀——聚焦思維結構的智力理論[M].北京：商務印書館，2008.

[8] 馮友梅，顏士剛，李藝.從知識到素養：聚焦知識的整體人培養何以可能[J].電化教育研究，2021（2）：5-10.

[9] 胡衛平.胡衛平.關注方法和品質，有效培養學生思維能力[R/OL].（2022-01-27）[2023-07-26].https：//mp.weixin.qq.com/s/AskLJwy8tWcMKV34frjN2A.

[10] 馮友梅.支持素養教育的教育目標描述模型設計研究[D].南京：南京師范大學，2019.

[11] 馮友梅，王珊，王昕怡，周彤彤.支持我國信息技術課程評價體系構建的計算思維描述框架設計[J].電化教育研究，2022（6）：115-121.

[12] BIGGS J B，COLLIS K F. Evaluating the quality of learning—the SOLO taxonomy[M]. New York：Academic Press，1982：85.

[13] 王較過，趙歡苗.SOLO分類理論在物理教學設計中的應用[J].當代教師教育，2012（1）：57-62.

[14] MEERBAUM-SALANT O， ARMONI M， BEN-ARI MM. Learning computer science concepts with scratch[J]. Computer science education， 2013（3）：239-264.

[15] 馮友梅，王昕怡，溫佳，馬小蘭，顏士剛.信息科技課程中“科學原理”的核心教學方法：歸于算法，始于算理[J].現代教育技術，2023（7）：35-43.

Designing A Multi-level Progressive Target System for Computational Thinking in Information Technology Curriculum

FENG Youmei1，? WANG Xinyi1，? ?WEN Jia1，? WANG Zhuangwei2，? YAN Shigang1

（1.Faculty of Education， Tianjin Normal University， Tianjin 300387;

2.Hebei Provincial Teacher Qualification Accreditation Service Center， Shijiazhuang Hebei 050051）

[Abstract] Computational thinking is an important core competence in information technology discipline， but a structured teaching system for computational thinking has not yet been formed. Through analysis， it is found that the lack of an target system for computational thinking is the direct cause. In view of this， this paper takes "the internal unity of knowledge and thinking" as the basic standpoint， converts computational thinking into a knowledge structure， a two-dimensional descriptive framework of computational thinking， and designs the judgment standard of knowledge structure， a nine-level classification system of knowledge structure. On this basis， the design scheme of computational thinking target system combining the two is given and explained in detail with examples. Firstly， the elements in the two-dimensional descriptive framework of computational thinking are decomposed layer by layer to ensure that each teaching unit has its own focus on the elements of computational thinking. Then， based on the nine-level classification system of knowledge structure， a multi-level progressive target system of computational thinking is formed， which is vertically refined layer by layer and is horizontally upgraded in the level of computational thinking （knowledge） structure. This design scheme can end the embarrassing situation between content teaching and computational thinking in information technology curriculum， so that computational thinking can be truly realized in the teaching approach that is integrated and unified with the content of the course.

[Keywords]? Information Technology Curriculum； Computational Thinking； Target System； Multi-level Progressive System; Nine-level Classification System of Knowledge Structure