寬轉子極無軸承開關磁阻電機徑向力模型全周期拓展

摘 要：

針對單繞組寬轉子極無軸承開關磁阻電機在定轉子極非完全交疊區間的徑向懸浮力模型空白、已有定轉子極完全交疊區間徑向懸浮力模型推導過程復雜且計算量大的不足，首先通過磁場有限元分析，分別確定了該電機在定轉子非完全交疊區間和完全交疊區間的電磁場幾何分布，計算了氣隙磁密，再根據麥克斯韋應力法分別推導了這2個區間的徑向力表達式，從而建立該電機在一個完整周期范圍內的徑向力數學模型，并通過與三維有限元計算結果的對比驗證該模型的準確性。相比于利用等效磁路圖推導徑向力模型而言，該建模過程更簡便，計算量也更小。全周期徑向力模型的建立，不僅能為電機本體和控制器設計提供理論參考，還有助于提高該電機控制策略設計的靈活性，也可以提高與傳統單繞組無軸承電機控制器的通用性。

關鍵詞：無軸承開關磁阻電機；單繞組；寬轉子；徑向力；全周期；麥克斯韋應力

DOI：10.15938/j.emc.2024.02.018

中圖分類號：TM352

文獻標志碼：A

文章編號：1007-449X（2024）02-0182-09

收稿日期： 2022-08-04

基金項目：江蘇省重點研發計劃（BE2021094）；國家自然科學基金（51977103，51877101）；南京工程學院校級科研基金（YKJ202208）

作者簡介：周云紅（1982—），女，博士，教授，研究方向為磁懸浮傳動技術、磁阻電機及其驅動技術、智能配用電技術等；

王 東（1994—），男，碩士研究生，研究方向為無軸承開關磁阻電機設計與應用；

黃 飛（1998—），男，碩士研究生，研究方向為無軸承開關磁阻電機優化控制；

孫玉坤（1958—），男，博士研究生，教授，研究方向為城軌交通再生制動控制技術、新能源汽車高效能動力電池與能量管理等；

譚正一（1998—），男，碩士研究生，研究方向為磁阻電機分析設計。

通信作者：周云紅

Full-period extension of radial force model for bearingless switched reluctance motor with wide rotor

ZHOU Yunhong， WANG Dong， HUANG Fei， SUN Yukun， TAN Zhengyi

（School of Power Engineering， Nanjing Institute of Technology， Nanjing 210000， China）

Abstract：

For single winding bearingless switched reluctance motor with wide rotor （BSRMWR）， there is still no radial suspension force model when rotor poles are not completely overlapped with stator poles. The existing radial suspension force model even has the shortcomings of complex derivation process and large amount of calculation when rotor poles are completely overlapped with stator poles. Therefore， the geometric distribution of the electromagnetic field of single winding BSRMWR both in the incompletely overlapping region and in the completely overlapping region of stator poles and rotor poles were analyzed with the magnetic field finite element analysis respectively， and the expressions of air gap magnetic density were obtained. Then the radial force expressions in these two regions were derived respectively according to the Maxwell stress method， and the mathematical models of the radial force of single winding BSRMWR in a full period were established. Finally， the accuracy of the deduced models was verified by comparing with the three-dimensional finite element calculation results. Compared with the equivalent magnetic circuit diagram method， the presented modeling process is simpler and less computational. The establishment of full-period radial force models can not only provide theoretical reference for the design of single winding BSRMWR and its controller， but also can help to improve the flexibility of the control strategy design and the versatility with the traditional single winding bearingless switched reluctance motor controller.

Keywords：bearingless switched reluctance motor; single winding; wide rotor; radial force; full period; Maxwell stress

0 引 言

無軸承開關磁阻電機（bearingless switched reluctance motor，BSRM）不僅具有普通開關磁阻電機（switched reluctance motor，SRM）的結構緊湊、容錯性高，魯棒性和可靠性強等優點［1］，還具備磁軸承電機摩擦小，轉速高的優點，因而在航空高速和超高速起動發電機等領域具有獨特優勢［2］。自20世紀90年代以來，關于BSRM的研究就得到廣泛關注，這也使得SRM的無軸承技術逐漸成為近年來的研究熱點［3］。

按繞組套數來分，目前對于BSRM的研究主要包括雙繞組無軸承開關磁阻電機（double winding bearingless switched reluctance motor，DWBSRM）和單繞組無軸承開關磁阻電機（single winding bearingless switched reluctance motor，SWBSRM）。最早研究的為DWBSRM，通過在開關磁阻電機的基礎上額外增加了一套懸浮繞組，由主繞組與懸浮繞組共同作用產生使轉子懸浮的徑向力，其中主繞組負責提供徑向力所需的偏置磁場，而懸浮繞組產生徑向力所需的控制磁場［4］。為了減少電機制造成本，進一步提高與開關磁阻電機的通用性，SWBSRM被提出，其每個定子極上僅纏繞一套線圈，通過線圈電流的不對稱控制，同時產生轉子旋轉所需的電磁轉矩以及懸浮所需的徑向力［5］。由于BSRM是一個非線性、強耦合的復雜系統，利用常規的SRM鐵心結構在實踐中較難實現轉矩和懸浮力的解耦控制，因此BSRM的新型拓撲結構也是一個重要研究方向。對于SWBSRM，文獻［6-7］提出一種8/10極的不等寬定子極結構，以寬極和窄極分別作為懸浮極和轉矩極，分別負責產生電磁轉矩和徑向懸浮力。文獻［8］在文獻［6-7］所述電機結構的基礎上提出了12/14極混合定子極結構，使電機磁路變短，解耦性加強，還降低了電機的鐵耗。文獻［9］提出一種6/4極結構的錐形SWBSRM，因定、轉子極面存在傾斜角，故轉子受到的垂直于轉子極表面的橫截面作用力可以分解為實現徑向懸浮的徑向力和驅動電機連續旋轉的切向力。文獻［10］提出一種12/8極寬轉子極結構的SWBSRM，采用雙向導通模式，實現電機轉矩以及懸浮力的解耦。

BSRM的本體設計和控制策略的研究都需要以準確的數學模型作為理論依據，徑向力解析模型的推導是BSRM懸浮控制策略的基礎。文獻［11］針對共懸浮繞組式無軸承開關磁阻電機，利用麥克斯韋應力法推導了考慮磁飽和的徑向力模型。文獻［12］在等效磁路法和虛位移法的基礎上，通過引入輔助函數以及運用查表法建立了對8/6極SWBSRM的徑向力和轉矩數學模型。文獻［13］推導了考慮轉子偏心的SWBSRM徑向力模型。文獻［14］根據磁導分段思想應用虛位移法構建了12/8極SWBSRM在一個周期內的全角度數學模型。文獻［15］通過構建等效磁路圖的方法建立了12/8極單繞組寬轉子齒無軸承開關磁阻電機（bearingless switched reluctance motor with wide rotor，BSRMWR）在定轉子極完全交疊區間內的徑向懸浮力模型。

本文在文獻［15］的基礎上，以單繞組BSRMWR為研究對象，基于麥克斯韋應力法推導一個完整周期內的徑向力數學模型，以彌補該電機在定轉子極非完全交疊區間徑向力模型的空白。相較于利用等效磁路圖推導徑向力模型的方法，本文的建模過程更簡便，計算量也更小。全周期徑向力模型的建立，可以為電機本體的分析設計提供更全面的依據，也有助于提高該電機控制策略設計的靈活性以及與傳統SWBSRM控制器的通用性。

1 單繞組BSRMWR的懸浮原理

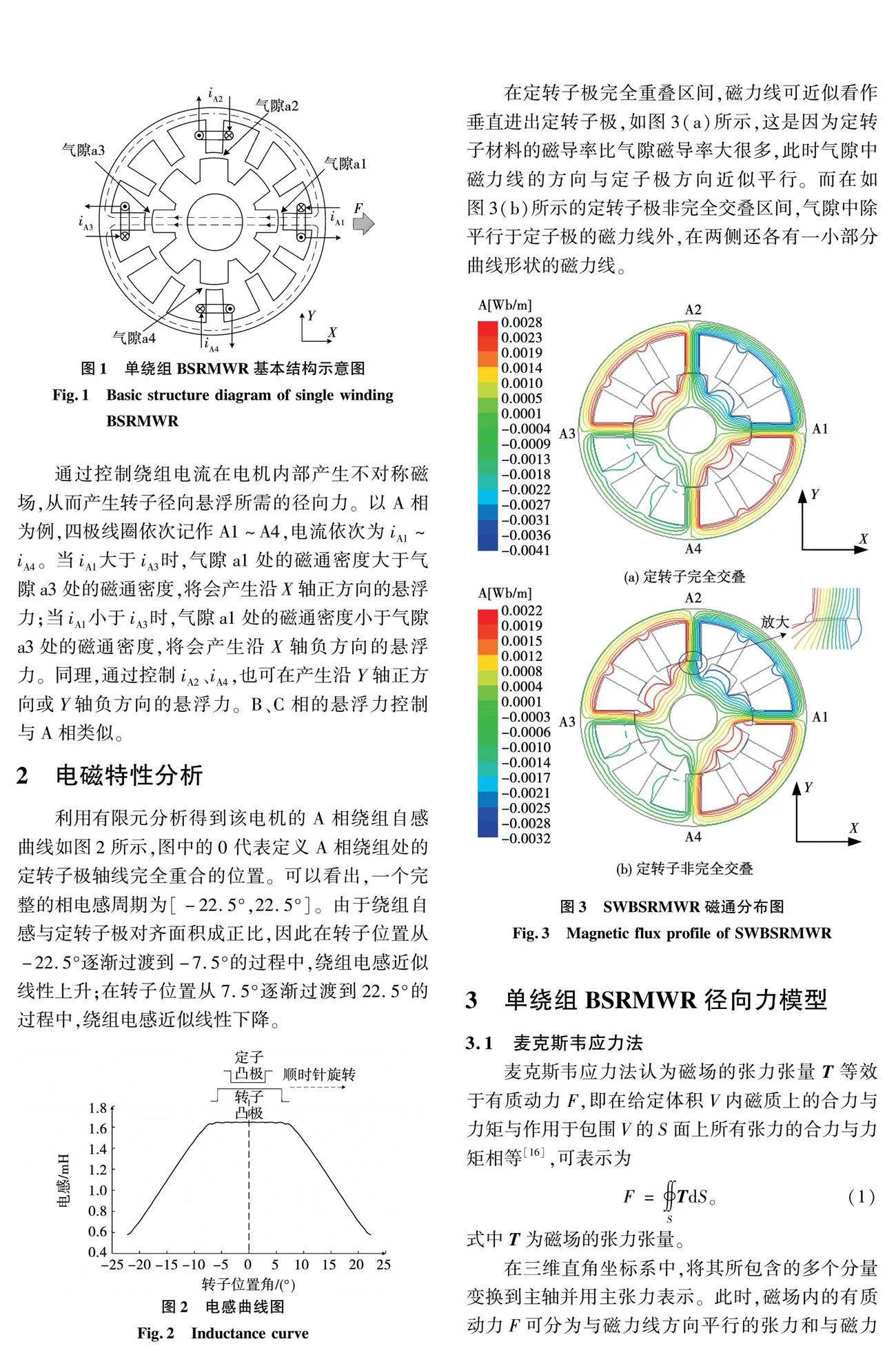
單繞組BSRMWR的基本結構如圖1所示，以12/8雙凸極結構為例，12個定子極依次相隔30°，8個轉子極等距離排列，定、轉子極弧角分別為15°和30°。每個定子極上均繞有N匝繞組，徑向垂直相對的四極構成一相但彼此并不串接，磁通呈NSNS分布。12極繞組共分為A、B、C三相，電流均可以獨立控制（圖中省略了B、C相繞組）。

通過控制繞組電流在電機內部產生不對稱磁場，從而產生轉子徑向懸浮所需的徑向力。以A相為例，四極線圈依次記作A1～A4，電流依次為iA1～iA4。當iA1大于iA3時，氣隙a1處的磁通密度大于氣隙a3處的磁通密度，將會產生沿X軸正方向的懸浮力；當iA1小于iA3時，氣隙a1處的磁通密度小于氣隙a3處的磁通密度，將會產生沿X軸負方向的懸浮力。同理，通過控制iA2、iA4，也可在產生沿Y軸正方向或Y軸負方向的懸浮力。B、C相的懸浮力控制與A相類似。

2 電磁特性分析

利用有限元分析得到該電機的A相繞組自感曲線如圖2所示，圖中的0代表定義A相繞組處的定轉子極軸線完全重合的位置。可以看出，一個完整的相電感周期為［-22.5°，22.5°］。由于繞組自感與定轉子極對齊面積成正比，因此在轉子位置從-22.5°逐漸過渡到-7.5°的過程中，繞組電感近似線性上升；在轉子位置從7.5°逐漸過渡到22.5°的過程中，繞組電感近似線性下降。

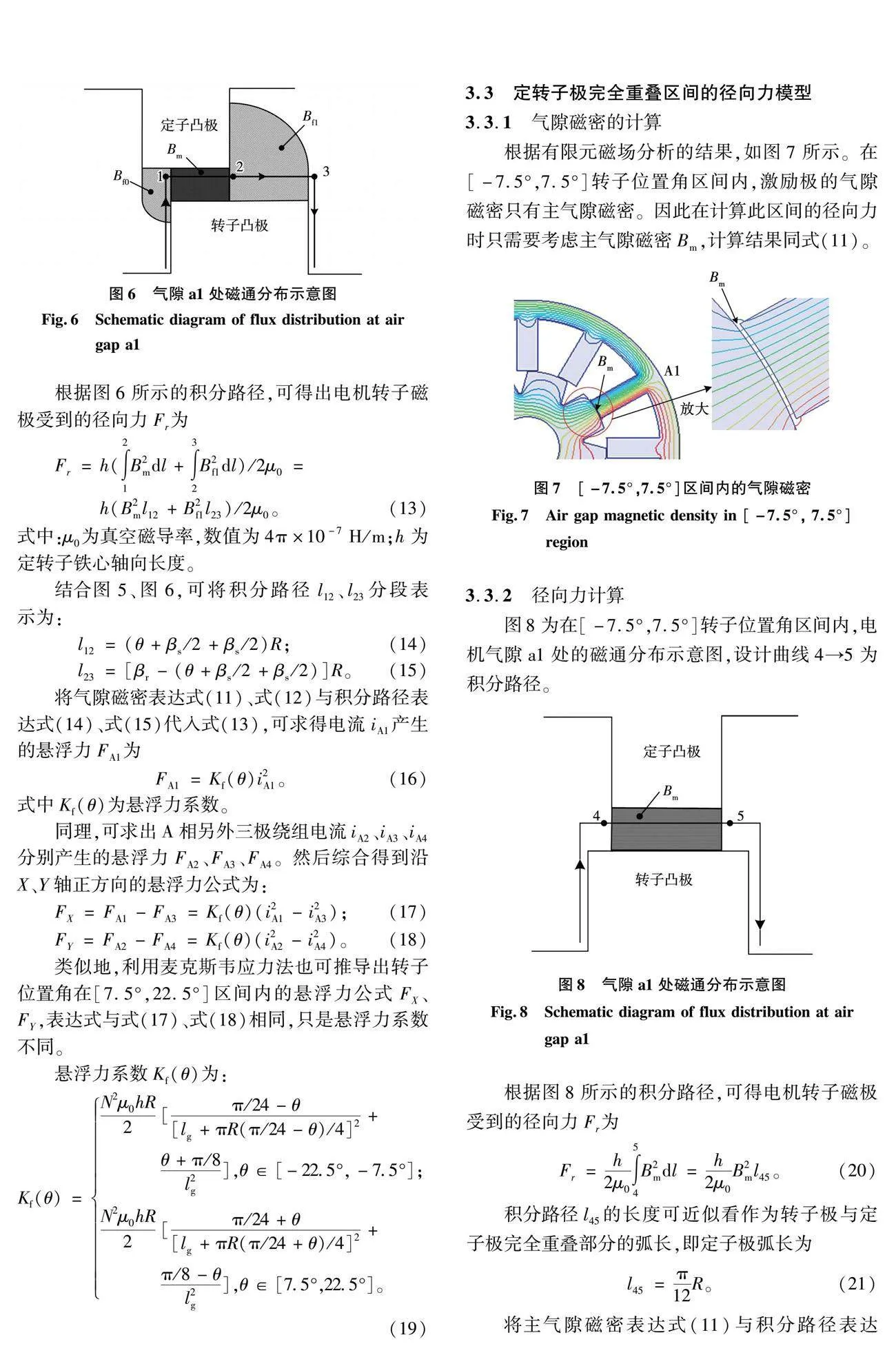
在定轉子極完全重疊區間，磁力線可近似看作垂直進出定轉子極，如圖3（a）所示，這是因為定轉子材料的磁導率比氣隙磁導率大很多，此時氣隙中磁力線的方向與定子極方向近似平行。而在如圖3（b）所示的定轉子極非完全交疊區間，氣隙中除平行于定子極的磁力線外，在兩側還各有一小部分曲線形狀的磁力線。

4 徑向力模型有限元驗證

以上分別推導了單繞組BSRMWR在定轉子極完全交疊以及非完全交疊區間的徑向力模型。為驗證所建立數學模型的準確性，本節利用有限元分析軟件Maxwell 3D建立三維樣機，主要參數見表1。

4.1 磁密驗證

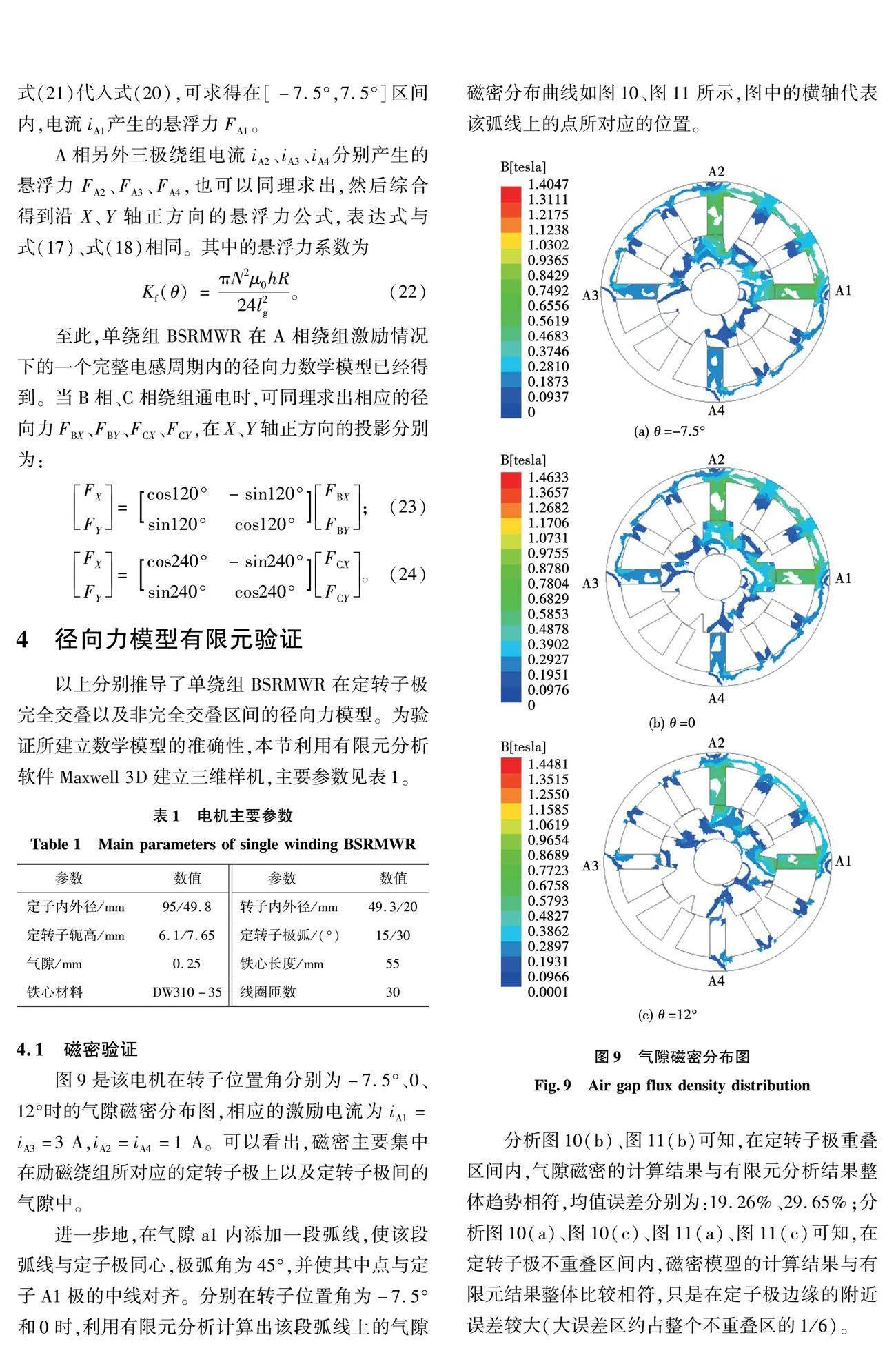
圖9是該電機在轉子位置角分別為-7.5°、0、12°時的氣隙磁密分布圖，相應的激勵電流為iA1=iA3=3 A，iA2=iA4=1 A。可以看出，磁密主要集中在勵磁繞組所對應的定轉子極上以及定轉子極間的氣隙中。

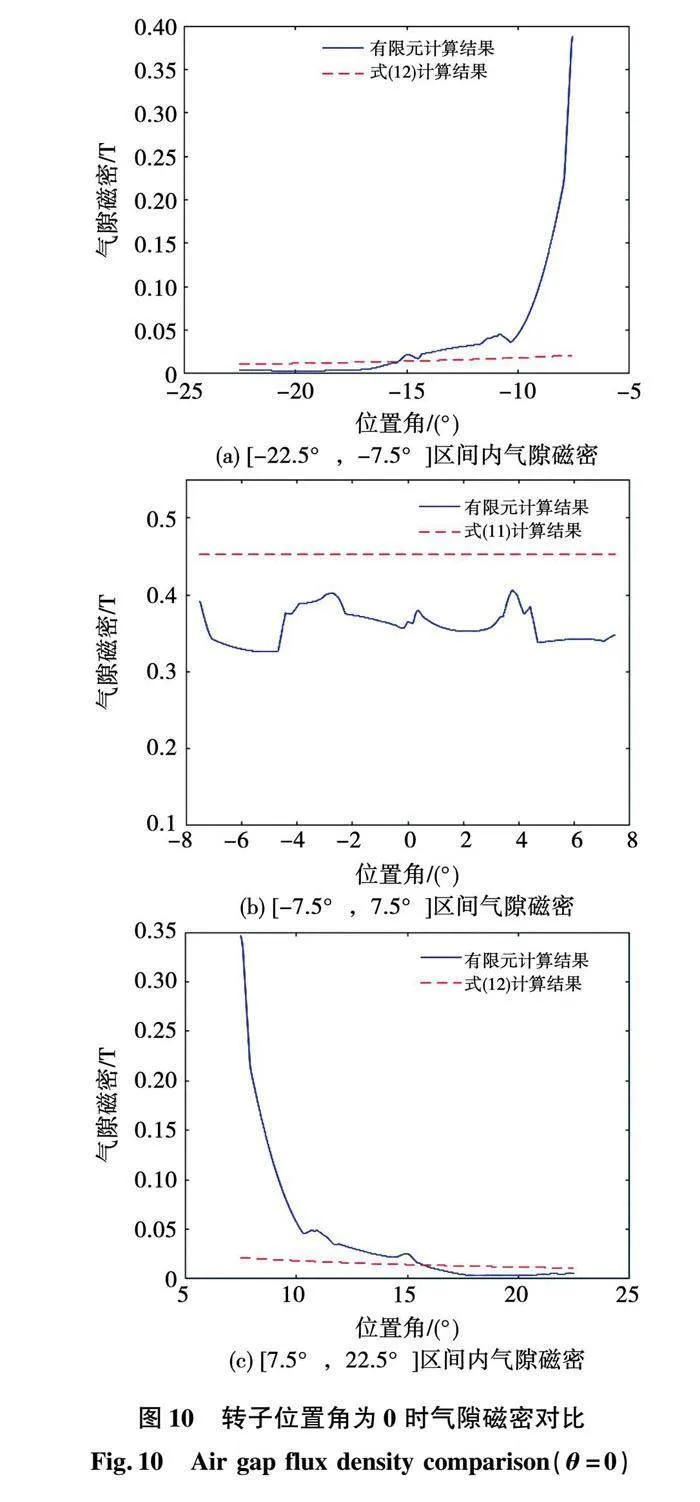
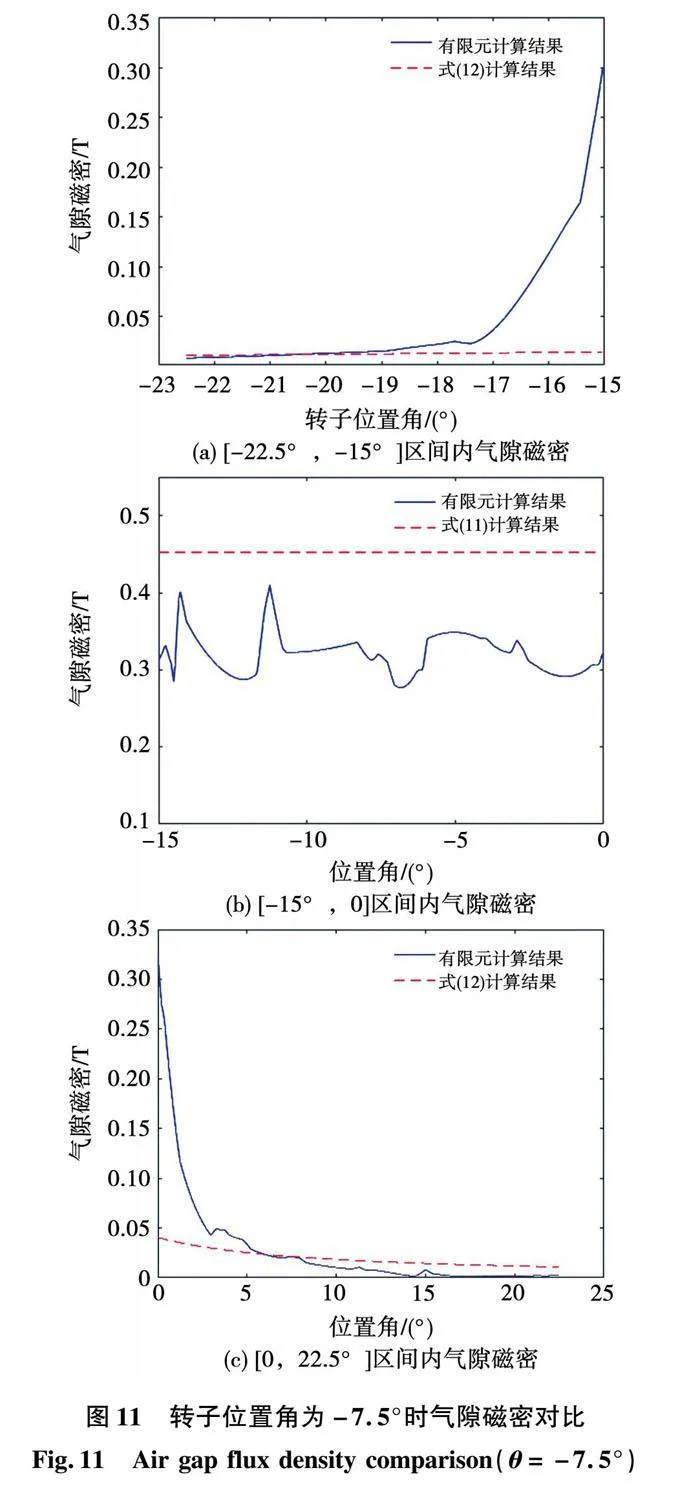
進一步地，在氣隙a1內添加一段弧線，使該段弧線與定子極同心，極弧角為45°，并使其中點與定子A1極的中線對齊。分別在轉子位置角為-7.5°和0時，利用有限元分析計算出該段弧線上的氣隙磁密分布曲線如圖10、圖11所示，圖中的橫軸代表該弧線上的點所對應的位置。

分析圖10（b）、圖11（b）可知，在定轉子極重疊區間內，氣隙磁密的計算結果與有限元分析結果整體趨勢相符，均值誤差分別為：19.26%、29.65%；分析圖10（a）、圖10（c）、圖11（a）、圖11（c）可知，在定轉子極不重疊區間內，磁密模型的計算結果與有限元結果整體比較相符，只是在定子極邊緣的附近誤差較大（大誤差區約占整個不重疊區的1/6）。

4.2 徑向力驗證

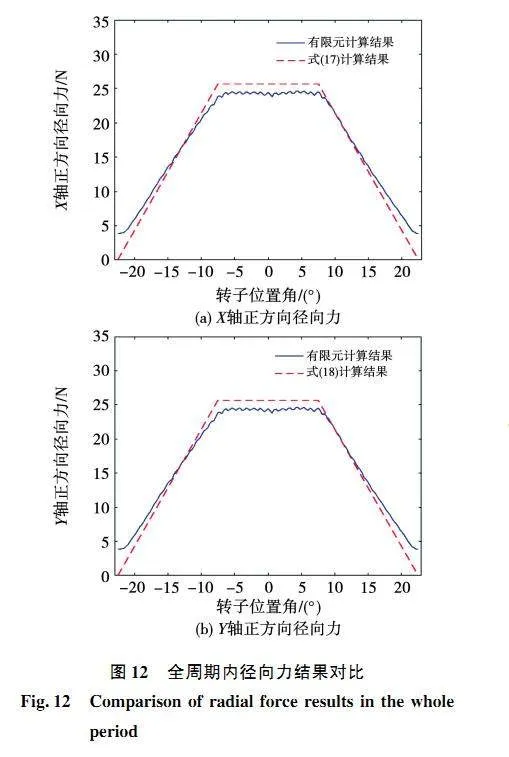
圖12是一個完整周期內的徑向力對比曲線，繞組電流也為iA1=iA3=3 A，iA2=iA4=1 A，其中模型結果由式（17）、式（18）計算得到。可以看出，隨著轉子角θ的變化，模型計算值和有限元計算值能較好吻合。在［-22.5°，-7.5°］區間內，有限元結果與模型推導的結果誤差最大的點在轉子位置角為-7.5°時，此時誤差為7.3%；在［7.5°，22.5°］區間內，有限元結果與模型推導的結果誤差最大的點在轉子位置角為7.5°時，此時誤差為4.71%；當轉子位置角在［-7.5°，7.5°］區間內時，模型計算結果與有限元計算得到的結果整體都很平穩，徑向力平均值的誤差為4.83%。因此，可以說明所建立的全周期徑向力模型是有效的，能夠在一個完整的周期內較準確地描述徑向懸浮力的變化特性。

值得注意的是，雖然在定轉子極重疊區間內的氣隙磁密公式計算結果比三維有限元計算結果大較多，但是定子極邊緣附近的邊緣氣隙磁密計算值相比有限元計算值小較多，因此基于麥克斯韋應力法計算徑向力時，在沿積分路徑積分的過程中，定轉子極重疊區間和不重疊區間內的氣隙磁密誤差相互抵消，最終可獲得更小的徑向力誤差。由于徑向力公式滿足精度，因此也驗證了積分路徑的選擇是恰當的，氣隙磁密計算公式也是有效的。

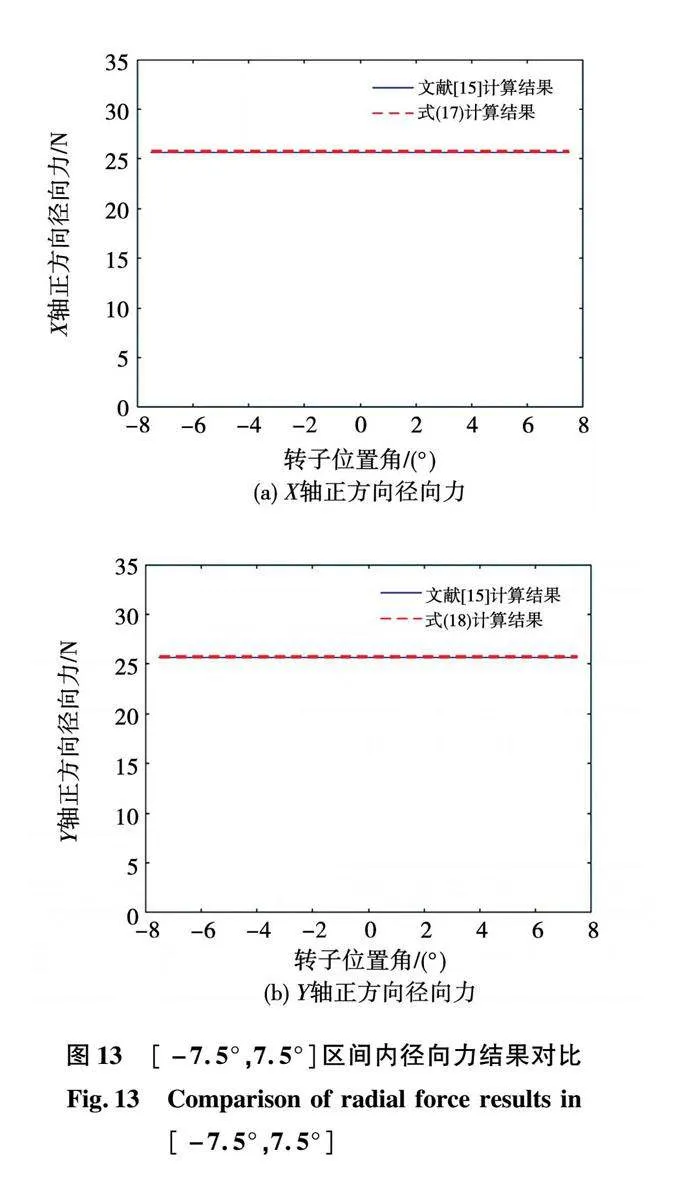
考慮到文獻［15］也建立了定轉子對齊區間的徑向力模型，只是與所用方法不同，因此以相同電機參數以及繞組電流，進一步計算了文獻［15］的徑向力模型計算結果，并進行對比。如圖13所示，在［-7.5°，7.5°］區間內，由2個模型計算出的沿X、Y軸正方向的徑向力大小均為25.69 N，結果一致，說明在此區間可以取得與文獻［15］相同的準確度。

5 結 論

數學模型是電機控制系統設計的基礎。本文針對單繞組BSRMWR在定轉子極非完全交疊區間徑向力模型的空白以及定轉子極完全交疊區間模型推導過程復雜、計算量大的局限性，運用麥克斯韋應力法理論推導了定轉子極非完全交疊區間以及完全交疊區間的徑向懸浮力模型，構成了單繞組BSRMWR一個完整周期全角度的徑向力數學模型，并通過三維有限元數值計算驗證了模型的正確性。該模型是一個未飽和狀態的基礎模型，可用于展開基礎理論研究，驗證基本控制算法，為后續的深入研究提供參考。

參 考 文 獻：

［1］ 胡艷芳， 康智勇， 孫德博， 等. 基于區間分段轉矩分配函數的開關磁阻電機轉矩脈動抑制［J］. 電機與控制學報， 2023， 27（10）： 54.

HU Yanfang， KANG Zhiyong， SUN Debo， et al. Torque ripple suppression of switched reluctance motor based on interval segmentation torque sharing function［J］. Electric Machines and Control， 2023， 27（10）： 54.

［2］ TAKEMOTO M， SUZUKI H， CHIBA A， et al. Improved analysis of a bearingless switched reluctance motor［J］. IEEE Transactions on Industry Applications， 2001， 37（1）： 26.

［3］ CAO Xin， DENG Zhiquan， YANG Gang， et al. Independent control of average torque and radial force in bearingless switched reluctance motors with hybrid excitations［J］. IEEE Transactions on Power Electronics，2009， 24（5）： 1376.

［4］ HAO Zhenyang， CAO Xin， DENG Xu， et al. Novel bearingless switched reluctance motor with wide flat inductance region to simplify the control of torque and levitation force［J］. IEEE Transactions on Energy Conversion， 2020， 35（3）： 1278.

［5］ CHEN L， HOFMANN W. Speed regulation technique of one bearingless 8/6 switched reluctance motor with simpler single winding structure［J］. IEEE Transactions on Industrial Electronics， 2012， 59（6）： 2592.

［6］ LEE D H， WANG Huijun， AHN J W. Modeling and control of novel bearingless switched reluctance motor ［C］// 2009 IEEE Energy Conversion Congress and Exposition， September 20-24， 2009， San Jose， CA， USA. 2009： 276-281.

［7］ GUAN Zhongyu， ZHANG Fengge， AHN J W. High speed direct current compensation control for 8/10 bearingless SRM ［C］// 2012 IEEE International Symposium on Industrial Electronics， May 28-31， 2012， Hangzhou， China. 2012： 1934-1939.

［8］ XU Zhenyao， LEE D H， AHN J W. Suspending force control of a novel 12/14 hybrid stator pole type bearingless SRM ［C］// 15th International Conference on Electrical Machines and Systems， October 21-24， 2012， Sapporo， Japan. 2012： 1-5.

［9］ 曹鑫，李小笛，劉晨昊，等.基于旋轉坐標系的錐形無軸承開關磁阻電機數學模型［J］.電工技術學報，2018，33（17）：4029.

CAO Xin，LI Xiaodi，LIU Chenhao，et al. Mathematical model of conical bearingless switched reluctance motor based on rotating coordinate system［J］. Transactions of China Electrotechnical Society， 2018， 33（17）： 4029.

［10］ WU Xu， YANG Yan， LIU Zeyuan. Analysis and control of a novel bearingless switched reluctance motor with wider rotor teeth［C］// IECON 43rd Annual Conference of the IEEE Industrial Electronics Society， October 29-November 1， 2017， Beijing， China. 2017： 1796-1801.

［11］ 王喜蓮， 崔睿珍， 郝毅，等. 考慮磁飽和的共懸浮繞組式無軸承開關磁阻電機徑向力模型［J］. 電機與控制學報， 2021， 25（6）： 46.

WANG Xilian， CUI Ruizhen， HAO Yi， et al. Radial force model of a bearingless switched reluctance motor with sharing suspension windings considering magnetic saturation［J］. Electric Machines and Control， 2021， 25（6）： 46.

［12］ 嵇小輔， 馬滔， 項倩雯. 8/6極單繞組磁懸浮開關磁阻電機建模與分析［J］. 微電機， 2014， 47（6）： 9.

JI Xiaofu， MA Tao， XIANG Qianwen. Modeling and analysis of 8/6 pole single-winding maglev switched reluctance motor［J］. Micromotor， 2014， 47（6）： 9.

［13］ 王翠， 王喜蓮. 單繞組無軸承開關磁阻電機轉子偏心時懸浮力的分析與計算［J］. 電工電能新技術， 2016， 35（7）： 42.

WANG Cui， WANG Xilian. Analysis and calculation of suspension force for rotor eccentricity of single winding bearingless switched reluctance motor［J］. New Technology of Electrical Engineering and Energy， 2016， 35（7）： 42.

［14］ 孫玉坤， 劉羨飛， 王德明， 等. 基于有限元分析的磁懸浮開關磁阻電機數學模型的全角度拓展［J］. 電工技術學報， 2007， 22（9）： 34.

SUN Yukun， LIU Xianfei， WANG Deming， et al．Extension of mathematical model to full angle for bearingless switched reluctance motors based on finite element analysis［J］. Transactions of China Electrotechnical Society， 2007， 22（9）： 34.

［15］ WU Xu， YANG Yan， LIU Zeyuan. Theoretical analysis and simulation of single winding bearingless switched reluctance generator with wider rotor teeth［J］. International Journal of Applied Electromagnetics and Mechanics， 2018（56）： 387.

［16］ GARRIGAN N R， SOONG W L， STEPHENS C M， et al. Radial force characteristics of a switched reluctance machine ［C］// Proceedings of the 1999 IEEE Industry Applications Conference， October 3-7，1999，Phoenix，AZ， USA.1999（4）：2250-2258.

［17］ 閻秀恪， 謝德馨， 高彰燮， 等. 電磁力有限元分析中麥克斯韋應力法的積分路徑選取的研究［J］. 電工技術學報， 2003， 18（5）： 32.

YAN Xiuke， XIE Dexin， GAO Zhangxie， et al. Research on integration path selection of Maxwell stress tensor method used in electromagnetic force FEM analysis［J］. Transactions of China Electrotechnical Society， 2003， 18（5）： 32.

（編輯：劉琳琳）