以核心問題為引領，發展學生策略意識

吳丹

【摘 要】當前的策略教學注重方法，而弱化策略，學生只知道怎么用，而不知道什么時候用，也不知道為什么用，并且欠缺靈活選擇和運用策略解決問題的意識。文章以蘇教版數學六年級上冊“解決問題的策略—— 假設”一課教學為例，在教學實踐中探索和思考以三個核心問題“用什么”“為什么用”“怎么用”為目標和引領，發展學生策略意識，從而提升其分析問題和解決問題的能力。

【關鍵詞】核心問題 策略意識 策略 假設

“解決問題的策略”是蘇教版數學教材中重要的學習內容，教材從三年級上冊開始，引導學生在解決實際問題的過程中，學習和掌握從條件出發以及從問題出發分析和解決實際問題的策略，并采用列表、畫圖、列舉、轉化、假設的策略和靈活選擇、運用策略解決實際問題。

反思以往的策略教學，注重方法，而弱化策略；學生只知道怎么用，而不知道什么時候用，也不知道為什么用，并且欠缺靈活選擇和運用策略解決問題的策略意識。解決問題，不僅要具備豐富的策略儲備，還要有較強的策略意識，才能靈活地選擇和運用合適的策略解決實際問題。策略教學也不應該僅僅是解決問題，得到結果，還應該著眼于學生在解決問題的過程中獲得策略的體驗，感悟策略的價值，發展策略意識，從而提升分析問題和解決問題的能力。筆者以蘇教版數學六年級上冊第四單元的“解決問題的策略——假設”一課的教學為例，談一談自己的教學實踐和思考。

一、在情境中明確目標，感悟策略價值

《義務教育數學課程標準（2022年版）》指出，要引導學生在真實情境中發現問題和提出問題、分析問題和解決問題。創設真實有效的情境，能激發學生學習的興趣，讓課堂更加鮮活，同時真實有效的情境也能讓學生有更加豐富的體驗。針對策略教學中注重方法而弱化策略的問題，教師可以創設生動有趣的情境，使學生通過情境感悟策略的價值，產生策略需求。

【案例】

自主導向，明確目標

1.談話

師：先來聽一個故事。（電腦播放《田忌賽馬》視頻）

2.提問

師：聽了這個故事，你想到了什么？

師：孫臏用了什么策略？

生1：調換了馬的出場順序。

師：為什么用這個策略？

生2：因為田忌的馬弱。

師：怎樣用這個策略解決問題？

生3：上等馬對中等馬，中等馬對下等馬，下等馬對上等馬。

師板書：“用什么”“為什么用”“怎樣用”

3.回顧

師：運用一種合適的策略往往能收到事半功倍的效果，我們已經學過哪些解決問題的策略？

4.總結

師：這兩種策略可以幫助我們更好地分析數量關系，列表和畫圖能幫助我們整理信息，以便更好地分析數量關系；列舉和轉化的策略主要用來解決特殊問題。

學生說到轉化，教師就可以相機提問：我們為什么用轉化的策略來解決問題？（復雜轉化為簡單，新知轉化為舊知）

5.明確目標

師：這節課，我們繼續學習解決問題的策略。通過學習，我們要明確用了什么策略，然后還要達成哪些學習目標。

師：帶著這些學習目標，我們開始今天的學習。

教師利用學生耳熟能詳的《田忌賽馬》的故事情境來引入本課的教學，旨在拋磚引玉出三個核心問題“用什么”“為什么用”“怎么用”，引導學生關注策略本身，讓學生有更切身的策略體驗，深刻感悟策略的價值和需求，形成策略意識。同時在后續學習假設策略的過程中，教師也要始終以這三個核心問題為目標和引領，引導學生在用假設的策略解決問題的過程中，明確什么時候用假設的策略，為什么用假設的策略，以及怎么用假設的策略，不斷感受策略的價值，發展策略意識。

二、在對比中建構模型，發現策略本質

數學學習是建立和完善個體數學認知結構的過程，數學認知結構由數學知識結構轉化而來，學生將數學知識結構內化在頭腦中，就形成個體的認知結構。而學生能將數學知識結構轉化為個體大腦里的數學認知結構，需要學生對數學知識結構有本質的認識。六年級學生雖然具備一定的抽象能力，但一題一題零散化地學習，不利于學生發現這些實際問題中隱含的數學本質。雖然大部分學生對怎么用假設的策略來解決問題已經有了比較豐富的感悟和實踐，但對于什么樣的實際問題可以用假設的策略來解決還是比較模糊的，他們的認識僅僅停留在有兩個未知量的實際問題能用假設的策略來解決這樣比較淺的層面。此時，教師可以引導學生充分觀察和比較例題，并進行練習，異中求同，發現策略本質，從而發展學生的策略意識。

【案例】

1.在比較中建構模型

師：比較一下，怎樣的題目適合用假設的策略來解決？

生1：有兩個未知量。

生2：已知兩個未知量的和。（電腦橙色顯示）

追問：還有嗎？

生3：已知這兩個未知量的倍比關系，求的問題都是這兩個未知量分別是幾。（電腦藍色顯示）

師：看來，像這樣，已知兩個未知量的和與倍數關系的和倍問題適合用假設的策略來解決。

2.在對比中應用模型

教師出示3道題（見圖1）。

圖1

師：選一選，這3道題中哪些可以運用假設的策略解決？你是怎么想的？

生1：我覺得第（1）題可以用假設的策略，因為題目中告訴了我們大貨車和小貨車運的噸數一共是20噸，還知道大貨車運的是小貨車的2倍，是一個和倍問題

師：還有嗎？

生2：我覺得第（3）題也可以用假設的策略來解決，第1個算式表示x和y這兩個未知量的和是72，第2個算式表示x是y的5倍，這樣就可以用假設的策略求出x和y分別是幾。

師：第（2）題能用假設的策略解決嗎？你是怎么想的？

生3：第（2）題不需要用假設的策略來解決，因為上衣的價錢是已知的。

通過對比，學生“剝離”和“去除”了具體的情境，抽象出了例題和練一練這兩個同結構實際問題的共同點，都是已知兩個未知量的和與倍比關系，都是求兩個未知量分別是多少。學生在對比中明晰了這一類實際問題的數學本質，將這一類實際問題的知識結構轉化為自己頭腦中的認知結構，順利建構模型，在后續解決相關問題時，就能更好地分析和識別模型。這樣的對比，讓學生不僅知道怎么用假設的策略來解決實際問題，也知道了什么時候用假設的策略，以及為什么要用假設的策略。學生知其然，更知其所以然，充分感悟了假設策略的本質，發展了策略意識。

二、勾連中完善認知結構，豐富策略認識

數學學科知識之間有著緊密的聯系，勾連新知和舊知，構建新舊知識之間的聯系，將內容結構化，形成完整的數學學科知識結構，有助于學生完善原有的認知結構。學生運用假設的策略解決和倍問題后，就對假設策略有了一定的認識和體驗，但這樣的認識和體驗還不夠全面，學生很容易誤以為假設的策略只能解決和倍問題。為了讓學生對假設策略形成更全面、更豐富的認識，教師可以引導學生聯系以前學過的簡單的差倍問題、和差問題，引出將要學習的復雜的差倍問題，讓學生對假設策略形成更加豐富的認識和體驗。

【案例】

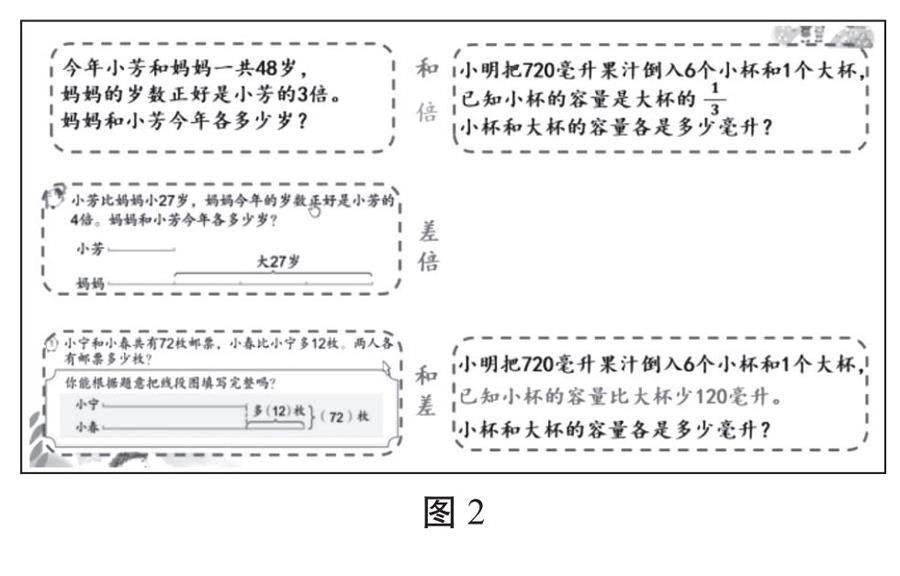
師：其實，在我們以前的學習中也用到了假設的策略，現在你知道是如何使用假設的策略嗎？（出示簡單的倍和問題，見圖2）

圖2

生1：假設媽媽的歲數是3個小芳的歲數。

師：除了和倍問題能用假設的策略解決，你還想到了什么？

生2：我還想到了差倍問題、和差問題。

師：差倍問題、和差問題是不是也用到了假設的策略呢？如果用到了，又是怎么假設的？（電腦出示簡單的差倍問題和相差問題）

生3：差倍問題里也用到了假設的策略，可以假設媽媽的歲數是3個小芳的歲數。

師：那和差問題呢？

生4：和差問題也用到了假設的策略，假設小春和小寧的郵票同樣多。

師：如果把例題中“小杯的容量是大杯的”這個條件改成“小杯的容量比大杯少120毫升”，這個和差問題能用假設的策略來解決嗎？怎么假設呢？（電腦出示稍復雜的差倍問題）

生5：我覺得可以用假設的策略來解決，把一個大杯假設成小杯加120毫升，或者把一個小杯假設成大杯減120毫升。

在幫助學生通過對比構建模型并運用模型選擇了適合用假設的策略解決實際問題后，教師引導學生勾連以前學過的簡單的“和倍問題”“差倍問題”“和差問題”，思考能不能用假設的策略，以及怎么用假設的策略，打破了學生原有的認知結構，這樣破而后立的設計，將數學學科知識結構化，不僅幫助學生形成了更加完整、深刻的認知結構，也豐富了學生對假設這一策略的認識和體驗。

在“解決問題的策略——假設”一課的教學中，筆者始終以“用什么”“為什么用”“怎么用”這3個核心問題為目標和引領，在分析和解決問題的過程中，關注情境的創設、數量關系的分析和理解，重視引導學生對比和反思，設計讓學生多角度、多層次地去體驗策略，發展策略意識。總之，解決問題的策略教學，既要解決問題，也要在解決問題的過程中感悟策略的價值，發展策略意識，從而在解決實際問題時，能根據不同的實際問題，靈活選擇和運用策略，提升學生分析問題和解決問題的能力，這才是策略教學的意義和價值。

【參考文獻】

[1]孫冬梅. 以問題解決為抓手，發展學生的策略意識——“用列舉的策略解決問題”教學評析[J]. 小學數學教育， 2020（24）.

[2]蘇蓉蓉. 豐盈思考過程，形成策略意識——以“解決問題的策略——假設”教學為例[J]. 小學教學參考（數學）， 2021（11）.