極值點(diǎn)偏移問題的探源、拓展及應(yīng)用
程漢波 黃嵩濤


【摘? 要】? “極值點(diǎn)偏移問題”作為導(dǎo)數(shù)在研究函數(shù)性質(zhì)中的應(yīng)用之一,近年來在教研中受到廣泛關(guān)注.利用泰勒展開這一工具探究后得出:極值點(diǎn)偏移問題是中值點(diǎn)偏移問題的特殊情形,滿足羅爾中值定理(或拉格朗日中值定理)條件的至少三階可導(dǎo)函數(shù)中可能會(huì)存在“極值點(diǎn)偏移”(或“中值點(diǎn)偏移”)現(xiàn)象,而且,在其三階導(dǎo)數(shù)恒為0時(shí),極值點(diǎn)(或中值點(diǎn))不偏;在三階導(dǎo)數(shù)不為零且正負(fù)性確定的條件下,當(dāng)二階導(dǎo)數(shù)與三階導(dǎo)數(shù)乘積的為正時(shí),極值點(diǎn)(或中值點(diǎn))右偏;當(dāng)二階導(dǎo)數(shù)與三階導(dǎo)數(shù)乘積的為負(fù)時(shí),極值點(diǎn)(或中值點(diǎn))左偏.最后利用探究所得的結(jié)果解答三道全國(guó)卷中出現(xiàn)的極值點(diǎn)偏移問題,并給出關(guān)于高觀點(diǎn)對(duì)中學(xué)數(shù)學(xué)教學(xué)作用的一點(diǎn)感悟.
【關(guān)鍵詞】? 極值點(diǎn)偏移;泰勒展開;三階導(dǎo)數(shù);中值點(diǎn)偏移
“極值點(diǎn)偏移問題”作為導(dǎo)數(shù)在研究函數(shù)性質(zhì)中的應(yīng)用之一,近年來在教研中受到廣泛關(guān)注,在“中國(guó)知網(wǎng)”以“極值點(diǎn)偏移”為主題進(jìn)行搜索可發(fā)現(xiàn),僅標(biāo)題中含有“極值點(diǎn)偏移”字樣的文獻(xiàn)就有逾200篇,但細(xì)看不難發(fā)現(xiàn),以“例題+解法”居多,如構(gòu)造對(duì)稱函數(shù)、利用對(duì)數(shù)平均不等式、比值代換法等處理策略在教研中得到廣泛普及且變得愈發(fā)成熟.然而,教研文章的數(shù)量并不意味著對(duì)極值點(diǎn)偏移問題的研究已算圓滿.恰恰相反,之所以會(huì)有如此多的文章探究這類問題,在一定程度上說明大家對(duì)其已有的研究并不完全滿意.而且,解法的普及與成熟也說明這類問題具有較強(qiáng)的共性,理應(yīng)進(jìn)一步抽象概括出通用解法背后的深層本質(zhì).
1? 極值點(diǎn)偏移問題簡(jiǎn)介
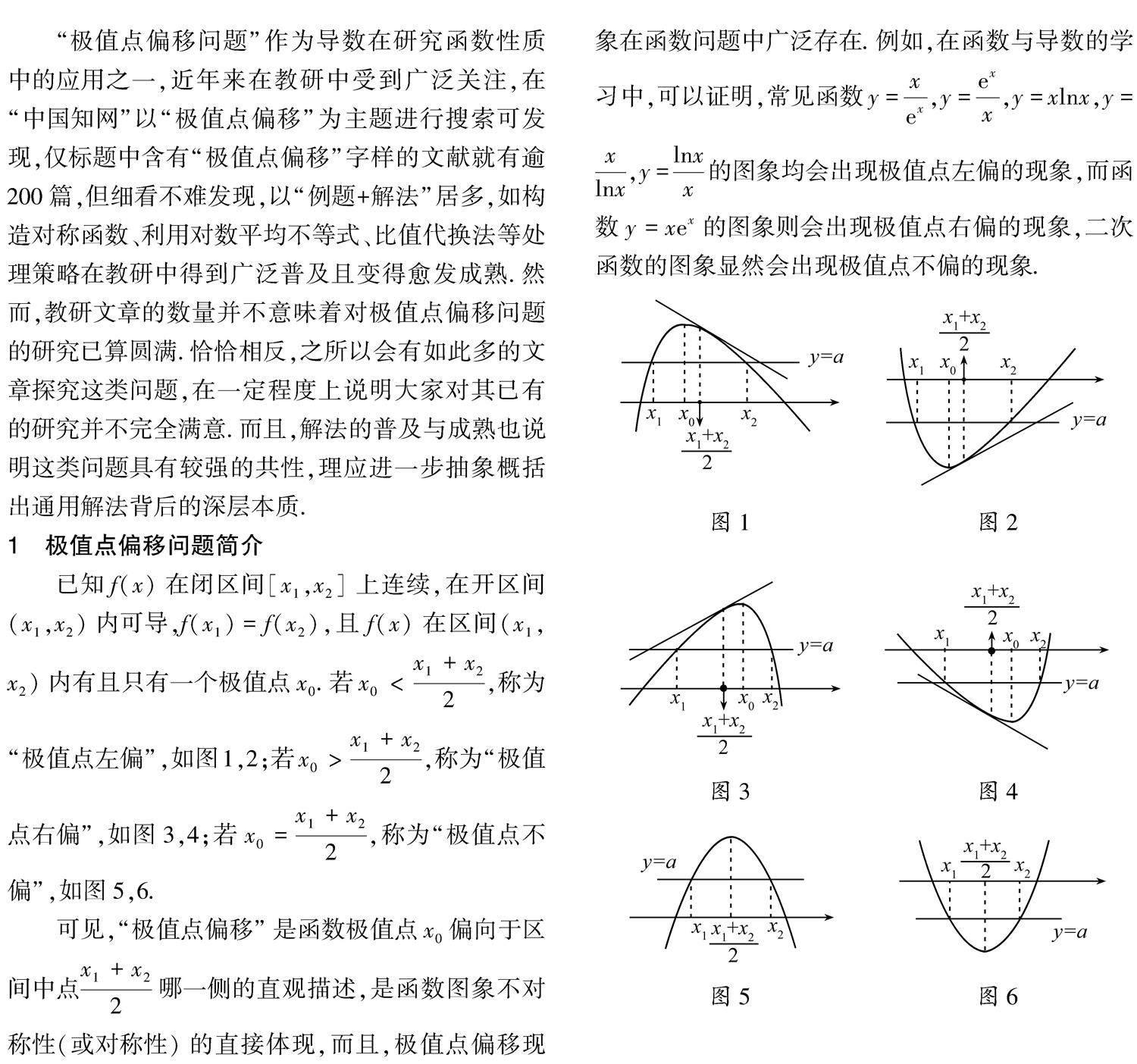
已知f(x)在閉區(qū)間[x1,x2]上連續(xù),在開區(qū)間(x1,x2)內(nèi)可導(dǎo),f(x1)=f(x2),且f(x)在區(qū)間(x1,x2)內(nèi)有且只有一個(gè)極值點(diǎn)x0.若x0<x1+x22,稱為“極值點(diǎn)左偏”,如圖1,2;若x0>x1+x22,稱為“極值點(diǎn)右偏”,如圖3,4;若x0=x1+x22,稱為“極值點(diǎn)不偏”,如圖5,6.可見,“極值點(diǎn)偏移”是函數(shù)極值點(diǎn)x0偏向于區(qū)間中點(diǎn)x1+x22哪一側(cè)的直觀描述,是函數(shù)圖象不對(duì)稱性(或?qū)ΨQ性)的直接體現(xiàn),而且,極值點(diǎn)偏移現(xiàn)象在函數(shù)問題中廣泛存在.例如,在函數(shù)與導(dǎo)數(shù)的學(xué)習(xí)中,可以證明,常見函數(shù)y=xex,y=exx,y=xlnx,y=xlnx,y=lnxx的圖象均會(huì)出現(xiàn)極值點(diǎn)左偏的現(xiàn)象,而函數(shù)y=xex的圖象則會(huì)出現(xiàn)極值點(diǎn)右偏的現(xiàn)象,二次函數(shù)的圖象顯然會(huì)出現(xiàn)極值點(diǎn)不偏的現(xiàn)象.
2? 極值點(diǎn)偏移問題探源
要比較極值點(diǎn)x0與區(qū)間中點(diǎn)x1+x22的大小,注意到f′(x0)=0,故可以先判斷出f′x1+x22的正負(fù)性,再根據(jù)f′(x)的單調(diào)性(由f″(x)的正負(fù)性決定)得出x1+x22與x0的大小關(guān)系.由圖1—6可以大致猜測(cè),極值點(diǎn)偏移規(guī)律與函數(shù)的單調(diào)性(一階導(dǎo)數(shù)刻畫)及函數(shù)的凹凸性(二階導(dǎo)數(shù)刻畫)有關(guān),因?yàn)楹瘮?shù)圖象的不對(duì)稱性(或?qū)ΨQ性)本身就與其單調(diào)性、凹凸性聯(lián)系緊密.然而,也不難發(fā)現(xiàn),圖1,3,5中函數(shù)均為上凸函數(shù),且先增后減,但卻出現(xiàn)了不同的極值點(diǎn)偏移現(xiàn)象;同樣地,圖2,4,6中函數(shù)均為下凸函數(shù),且先減后增,也出現(xiàn)了不同的極值點(diǎn)偏移現(xiàn)象.這表明直接由圖1—6歸納出極值點(diǎn)偏移規(guī)律稍顯困難,還需更精細(xì)化的考察,下面用泰勒展開這一高等數(shù)學(xué)工具探究f′x1+x22的正負(fù)性的判定條件,并進(jìn)一步得到極值點(diǎn)偏移規(guī)律更本源的刻畫方式,具體過程與結(jié)果如下.
假定f(x)至少三階可導(dǎo),記m=x1+x22,將f(x1)與f(x2)分別在x=m處泰勒展開得,
f(x1)=f(m)+f′(m)(x1-m)+f″(m)2(x1-m)2+f(ξ1)6(x1-m)3(x1<ξ1<m);
f(x2)=f(m)+f′(m)(x2-m)+f″(m)2(x2-m)2+f(ξ2)6(x2-m)3(m<ξ2<x2).
因?yàn)閒(x1)=f(x2),將以上兩式相減可解得,
f′(m)=-f(ξ1)+f(ξ2)48·(x1-x2)2.(*)
(1)當(dāng)f(x)=0時(shí),由于f(x)在區(qū)間(x1,x2)內(nèi)只有一個(gè)極值點(diǎn)x0,因此f″(x)為非零常數(shù),則f′(x)為單調(diào)函數(shù).由(*)式知,f′(m)=0=f′(x0),所以m=x1+x22=x0.
(2)當(dāng)f(x)>0時(shí),由(*)式知,f′(m)<0=f′(x0),則
①當(dāng)f″(x)>0時(shí),f′(x)單調(diào)遞增,則m=x1+x22<x0;
②當(dāng)f″(x)<0時(shí),f′(x)單調(diào)遞減,則m=x1+x22>x0.
(3)當(dāng)f(x)<0時(shí),由(*)式知,f′(m)>0=f′(x0),則
①當(dāng)f″(x)>0時(shí),f′(x)單調(diào)遞增,則m=x1+x22>x0;
②當(dāng)f″(x)<0時(shí),f′(x)單調(diào)遞減,則m=x1+x22<x0.
綜上所述,當(dāng)f(x)=0時(shí),x1+x22=x0;當(dāng)f(x)·f″(x)>0時(shí),x1+x22<x0;當(dāng)f(x)·f″(x)<0時(shí),x1+x22>x0.
值得一提的是,以上綜述結(jié)果中f(x)·f″(x)>0是指f″(x)>0,f(x)>0或f″(x)<0,f(x)<0兩種情形,并不包括f″(x)或f″(x)的正負(fù)性不完全確定的情形;類似地,f(x)·f″(x)<0是指f″(x)>0,f(x)<0或f″(x)<0,f(x)>0兩種情形.下文與之類似,不再贅述.
因此,至少三階連續(xù)可導(dǎo)函數(shù)的極值點(diǎn)偏移問題可用其二階導(dǎo)數(shù)與三階導(dǎo)數(shù)共同刻畫.具體地,三階導(dǎo)數(shù)是否為0可斷定極值點(diǎn)是否會(huì)發(fā)生偏移,在三階導(dǎo)數(shù)不為零且正負(fù)性確定的條件下,二階導(dǎo)數(shù)與三階導(dǎo)數(shù)乘積的正負(fù)性可斷定是極值點(diǎn)左偏還是極值點(diǎn)右偏.例如,二次函數(shù)的三階導(dǎo)數(shù)恰好等于0,會(huì)出現(xiàn)“極值點(diǎn)不偏”的現(xiàn)象,這與其圖象是軸對(duì)稱圖形的直觀相一致;函數(shù)y=xlnx的二階、三階導(dǎo)數(shù)分別為y″=1x>0, y=-1x2<0,則
y″y=-1x3<0,這與其圖象在區(qū)間0,1上會(huì)出現(xiàn)“極值點(diǎn)左偏”(即x0=1e<x1+x22)的現(xiàn)象相一致;函數(shù)f(x)=xex的二階、三階導(dǎo)數(shù)分別為f″(x)=(x+2)ex,f(x)=
(x+3)ex,則f″(x)·f(x)=(x+2)(x+3)e2x,由f(x1)=f(x2)可推得x1,x2<0,當(dāng)x1,x2中有變量小于等于-2時(shí),“極值點(diǎn)右偏”(即x0=-1>x1+x22)顯然成立;當(dāng)-2<x1,x2<0時(shí),有f″(x)>0, f(x)>0,則f″(x)f(x)>0,“極值點(diǎn)右偏”也成立.因此,這三個(gè)特例恰好印證了前面所得的結(jié)論.
3? 極值點(diǎn)偏移問題拓展
由極值點(diǎn)偏移問題的條件和結(jié)論不難聯(lián)想起羅爾中值定理:若閉區(qū)間[x1,x2]上的連續(xù)函數(shù)f(x)在開區(qū)間(x1,x2)內(nèi)可導(dǎo),且f(x1)=f(x2),則在(x1,x2)內(nèi)至少存在一點(diǎn)ξ(稱其為中值點(diǎn)),使得f′(ξ)=0.上文討論結(jié)果表明,在中值點(diǎn)唯一的前提下,有時(shí)可以根據(jù)f(x)的二階導(dǎo)數(shù)f″(x)與三階導(dǎo)數(shù)f(x)的正負(fù)性,得到中值點(diǎn)ξ與區(qū)間中點(diǎn)x1+x22的大小關(guān)系.因此,極值點(diǎn)偏移問題也可以看作中值點(diǎn)偏移問題的特殊情形,都是比較極值點(diǎn)(或中值點(diǎn))ξ與區(qū)間中點(diǎn)x1+x22的大小關(guān)系,進(jìn)而得出極值點(diǎn)(或中值點(diǎn))ξ相對(duì)于區(qū)間中點(diǎn)x1+x22的偏移方向,它是對(duì)羅爾中值定理中存在性結(jié)果的進(jìn)一步深入細(xì)致的探究.
于是,不禁又聯(lián)想起拉格朗日中值定理:若閉區(qū)間[x1,x2]上的連續(xù)函數(shù)f(x)在開區(qū)間(x1,x2)內(nèi)可導(dǎo),則在(x1,x2)內(nèi)至少存在一點(diǎn)ξ,使得f′(ξ)=f(x2)-f(x1)x2-x1.在中值點(diǎn)ξ唯一的條件下,能否類似地探究中值點(diǎn)ξ與區(qū)間中點(diǎn)x1+x22的大小關(guān)系呢?不難發(fā)現(xiàn),該問題是極值點(diǎn)偏移問題的拓展推廣,它的解決可以進(jìn)一步的揭示極值點(diǎn)偏移問題的本質(zhì).經(jīng)歷一番探究,得到以下結(jié)果:
定理? 若閉區(qū)間[x1,x2]上的連續(xù)函數(shù)f(x)在(x1,x2)內(nèi)至少三階可導(dǎo),且f′(x)不為常數(shù),則
(1)若f(x)=0,則存在唯一ξ=x1+x22,使得f′(ξ)=f(x2)-f(x1)x2-x1;
(2)若f(x)·f″(x)>0,則存在唯一ξ∈x1+x22,x2,使得f′(ξ)=f(x2)-f(x1)x2-x1;
(3)若f(x)·f″(x)<0,則存在唯一ξ∈x1,x1+x22,使得f′(ξ)=f(x2)-f(x1)x2-x1.
證明? 記x1+x22=m,將f(x1)與f(x2)分別在x=m處泰勒展開得,
f(x1)=f(m)+f′(m)(x1-m)+f″(m)2(x1-m)2+f(ξ1)6(x1-m)3(x1<ξ1<m);
f(x2)=f(m)+f′(m)(x2-m)+f″(m)2(x2-m)2+f(ξ2)6(x2-m)3(m<ξ2<x2).
將以上兩式相減可得,
f(x1)-f(x2)=f′x1+x22(x1-x2)+f(ξ1)+f(ξ2)48(x1-x2)3.
在區(qū)間[x1,x2]上由拉格朗日中值定理知,存在ξ∈(x1,x2),使得
f′(ξ)=f(x1)-f(x2)x1-x2=f′x1+x22+f(ξ1)+f(ξ2)48(x1-x2)2.(**)
(1)當(dāng)f(x)=0時(shí),結(jié)合f′(x)不為常數(shù),則f″(x)為非零常數(shù),因此f′(x)為單調(diào)函數(shù).由(**)式知,f′(ξ)=f′x1+x22,所以存在唯一ξ=x1+x22.
(2)當(dāng)f(x)·f″(x)>0時(shí),則可分兩種情況:
①當(dāng)f(x)>0, f″(x)>0時(shí),由(**)知,f′(ξ)>f′x1+x22,且f′(x)單調(diào)遞增,所以存在唯一ξ∈x1+x22,x2;
②當(dāng)f(x)<0, f″(x)<0時(shí),由(**)知,f′(x0)<f′x1+x22,且f′(x)單調(diào)遞減,所以也存在唯一ξ∈x1+x22,x2.
(3)與(2)類似可證,此處略去.
由此可知,極值點(diǎn)偏移問題確實(shí)就是中值點(diǎn)偏移問題的特殊情形,任何滿足拉格朗日中值定理?xiàng)l件的函數(shù)中均可能會(huì)存在中值點(diǎn)偏移現(xiàn)象.具體地,對(duì)于滿足拉格朗日中值定理?xiàng)l件且至少三階可導(dǎo)的函數(shù),其三階導(dǎo)數(shù)是否為0可斷定中值點(diǎn)是否會(huì)發(fā)生偏移,在三階導(dǎo)數(shù)不為零且正負(fù)性確定的條件下,二階導(dǎo)數(shù)與三階導(dǎo)數(shù)乘積的正負(fù)性可斷定中值點(diǎn)是左偏還是右偏.例如,對(duì)于對(duì)數(shù)函數(shù)f(x)=lnx,其二階、三階導(dǎo)數(shù)分別為f″(x)=-1x2<0, f(x)=2x3>0,則f″(x)·f(x)<0,因此會(huì)出現(xiàn)“中值點(diǎn)左偏”的現(xiàn)象,即存在唯一ξ∈x1,x1+x22,使得f′(ξ)=f(x2)-f(x1)x2-x1=lnx2-lnx1x2-x1.又因?yàn)閒′(x)=1x單調(diào)遞減,所以f′(ξ)>f′x1+x22,即lnx2-lnx1x2-x1>2x1+x2,該不等式即為“對(duì)數(shù)平均不等式”的一部分,它在解決與自然對(duì)數(shù)有關(guān)的“極值點(diǎn)偏移問題”屢建奇功,在教學(xué)、教研中已發(fā)展為一種重要的策略工具.由此觀之,“對(duì)數(shù)平均不等式”之所以會(huì)如此有效,部分原因是因?yàn)樵摻Y(jié)果就是對(duì)數(shù)函數(shù)中“中值點(diǎn)偏移問題”的代數(shù)刻畫,當(dāng)然可在“極值點(diǎn)(即中值點(diǎn))偏移問題”中大放異彩.類似地,對(duì)指數(shù)函數(shù)f(x)=ex,不難由“中值點(diǎn)偏移問題”的結(jié)果得ex1-ex2x1-x2>ex1+x22,也有人將其稱為“指數(shù)平均不等式”,它在解決指數(shù)函數(shù)有關(guān)的“極值點(diǎn)(即中值點(diǎn))偏移問題”時(shí)也照樣大放異彩.
4? 高考中的極值點(diǎn)偏移問題
近些年來,極值點(diǎn)偏移問題的例子眾多,筆者在教學(xué)實(shí)踐中發(fā)現(xiàn),大都可用以上結(jié)論解決,既簡(jiǎn)明快捷又貼近本質(zhì).本文僅給出全國(guó)高考卷中對(duì)極值點(diǎn)偏移問題的研究熱點(diǎn)“推波助瀾”的三道高考題及解答,更多的例子讀者在實(shí)踐中可不斷嘗試.
例1? (2016年全國(guó)高考新課標(biāo)Ⅰ卷(乙卷)第21題)已知函數(shù)f(x)=(x-2)ex+a(x-1)2有兩個(gè)零點(diǎn).
(Ⅰ)求a的取值范圍;
(Ⅱ)設(shè)x1,x2是f(x)的兩個(gè)零點(diǎn),證明:x1+x2<2.
證明? ?(Ⅰ)a>0,過程略;(Ⅱ)由(Ⅰ)知,a>0,且x1<1<x2<2,則
①當(dāng)x1<0時(shí),由x2<2得,x1+x2<2;
②當(dāng)x1≥0時(shí),f′(x)=(x-1)ex+2a, f″(x)=xex+2a, f(x)=x+1ex,則當(dāng)x∈[x1,x2]時(shí),有f″(x)>0, f(x)>0,則f″(x)·f(x)>0,所以x1+x22<1,即x1+x2<2.
例2? (2021年全國(guó)新高考Ⅰ卷第22題)已知函數(shù)f(x)=x(1-lnx).
(Ⅰ)討論f(x)的單調(diào)性;
(Ⅱ)設(shè)a,b為兩個(gè)不相等的正數(shù),且blna-alnb=a-b,證明:1a+1b>2.
證明? (Ⅰ)略;(Ⅱ)由(Ⅰ)知,f(x)在(0,1)上單調(diào)遞增,在(1,+∞)上單調(diào)遞減.注意到blna-alnb=a-b即為f1a=f1b,不妨設(shè)1a=x1∈(0,1),1b=x2∈(1,+∞),則原問題等價(jià)于證明x1+x2>2.
①當(dāng)x2≥2時(shí),由x1>0得,x1+x2>2;
②當(dāng)x2<2時(shí),f′(x)=-lnx, f″(x)=-1x, f(x)=1x2,則當(dāng)x∈[x1,x2]時(shí),有f″(x)<0, f(x)>0,則f″(x)·f(x)<0,所以x1+x22>1,即x1+x2>2.
例3? (2022年全國(guó)高考甲卷第21題)已知函數(shù)f(x)=exx-lnx+x-a.
(Ⅰ)f(x)≥0,求a的取值范圍;
(Ⅱ)若f(x)存在兩個(gè)零點(diǎn)x1,x2,證明:x1x2<1.
證明? (Ⅰ)略;(Ⅱ)由f(x1)=f(x2)得,ex1x1-lnx1+x1-a=ex2x2-lnx2+x2-a,即ex1x1+lnex1x1=ex2x2+lnex2x2.記g(x)=x+lnx,則gex1x1=gex2x2.易知g(x)單調(diào)遞增,則ex1x1=ex2x2,兩邊取自然對(duì)數(shù)得,x1-lnx1=x2-lnx2.注意到x1,x2>0,要證明x1x2<1,只需證明lnx1+lnx2<0,又記h(x)=ex-x,則hlnx1=hlnx2,且h′(x)=ex-1,h″(x)=h(x)=ex>0,則h″(x)·h(x)>0,所以lnx1+lnx22<0,即x1x2<1.
5? 余話與啟示
眾所周知,微積分的誕生與運(yùn)動(dòng)學(xué)息息相關(guān).例如,位移對(duì)時(shí)間的一階導(dǎo)數(shù)是速度,用以描述運(yùn)動(dòng)的快慢;位移對(duì)時(shí)間的二階導(dǎo)數(shù)是加速度,用以描述速度變化的快慢.不禁產(chǎn)生疑問:位移對(duì)時(shí)間的三階導(dǎo)數(shù)及其物理意義是什么呢?由文[3][4]可知,牛頓力學(xué)框架體系對(duì)加速度的變化并未給出任何實(shí)質(zhì)性的描述,但隨著汽車、火車、公路、鐵路等人類物質(zhì)文明的發(fā)展,到19世紀(jì)中葉,人們認(rèn)識(shí)到加速度的變化快慢會(huì)引起舒適感的不同,這與機(jī)械元件(如凸輪、軌道)的設(shè)計(jì)有關(guān),于是將位移對(duì)時(shí)間的三階導(dǎo)數(shù)稱為急動(dòng)度,用以描述加速度的變化快慢.
同樣地,微積分的誕生與幾何學(xué)也息息相關(guān).例如,函數(shù)的一階導(dǎo)數(shù)的幾何意義為切線斜率,用以描述函數(shù)的單調(diào)性;函數(shù)的二階導(dǎo)數(shù)可以表示切線斜率的變化快慢,用以描述函數(shù)的凹凸性.不禁產(chǎn)生疑問:函數(shù)的三階導(dǎo)數(shù)及其幾何意義是什么呢?它描述了函數(shù)哪方面的性質(zhì)呢?本文探究得出,極值點(diǎn)偏移問題是中值點(diǎn)偏移問題的特殊情形,對(duì)于滿足拉格朗日中值定理(或羅爾中值定理)條件且至少三階可導(dǎo)的函數(shù),其三階導(dǎo)數(shù)是否為0可斷定中值點(diǎn)是否會(huì)發(fā)生偏移,在三階導(dǎo)數(shù)不為零且正負(fù)性確定的條件下,二階導(dǎo)數(shù)與三階導(dǎo)數(shù)乘積的正負(fù)性可斷定是中值點(diǎn)左偏還是中值點(diǎn)右偏.
用泰勒展開式的觀點(diǎn)來看極值點(diǎn)(或中值點(diǎn))偏移問題,它不僅提供了解決問題的一種策略,也是命制相關(guān)試題的一條渠道.更深入地揭示這類問題的本質(zhì).這啟示我們中學(xué)教師應(yīng)主動(dòng)探尋初等數(shù)學(xué)與高等數(shù)學(xué)知識(shí)的結(jié)合點(diǎn),從而對(duì)中學(xué)數(shù)學(xué)知識(shí)有一個(gè)更深層次的理解.教師只有站在較高的角度審視數(shù)學(xué)問題,才能將問題看得更清楚,更透徹.這正如F·克萊因所認(rèn)為的,“教師掌握的知識(shí)要比他所教的多得多,才能引導(dǎo)學(xué)生繞過懸?guī)r,渡過險(xiǎn)灘”.
德國(guó)哥廷根數(shù)學(xué)學(xué)派領(lǐng)袖菲利克斯·克萊因曾說:“數(shù)學(xué)教師應(yīng)站在更高(高等數(shù)學(xué))視角審視、理解初等數(shù)學(xué)問題,只有觀點(diǎn)高了,事物才能顯得明了而簡(jiǎn)單;有許多初等數(shù)學(xué)的現(xiàn)象只有在非初等的理論結(jié)構(gòu)內(nèi)才能深刻地理解.”杜甫詩云:“會(huì)當(dāng)凌絕頂,一覽眾山小”.就事論事地看待中學(xué)數(shù)學(xué),只是知其然,用高等數(shù)學(xué)的數(shù)學(xué)方法進(jìn)行解讀,就會(huì)豁然開朗,不僅知其然,更知其所以然.我國(guó)有一句著名教育格言“要給學(xué)生一杯水,教師應(yīng)該有一桶水”,說的也是這層意思.
參考文獻(xiàn)
[1]? 甘大旺.函數(shù)極值點(diǎn)偏移問題新論[J].?dāng)?shù)學(xué)通訊:下半月,2017(07):44-47.
[2]? 朱華偉,程漢波,楊春波.2016年全國(guó)卷Ⅰ壓軸題的解法賞析、探究與思考[J].?dāng)?shù)學(xué)通訊:下半月,2017(11):26-30.
[3]? 黃沛天.一個(gè)描寫機(jī)械運(yùn)動(dòng)的新概念:急動(dòng)度[J].物理,1981(07):394-397.
[4]? 黃沛天,黃文,胡利云.變加速運(yùn)動(dòng)理論與實(shí)踐意義初探[J].江西師范大學(xué)學(xué)報(bào)(自然科學(xué)版),2003(01):8-11.
[5]? 陳月蘭.高觀點(diǎn)下的初等數(shù)學(xué)[M].上海:上海華東師范大學(xué)出版社,2011.
作者簡(jiǎn)介
程漢波(1990—),男,湖北孝感人,博士,高中數(shù)學(xué)一級(jí)教師,主要從事數(shù)學(xué)教育研究.
黃嵩濤(1989—),男,湖北武漢人,博士研究生,高中數(shù)學(xué)一級(jí)教師,主要從事數(shù)學(xué)教育研究.

