帕斯卡定理背景下圓錐曲線問題的命制與解答

唐宜鐘 楚豪

【摘? 要】? 文章給出了帕斯卡定理及其退化形式、特殊情況和逆定理，并通過具體實例分析了帕斯卡定理背景下圓錐曲線問題的命制與解答.

【關鍵詞】? 帕斯卡定理；圓錐曲線；問題命制

近年來，高考要求“創(chuàng)新試題設計，加強關鍵能力考查，突出理性思維，發(fā)揮數學學科高考的選拔功能”［1］.遵循這一要求，2023年北京卷率先嘗試以帕斯卡定理為背景進行圓錐曲線問題的命題.基于此，筆者嘗試對帕斯卡定理背景下的圓錐曲線問題進行了挖掘.

1? 帕斯卡定理

1.1? 帕斯卡定理

圖1帕斯卡定理于公元1639年為法國數學家布萊士·帕斯卡所發(fā)現，其描述為：如圖1，設ABCDEF內接于圓（與頂點次序無關，即ABCDEF無需為凸六邊形），直線AB與DE交于點X，直線CD與FA交于點Z，直線EF與BC交于點Y，則X，Y，Z三點共線．由射影幾何的知識可知，將圓換成任意圓錐曲線，其結論依舊成立.

1.2? 帕斯卡定理的退化形式

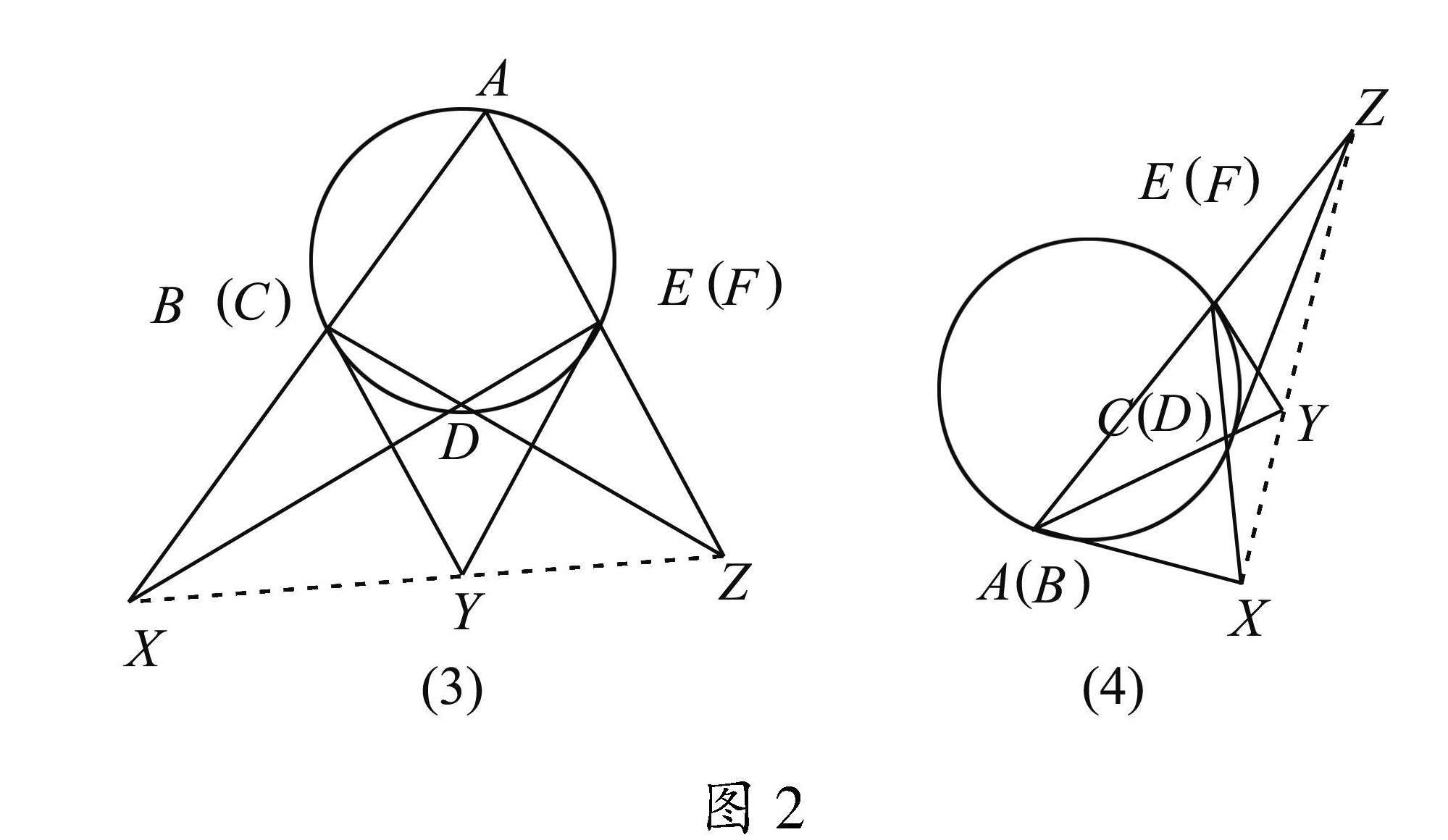
當六邊形中有兩頂點重合，即對于內接于圓錐曲線的五邊形，亦有結論成立.圓錐曲線內接五邊形ABCDEF中A（與B重合）處的切線與DE的交點X，BC與FE的交點Y，CD與AF的交點Z三點共線，如圖2（1）．

圖2

當六邊形變?yōu)樗倪呅蜛BCDEF或ABCDEF等時，如圖2（2），（3），結論仍成立．當六邊形變?yōu)槿切蜛BCDEF時，三組邊AB，CD，EF變?yōu)辄c，如圖2（4），

仍有結論成立．此時三點所共的線也稱為萊莫恩線.

1.3? 帕斯卡定理的特殊情況

我們將兩條平行線認為交于無窮遠處，則有以下結論：

①若圓錐曲線的內接六邊形有且只有一組對邊平行，則另外兩組對邊交點連線與平行對邊平行.②若圓錐曲線的內接六邊形有兩組對邊平行，則第三組對邊也平行［2］.

1.4? 帕斯卡逆定理

帕斯卡逆定理也成立.即如圖1，設ABCDEF內接于圓（與頂點次序無關，即ABCDEF無需為凸六邊形），直線AB與DE交于點X，直線EF與BC交于點Y，若直線CD與XY交于點Z，則點Z在直線FA上.

顯然，帕斯卡定理中同時涉及到圓錐曲線中的點、直線、曲線等基本元素和斜率、定點、定線等基本表征.同時，對斜率、定點、定線的計算或證明又是解析幾何的常見設問方式.因此，帕斯卡定理不失為圓錐曲線命題的一個良好背景.但考慮到圖形的復雜程度、計算的繁雜性、解題的切入口等問題，以帕斯卡定理為背景的題目很少出現在公開的資料中.筆者從不同角度，原創(chuàng)、收集整理了一些相關問題，并對命題背景進行了探索.

直接使用圓錐曲線上的一個任意六點型，常規(guī)計算方法幾乎是無法完成的.因此六點中的某些點需具有一定的特殊性，如簡化橫坐標或縱坐標，或者讓坐標具有某種形式的對稱性.使用左右或上下端點，或者使用一組關于原點對稱的點，是常見的命題手段.

2? 六點型

例1? 已知雙曲線Γ：x225-y216=1與x軸的左右交點分別為B，C.A，P為雙曲線上不與B，C重合的不同兩點，過P做雙曲線Γ漸近線方向的平行線，分別交AB，AC于E，F，求證：EF過定點.

分析? 如圖3，由雙曲線漸近線的性質，假設EP，FP交雙曲線于無窮遠處，交點分別記為S+∞，R+∞.由帕斯卡定理，AB∩PS+∞=E，AC∩PR+∞=F，則BR+∞∩CS+∞=T，且E，F，T三點共線.即過點B，C作漸近線方向的平行線BR，CS.顯然它們交于定點T（0，4）.本題為一個雙曲線中六點型的帕斯卡定理.除了選取左右頂點外，還選取了兩個無窮遠處的點.其常規(guī)解法如下：圖3

由題可知，B（-5，0），C（5，0），由雙曲線的參數方程，設A51+t211-t21，8t11-t21，P51+t221-t22，8t21-t22，則lAB：y=45t1（x+5），lEP：y-8t21-t22=-45x-51+t221-t22，聯立解得E5t1t2-5t1+5t2+5（1+t1）（1-t2），8t1（1+t1）（1-t2）.又lAC：y=45t1（x-5），lFP：y-8t21-t22=45x-51+t221-t22，聯立解得F5t1t2-5t1+5t2+5（1-t1）（1+t2），8t2（1-t1）（1+t2）.故kEF=yE-yFxE-xF=4t1t2+4t1+4t2-45t1t2-5t1+5t2+5，則lEF：y-8t1（1+t1）（1-t2）=4t1t2+4t1+4t2-45t1t2-5t1+5t2+5·x-5t1t2-5t1+5t2+5（1+t1）（1-t2）.由對稱性易知，定點在y軸上，令x=0得，y=-4t1t2+4t1+4t2-45t1t2-5t1+5t2+5·5t1t2-5t1+5t2+5（1+t1）（1-t2）+8t1（1+t1）（1-t2）=-4t1t2+4t1-4t2+4（1+t1）（1-t2）=4，故定點為（0，4）.

3? 五點型

更近一步的，讓其中某兩個點重合，把圖形退化為一個五點型，以使得常規(guī)手段可以計算.

例2? （2023年北京卷）橢圓E：x2a2+y2b2=1（a>b>0），離心率e=53，點A，C分別為E的上下頂點，點B，D分別為E的左右頂點，|AC|=4.

（1）求橢圓E的解析式；

（2）點P為第一象限內橢圓上的一個動點，直線PD與BC交于點M，直線PA與直線y=-2交于點N.求證：MN∥CD.

解? （1）x29+y24=1；

圖4

（2）如圖4，本題選用了上下左右四個頂點.記lCC表示點C處的切線，即直線y=-2.對橢圓的內接六邊形APDCCB，有AP∩lCC=N，PD∩BC=M，CD∩AB=T+∞（T+∞表示兩條平行直線交于無窮遠處）.由帕斯卡定理得M，N，T+∞三點共線，進而MN∥CD.

利用帕斯卡定理1.3的特殊情況，本題設問變?yōu)榱俗C明兩直線平行.而在常規(guī)計算中，平行的轉化手段為斜率或者向量.其常規(guī)解法為：

設P（m，n），點P在橢圓上，則4m2+9n2=36.又D（3，0），則lPD：y=nm-3（x-3）.由B（-3，0），C（0，-2）得：lBC：y=-23x-2.聯立兩直線解得M3（-2m+3n+6）3n+2m-6，-12n3n+2m-6.又A（0，2），則lAP：y=n-2mx+2，與y=-2聯立得N4m2-n，-2.故kMN=-12n3n+2m-6+23（-2m+3n+6）3n+2m-6-4m2-n=6n2-4mn+8m-24-9n2-8m2-6mn+12m+36.將4m2=36-9n2代入可得，kMN=23.又kCD=23，故MN∥CD.

例3? 已知橢圓C：x2a2+y2b2=1（a>b>0）的離心率為23，且7，103為C上的一點.

（1）求C的標準方程；

（2）點A，B分別為C的左、右頂點，M，N為C上異于A，B的兩點，直線MN不與坐標軸平行且不過坐標原點O，點M關于原點O的對稱點為M′，若直線AM′與直線BN相交于點P，直線OP與直線MN相交于點Q.證明：點Q在定直線上.

解? （1）x29+y25=1；

圖5（2）如圖5，AB∩MM′=O，AM′∩BN=P，

O，P，Q三點共線，由帕斯卡逆定理可知，點Q為直線MN與lAA（橢圓在點A處的切線）的交點，即Q在直線lAA：x=-3上.本題是一個定線問題，結合帕斯卡逆定理，將其中四個點設置為左右端點和一組對稱點，將定線設置為左端點的切線，使得本題常規(guī)計算變成可能.常規(guī)解答如下：

由題可知A（-3，0），B（3，0），設M（x1，y1），N（x2，y2），則M′（-x1，-y1）.設lMN：x=my+n，聯立x=my+n，x29+y25=1，消去x得，5m2+9y2+10mny+5n2-9=0，y1+y2=-10mn5m2+9，y1y2=5（n2-9）5m2+9.又易得，lAM′：y=y1x1-3（x+3），lBN：y=y2x2-3（x-3）.由點P為直線AM′和BN的交點得，x1-3y1·yP=xP+3，x2-3y2·yP=xP-3，兩式相加可得，2xP=x1-3y1+x2-3y2yP.化簡得，xP=3mn+3yP，故lOP：x=3mn+3y.由圖像的對稱性知lOP與lMN的交點在一條垂直于x軸的直線上，聯立lOP與lMN得，x=3mn+3y，x=my+n，消去y得，xQ=-3.因此點Q在定直線x=-3上.

4? 四點型

讓其中的兩組點重合，就可將問題轉化為四點型帕斯卡定理.

例4? 橢圓C：x2a2+y2b2=1（a>b>0）的離心率e=32，a+b=3.

（1）求橢圓C的方程；

（2）如圖6，A，B，D是橢圓C的頂點，P是橢圓C上除頂點外的第一象限內一點，直線DP交x軸于點N，直線AD交BP于點M.求證：直線MN過定點.

解? （1）x24+y2=1；

圖6

（2）如圖6，AD∩BP=M，AB∩DP=N，lDD∩lBB=T，由帕斯卡定理，點T在直線MN上.本題選用上頂點和左頂點，使得切線交點容易被找到.其常規(guī)解法為先設出lBP：y=k（x-2），聯立lBP與橢圓，計算出P8k2-21+4k2，-4k1+4k2，進而得lDP：y=-2k+12（2k-1）x+1，N2（2k-1）2k+1，0.聯立lBP與lAD得到M4k+22k-1，4k2k-1.利用M，N兩點坐標得出lMN：y=2k+14x-2（2k-1）2k+1，進而得到定點T（2，1）（此處具體解答過程從略）.

5? 三點型

例5? 已知O為坐標原點，拋物線Γ：x2=4y上不同的兩點A（4，4），Bb，b24（b≠0）.過A，B兩點做Γ的切線交BO，AO于點M，N.直線MN交x軸于點T（t，0）.當∠AOB為鈍角時，求實數t的取值范圍.圖7

解? 如圖7，顯然x軸為拋物線在點O處的切線，lAA∩BO=M，lBB∩AO=N，M，N，T三點共線，由帕斯卡逆定理知：lOO∩AB=T.顯然，當b∈（-4，0）時，∠AOB為鈍角.對應的，t∈（-∞，0）.本題中，直線MN為△ABO的萊莫恩線.其常規(guī)解法如下：

由y=x24得y′=12x，故kAM=2，進而lAM：y=2x-4.又lOB：y=b4x.聯立lAM與lOB得，y=2x-4，y=b4x，x=168-b，y=4b8-b，即M168-b，4b8-b.同理，lBN：y=b2x-b24，lOA：y=x.聯立lBN與lOA得，y=b2x-b24，y=x，x=b22b-4，y=b22b-4，即Nb22b-4，b22b-4.故TM=168-b-t，4b8-b，TN=b22b-4-t，b22b-4.由TM∥TN得，168-b-t·b22b-4=b22b-4-t·4b8-b，化簡得，t=4bb+4=4-16b+4.又當b∈（-4，0）時，∠AOB為鈍角.故t∈（-∞，0）.

通過上述例證不難發(fā)現，以帕斯卡定理為背景的圓錐曲線問題，立足點、直線、圓錐曲線、平行等基礎知識，充分調度直曲相交、韋達定理、切線求解等基本技能，突出對邏輯推理和數學運算等核心素養(yǎng)的考查.題設豐富，蘊含了圓錐曲線中最常見的定點、定值、定線、范圍、證明等問題.兼顧技巧，如例1中通過觀察圖象的對稱性使得定點簡化，例3中通過合理求解規(guī)避非對稱韋達等.在高考強調“反套路、反機械刷題，突出強調對基礎知識和基本概念的深入理解和靈活掌握，注重考查學科知識的綜合應用能力，落實中國高考評價體系中‘四翼的考查要求”［1］的今天，帕斯卡定理是一座亟待開發(fā)的寶庫.

參考文獻

［1］? 教育部教育考試院.深入考查基礎知識和能力? 助力人才選拔和“雙減”落地：2023年高考數學全國卷試題評析［J］.中國考試，2023（07）：15-21.

［2］? 羅碎海，羅家平，麻紅雷.帕斯卡定理的初等證明與高考題［J］.中學數學研究，2023（07）：17-20.

作者簡介? 唐宜鐘（1988—），男，陜西漢中人，中學一級教師；主要從事高中數學教學和競賽培訓工作.

楚豪（1996—），男，陜西漢中人，中學二級教師；主要從事高中數學教學和競賽培訓工作.