7道原創(chuàng)高考數(shù)學新定義模擬題

基金項目? 北京市教育學會“十三五”教育科研滾動立項課題“數(shù)學文化與高考研究”（FT2017GD003）.

【摘? 要】? 從教育部考試院于2024年1月組織的適應(yīng)性考試反映的信息來看，新定義題將在數(shù)學高考試題中以重要角色出現(xiàn)：情景新穎、思維強度大、創(chuàng)新性強、分值高，甚至可能會以全卷壓軸題的形式出現(xiàn).文章首次發(fā)表的7道原創(chuàng)高考數(shù)學新定義模擬題就是深入領(lǐng)會高考改革方向，做好高三教學和復(fù)習備考的舉措.

【關(guān)鍵詞】? 原創(chuàng)；高考；改革方向；數(shù)學；新定義；模擬題

2024年，吉林等6省及廣西壯族自治區(qū)首次實施“3+1+2”新高考模式，1月19—21日由教育部考試院組織適應(yīng)性考試，語文、數(shù)學、英語三科由教育部統(tǒng)一命題.這次測試，數(shù)學試題（下簡稱測試卷）的改革力度最大，主要包括下面四點：

（1）題量全面減少：由現(xiàn)行的22道左右減少到19道（較以前的多選題、填空題、解答題各減少了一道）.

（2）試題情境創(chuàng)新：比如復(fù)數(shù)題以往多是放在選填題中靠前的位置，但在測試卷放到了選擇題第10題，特別是改變了以往復(fù)數(shù)問題的考查方法.

（3）思維強度增加：尤其是第19題（整個測試卷壓軸題），這道新定義題情境新穎，思維強度提高.全部解答過程沒有繁雜的數(shù)值計算，著重于對新定義的理解，利用新符號的推理過程，通過設(shè)問展現(xiàn)思維過程，考查推理能力.

（4）難度結(jié)構(gòu)調(diào)整：以往的高考試題會設(shè)置三、四個坡度的難度，但測試卷基本上是一個坡度的難度，即所有的單選題、多選題、填空題的難度都比較平緩，只在解答題中設(shè)置了兩道難度大的題目，體現(xiàn)了區(qū)分和選拔的功能.

測試卷的命題風格、試卷布局、難度結(jié)構(gòu)代表了高考改革的方向，將在2024年及以后的新高考中全面體現(xiàn).在中學（包括初中與高中）教學和復(fù)習中應(yīng)高度關(guān)注［1］.

為了切實有效地提高高三復(fù)習備考質(zhì)量，筆者編擬了7道原創(chuàng)高考數(shù)學新定義模擬題（它們均是首次發(fā)表），供有需要的讀者選用.

北京高考數(shù)學卷從2002年開始自主命題，其鮮明特色就是新定義題居多，在選擇題、填空題、解答題的壓軸題中體現(xiàn)得最為明顯.實際上，在高中數(shù)學的各個知識板塊、各種考試題型（還包括數(shù)學文化試題［2］、劣構(gòu)試題等）中均出現(xiàn)了大量的新定義題.

這次編擬的7道模擬題題目文字量大、信息量多、設(shè)問數(shù)量多、情境復(fù)雜、背景深刻（2006年高考福建卷理科第12題及2014年高考福建卷文科第12題、2010年高考廣東卷理科第21題這三道新定義題的背景都是方格幾何學［3］.方格幾何學是由生于俄國的著名德籍數(shù)學家閔可夫斯基（Hermann Minkowski，1864—1909）最先開始研究的）；這7道模擬題的解答難度較大且復(fù)雜（為了突出試題的研究性及其完整性、創(chuàng)新性，會出現(xiàn)一題多解、設(shè)問數(shù)量較多的情形），為了避免解答冗長，可能會在題末給出解答時可使用的參考結(jié)論.為了使讀者深入理解這些題目的科學性與嚴謹性，還會標注相應(yīng)的參考文獻.

這7道原創(chuàng)高考數(shù)學新定義模擬題的最大特點是研究性，所以其中大部分題目并不適合直接放到當前的數(shù)學試卷中使用（主要原因是解答時需要大量時間，而現(xiàn)在的高考時間是極為有限的2h），但可以先把每道題拆分成幾道題（可先選擇原題多個設(shè)問中的部分作為待求解的問題，再在題設(shè)中選擇與待求解的問題相關(guān)的題設(shè)，這樣就得到了一道簡單些的新題），再選擇其中的某道題作為考試題.另外，把這些新定義模擬題作為考試題時，所有的參考文獻均可刪去并且刪去后不會影響考生理解題意和作答.

題1? 公歷又稱陽歷，就是我們平常所說的公元某年某月某日.公歷一年的時間是地球繞太陽公轉(zhuǎn)一周所需要的時間，大約是365.242 198 78天，合365天5時48分46秒.為了使一年的時間是整數(shù)天，就規(guī)定平年365天，閏年366天.公元年份能被4整除的是閏年，但世紀年（指能100整除的年份）要能被400整除的才是閏年，其余的年份均是平年.每年包括12個月，從前到后依次是1月，2月，……，12月，其中1，3，5，7，8，10，12月均月大，每月31天；4，6，9，11月均月小，每月30天；平年的2月28天，閏年的2月29天.

由以上平年及閏年的設(shè)置方法可知，任意連續(xù)的400年中共設(shè)置了97個閏年，共365×400+97=146 097天，平均每年為365.2425天，比實際的一年僅長約0.0003天，需積三千多年才多出一天.

農(nóng)歷又稱陰歷，是根據(jù)朔望月（即月球繞地球旋轉(zhuǎn)一周的時間，大約為29.5306天）安排大月（30天）和小月（29天），力求使農(nóng)歷的平均每個月的時間近似等于朔望月，又根據(jù)公歷一年相當?shù)乃吠聰?shù)安排農(nóng)歷的平年和閏年：平年12個月，閏年13個月.農(nóng)歷既保證了每個月初一是朔（看不見月亮），十五是望（月圓），又保證了農(nóng)歷一年的平均時間近似等于公歷一年的時間.

農(nóng)歷平年的時間為29.5306×12=354.3672天，即354天或355天；農(nóng)歷閏年的時間為29.5306×13=383.8978天，即383天或384天.因為公歷一年為365天或366天，所以公歷的一年比農(nóng)歷的平年多10—12天，比農(nóng)歷的閏年少17—19天.

在我國的二十四節(jié)氣（春雨驚春清谷天，夏滿芒夏暑相連，秋處露秋寒霜降，冬雪雪冬小大寒）中，單數(shù)的叫節(jié)氣，雙數(shù)的叫中氣，并按中氣的順序確定月序，如第一個中氣是雨水，則有雨水的月就是正月，第二個中氣是春分，則有春分的月就是二月.二十四節(jié)氣的公歷日期是比較穩(wěn)定的，如雨水是2月18—20日，春分是3月20—22日，夏至是6月21—22日等等［4］.

明白了以上兩種歷法，再來推算春節(jié)（即農(nóng)歷正月初一）的公歷日期范圍就不難了.

上面已經(jīng)談到，有雨水的月是正月，但雨水在正月的哪一天是不固定的，雨水可以是正月中的任意一天.所以公歷最早的春節(jié)是月日，公歷最晚的春節(jié)是月日.

解? 1，20；2，20.解答過程見文［4］.

題2? 設(shè)m（m≥2）是已知的正整數(shù)，數(shù)列an的項數(shù)至少是m+1.若數(shù)列an的任意連續(xù)m項之和都是常數(shù)D，則稱這個數(shù)列為m-等和數(shù)列，常數(shù)D為這個m-等和數(shù)列的公和，并把2-等和數(shù)列簡稱等和數(shù)列；若數(shù)列an的任意連續(xù)m項之積都是常數(shù)J，則稱這個數(shù)列為m-等積數(shù)列，常數(shù)J為這個m-等積數(shù)列的公積，并把2-等積數(shù)列簡稱等積數(shù)列.給出下列四個結(jié)論：

①常數(shù)列是等和數(shù)列，也是等積數(shù)列；

②等和數(shù)列與等積數(shù)列均是最小正周期為1或2的周期數(shù)列；

③若無窮數(shù)列an是等和數(shù)列，則an=12［D+（D-2a1）（-1）n］（n∈N*）；

④若無窮數(shù)列an是等和數(shù)列，則an=12［D+（2a1-D）cosnπ］（n∈N*）;

⑤項數(shù)與公和均是2024且各項均是自然數(shù)的等和數(shù)列共有2024個；

⑥公積是2024且各項均是自然數(shù)的等積數(shù)列共有16個；

⑦公和是2024且各項均是自然數(shù)的10-等和數(shù)列共有C102034個；

⑧公積是2024且各項均是正偶數(shù)的3-等積數(shù)列共有6個.

其中所有正確結(jié)論的序號是.

簡解? ①③⑥.⑧錯誤：若數(shù)列an是3-等積數(shù)列且公積是2024，則可得an是以3為一個周期的周期數(shù)列.

設(shè)ai=2bi（bi∈N*;i=1，2，3），可得公積a1a2a3=23b1b2b3=2024，所以b1b2b3=1·11·23（b1，b2，b3∈N*）.可得該方程解的組數(shù)是9（其中恰有兩個未知數(shù)取1的解的組數(shù)是3，恰有一個未知數(shù)取1的解的組數(shù)是3！=6），所以公積是2024且各項均是正偶數(shù)的3-等積數(shù)列共有9個.

題3? 人口問題是當今世界各國普遍關(guān)注的問題.認識人口數(shù)量的變化規(guī)律，可以為制定一系列相關(guān)政策提供依據(jù).早在1798年，英國經(jīng)濟學家馬爾薩斯（T.R.Malthus，1766—1834）就提出了自然狀態(tài)下的人口增長模型y=y0ert，其中t表示人口增長經(jīng)過的時間（單位：年），y0表示起初即t=0時的人口數(shù)，r表示人口的年平均增長率，y表示人口增長t年后的人口數(shù)．

（1）由國家統(tǒng)計局網(wǎng)站公布的數(shù)據(jù)知，我國1950年末、1959年末的人口總數(shù)分別為55 196萬和67 207萬.根據(jù)這些數(shù)據(jù)，用馬爾薩斯人口增長模型建立我國在1950—1959年期間的具體人口增長模型（答案中的數(shù)據(jù)要求保留六位小數(shù)）.

（2）利用（1）中的模型計算1951—1958年各年末的人口總數(shù).查閱國家統(tǒng)計局網(wǎng)站公布的我國在1951—1958年間各年末的實際人口總數(shù)，檢驗所得模型與實際人口數(shù)據(jù)是否相符（計算人口數(shù)時答案保留到萬人，說出檢驗思路即可）.

（3）以（1）中的模型作預(yù)測，大約在什么時候我國人口總數(shù)達到13億（答案精確到1年）？

（4）事實上，我國1990年末的人口數(shù)為11.43億，直到2005年才突破13億.對由函數(shù)模型所得的結(jié)果與實際情況不符，你有何看法？

附參考數(shù)據(jù)：

我國在1951—1958年期間各年末的實際人口總數(shù)如表1：

67 207÷55 196=1.217 606…，55 196÷67 207=0.821 283…，ln1.217 606=0.196 886…，

ln0.821 283=-0.196 886…，130 000÷55 196=2.355 243…，55 196÷130 000=0.424 584…，

ln2.355 243=0.856 643…，ln0.424 584=-0.856 643…，0.856 643÷0.021 876=39.159 076…，

130 000÷39.159 076=3319.792 326…，39.159 076÷13=3.012 236….

解? （1）記1950年末為t=0時的情形，則1959年末是t=9時的情形，由題設(shè)可得y0=55 196，67 207=55 196e9r.

由所給的參考數(shù)據(jù)，可解得r≈0.021 876.

因而我國在1950—1959年期間的具體人口增長模型是函數(shù)y=55 196e0.021 876t（0≤t≤9），其中t表示人口增長經(jīng)過的時間（單位：年），y表示人口增長t年后的人口數(shù).

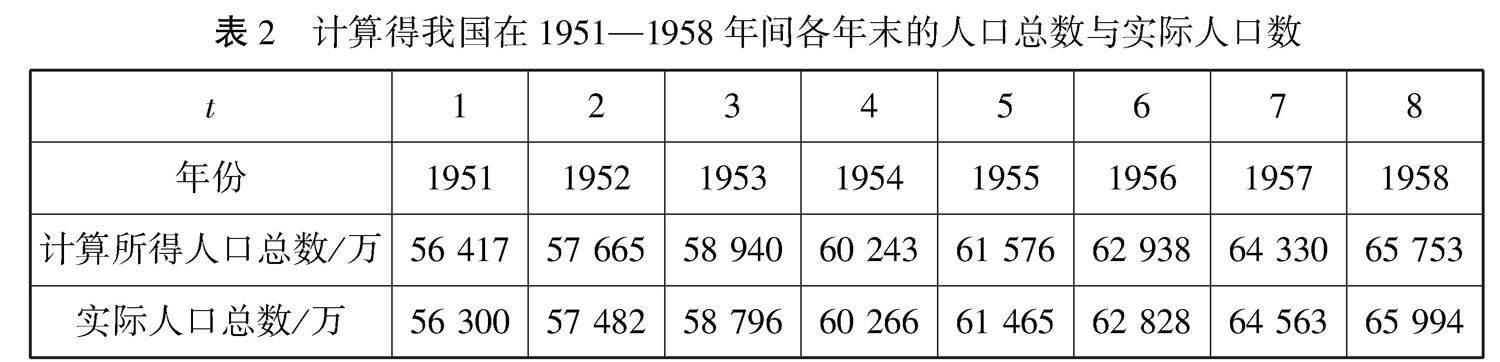
（2）用第（1）問得到的函數(shù)解析式及函數(shù)計算器可計算出我國在1951—1958年間各年末的人口總數(shù)，得到表2：

計算所得人口總數(shù)/萬56 41757 66558 94060 24361 57662 93864 33065 753實際人口總數(shù)/萬56 30057 48258 79660 26661 46562 82864 56365 994

如圖1所示，在平面直角坐標系tOy中作出1950—1959年各年末計算所得人口總數(shù)的散點圖，再作出函數(shù)y=55 196e0.021 876t（0≤t≤9）的圖象：

圖1

若散點圖中的點基本上都在所作的函數(shù)圖象上，則所得模型與實際人口數(shù)據(jù)相符；否則，所得模型與實際人口數(shù)據(jù)不相符.（注：實際的結(jié)果是相符.）

（3）設(shè)從1950年末經(jīng)過x年我國人口總數(shù)達到13億，由（1）中的模型可得

130 000=55 196e0.021 876x，

由所給的參考數(shù)據(jù)，可解得x≈39.159 076.

由進一法取近似數(shù)可知，大約經(jīng)過40年即在1990年我國人口總數(shù)達到13億.

（4）因為我國人口基數(shù)較大，人口增長過快，與我國經(jīng)濟發(fā)展水平產(chǎn)生了較大矛盾，所以我國從20世紀70年代逐步實施了計劃生育政策.因此這一階段的人口增長條件不符合馬爾薩斯人口增長模型的條件，自然就出現(xiàn)了依模型得到的結(jié)果與實際不符的情況.

題4? （1）已知函數(shù)f（x）=b2a2x2-b2（x≥a）及直線l：y=bax，其中a，b是已知的正數(shù).設(shè)函數(shù)f（x）圖象G上的動點M（t，f（t））（t≥a）到直線l的距離是g（t），求證：

（i）圖象G在直線l的下方；

（ii）用減函數(shù)的定義證明g（t）是減函數(shù)；

（iii）ε>0，存在常數(shù)α≥a，使得當t>α時，g（t）<ε.

（2）如圖2所示，當曲線Γ上的動點M沿著曲線Γ無限遠移時，若動點M到某直線l的距離無限趨近于0，則稱直線l是曲線Γ的一條漸近線［5］.

圖2

求證：直線y=bax是曲線y=b2a2x2-b2（x≥a>0，b>0）的漸近線.

鑒于篇幅，過程略，請讀者自解.

注? （1）本題是由平面解析幾何中的結(jié)論“雙曲線x2a2-y2b2=1有且僅有兩條漸近線，且這兩條漸近線的方程分別是y=bax與y=-bax”編擬的一道函數(shù)原創(chuàng)題，該題及其解法對雙曲線漸近線的教學也有指導意義.讀者還容易給出本題第（1）問的三角換元證法.

（2）本題第（2）問結(jié)論的證明不能僅由直觀感知得到，須“從浪漫到精確再到綜合”，因而其本質(zhì)就是證明第（1）問的諸結(jié)論.

（3）讀者還可思考：如何證明“除y=bax外的直線均不是曲線Γ：y=b2a2x2-b2（x≥a）的漸近線”？

題5? 把集合1，2，…，n的所有k（k≤n;k，n∈N*）元子集a1，a2，…，ak的全部元素乘積之和記作∑1≤ai≤na1a2…ak（其中i=1，2，…，k;a1，a2，…，ak兩兩不等，下同），在不發(fā)生混淆時也可簡記為∑a1a2…ak.和式∑1≤ai≤na1a2…ak有如下性質(zhì)：當2≤k≤n;k，n∈N*時，

∑1≤ai≤na1a2…ak=∑1≤ai≤n-1a1a2…ak+n∑1≤ai≤n-1a1a2…ak-1.

再把和式∑1≤ai≤na1a2…ak記作Gkn（k=1，2，…，n;k，n∈N*），又補充定義G0n=1（n∈N*）.

（1）用記號Gkn表示∏ni=1（x+i）即（x+1）（x+2）…（x+n）（n∈N*）的展開式；

（2）寫出Gkn的類似于二項展開式系數(shù)性質(zhì)Cm+1n+1=Cmn+Cm+1n的性質(zhì)并給予證明；

（3）寫出Gkn的類似于楊輝三角的Gkn三角（只寫出前五行）；

（4）求證：若n≥2，n∈N*，則n是質(zhì)數(shù)的充要條件是nGn-1n+1（指Gn-1n+1是n的倍數(shù)）.

解答本題時可使用參考結(jié)論：（威爾遜（Wilson）質(zhì)數(shù)定理［6］）p是質(zhì)數(shù)p（p-1）！+1.

過程略，請讀者自解.

題6? 對于直線l上兩兩互異的三個點A，B，P，若該直線上異于點P的另一點Q滿足PAPB=QAQB（由本題末的參考結(jié)論可知，點Q由三點A，B，P唯一確定），則四點A，B，P，Q叫做一組調(diào)和點列.

設(shè)兩個互異的動點A，B均在定曲線C：x2a2+y2b2=1上，定點P（x0，y0）（x0+y0≠0，x02a2+y02b2≠1）在動直線AB上.已知四點A，B，P，Q是一組調(diào)和點列.

（1）求證：動點Q在某條定直線上；

（2）求動點Q的軌跡方程.

參考結(jié)論：設(shè)兩兩互異的四個定點A，B，M，P（其中M是線段AB的中點）均在定直線l上，則在直線l上存在唯一的異于點P，M的點Q使得PAPB=QAQB，且：

（1）當點P在線段AB的反向延長線上運動時，點Q的軌跡是線段AM（但不是端點）；

（2）當點P在線段AM（但不是端點）上運動時，點Q的軌跡是線段AB的反向延長線；

（3）當點P在線段MB（但不是端點）上運動時，點Q的軌跡是線段AB的延長線；

（4）當點P在線段AB的延長線上運動時，點Q的軌跡是線段MB（但不是端點）.

解題過程略.

注? 在射影幾何中，把（1）中的定直線叫做定點P關(guān)于定曲線C的極線.很多平面解析幾何試題都有極點與極線背景［7］［8］.

題7? 在平面直角坐標系xOy中，到兩個定點F1（-1，0），F(xiàn)2（1，0）的距離的積是定值a2（a>0）的點的軌跡叫做卡西尼（Cassini）卵形線［9］，記作曲線Υa，并把e=1a叫做曲線Υa的離心率，兩個定點F1，F(xiàn)2分別叫做曲線Υa的左焦點、右焦點.

（1）求曲線Υa上的點到坐標原點O的距離的取值范圍；

（2）對于離心率e>1的曲線Υa：

（i）分別求出該曲線上動點的橫坐標、縱坐標的取值范圍；

（ii）求證：0

（3）對于離心率e≤22的曲線Υa：

（i）分別求出該曲線上動點的橫坐標、縱坐標的取值范圍；

（ii）求證：a≥2且該曲線圍成圖形的面積大于a4-1π.

解答本題時可使用參考結(jié)論：長軸長、短軸長分別為u，v的橢圓面積是uvπ.

簡解? 可先求得動點P的軌跡方程是y2=4x2+a4-x2-1（1-a2≤x2≤1+a2），進而可得答案：

（1）a2-1，a2+1；

（2）（i）1-a2，1+a2，0，a44；（ii）略；

（3）（i）-a2+1，a2+1，-a2-1，a2-1；（ii）略.

注? （1）如圖3所示，卡西尼卵形線Υa的形狀共包括下面的四種情形［9］：

圖3

（i）當0

（ii）當a=1時，Υa成8字形自相交叉，稱為“8字形”或雙紐線；

（iii）當1

（iv）當a≥2時，Υa是一條沒有自交點的光滑曲線但曲線中部凸起（當a越大時，中部凸起的越厲害），稱為“類橢圓”.

（2）若P是曲線Υa上的動點（其兩個焦點分別是F1，F(xiàn)2）但不在x軸上，則△F1PF2面積的取值范圍是0，12a2.

可得△F1PF2的面積S△F1PF2=12PF1·PF2sin∠F1PF2≤12PF1·PF2=12a2.由圖3可知，當點P的縱坐標→0（此種情形存在）時，S△F1PF2→0；當點P是以線段F1F2為直徑的圓與曲線Υa的交點（可得兩者交點的個數(shù)是4）時，S△F1PF2=12a2.因而欲證結(jié)論成立.

（3）下面這道高考題的背景就是卡西尼卵形線［9］：

（2011年高考北京卷理科第14題）曲線C是平面內(nèi)與兩個定點F1（-1，0）和F2（1，0）的距離的積等于常數(shù)a2（a>1）的點的軌跡，給出下列三個結(jié)論：

①曲線C過坐標原點；

②曲線C關(guān)于坐標原點對稱；

③若點P在曲線C上，則△F1PF2的面積不大于12a2.

其中，所有正確結(jié)論的序號是．（答案：②③.）

參考文獻

［1］? 本刊編輯部.數(shù)學科高考最重大最全面的改革［J］.中學數(shù)學教學參考（上旬），2024（02）：1.

［2］? 甘志國.介紹一道原創(chuàng)“數(shù)學文化”高考模擬題［J］.中學數(shù)學雜志，2018（03）：48-49.

［3］? 甘志國.有趣的方格幾何［J］.新高考（高二·數(shù)學），2013（11）：39-40.

［4］? 甘志國.春節(jié)的公歷日期［J］.數(shù)理天地（高中版），2008（11）：46.

［5］? 劉玉璉，傅沛仁.數(shù)學分析講義（上冊）［M］.2版.北京：人民教育出版社，1981：258-262.

［6］? 魏萬迪.整數(shù)入門［M］.成都：四川教育出版社，1988.

［7］? 甘志國.二次曲線的兩條性質(zhì)及其應(yīng)用［J］.中學數(shù)學雜志，2024（01）：33-38.

［8］? 甘志國.對2020年高考數(shù)學北京卷第20題與第21題的思考［J］.高中數(shù)理化，2020（13-14）：19-21.

［9］? 甘志國.高中數(shù)學題典：平面解析幾何［M］.哈爾濱：哈爾濱工業(yè)大學出版社，2016：533.

作者簡介? 甘志國（1971—），男，湖北竹溪人，研究生學歷，正高級教師、特級教師、湖北名師、政府專項津貼專家、北京民進名師專家團專家、甘志國特級教師工作室主持人；2018年7月2日，北京市豐臺區(qū)教委召開了“北京市特級教師甘志國教育科研研討會”；對高考數(shù)學試題及重點高校強基計劃數(shù)學試題研究深入；鉆研教法與學法，提倡并關(guān)注學生運算能力的培養(yǎng)；總結(jié)提出并踐行“懂、會、熟、巧、通”五步解題學習法，“思、探、練、變、提”五步解題教學法，“知、懂、熟、用、賞”五種解題境界及高中數(shù)學教學的四個關(guān)鍵詞“夯實基礎(chǔ)、激發(fā)興趣、著眼高考、適當提高”；倡導教師要做明師——明白的教師；已發(fā)表文章多篇（2016-2023年均發(fā)表了北京高考數(shù)學試題綜述文章），已出版獨著61冊（總計31 326千字，其中27冊署名“甘志國著”）.