基于GA-RBF網絡的混合氣體紅外光譜定量檢測

摘? 要：混合氣體組分的定量分析在各個領域都尤為重要，傳統的氣體成分檢測方法一般是采用電化學法和氣相色譜法，此類方法檢測效率低下、精度不夠，且無法做到實時測量。為解決這一問題，本文由HITRAN光譜數據庫獲取100組混合氣體樣本數據集，以樣本中CO2和H2O組分為例，利用RBF網絡分別進行定量識別。結果得知，兩種氣體在訓練集和測試集的預測濃度值與實際濃度值偏差均較大， RBF網絡無法準確的預測出混合氣體組分的濃度。為改進該問題，考慮到模型參數對RBF網絡回歸預測精度的影響，本文在此基礎上提出一種GA優化RBF網絡的混合氣體組分濃度檢測方法。通過引入GA優化RBF網絡模型參數，獲取最優參數組，再將優化模型用于混合氣體組分定量識別。并與RBF網絡預測算法在同一數據集上對比論證，探討模型改進效果。實驗結果表明，相較于單獨使用RBF網絡，改進后的GA-RBF模型在混合氣體組分定量識別問題中，表現更為優異。

關鍵詞： 紅外光譜；RBF神經網絡；遺傳算法；濃度檢測

1 概述

混合氣體組分濃度檢測一直是研究熱點，它在各大領域都發揮著重要作用，如機動車尾氣排放、工業廢氣污染排放檢測等。隨著我國經濟的快速增長，人們在對生活品質關注的同時也對生存環境提出了更高的要求，因工業廢氣、汽車尾氣等有毒氣體的排放造成了嚴重的環境污染。尤其是在垃圾焚燒行業，尾氣中含大量CO2、H2O等氣體，煙氣濕度高達70%，且監測的氣體組分復雜，以往投入火電廠[1]使用的常溫儀表在使用過程中由于尾氣的特性極易造成腐蝕問題，后期維護量大，系統使用壽命短暫。因此提出一種能夠準確檢測混合氣體組分濃度的方法具有較大價值。

基于紅外光譜技術的混合氣體濃度檢測問題是紅外光譜領域的重要問題。隨著計算機技術的飛速發展，利用機器學習算法與紅外光譜技術相融合[2]用于混合氣體組分濃度檢測逐漸成為研究熱點。大數據時代的開啟，使得從繁雜的數據庫中高效提取出有用數據成為可能。這些新技術和理論促進了我國原有檢測技術的發展，同時大幅度提高了檢測精度。

傳統氣體檢測方法會受到外界環境，如溫度、壓強等因素的影響，所測準確度并不穩定，需與其他方法相結合，才能達到檢測目標。現階段提高傳感器檢測精度的方法主要有人工神經網絡[3] （ANN）法和支持向量機[4] （SVM）等機器學習算法。王瑋[5]用BP網絡檢測出了CO、SO2、NO的單一氣體的濃度，平均誤差達到3.59%。太惠玲等[6]人采用3層BP神經網絡檢測出CO和H2濃度，CO和H2平均相對誤差分別是0.74%和1.75%。Lei Zhang等[7]人對比了SMIMO和MMISO兩種算法在多層感知網絡優化上的應用，得出MMISO在氣體濃度估計上誤差更小。

以上方法對單一氣體的濃度檢測精度較高，但對多組分混合氣體的濃度檢測精度往往達不到要求。本文以此出發，提出一種改進RBF網絡的混合氣體組分定量分析方法。首先通過GA優化RBF網絡模型參數，獲取最優參數組，再將優化模型用于混合氣體組分定量識別。并與傳統RBF網絡預測算法在同一數據集上對比論證。

2 混合氣體濃度檢測的RBF網絡模型

2.1 RBF網絡訓練算法

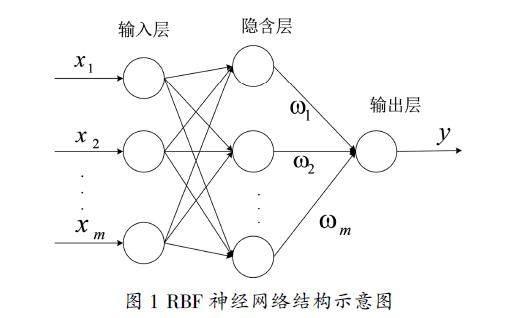
RBF網絡是一種包含三層網絡結構的前向型網絡，網絡結構如圖1所示[8]。

RBF網絡基本思想是：用徑向基函數作為隱單元的“基”，構成隱層空間。隱層對輸入向量進行變換，將低維空間的模式變換到高維空間，使低維空間線性不可分的問題在高維空間內線性可分。

實現步驟如下：

2.1.1 確立徑向基函數中心點

設訓練集樣本輸入矩陣和輸出矩陣分別如下式（2.1）和（2.2）所示：

其中，表示第個訓練樣本的第個輸入變量；表示第個訓練樣本的第個輸出變量；為輸入變量的維；為輸出變量的維；為訓練集樣本總數。

2.1.2 確定隱含層神經元閾值

令個隱含層神經元對應的閾值為式（2.3）

其中，，為徑向基函數的擴展速度。

2.1.3 確定隱含層與輸出層間權值和閾值

當隱含層神經元的徑向基函數中心及閾值確定后，隱含層神經元的輸出便可以

由式（2.4）計算：

其中，為第個訓練樣本向量。并記。

設隱含層和輸出層間的連接權值為式（2.5）

其中，表示第個隱含層神經元與第個輸出層神經元之間的連接權值。

設個輸出層神經元的閾值為下式（2.6）

由RBF神經網絡結構可得式（2.7）

其中

求解線性方程組（2.7），即可得到隱含層和輸出層之間的權值W和閾值b2，如式（2.8）所示

本節所采用的混合氣體光譜數據集由HITRAN光譜數據庫獲得，共100組。將數據集隨機劃分為訓練集和測試集。其中，訓練集包含80組數據，測試集包含20組。

通過上述理論分析，本節將利用RBF神經網絡對包含CO2和 H2O樣本的混合氣體紅外光譜數據集進行訓練和回歸預測，并結合平均相對誤差及預測值與真實值的擬合相關系數作為模型評價指標，對預測結果進行分析。

2.2 兩種氣體濃度預測實驗驗證與分析

2.2.1 RBF網絡對CO2氣體的定量分析

將隨機選擇的80組數據作為訓練集樣本建立回歸分析模型。在測試集上驗證模型的預測效果，訓練集樣本CO2的模型預測濃度值與實際濃度值對比如圖2所示。

由圖2可以看出，利用訓練集樣本建立的RBF模型對訓練集數據做預測時，效果不理想，模型預測濃度值無法較好的擬合真實值。對數據誤差進行計算，結果可得訓練集平均相對誤差為0.237，實際濃度值與預測濃度值的擬合相關系數為0.8067。由兩個模型評價參數可知，RBF網絡對CO2訓練集濃度的預測效果較差。

將訓練后的RBF模型應用于測試集，測試集的實際濃度和預測濃度對比如圖3。

由圖3可以看出，將模型用于測試集的預測，其預測濃度值與實際濃度值偏差同樣比較大。對數據誤差進行計算，測試集平均相對誤差為0.215，實際值與預測值的擬合相關系數為0.7986。

由以上分析可知RBF算法在測試集上的回歸分析能力效果較差，RBF網絡無法準確地預測CO2組分濃度。故此模型不能用于混合氣體中CO2組分濃度的定量分析。

2.2.2 RBF網絡對H2O氣體的定量分析

為使實驗仿真結果更具說服力，在同一混合氣體數據集下，將RBF網絡用于H2O訓練集和測試集樣本的濃度回歸預測，所得實驗結果如下圖4所示。

計算數據誤差，結果可得訓練集平均相對誤差為0.599，相關系數為0.7432。預測濃度與實際濃度偏差較大，預測效果不理想。將訓練的模型應用于測試集，測試集的實際濃度和預測濃度對比如下圖5所示。

圖5 H2O測試集實際濃度和預測濃度對比

根據圖5結果可以得知，將模型用于測試集的預測，其預測濃度值與實際濃度值擬合效果較差。計算數據誤差可知，測試集平均相對誤差為0.431，預測濃度值與真實濃度值擬合相關系數為0.7352。分析可知RBF算法對H2O的回歸預測能力較差，RBF算法無法準確地預測H2O組分濃度。模型不適用于混合氣體中H2O組分濃度的定量分析。

RBF網絡對兩種氣體組分在訓練集和測試集上預測的模型評價參數如下表所示：

由表1 RBF模型預測結果分析可知，RBF神經網絡在混合氣體組分定量識別問題中呈現出的結果并不理想，RBF網絡無法準確預測出混合氣體組分濃度。考慮到RBF網絡模型參數對識別精度的影響。為解決這一問題，本文在RBF網絡的基礎上提出一種改進算法，即遺傳算法（GA）優化RBF網絡的混合氣體組分濃度預測方法。

3 GA優化RBF網絡用于混合氣體組分定量分析

3.1 GA基本原理

遺傳算法（GA）是根據自然界生物體的進化規律而提出的，是一種模擬自然進化過程進而搜索最優解的方法[9]。該算法通過數學求解方式，利用計算機仿真運算，將問題的求解過程轉換成類似生物進化中的染色體基因的選擇、交叉和變異等的過程。通過種群一代代的不斷進化，最終收斂到“最適應環境”的個體，從而求得問題最優解。

遺傳算法（GA）是模型參數優化的常用方法。該算法的基本優化過程是采用基于適應度函數的選擇、交叉和變異等操作，獲取網絡模型的最優參數組，以此來提高網絡的預測精度。論文采用GA對RBF神經網絡的主要參數不斷調節和優化，其中主要參數包括有中心值c、寬度σ和連接權值w等。再以對輸出響應值有影響的若干個特征因子作為輸入神經元，輸出響應值作為輸出神經元，對GA-RBF神經網絡模型進行訓練和測試。并將模型應用在與上述RBF預測算法同一樣本數據集上對比論證，觀察GA-RBF模型的預測效果。

3.2 GA優化RBF實現過程

GA優化RBF網絡具體實現流程如下圖6所示：

從圖6中可以看出遺傳算法優化RBF神經網絡主要包括三個模塊：確定網絡結構、遺傳算法優化模型參數以及RBF網絡預測。首先根據輸入和輸出參數的個數確定基本的網絡結構，確立遺傳算法中個體長度值。再通過比較不同寬度種群下的適應度值及遺傳算子的變異概率，對遺傳操作方式不斷地改進。最后對優化所得最優個體分別賦與RBF神經網絡的初始權值、中心值及閾值，訓練完成后對網絡進行預測分析。

優化的基本要素包括種群初始化、計算適應度函數、選擇、交叉與變異操作。

3.2.1對種群進行初始化

通過GA對種群中的個體進行編碼，編碼后的個體相當于一個實數串，它包括四個部分，分別是輸入層與隱含層的連接權值、隱含層閾值、隱含層與輸出層的連接權值以及輸出層閾值。

3.2.2計算適應度函數

首先依據個體獲取RBF網絡的初始權值及閾值，通過訓練后的RBF網絡在訓練集上預測適應度值，適應度值計算方法如公式（3.1）所示：

上式中，為第個輸出點的預測值，為第個輸出點的期望值，為輸出節點的個數，為系數。

3.2.3選擇操作

依據預測的適應度值大小執行選擇操作，若令個體被選中的概率為，則其計算方法如公式（3.2）所示：

上式中，，為種群個體的適應度值，為種群中所包含的個體數。

3.2.4交叉操作

個體的編碼方式采用的是實數編碼，因此交叉操作采用實數交叉。如第個染色體與第個染色體在位進行交叉操作，則有：

上式中，為[0，1]之間的隨機數。

3.2.5變異操作

以種群個體的第個染色體為例，變異操作可表示為：

上式中，為的上限，為的下限。；是隨機數，是當前的尋優次數，為設定的迭代次數，為[0，1]之間的隨機數。

3.3 優化模型在樣本集中的驗證分析

本節以包含CO2、H2O組分的混合氣體數據集作為研究對象，對兩種氣體單獨建模進行濃度的定量分析。其中，混合氣體中CO2濃度范圍為0.08%～48.83%，H2O濃度范圍為0.03%～39.58%。

選擇與上述RBF預測方法相同的100組混合氣體光譜樣本數據集，其中80組樣本作為訓練集，融合遺傳算法建立神經網絡優化模型，觀察優化模型在訓練集上的回歸預測效果。選取其余20組樣本作為測試集，利用訓練后的模型在測試集上回歸預測，驗證優化模型在測試集上的預測精度。將優化模型預測結果與單獨使用RBF神經網絡對比分析，比較兩者的預測值與真實值擬合相關系數和平均相對誤差，評價兩種模型在混合氣體組分定量分析中的優劣。

建立神經網絡模型需合理優化選取初始權值、中心值及閾值，本節利用GA實現參數尋優過程，其具體步驟如上圖6所示。

具體優化步驟為：

（1） 選取與上述RBF預測相同的100組實驗數據用作樣本集，其中80組為訓練樣本集，其余20組用為測試樣本集。

（2） 確定RBF網絡結構。本節同時對含兩組分的混合氣體定量識別，因此可設置RBF網絡結構為2-7-1模式，即輸入層節點數目為2，隱含層節點數目為7和輸出層節點數目為1。

（3） 初始化網絡獲取初始權值、閾值。

（4） 初始化GA各個參數。本次實驗選擇種群的規模為80；選取空間[10，100]；迭代次數設定為400；交叉概率設定為0.3，設定范圍[0，1]；變異概率取0.1。根據所設參數，初始化種群初始位置及尋優速度。

（5） 設定適應度函數是訓練數據預測誤差的絕對值之和。

（6） 對種群初始化。

（7） 迭代尋優求解出最優初始權值、中心值及閾值。根據式（3.2）、（3.3）與（3.4）對個體執行選擇、交叉與變異操作，通過對個體適應度值的橫向及縱向對比獲取當前最優個體。

（8） 判斷尋優結果是否符合結束條件，若不符合，則跳到第六步繼續執行此過程。

將通過GA優化獲得的最優個體賦與RBF網絡，進而對訓練樣本集訓練并以此構建神經網絡回歸模型，再在此基礎上對測試集驗證分析模型預測結果。

對于兩種氣體分析模型的參數優化過程，設定種群數量80，GA優化迭代次數為400，交叉概率0.3，變異概率0.1。按照圖6的優化流程逐步進行，若以橫軸為迭代次數，縱軸為適應度值，可得到如下圖7所示的GA優化過程中最優個體適應度值變化規律曲線。

3.3.1 GA-RBF對CO2氣體的定量分析

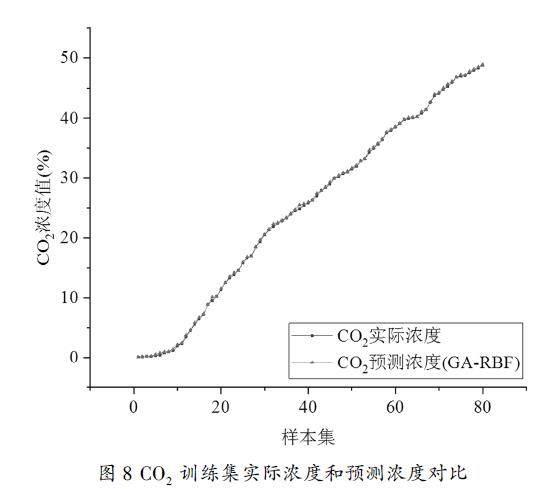
對于篩選出的80組樣本數據，將其作為訓練集樣本訓練，構建優化回歸模型。分別在訓練集和測試集上對模型的回歸效果驗證分析。其中，模型在訓練集樣本上預測濃度值和實際濃度值對比結果如下圖8所示。

由圖8可看出利用訓練樣本集建立的模型對訓練集本身做預測時，預測效果較好，預測濃度值能夠很好的擬合真實濃度值。對數據誤差進行計算，結果可得訓練集平均相對誤差為0.041，預測濃度值與實際值濃度的擬合相關系數為0.9671。分析可知GA-RBF模型相較于單獨使用RBF，具有較好的回歸預測能力，可以準確預測樣本中的CO2濃度。

將訓練后的模型用于測試集驗證，測試集樣本的實際濃度值和預測濃度值對比如下圖9所示。

觀察圖9可知，GA-RBF模型在測試集預測效果較好，其預測濃度值與實際濃度擬合程度較高。可推斷GA-RBF模型可以用于混合氣體組分CO2濃度的定量分析。? ?計算可得測試集平均相對誤差為0.024，預測值與真實值的擬合相關系數為0.9576。分析可知GA-RBF模型相較于單獨使用RBF，具有較好的回歸預測能力，可以精確預測樣本中CO2的濃度信息。

3.3.2 GA-RBF對H2O氣體的定量分析

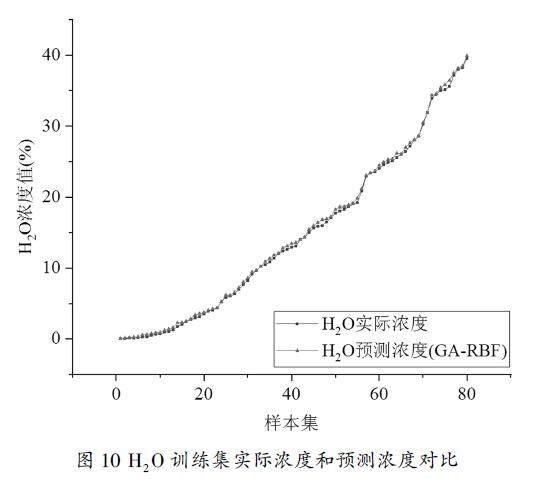
對于隨機選擇的80組樣本數據，將其作為訓練樣本訓練，構建優化回歸分析模型。分別論證模型在訓練集和測試集上的預測效果。訓練集樣本中模型預測濃度值和實際濃度值對比結果如下圖10所示。

圖10 H2O訓練集實際濃度和預測濃度對比

由圖10可看出利用訓練集樣本建立的模型對訓練集本身做預測時效果較好，預測值能夠很好的擬合真實值。對數據誤差進行計算，結果可得訓練集平均相對誤差為0.138，相關系數為0.9482。分析可知GA-RBF模型相較于單獨使用RBF而言，具有更好的回歸預測能力，可以較為準確地預測樣本中的H2O濃度信息。

將訓練好的模型應用于測試集進行驗證，測試集樣本實際濃度值和預測濃度值對比如下圖11所示。

圖11 H2O測試集實際濃度和預測濃度對比

觀察圖11可知，GA-RBF模型的預測效果較好，將GA-RBF模型用于測試集的預測，其預測濃度值與實際濃度值能夠較好的擬合，由此可推斷GA-RBF模型可以用于混合氣體中H2O濃度的定量分析。對數據誤差進行計算，結果可得測試集平均相對誤差為0.084，相關系數為0.9436。可知GA-RBF模型相比于單獨使用RBF而言，具備較好的回歸分析能力，可以較為準確地預測出H2O樣本濃度信息。

GA-RBF算法在兩氣體組分訓練集和測試集上預測的模型評價參數如表2所示：

由表2 GA-RBF模型的預測結果評價參數分析可知，其在混合氣體組分定量識別問題中表現優異，模型優化效果較好。

4 結論

本文首先選取RBF神經網絡算法用于混合氣體組分濃度預測，將由HITRAN光譜數據庫獲取的100組混合氣體樣本數據集，隨機分為訓練集和測試集，其中訓練集包含80組數據，測試集包含20組數據。經預處理輸入至RBF神經網絡模型，以混合氣體組分CO2和H2O為研究對象，利用RBF網絡模型分別對兩種氣體組分進行定量識別。由預測結果分析可知，RBF模型對兩種氣體組分的濃度預測精度均比較低，模型預測結果無法滿足要求。因此為改進RBF網絡對混合氣體組分預測效果差的問題，考慮到模型參數對RBF網絡回歸預測精度的影響，本文在RBF網絡的基礎上提出了一種改進算法，即GA優化RBF網絡用于混合氣體組分濃度預測。通過GA優化RBF網絡模型參數，獲取最優參數組，再將優化后的模型用于混合氣體組分定量識別。為排除實驗隨機性，選擇與RBF網絡預測算法相同的樣本數據集上對比論證。實驗結果表明，相較于單獨使用RBF算法，GA-RBF優化模型在混合氣體組分的定量識別問題中，表現更加優異。

參考文獻：

[1]Ayslan S. P. Costa， Josefa M. S. Gon?alves， Hosana O. et al. Application of Near-Infrared for Online Monitoring of Heavy Fuel Oil at Thermoelectric Power Plants. Part I： Development of Chemometric Models[J]. Industrial & Engineering Chemistry Research，2019，58（34）：550-558.

[2]El Khoury Youssef， Gebelin Marie， de Sèze Jér?me， et al. Rapid Discrimination of Neuromyelitis Optica Spectrum Disorder and Multiple Sclerosis Using Machine Learning on Infrared Spectra of Sera[J]. International Journal of Molecular Sciences， 2022，23（5）：672-679

[3]張志峰. 基于直接吸收光譜的高濃度氣體檢測研究及甲烷氣體檢測樣機開發[D]. 濟南：山東大學，2022.

[4]翁靜， 袁盼， 王銘赫， 等. 基于支持向量機的泄漏氣體云團熱成像檢測方法[J]. 光學學報， 2022， 42（09）：104-111.

[5]王瑋. 基于氣體傳感器陣列的混合氣體檢測系統[D]. 西安：西北工業大學，2002.

[6]太惠玲， 謝光忠， 蔣亞東. 基于氣體傳感器陣列的混合氣體定量分析[J].儀器儀表學報， 2006（07）：666-670.

[7]Lei Zhang 0038， Fengchun Tian. Performance Study of Multilayer Perceptrons in a Low-Cost Electronic Nose.[J]. IEEE Trans. Instrumentation and Measurement， 2014，63（7）：1670-1679.

[8]Ziteng Wen， Linbo Xie， Hongwei Feng， et al. Robust fusion algorithm based on RBF neural network with TS fuzzy model and its application to infrared flame detection problem[J]. Applied Soft Computing Journal， 2019，76：782-789.

[9]Duan Wenyang， Zhang Peixin， Huang Limin， et al. Ship hull surface reconstruction from scattered points cloud using an RBF neural network mapping technology[J]. Computers and Structures， 2023，281：209-215.

作者簡介：吳廣譜（1996—? ），男，漢族，安徽宿州人，碩士（在讀），學生，研究方向：紅外光譜、混合氣體成分識別與濃度檢測。