一種基于金融時間序列數據的深度學習風險預測方法

朱林

摘要：金融時間序列數據的指標按照不同的會計準則會得到不同的數值，如何取舍會受到人為因素的干預。針對金融時序數據的領域泛化專門提出一種異常檢測方法，解決特征分布的多樣性和復雜性，捕捉金融序列數據的特有表征模式。將循環神經網絡之后獲得的結果僅作為學習到的知識，通過標準分類器在特征空間對其邊緣分布進行適配，然后再通過隱變量自回歸模型進一步進行預測，以此來提高預測的精度。然后，構建一個隱變量自回歸模型來進行風險預測，通過捕捉金融時間序列數據之間的特征分布來識別其中的金融風險，實驗結果表明，模型具有一定的可行性。

關鍵詞：深度學習；金融時間序列數據；特征分布；金融風險；異常檢測

一、前言

深度學習已經被廣泛應用于計算機視覺和自然語言處理領域。但是與圖像領域和自然語言處理領域有較多的經典網絡結構可選擇不同，金融時間序列數據處理吸引了大批研究者探索其未來研究的方向。嘗試使用深度學習技術增強金融風險防范措施，無論在基礎理論研究上還是對于國民經濟和社會發展中的金融風險防范工作，都具有很高的研究和應用價值。

二、深度學習技術在金融風險預測領域的作用

異常檢測是一門由來已久的技術，已經廣泛應用于各個領域。隨著近些年深度學習技術的突飛猛進，兩項技術的集合受到了諸多研究者的關注，并且也在一些領域展開了應用，網絡入侵檢測[1]、智慧醫療[2]、傳感器網絡[3]，以及視頻異常檢測[4]等。一個金融時間序列數據的指標按照不同的會計準則會得到不同的數值，如何取舍會受到人為因素的干預。當前被判定合規的數據標簽，在金融風險真實發生后再回溯人工智能的學習過程，相當于非主觀有意地對模型數據進行“投毒”。有研究者注意到，深度學習模型，無論卷積神經網絡還是循環神經網絡提取到的特征都具有相似性和繼承性[5]，嘗試將其應用在其他具備一定特征的金融時序數據集上進行泛化研究，對于探索深度學習在金融風險預測工作上的有效性具有應用意義。與其他很多異常檢測場景不同，在實務中，金融風險不一定意味著損失，也可能是套利的機會。在金融時間序列數據場景下獲得準確的標簽的代價是十分昂貴的，尤其是異常數據在一開始往往會標記成正常數據，因為事件之初，總有各種各樣的解釋背書該操作的合理合規性。如何通過多源時序數據的時空關聯性來發現通用表征模式，不同的是這里誤導模型的將不再有噪聲數據，而是并不太準確，事后往往被發現錯誤標注的標簽數據。這是金融時序數據場景下異常檢測面臨的另一個關鍵挑戰。

本文提出一種針對金融時序數據的領域泛化異常檢測方法，解決特征分布的多樣性和復雜性，捕捉金融序列數據的特有表征模式。該方法基于循環神經網絡，但在架構上分為兩個學習模塊。在兩個學習模塊之間具有學習到的特征知識的傳遞，先在一個源領域上進行pre-train，使用循環神經網絡作特征提取模塊，然后在目標領域上進行隱變量的自回歸分析（latent autoregressive models）。

三、研究方案

（一）將數據的學習和使用分為兩個部分

在該模型中，金融時間序列數據領域所有的標簽被認為都只有在事后才能明確其準確性。那么，該模型的設計方案中在循環神經網絡之后獲得的結果僅把它當做學習到的知識，通過標準分類器在特征空間對其邊緣分布進行適配，然后再通過隱變量自回歸模型進一步進行預測，通過這樣的方法來提高預測的精度。

（二）使用隱變量自回歸模型尋找金融風險的分布特征

該研究使用隱變量自回歸模型計算預測值與標簽之間的分布距離，對于特征空間進行分布適配。雖然大多數深度研究的前提都是滿足獨立同分布這一要求，金融時間序列數據相較于其他數據集在這一點上矛盾并不突出，但也不能認為在嚴格意義上完全符合。假設在其他時間序列中的噪音，在該領域指不由各種機構有意操控的數據分布下的金融時間序列數據。在更多考慮金融時間序列數據的時間依賴性、空間依賴性，以及金融“噪音”數據分布的各種影響后，通過當前的方案使得正常數據在隱變量特征空間具有獨立同分布這一特性，在沒有添加生成數據的同時可以提高研究模型的魯棒性。

四、方案設計

（一）復合深度學習框架

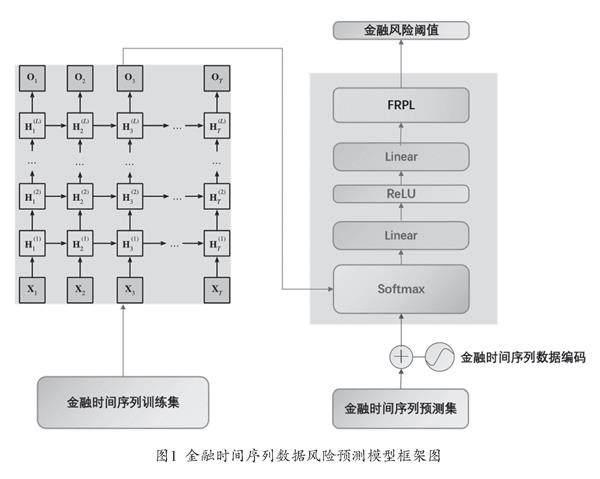
本研究中對深度學習各種模型的層次架構進行操作，建立一個可以互相銜接使用的數據處理學習機制架構。構建由循環神經網絡與隱變量自回歸模型組合的復合架構如圖1所示，旨在通過隱變量的特征學習，將過去時間金融數據以及其在隱變量自回歸模型中預測產生的誤差，再進行統一的學習。

在金融時間序列數據中，每個金融機構包含m個指標、n個（n>1）金融機構的數據集，定義S表示指標集合，模型所獲得的金融時間序列數據總體有N=|S|=mn個指標，每一個指標為xi∈S，xi∈Rti×1。其中，ti表示指標xi的長度。目標限定在金融時間序列數據這一種時間序列上，完成對于金融風險的預測這一學習任務。利用相似性度量在大量金融數據集進行學習，通過學習找出金融數據時間序列計算風險閾值的較優方法。

假設當前某一機構的時間序列數據為Xi，那么向下一個隱變量自回歸模型傳遞的特征知識由循環神經網絡進行計算，如公式（1）。

（1）

其中，Ht-1是上一個時間點的該機構金融時間序列數據計算獲得的特征知識，即X=（x1…，xN）T∈RN×T表示包含所有數據源的輸入樣本。

通過本研究的方式，尋找相鄰時間隱變量Ht和Ht-1之間的關系，并將學習到的信息保留在當前時間的隱變量之中。這些隱變量在模型的下一個計算層，將被送入帶有激活函數的全連接層。隨后使用隱變量自回歸算法來做金融時間序列數據集異常特征的線性預測，將不同機構的特征帶入當前學習的特征中去進行隱變量自回歸分析。利用特征空間中的數據分布信息來探測當前數據源的特征是否異常。按照既定的研究目標將循環神經網絡在指定金融時間序列數據集內學習到的特征知識表示作為隱變量自回歸模型的輸入。

對于金融時間序列數據集中的標簽與模型預測值之間的距離，當前研究使用交叉熵來進行計算。為了考慮一個機構的金融時間序列數據集在前后時間線上的預測差距規模，使用時間累積影響度這個值來衡量整個序列中所有時間預測值之間的交叉熵損失，如公式（2）。

（2）

前置循環神經網絡計算金融時間序列數據的訓練數據，學習獲得符合獨立同分布要求的隱變量知識，再通過隱變量自回歸模型學習獲得金融時間序列數據集在相關機構、相關時間上的預測差距規模，如公式（3）。

（3）

λ為模型目標函數的超參數，用于調整誤差之間的權重大小。LCEL 為前置循環神經網絡的訓練誤差，該值指示了學習到的隱變量知識是否能夠很好地保留輸入樣本的特征分布，這里誤差計算使用交叉熵。LMSE表示隱變量自回歸模型的訓練誤差，通過這個值考查正常情況與異常情況之間的距離，以探測金融風險。

最終通過深度學習獲得的是一個風險閾值，它在不同金融場景下意義可能不同。對于金融機構，它可以是止盈止損閾值。對于監管機構，它可以是管控紅線。這里的訓練集X={x1，x2，…，xD}，xi∈RN×T是包含風險存在的、真實的一個時間段內的特征集合。FRPL（xi）是對應樣本標簽xi在循環神經網絡結合隱變量自回歸模型訓練之后得到的距離總和，u是其均值。η是超參數，通過這種模型的不斷應用形成這個超參數的特征標簽庫之后，η也可以通過深度模型學習獲得，如公式（4）。

（4）

在預測階段，通過判斷是否預測樣本特征xi的距離FRPL（xi）>FRthreshold，如果大于，則該樣本xi被標定為金融風險，反之為正常。

五、實驗結果分析

（一）該模型與僅使用循環神經網絡之間的比較

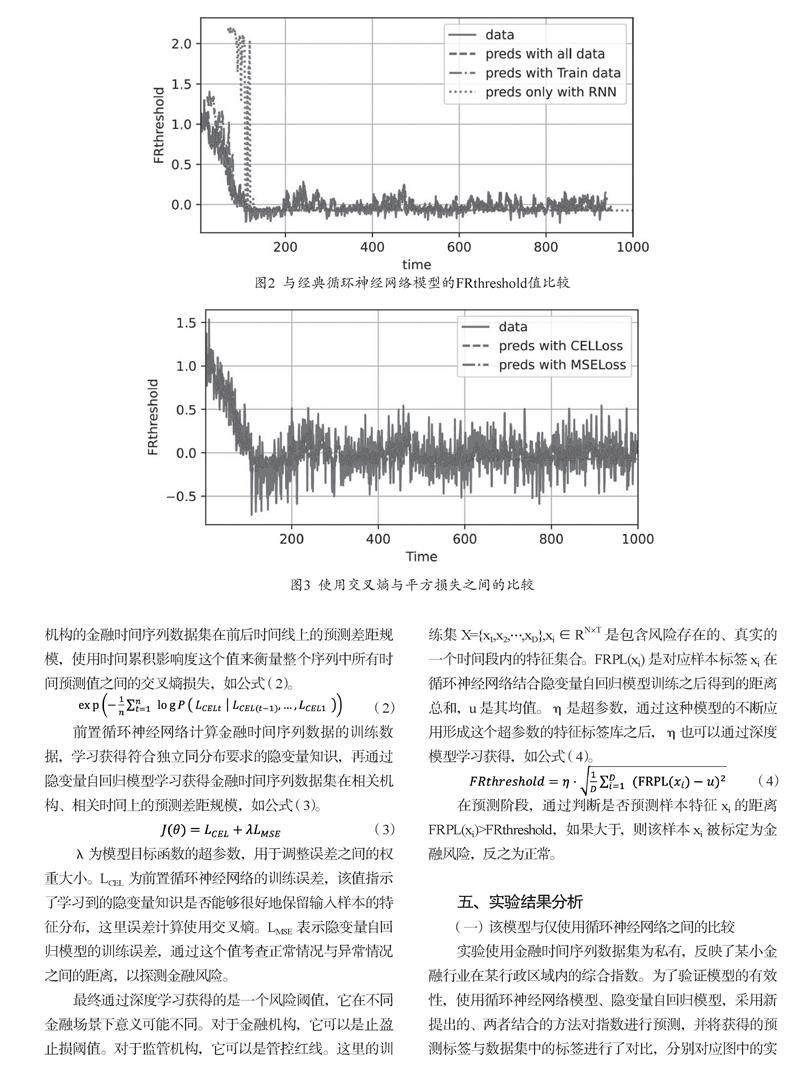
實驗使用金融時間序列數據集為私有，反映了某小金融行業在某行政區域內的綜合指數。為了驗證模型的有效性，使用循環神經網絡模型、隱變量自回歸模型，采用新提出的、兩者結合的方法對指數進行預測，并將獲得的預測標簽與數據集中的標簽進行了對比，分別對應圖中的實線段和點化線線段，如圖2所示。可以看出在短期內該模型有預測能力，長期預測情況下，能力會被不斷削弱，但也要強于全點線所對應的循環神經網絡。

如果將預測測試集的數據也投入訓練，可以得到圖2中的虛線線段曲線，對于監管場景下的應用具有實踐價值。

（二）該模型使用交叉熵與平方損失之間的比較

協變量漂移將會導致誤差的積累，在數據脫離金融規律的循環之后，預測將不再準確，甚至會因為在模型內部達到某個奇點而造成自動梯度下降的算法失靈。即使來自于同一個行業，由于協方差漂移問題的存在，在源域特征分布與目標域特征分布之間也存在差異。該研究相較于異常檢測中常規使用的LMSE，來度量這兩個分布之間的差距，使用了交叉熵來處理這種距離損失。通過實驗結果數據可以看出該模型取得了一個更好的效果，如圖3所示。

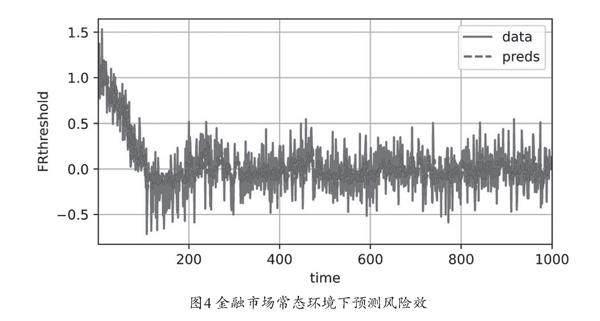
（三）金融市場常態環境下預測風險效果

如果給定的金融時間序列數據完全剔除金融市場中的黑天鵝事件、灰犀牛事件，該模型可以獲得比較滿意的結果，如圖4所示。在應用于金融時間序列數據的特征分布比較穩定的情景下，該模型可以預測出該市場金融風險閾值的發展趨勢。由于在金融時間序列中，正常和異常數據往往具有同一個類別的標簽，考慮到其數據分布的差異性，實際上在不同階段可以給這些數據集賦予新的偽標簽。

六、結語

本研究具體方法是首先構建循環神經網絡新的隱知識學習體系，然后，構建一個隱變量自回歸模型來進行風險預測。通過捕捉金融時間序列數據之間的特征分布特征來識別其中的金融風險，實驗結果表明，模型具有一定的可行性。

參考文獻

[1] Chalapathy R， Chawla S. Deep learning for anomaly detection： A survey [J]. arXiv preprint arXiv：1901.03407， 2019.

[2] Litjens G， Kooi T， Bejnordi B E， et al. A survey on deep learning in medical image analysis [J]. Medical image analysis， 2017， 42： 60-88.

[3]Ball J E， Anderson D T， Chan C S. Comprehensive survey of deep learning in remote sensing： theories， tools， and challenges for the community [J]. Journal of Applied Remote Sensing， 2017， 11（04）： 042609.

[4]Kiran B， Thomas D， Parakkal R. An overview of deep learning based methods for unsupervised and semi-supervised anomaly detection in videos [J]. Journal of Imaging， 2018， 4（02）： 36.

[5]Zhang Y， Chen Y， Wang J， et al. Unsupervised deep anomaly detection for multi-sensor time-series signals[J]. IEEE Transactions on Knowledge and Data Engineering， 2021， 35（02）： 2118-2132.

基金項目：1.貴州省第六批千層次人才項目（項目編號：筑科合同-GCC[2022]011）；2.2024年度貴州省基礎研究計劃（自然科學類）項目“基于金融數據的時間序列在線深度遷移學習研究”（項目編號：黔科合基礎-ZK[2024]一般520）

作者單位：貴陽學院電子信息工程學院

■ 責任編輯：王穎振、鄭凱津