立足教材 拓展延伸

在初中的概率知識(shí)中，我們主要接觸到的概率模型是“摸球模型”和“幾何概型”，拋硬幣、擲骰子均屬于“摸球模型”。掌握“摸球模型”是學(xué)好概率的基礎(chǔ)，我們先回顧教材上的內(nèi)容。

一、教材分析【源自蘇科版數(shù)學(xué)教材九（上）136頁(yè)—139頁(yè)】

例題 一只不透明的袋子中裝有1個(gè)白球和2個(gè)紅球，這些球除顏色外都相同，攪勻后從中任意摸出1個(gè)球，記錄顏色后放回、攪勻，再?gòu)闹腥我饷?個(gè)球。求兩次都摸到紅球的概率。

練習(xí) 一只不透明的袋子中裝有1個(gè)紅球和1個(gè)白球，這些球除顏色外都相同，攪勻后從中任意摸出1個(gè)球，記錄顏色后放回、攪勻，再?gòu)闹腥我饷?個(gè)球。求兩次摸到的球顏色相同的概率。

習(xí)題 一只不透明的袋子中裝有2個(gè)白球和1個(gè)紅球，這些球除顏色外都相同，攪勻后從中任意摸出1個(gè)球，記錄顏色后放回、攪勻，再?gòu)闹腥我饷?個(gè)球。求兩次都摸到紅球的概率。

【思路分析】例題、練習(xí)、習(xí)題都是“從中任意摸出1個(gè)球，記錄顏色后放回、攪勻，再?gòu)闹腥我饷?個(gè)球”，涉及兩個(gè)因素，可以使用“列表格”或“畫(huà)樹(shù)狀圖”求概率。但要注意例題中的2個(gè)紅球是相互獨(dú)立的，習(xí)題中的2個(gè)白球也是相互獨(dú)立的。

【規(guī)律總結(jié)】當(dāng)一次試驗(yàn)涉及兩個(gè)步驟時(shí)，可以用“列表法”或“畫(huà)樹(shù)狀圖法”不重復(fù)、不遺漏地列出所有等可能的結(jié)果。當(dāng)出現(xiàn)的結(jié)果數(shù)較多時(shí)，通常用列表法；當(dāng)一次試驗(yàn)涉及3個(gè)或3個(gè)以上步驟時(shí)，就只能用樹(shù)狀圖列出所有結(jié)果了。

二、問(wèn)題變式

在一個(gè)不透明的箱子里放有除顏色外其余都相同的3個(gè)小球，其中紅球2個(gè)、白球1個(gè)。

（1）攪勻后，從中隨機(jī)摸出1個(gè)球，然后不放回，再隨機(jī)摸出1個(gè)球，求兩次都摸出紅球的概率。

（2）攪勻后，甲、乙、丙三人依次按順序從中任意摸出1個(gè)球（摸出的球不放回），甲、乙、丙3人摸到白球的概率相同嗎？為什么？

【思路分析】在變式問(wèn)題中，要注意條件的變化對(duì)事件概率的影響。對(duì)于第（1）問(wèn)，當(dāng)摸球后不放回時(shí)，因同一個(gè)球不能被摸到兩次，所以列表時(shí)對(duì)角線(xiàn)上的結(jié)果就不存在了，可用線(xiàn)段劃去：

[ 白 紅1 紅2 白 （白，紅1） （白，紅2） 紅1 （紅1，白） （紅1，紅2） 紅2 （紅2，白） （紅2，紅1） ][果][第二次

摸球][第一次

摸球] [結(jié)]

如果選擇畫(huà)樹(shù)狀圖，則不放回時(shí)，第一步有3個(gè)分叉，而第二步只有2個(gè)分叉：

由表或圖可知，共有6種等可能的結(jié)果，兩次都摸出紅球的結(jié)果有2種，所以?xún)纱味济黾t球的概率為[26]=[13]。

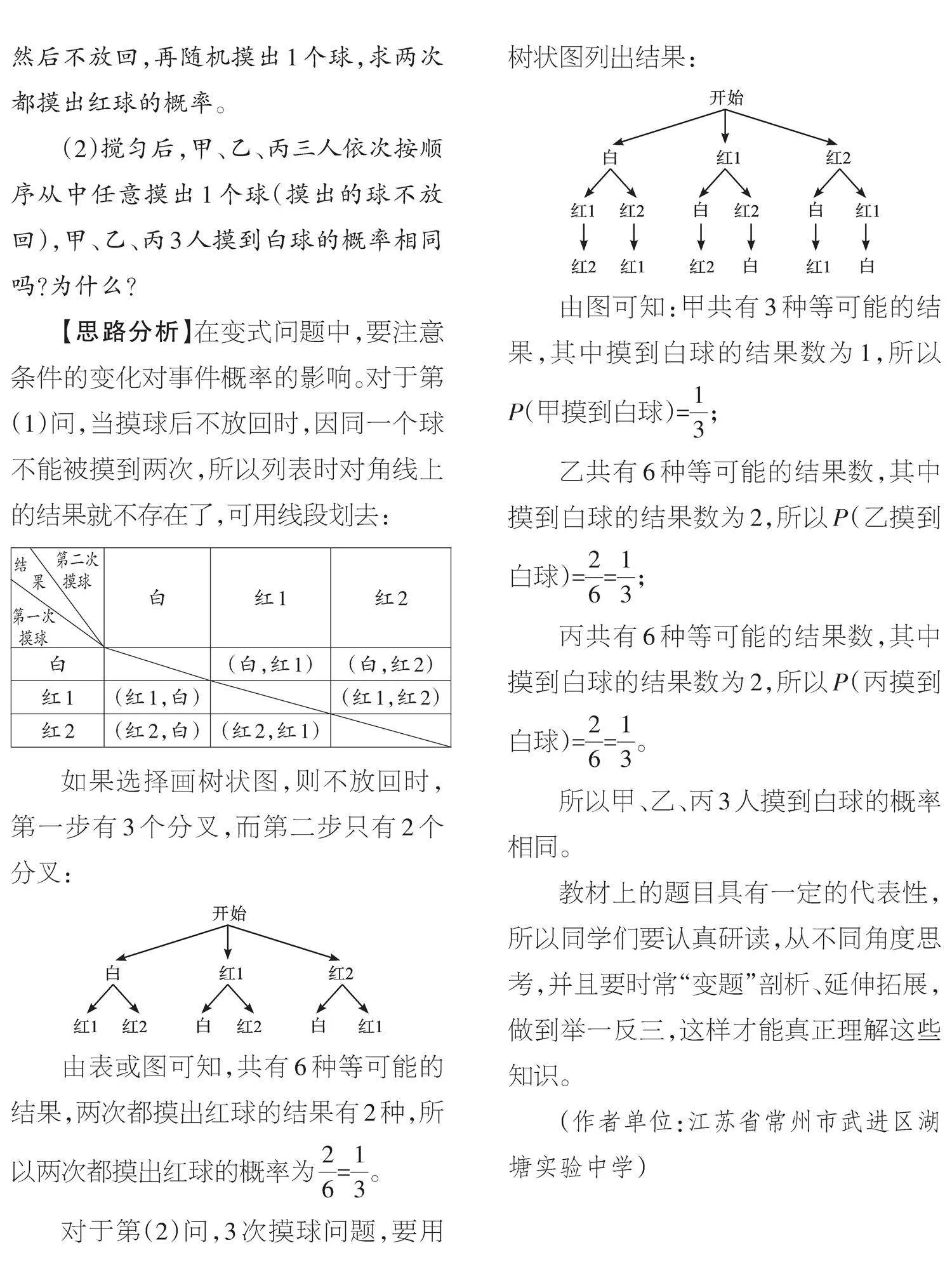
對(duì)于第（2）問(wèn)，3次摸球問(wèn)題，要用樹(shù)狀圖列出結(jié)果：

由圖可知：甲共有3種等可能的結(jié)果，其中摸到白球的結(jié)果數(shù)為1，所以P（甲摸到白球）=[13]；

乙共有6種等可能的結(jié)果數(shù)，其中摸到白球的結(jié)果數(shù)為2，所以P（乙摸到白球）=[26]=[13]；

丙共有6種等可能的結(jié)果數(shù)，其中摸到白球的結(jié)果數(shù)為2，所以P（丙摸到白球）=[26]=[13]。

所以甲、乙、丙3人摸到白球的概率相同。

教材上的題目具有一定的代表性，所以同學(xué)們要認(rèn)真研讀，從不同角度思考，并且要時(shí)常“變題”剖析、延伸拓展，做到舉一反三，這樣才能真正理解這些知識(shí)。

（作者單位：江蘇省常州市武進(jìn)區(qū)湖塘實(shí)驗(yàn)中學(xué)）