基于自適應網格多目標鯨魚算法的火力分配問題研究

摘要： 傳統多目標優化算法在解決多于兩個目標函數的火力分配問題時收斂效果不佳，多樣性差，耗時過大。基于此，提出了一種自適應網格多目標鯨魚優化算法（AG-MOWOA）來解決以震塌比例、彈藥成本和自身剩余價值為目標函數的火力分配問題。該算法引入混沌映射和外部Pareto存檔進化策略提高了種群的多樣性，通過自適應網格選取最優個體的方法極大地減少了算法運行時間。仿真實驗結果表明，該算法較其他算法收斂速度更快、收斂質量更高、解集分布更多樣，能夠有效解決火力分配問題。

關鍵詞： 火力分配； 混沌映射； 自適應網格劃分； 多目標優化； 鯨魚優化算法

中圖分類號： TP301.6;E91

文獻標志碼： A

文章編號： 1671-6841（2024）06-0017-08

DOI： 10.13705/j.issn.1671-6841.2023010

Research on Firepower Assignment Problem Based on Adaptive

Grid Multi-objective Whale Algorithm

SHE  Wei1，2，3， WANG Yeteng1，3， KONG Defeng4， LIU Wei1，2，3， LI Yinghao1，2， TIAN Zhao1，3

（1.School of Cyber Science and Engineering， Zhengzhou University， Zhengzhou 450002， China;

2.Henan Collaborative Innovation Center for Internet Medical and Health Services， Zhengzhou University，

Zhengzhou 450052， China; 3.Zhengzhou Key Laboratory of Blockchain and Data Intelligence，

Zhengzhou 450002， China; 4.Institute of Engineering Protection， National Defense Engineering

Research Institute， The Academy of Military Sciences， Luoyang 471023， China）

Abstract： The traditional multi-objective optimization algorithm had poor convergence effect， bad diversity and serious time-consuming problems when solving the firepower assignment problem with more than two objective functions. Based on this situation， an adaptive grid multi-objective whale optimization algorithm （AG-MOWOA） was proposed. The algorithm was to solve the firepower assignment optimization problem in which the collapse ratio， ammunition cost， and the own surplus value were taken as the objective functions. Besides， the algorithm increased the population diversity by introducing chaotic mapping and using external Pareto archival evolutionary strategy， and reduced the algorithm running time greatly by selecting the optimal individuals through adaptive grid. The results of the simulation experiments showed that the algorithm had better convergence speed and stability， and more diverse solution set distributions than other traditional algorithms in solving the firepower assignment problem.

Key words： firepower assignment; chaotic mapping; adaptive grid generation; multi-objective optimization; whale optimization algorithm

0 引言

隨著現代戰場智能化程度的不斷提高，對于火力籌劃方法的要求也越來越高，傳統的根據某項指標對火力分配方案進行篩選的方法已經無法適應現代戰場中復雜多變的環境，在如今仿真作戰場景下需要更加高效準確的方法來處理大量戰場信息，對敵方目標進行火力分配方案的優選是火力籌劃方法研究中的關鍵問題之一。

關于火力分配方案的選擇已經不單單是基于彈藥對目標最大毀傷效果的篩選，而是有選擇地根據現有資源合理分配，在對敵方造成盡可能大的毀傷效果的情況下使自身損耗盡可能小［1］。文獻［2］以作戰資源消耗最少、近距離作戰武器損失價值最小、敵方戰場剩余價值最小為優化目標構建防御場景下的動態火力分配模型，并利用A-NSGA-GKM算法對模型進行求解，通過仿真實驗證明了算法解決動態火力分配問題的有效性。文獻［3］以實際毀傷與期望毀傷的差值平方和為目標函數構建火力分配模型，利用改進遺傳算法對模型進行求解，在達到預期毀傷要求的基礎上盡可能減少火力資源浪費，有效增加了火力分配方案的靈活性。這些研究均根據不同的作戰場景設計了相適應的優化目標。

火力分配方案的求解是一種多目標優化問題，如何在多個優化目標中尋求一種平衡是多目標優化要解決的主要問題，求解此類問題的本質就在于找到問題模型的Pareto前沿解集［4］。文獻［5］提出一種基于協同進化的混合變量多目標粒子群優化算法，利用協同進化策略提高搜索效率，引入基于結構學習的重組策略提高種群多樣性，解決了無人機協同多任務分配問題。文獻［6］提出了一種改進NSGA-Ⅲ算法，利用連續編碼方式增加初始種群的多樣性，采用隨機選擇，模擬二進制交叉和多項式變異作為種群進化策略，有效解決了集群目標火力分配問題。

上述方法雖然在算法收斂速度與效果上較一些經典算法有所提升，但還是普遍存在難以跳出局部最優解、全局搜索能力差的問題。鯨魚優化算法（whale optimization algorithm， WOA）是一種元啟發式優化算法，在2016年由Mirjalili等首次提出［7］，它通過模仿鯨魚的狩獵行為實現對目標問題的求解，具有控制參數少、可擴展性強、跳出局部最優能力強的特點。在傳統的WOA基礎上，文獻［8］利用多種群探索機制增加種群多樣性、引入二次插值法提高算法收斂速度、通過控制參數設置平衡算法的開發與探索能力。文獻［9］使用柯西逆累積分布函數提高WOA的全局搜索能力，并利用改變權重的方法提高了算法的局部搜索能力和收斂精度。文獻［10］通過非線性種群初始化、增加邊界優化條件和引入精英個體引導機制對WOA改進，有效提高了算法的多樣性與收斂速度。

傳統的單目標算法在求解復雜問題上存在較大的局限性，因此多目標優化算法的設計與研究具有重大的意義，文獻［11］提出了一種非支配排序的WOA，通過非支配排序擁擠度計算策略與狩獵行為對種群非支配解集的迭代更新實現多目標優化。文獻［12］利用反向精英保留策略和種群引導策略加快了算法收斂速度，引入種群引導策略和Levy變異策略，提高了算法的全局搜索能力。上述方法都利用計算個體擁擠度的方式在新組成的種群中挑選最優個體，不但會增加算法的計算量，還會因為種群數量的限制而降低種群的多樣性。

本文針對火力分配提出一種改進的多目標鯨魚優化算法，該方法利用混沌映射初始化種群，進行自適應網格劃分選擇最優個體，進而結合外部Pareto檔案進化種群。仿真實驗表明，本文方法較之同類方法具有更好的搜索能力與收斂性。

1 相關技術

多目標優化算法的重要環節就是尋找解空間中的非支配解集，本節對多目標優化、非支配排序以及鯨魚優化算法進行介紹。

1.1 多目標優化

最小化的多目標優化問題的數學模型表示為

minF（x）=（f1（x），f2（x），…，fm（x）），x∈S，（1）

其中：S為解空間；m為目標函數的個數。多目標優化的目的就是找到x*=

argminx*∈S（f1（x），f2（x），…，fm（x））的解x*。在實際應用中，這些目標函數都是互相矛盾的，即優化一個目標函數的代價是劣化其他目標函數，很難達到一種資源分配的理想狀態，并且這種理想狀態往往都存在多種解［13］，如何在解空間內找到所有這樣的解集是多目標優化算法要解決的主要問題。

1.2 非支配排序

解決多目標優化問題首先要引入Pareto支配關系的概念，對于m個目標函數fi（x），i=1，2，…，m，給定任意兩個決策變量x1和x2，如果滿足式（2）條件，則可稱解x1支配x2，

fi（x1）≤fi（x2）， i∈1，2，…，m，

fi（x1）<fi（x2）， i∈1，2，…，m。（2）

如圖1，設目標函數f1和f2為越小越好，A、B、C、D、E和F為存在于目標空間中的6個解。其中B在兩個目標函數上都要優于E，根據式（2）就可以稱B支配E，同理也可以得出C支配F，而對于A與D，由于解空間中不存在支配它們的解，因此A、B、C、D所在的超曲面就構成了目前解空間中如圖1中曲線所示的Pareto前沿。

因此如果對于一個決策變量來說，沒有其他任何決策變量能夠支配它，那這個決策變量就稱為非支配解。非支配排序就是將所有決策變量中滿足此條件的解放入一個集合中，構成Pareto前沿解集，標記為第一層，之后排除找到的所有非支配解并對剩余個體再次進行非支配排序，得到的Pareto前沿解集標記為第二層，以此類推直至處理完種群中的所有個體［14］。

1.3 鯨魚優化算法

鯨魚優化算法模擬了自然界中鯨魚的捕食過程：鯨魚在發現獵物之后會成群地將獵物圍住，螺旋運動游向目標并在這個過程中不斷吐出氣泡，形成一種柱狀“氣泡網”將獵物緊緊包圍在中心，直至鯨魚靠近一口吞下。鯨魚的捕食策略可以將其看作一個不斷逼近優化問題最優解的過程，其中每頭鯨魚可以看作是優化問題中的一個解，獵物可以看作是需要求得的最優解，因此可以模仿鯨魚的捕食過程來解決優化問題［15］。

1） 環繞獵物

鯨魚是群居動物，只要種群中某個個體發現獵物，則其他個體就會向它移動爭搶獵物。在優化問題中把具有最佳適應度函數的個體視為種群的最優個體，種群中其他個體朝著最優個體變化位置的過程用數學模型表示為

X（t+1）=X*（t）-AD，

D=CX*（t）-X（t），（3）

其中：t為當前的迭代次數;X（t）為當前鯨魚的位置;X*（t）為目前得到的最優鯨魚位置;X（t+1）為更新后的鯨魚位置。A和C為相關系數，如式（4）所示，

A=2aR1-a，C=2R2，a=2（tmax-t）/tmax，（4）

其中：R1和R2為［0，1］上的隨機浮點數；tmax為設定的最大迭代次數；a為收斂因子，會隨著迭代次數的增加逐漸遞減至0。

2） “氣泡網”狩獵

鯨魚在狩獵的過程中會吐出“氣泡網”包圍獵物，因此設計出兩種數學模型來表示這種捕獵行為。

收縮包圍。通過公式（3）不斷收縮接近獵物，與公式（3）不同之處在于A的取值范圍，由于鯨魚在接近獵物的時候才會發出“氣泡網”困住獵物，而A隨著迭代次數的不斷增加會逐漸減小，所以這里設置在A<1時，鯨魚更新后的位置可以是它與最優個體之間任意位置。

螺旋游動。鯨魚會螺旋游向獵物，可以用數學模型表示為

X（t+1）=X*（t）+Dpeblcos（2πl），

Dp=X*（t）-X（t），（5）

其中：Dp代表鯨魚與最優個體之間的距離；b是一個用來定義螺旋形狀的常數，通常取1；l為（-1，1）上的隨機浮點數。

以上介紹的兩種狩獵行為發生在不同鯨魚的捕食過程中，為了更好地模擬行為的異步性，引入行動概率P來決定鯨魚是選擇收縮包圍還是螺旋游動接近獵物，鯨魚個體在生成的隨機數小于P時進行收縮包圍，不小于P時進行螺旋游動，因此鯨魚“氣泡網”狩獵的數學模型為

X（t+1）=

X*（t）-ACX*（t）-X（t）， p<P，

X*（t）+X*（t）-X（t）eblcos（2πl）， p≥P，（6）

其中：p為區間［0，1］上的隨機浮點數；P為行動概率常數，通常設置為0.5。

3） 搜索狩獵

鯨魚還可以在全局搜索獵物，其數學模型表示為

X（t+1）=Xrand（t）-AD，

D=CXrand（t）-X（t），（7）

其中：Xrand（t）為在種群隨機選擇的鯨魚位置，當A≥1時，鯨魚會隨機選擇種群中的個體進行位置的更新，增強算法的全局搜索能力。

2 火力分配問題描述

假設有m種彈藥資源用于打擊n個地面目標，彈藥總資源集合為W=｛w1，w2，…，wm｝，打擊目標集合為T=｛t1，t2，…，tn｝，彈藥成本向量為C=｛c1，c2，…，cm｝，決策變量為彈藥數量集合X=｛x1，x2，…，xm｝。

針對問題描述選定火力分配的目標函數為以下3個。

1） MTxT8Grxns+81l1zsWDPyPv/k93dpRKASKTtoe/ztgM=震塌比例。在目標毀傷效果選取方面，目前大多數的相關研究均通過設定毀傷概率來模擬某彈藥打擊某目標［16］，此類方法雖然能夠一定程度上反映火力分配過程中彈藥對目標的毀傷效果，但是存在較大的主觀性與隨機性，并不能真實反映具體種類彈藥對于具體種類目標的毀傷效果。因此本文以有限元仿真獲得的彈藥對特定目標的毀傷效應數據，在提高毀傷效果真實程度的同時，縮短仿真時間。

ye=Ansys（x1，x2，…，xm），（8）

其中：Ansys表示有限元仿真的過程；x1，x2，…，xm表示輸入的m種彈藥種類。

2） 彈藥成本。彈藥資源的消耗量也是火力分配方案優劣性評估的重要指標，表示為

yc=∑mi=1cixi。（9）

3） 自身剩余價值。考慮在實際作戰中敵方作戰單元遭受火力打擊后的反擊行為和我方作戰單元作戰后對自身價值的消耗，這里將敵我雙方的對抗性行為和自身價值的消耗用自身剩余價值來描述，

yt=∑mi=1cixi（1-hiε（xi）），（10）

其中：hi為武器打擊目標后自身的損傷概率；ε（xi）為階躍函數。

綜上所述，本文提出的火力分配問題可以描述為

max（ye），

min（yc），

max（yt），（11）

s.t. minBdi≤xi≤maxBdi，xi∈N，i=1，2，…，m，（12）

其中：式（11）為火力分配問題的優化目標;式（12）為約束條件;maxBdi和minBdi分別為彈藥數量的上、下界。

3 改進的多目標鯨魚優化算法

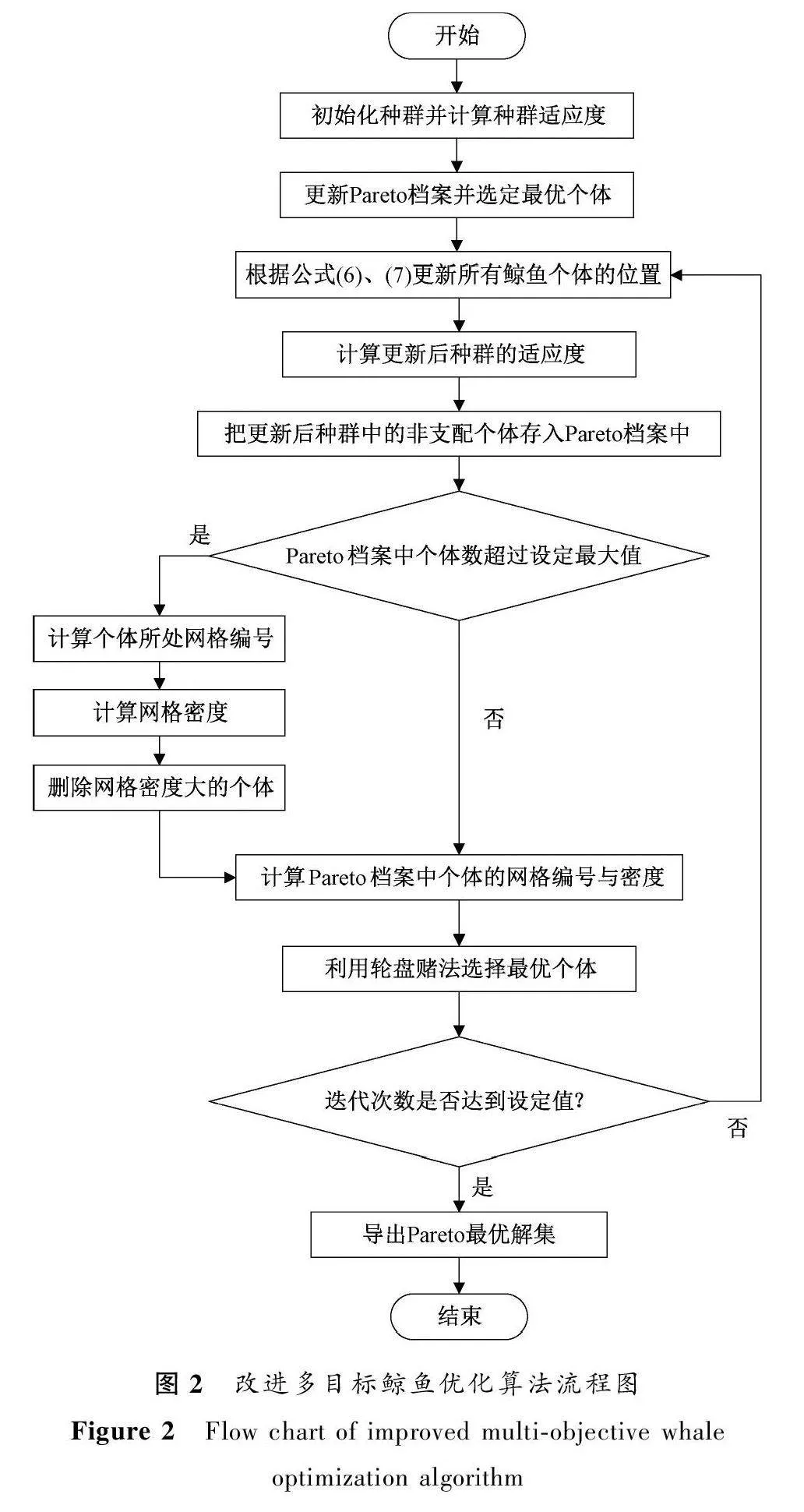
對所提出的改進的自適應網格多目標鯨魚優化算法（adaptive grid multi-objective WOA，AG-MOWOA）進行介紹，包括種群初始化、最優個體選擇、Pareto存檔進化等過程。算法流程如圖2所示。

3.1 種群初始化

采用混沌映射的方法來進行種群的初始化，Logistic方程是一個典型的混沌映射系統［17］，

Zn+1=μZn（1-Zn），n=0，1，2，…，（13）

其中：Z為［0，1］上的隨機浮點數;μ被稱為Logistic控制參量，是［0，4］上的隨機浮點數，研究表明μ在（3.567，4］時整個混沌系統會呈現出一種偽隨機分布的狀態，且在靠近4時可以通過迭代不重復地經歷空間中所有位置。所以用這種方法來初始化種群可以極大地提高初始種群在解的空間內的分布質量，具體操作步驟如下。

1） 初始化一個規模為m的種群，在［0，1］內生成隨機解向量z0=（z0，1，z0，2，…，z0，m）。

2） 利用Logistic方程進行迭代產生混沌序列。

3） 將得到的混沌序列映射到輸入解空間中，

Zi，j=zi，j（Cmax-Cmin）+Cmin，

Zi=（Zi，1，Zi，2，…，Zi，m），（14）

其中：Zi為混沌序列向量zi對應的輸入解空間向量;Cmax和Cmin分別為輸入解空間的最大與最小值向量。

4） 假設種群大小為N，計算所有輸入解空間向量的目標函數，并根據非支配關系選出其中最優的N個個體作為初始種群。

3.2 最優個體選擇

傳統的單目標鯨魚優化算法可以根據適應函數值的大小選擇最優個體，但是擁有多個目標函數的種群往往有多個最優個體，以什么樣的標準來選取領導鯨魚群更新位置是設計多目標鯨魚優化算法的重要問題之一。

目前大多數多目標優化算法都是通過計算個體間的擁擠度來實現非支配解集優劣的排序，但是這個計算過程比較復雜且不利于算法的全局搜索，因此本文選用基于自適應網格劃分［18］的方法來選擇最優個體。

網格密度可以用來描述目標空間中每個區域所包含的個體數量，區域內的個體越多，網格密度就越大；個體越少，網格密度就越小。為了維持種群個體的多樣性，網格密度越小的區域內的個體越有機會被選為最優個體。以目標函數一為例，關于網格信息計算方法的數學模型為

M=［Grid×yi（t）-minY（t）maxY（t）-minY（y）］，（15）

其中：M代表個體所處的網格編號；［·］表示括號內數值向下取整;取小于括號內數的最大整數；

Grid為網格要劃分的網格數；t為迭代次數；yi（t）為第t代個體i的目標函數值；maxY（t）為第t代種群所有個體中對應目標函數的最大值；minY（t）為第t代種群所有個體中對應目標函數的最小值。

此時通過式（15）得到所有個體的網格編號元組，利用輪盤賭法選擇最優個體，處于同一個編號組的個體越多，該網格的密度就越大，選中這個網格中個體作為最優個體的概率就越小。當選中的網格有多個個體時，隨機選擇其中一個個體作為最優個體。

3.3 Pareto存檔進化

在目前許多群智能算法的研究中都會引入Pareto外部檔案用來存儲種群迭代過程中產生的非支配解，當外部檔案中的個體超過提前設定好的值之后，就需要根據相應的策略來刪掉多余的個體，保持外部檔案中個體的優越性［19］。

按照這種思路，當外部檔案中存放的非支配解超過設定值時，可以以不同個體的網格密度為評價標準對外部檔案進行處理，將網格密度大的個體從檔案中刪除，直到外部檔案中的個體數量滿足要求。

4 仿真實驗與結果分析

4.1 實驗環境與參數設置

針對本文提出的地面目標火力分配問題，設彈藥資源種類為W={w1，w2，w3，w4}，彈藥資源的取值范圍上、下區間分別為［0，0，0，0］和［100，100，50，100］，彈藥資源的成本向量為C=（20，50，30，15），hi為［0，0.3］區間內的隨機值。仿真實驗所使用的操作系統為Windows10，環境為Python3.7，PyCharm版本為2021.1.3 x64。

為了驗證AG-MOWOA求解地面目標火力分配方案的有效性，在實驗模塊分別采用NSGA-Ⅱ［20］、MOPSO［21］、NSWOA［11］以及AG-MOWOA四種算法對火力分配問題進行對比分析，關于算法相關參數設置如下。

NSGA-Ⅱ：種群大小為100，迭代次數為50，存檔規模為100，交叉概率為0.8，變異概率為0.05。

MOPSO：種群大小為100，迭代次數為50，存檔規模為100，網格劃分數為10。

NSWOA：種群大小為100，迭代次數為50，存檔規模為100。

AG-MOWOA：種群大小為100，迭代次數為50，存檔規模為100，網格劃分數為10，Logistic控制參量為4。

4.2 實驗結果分析

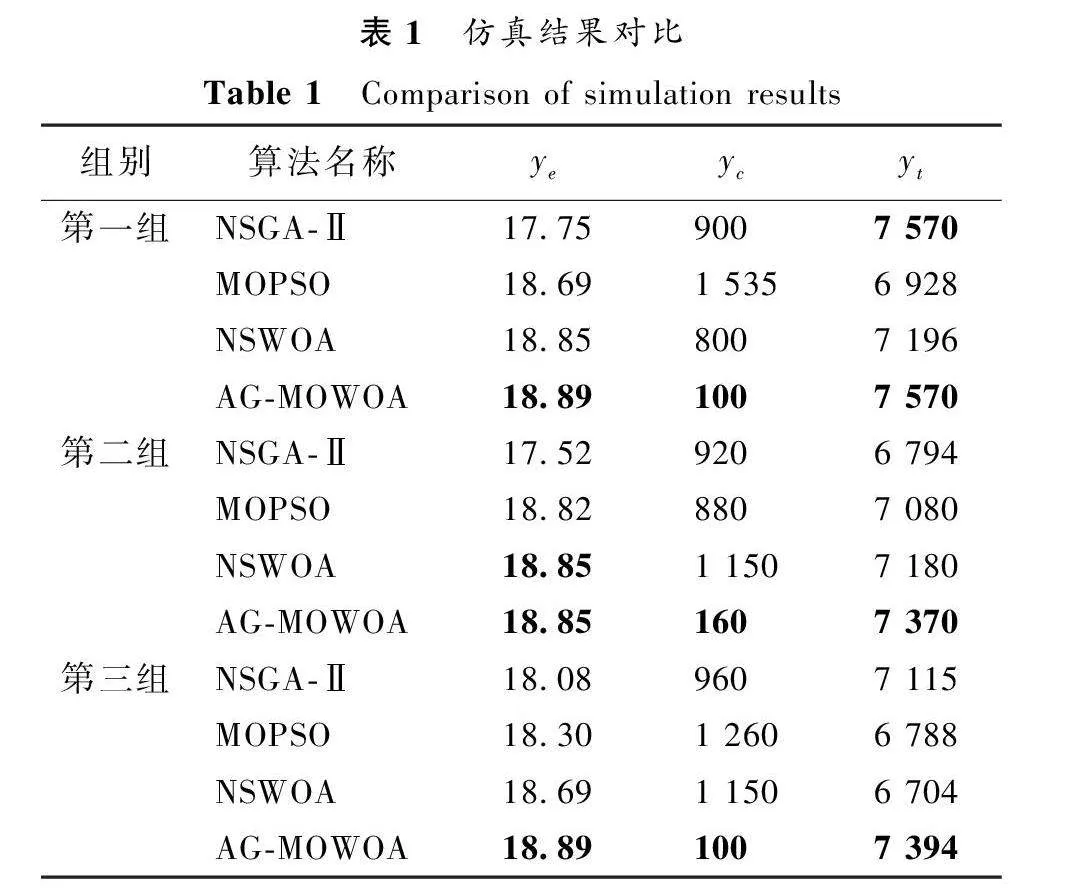
為了盡可能減少誤差，使實驗結果更加準確，這里獨立進行三組實驗，每組實驗進行10次，取這10次實驗的平均值為實驗結果，三種算法得到的最優目標函數值如表1所示。

從表1可以看出，在相同的迭代次數下，MOPSO、NSGA-Ⅱ和NSWOA得到的最優解質量不相上下，而AG-MOWOA所求得的三個最優目標函數值的質量和穩定性均優于其他三種算法，說明該算法擁有更優的全局搜索能力。

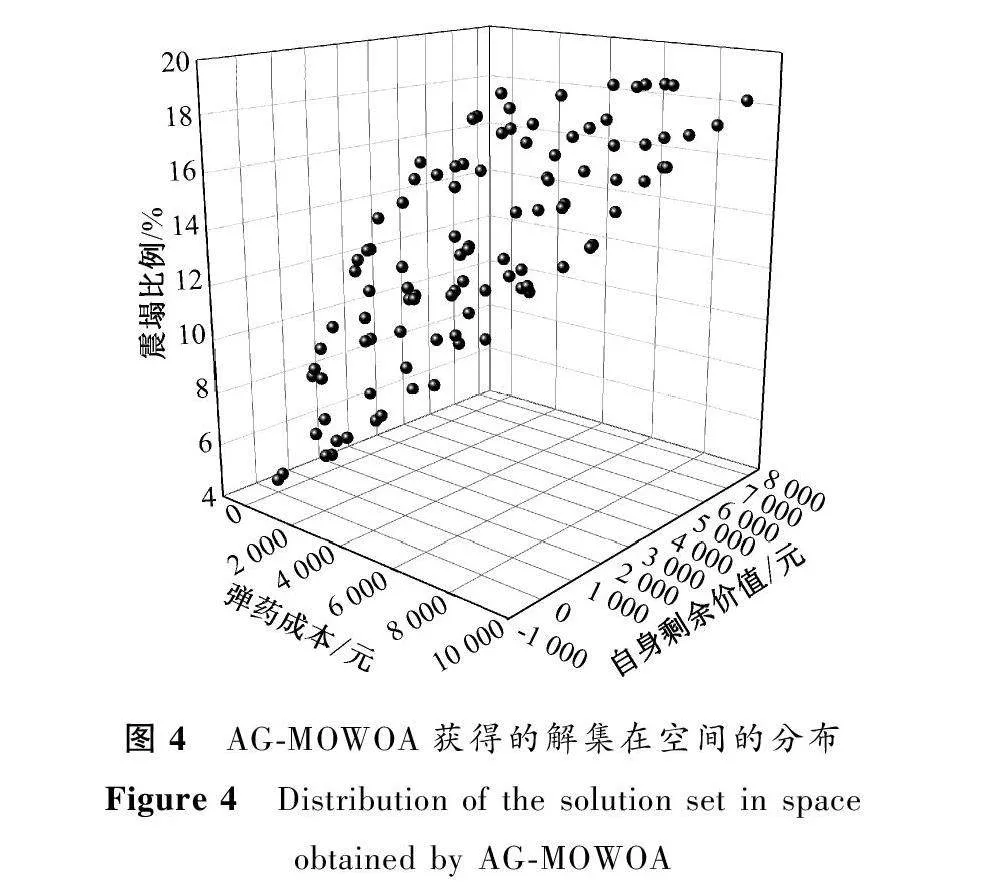
以第一組算法得到的解集分布為例，初始的解集分布如圖3所示，AG-MOWOA的分布狀況如圖4所示。從圖中可以看出，相較于初始解集， AG-MOWOA的分布更加集中，但是仍無法準確判斷是否收斂。因此，需要用更加科學的方法來對比這四種算法的效果。

4.3 算法性能分析

為了測試各算法求解火力分配問題的性能，這里用三個指標對求得的解集進行評估，其中真實Pareto前沿取在范圍區間內均勻分布的500條真實數據。

1） 反轉世代距離（IGD）

反轉世代距離計算的是每個參考點到最近解的歐氏距離［22］，如式（16）所示，可以用來評估算法的收斂性與多樣性，IGD的值越小，算法的綜合性能就越好，

IGD（P，P*）=∑x∈P*miny∈Pdis（x，y）P*，（16）

其中：P為算法求得的Pareto前沿解集；P*為真實Pareto前沿上均勻的參考點；P*為參考點的數量；dis（x，y）為點x與點y之間的歐氏距離。

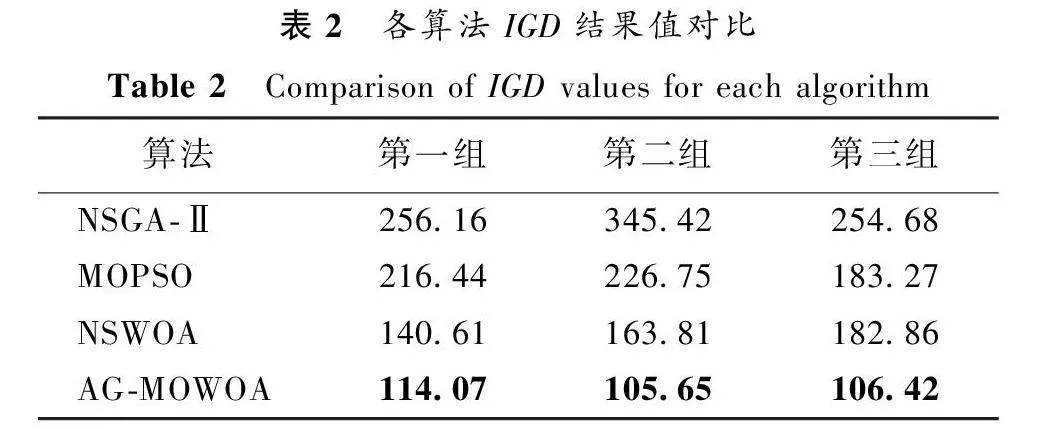
通過計算得到的最小歐氏距離分布如圖5所示，IGD值大小如表2所示。

從圖5中可以看出AG-MOWOA求得的解集距離參考Pareto前沿的距離分布更加均勻，結合表2可以看出AG-MOWOA求得的IGD值更小，表明該算法獲得的解集更加均勻，并且在收斂性和多樣性上都占明顯優勢。

2） C-metric解集覆蓋率

解集覆蓋率可以表示不同算法得到解集之間的互相支配關系，如式（17）所示，分子為滿足存在解集A中的點支配解集B中的任意條件的點的個數，分母為解集B中解的個數，如果解集覆蓋率C（A，B）大于C（B，A），則說明解集A的個體更接近真實Pareto前沿。

C（A，B）={x∈By∈A：yx}B，（17）

其中：A和B表示需要比較的兩個解集；yx表示y支配x；·表示滿足括號內條件的個數。

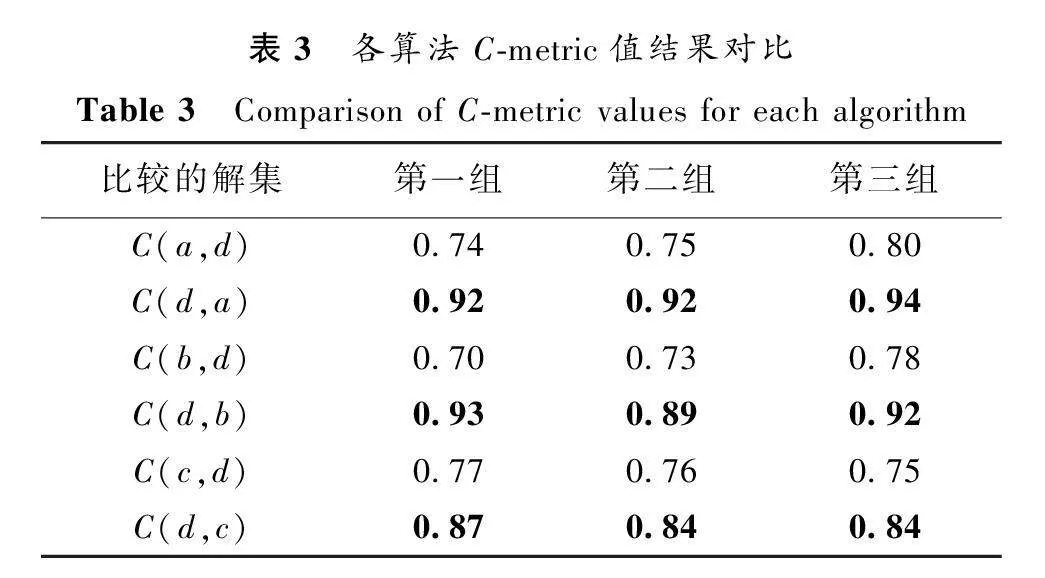
記NSGA-Ⅱ為算法a，MOPSO為算法b，NSWOA為算法c，AG-MOWOA為算法d，計算三組實驗得到的各算法解集覆蓋率如表3所示。

從表3中可以看到，在三組實驗中AG-MOWOA的解集覆蓋率遠大于其他三種算法，表明該算法求得的解集相較于其他三種算法質量更高，更接近真實Pareto前沿。

3） 算法消耗時間

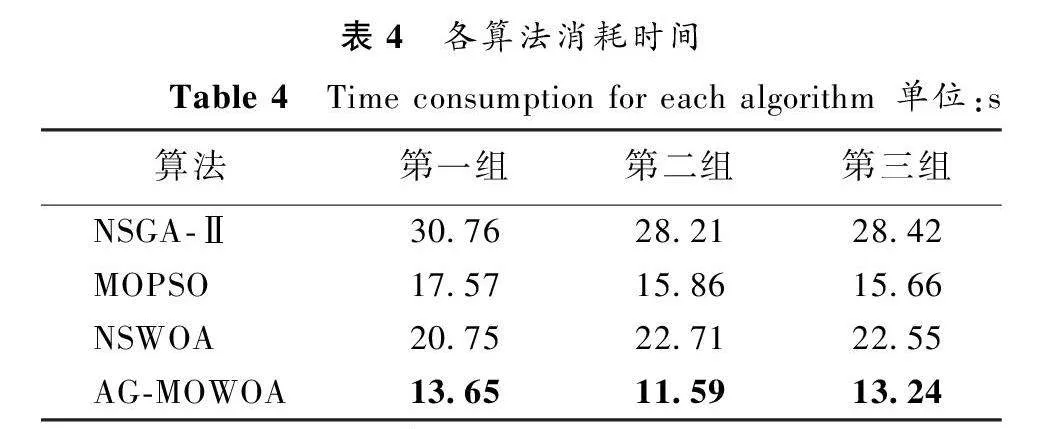
每組10次實驗的平均算法消耗時間統計得到的數據如表4所示。從表4中可以看出AG-MOWOA在消耗時間上也遠遠小于其他三種算法。

通過以上評估，可以看出本文提出的AG-MOWOA在收斂性、多樣性、均勻性、消耗時間上較其他算法均有提升，可以有效解決本文提出的火力分配問題。

5 結語

本文針對火力分配問題構建了以震塌比例、彈藥成本和自身剩余價值為目標函數的火力分配模型，并提出了一種自適應網格多目標鯨魚優化算法，該方法采用混沌映射初始化種群，使初始種群在可行解空間內分布更加均勻，利用自適應網格劃分法為個體編號，不但可以挑選出最優個體，還能減少算法計算量，最后引入Pareto存檔進化策略有效增加了種群的多樣性。仿真實驗結果表明，本文提出的算法在收斂性、多樣性、運行速度等多方面性能較其他算法都有提升。針對多于三個目標函數的火力分配問題的求解是本文所提算法今后需要改進的方向。

參考文獻：

［1］ 劉志超， 石章松， 姜濤， 等. 基于最小資源損耗的火力分配研究［J］. 火力與指揮控制， 2018， 43（6）： 167-170.

LIU Z C， SHI Z S， JIANG T， et al. Research on method of weapon-target assignment based on the minimal resource loss［J］. Fire control & command control， 2018， 43（6）：167-170.

［2］ 于博文， 呂明. 基于改進NSGA-III算法的動態武器協同火力分配方法［J］. 火力與指揮控制， 2021， 46（8）：71-77， 82.

YU B W， LYU M. Method for dynamic weapon coordinative firepower distribution based on improved NSGA-Ⅲ algorithm［J］. Fire control & command control， 2021， 46（8）：71-77， 82.

［3］ 張明雙， 徐克虎. 基于最小火力浪費的火力優化分配［J］. 電光與控制， 2020， 27（9）： 55-59.

ZHANG M S， XU K H. Optimal firepower distribution based on minimum firepower waste［J］. Electronics optics & control， 2020， 27（9）： 55-59.

［4］ KONG L R， WANG J Z， ZHAO P. Solving the dynamic weapon target assignment problem by an improved multiobjective particle swarm optimization algorithm［J］. Applied sciences， 2021， 11（19）： 9254.

［5］ 王峰， 張衡， 韓孟臣， 等. 基于協同進化的混合變量多目標粒子群優化算法求解無人機協同多任務分配問題［J］. 計算機學報， 2021， 44（10）： 1967-1983.

WANG F， ZHANG H， HAN M C， et al. Co-evolution based mixed-variable multi-objective particle swarm optimization for UAV cooperative multi-task allocation problem［J］. Chinese journal of computers， 2021， 44（10）： 1967-1983.

［6］ 聶俊峰， 陳行軍， 蘇琦. 基于NSGA-Ⅲ算法的集群目標來襲火力分配建模與優化［J］. 兵工學報， 2021， 42（8）：1771-1779.

NIE J F， CHEN X J， SU Q. Modeling and optimization of weapon-target assignment for group targets defense based on NSGA-Ⅲ algorithm［J］. Acta armamentarii， 2021， 42（8）：1771-1779.

［7］ MIRJALILI S， LEWIS A. The whale optimization algorithm［J］. Advances in engineering software， 2016， 95： 51-67.

［8］ SUN Y J， CHEN Y. Multi-population improved whale optimization algorithm for high dimensional optimization［J］. Applied soft computing， 2021， 112： 107854.

［9］ 郭振洲， 王平， 馬云峰， 等. 基于自適應權重和柯西變異的鯨魚優化算法［J］. 微電子學與計算機， 2017， 34（9）： 20-25.

GUO Z Z， WANG P， MA Y F， et al. Whale optimization algorithm based on adaptive weight and cauchy mutation［J］. Microelectronics & computer， 2017， 34（9）： 20-25.

［10］REN G， YANG R H， YANG R Y， et al. A parameter estimation method for fractional-order nonlinear systems based on improved whale optimization algorithm［J］. Modern physics letters B， 2019， 33（7）： 1950075.

［11］JANGIR P， JANGIR N. Non-dominated sorting whale optimization algorithm （NSWOA）： a multi-objective optimization algorithm for solving engineering design problems［J］. Global journals of research in engineering，2017： 17： 15-42.

［12］梁倩. 基于反向精英保留和Levy變異的多目標鯨魚優化算法［J］. 現代計算機， 2021（18）： 25-31.

LIANG Q. Multi-objective whale optimization algorithm based on reverse elite retention and Levy mutation［J］. Modern computer， 2021（18）： 25-31.

［13］SUN H， CAO A R， HU Z Y， et al. A novel quantile-guided dual prediction strategies for dynamic multi-objective optimization［J］. Information sciences， 2021， 579： 751-775.

［14］SONG Z H， LIU T， LIN Q Z. Multi-objective optimization of a solar hybrid CCHP system based on different operation modes［J］. Energy， 2020， 206： 118125.

［15］WANG Y K， WANG S L， LI D， et al. An improved multi-objective whale optimization algorithm for the hybrid flow shop scheduling problem considering device dynamic reconfiguration processes［J］. Expert systems with applications， 2021， 174： 114793.

［16］孫海文， 謝曉方， 孫濤， 等. 改進型布谷鳥搜索算法的防空火力優化分配模型求解［J］. 兵工學報， 2019， 40（1）： 189-197.

SUN H W， XIE X F， SUN T， et al. Improved cuckoo search algorithm for solving antiaircraft weapon-target optimal assignment model［J］. Acta armamentarii， 2019， 40（1）： 189-197.

［17］WANG L， LIU X Y， SUN M H， et al. A new chaotic starling particle swarm optimization algorithm for clustering problems［J］. Mathematical problems in engineering， 2018， 2018： 1-14.

［18］方冰， 李太勇， 吳江. 一種基于網格劃分的自適應粒子群優化算法［J］. 計算機應用研究， 2010， 27（11）：4136-4139.

FANG B， LI T Y， WU J. Grid-based adaptive particle swarm optimization［J］. Application research of computers， 2010， 27（11）：4136-4139.

［19］KNOWLES J D， CORNE D W. Approximating the nondominated front using the Pareto archived evolution strategy［J］. Evolutionary computation， 2000， 8（2）： 149-172.

［20］DEB K， PRATAP A， AGARWAL S， et al. A fast and elitist multiobjective genetic algorithm： NSGA-II［J］. IEEE transactions on evolutionary computation， 2002， 6（2）： 182-197.

［21］COELLO C A， LECHUGA M S. MOPSO： a proposal for multiple objective particle swarm optimization［C］∥Proceedings of the 2002 Congress on Evolutionary Computation. Piscataway： IEEE Press， 2002： 1051-1056.

［22］ISHIBUCHI H， MASUDA H， TANIGAKI Y， et al. Difficulties in specifying reference points to calculate the inverted generational distance for many-objective optimization problems［C］∥IEEE Symposium on Computational Intelligence in Multi-criteria Decision-making. Piscataway： IEEE Press， 2015： 170-177.