融合內容與嵌入強化拓撲的半監督社團檢測

摘要： 挖掘網絡中的社團結構是復雜網絡分析的關鍵任務，但在現實應用中如何進一步提高社團檢測性能仍極具挑戰性。鑒于屬性網絡中的節點內容和網絡嵌入均蘊含有社團結構信息，提出一種基于非負矩陣分解融合節點內容和嵌入強化拓撲的半監督方法。首先，基于生成框架重構拓撲和內容，以構建融合拓撲和內容的基本模型；然后，利用拓撲相似性構造must-link先驗信息，同時由Node2Vec計算網絡嵌入；最后，使用矩陣補全技術將先驗信息和網絡嵌入引入模型，形成融合內容、網絡嵌入的半監督社團檢測模型。在合成和真實網絡上的實驗結果充分驗證了新模型的良好競爭力。

關鍵詞： 社團檢測； 屬性網絡； 半監督； 節點內容； 嵌入強化

中圖分類號： TP391

文獻標志碼： A

文章編號： 1671-6841（2024）06-0046-08

DOI： 10.13705/j.issn.1671-6841.2023143

Combination of the Content and Embedding-enhanced Topology for Semi-supervised Community Detection

XU Weizhong1， LU Yang1， CAO Jinxin1， JU Hengrong1， DING Weiping1， JIN Di2

（1.School of Information Science and Technology， Nantong University， Nantong 226019， China；

2.College of Intelligence and Computing， Tianjin University， Tianjin 300350， China）

Abstract： Mining the community structure in a network was a key task in complex network analysis， but how to further improve the performance of community detection in practical applications was still highly challenging. Considering that both node content and network embedding in attribute networks contain the information of community structure， a semi-supervised method based on non-negative matrix factorization that integrates node content and embed reinforcement topology was proposed. Firstly， based on the generated framework， a basic model that could integrate topology and content was reconstructed. Then， by utilizing the topological similarity between nodes， a must-link prior was constructed， and at the same time， the network embedding was conducted by Node2Vec. Finally， the inductive matrix completion technique was used to introduce prior information and network embedding， forming a semi-supervised community detection model that could integrate content and network embedding. The strong competitiveness of the new model was fully verified through experiments on synthetic and real networks.

Key words： community detection; attributed network; semi-supervised; node content; embedding reinforcement

0 引言

社交網絡化的數據存在于現實生活中的方方面面，比如，客戶關系網絡、在線產品評論網絡等。這些帶有節點內容的屬性網絡可建模為復雜網絡。挖掘屬性網絡中的社團結構可揭示所蘊含的結構和主要功能，具有十分重要的現實意義。社團結構檢測有廣泛的應用，如社交網絡的用戶行為和需求檢測、基因功能檢測、復雜系統特性分析、推薦系統等。

社團一般定義為同一社團的節點間鏈接稠密，而不同社團的節點間鏈接稀疏。近十幾年來，已有不同類型的社團發現方法提出［1-4］，并取得了不錯的成績。傳統方法將具有相似鏈接模式的節點集識別為社團，當面對異配、分層等復雜結構的網絡時，其性能將受到影響。一些研究人員提出了半監督社團檢測方法［5-6］，引入有限的先驗信息便可明顯提升社團檢測精度。網絡中也會存在鏈接缺失或噪聲，網絡蘊含的內容信息在社團檢測任務中可補充網絡的拓撲。Newman等［7］發現，結合內容可識別的社團結構更為準確。近幾年，網絡嵌入（network embedding）已被廣泛應用于社團檢測領域［1］。網絡嵌入運用稠密的表征向量刻畫社團結構，Jin等［2］研究發現融合網絡嵌入能夠對結構復雜的網絡進行高效挖掘。

同時融合網絡拓撲、內容信息和網絡嵌入的半監督社團檢測方法挖掘網絡中社團結構的執行力將會得到進一步提升。因為網絡中鄰居重合度高的節點往往具有相似的內容信息，它們的網絡嵌入也會很相近，被劃分到同一社團的可能性也高。本文提出了一種融合節點內容和嵌入強化鏈接的半監督社團檢測模型（embedding-enhanced link based semi-supervised community detection with node content，ELSNC）。結合生成框架和歸納矩陣補全技術構建新模型，將鄰接矩陣、節點內容特征矩陣、拓撲相似度矩陣、網絡嵌入矩陣作為模型的四個輸入源。首先，基于非負矩陣分解（non-negative matrix factorization，NMF）生成框架構建網絡拓撲子模型，設計節點-社團隸屬度矩陣以重構鄰接矩陣。接著，基于NMF與主題模型pLSA［8］理論等價性原理構建節點內容子模型，設計節點內容-主題隸屬度矩陣以重構節點內容。文檔主題即對應網絡社團。然后，運用“如果兩個節點存在鏈接且具有高度相似的拓撲結構，它們將被劃分到同一社團”的想法構造社團指示矩陣以實現先驗信息（半監督信息）的構建。再次，將網絡嵌入和先驗信息使用歸納矩陣補全技術引入拓撲子模型中。最終，使用一個平衡因子結合網絡拓撲和節點內容，使用一個鄰域超參刻畫先驗信息，以實現融合網絡拓撲、節點內容和網絡嵌入的半監督社團檢測統一模型的構建。

1 相關工作

鑒于新模型融合的信息來自不同類型，本文梳理了基于網絡拓撲社團檢測、基于內容信息社團檢測、融合網絡拓撲與節點內容社團檢測以及半監督社團檢測等相關研究工作。

在傳統模型中，基于經典的模塊度Q，Blondel等［9］提出Louvain算法，運用分層聚類實現社團發現。Yang等［10］運用NMF構建隨機塊模型，經推導獲得非負社團隸屬度以挖掘網絡中的社團。Grover等［11］設計的經典網絡嵌入模型Node2Vec是基于Deepwalk模型進行的擴展，獲取節點表征后進行聚類以挖掘社團結構。Wang等［12］使用自動編碼器優化一階和二階相似度圖的圖嵌入模型SDNE，實現了網絡嵌入社團檢測精度的提升。基于內容信息的模型MAC［13］是運用NMF和生成模型思想，實現了布爾型數據的重疊類別聚類，這表明了節點內容也具有社團結構。

關于融合拓撲與內容的模型，Yang等［14］基于生成框架，相互獨立地建模拓撲和內容信息，引入一個平衡因子構建融合二元信息的聯合模型CESNA。Wang等［15］認為節點內容能給出社團的描述，設計了基于NMF融合拓撲和內容的SCI模型，實現了對語義社團的挖掘。Yang等［16］提出的TADW模型屬于融合拓撲和內容的網絡嵌入模型，其運用矩陣分解和歸納矩陣補全技術實現二元信息的融合，獲得的網絡表征可用于社團檢測。

半監督社團檢測兼顧了網絡的異配、分層等復雜結構，通過引入網絡結構的先驗信息，實現社團結構檢測性能的提升。Yang等［17］基于子空間聚類思想，以圖正則的形式引入先驗信息，提出了NMF_LSE、NMF_SYM模型。He等［18］運用修正、懲罰兩種策略引入硬、軟約束形式的先驗信息，提出了ECD模型實現半監督社團檢測。

上述模型中，融合內容信息、引入先驗信息均可實現社團檢測性能的提升。鑒于此，若在模型中同時融合內容、網絡嵌入，并引入先驗信息，其擴展性將會得到提升，其魯棒性、社團結構檢測能力也將會進一步提升。

2 構建ELSNC模型

2.1 構建網絡拓撲子模型

用n表示網絡中的節點個數，m表示鏈接條數，l表示節點內容特征維度。一個無向、非加權的屬性網絡可以形式化為G=（V， E， F），其中：V={v1，v2，…，vn}，代表節點集；E={e1，e2，…，em}，代表邊集；F={f1，f2，…，fn}，代表節點內容特征集。基于以上信息，構建鄰接矩陣A∈Rn×n，節點內容特征矩陣為B∈Rn×l，網絡嵌入矩陣為U，社團指示矩陣為C。

鄰接矩陣A的每行表示某一節點在網絡中的鏈接狀態特征。設置一組參數xit描述節點vi隸屬于第t個社團的傾向，另一組參數wtj描述第t個社團蘊含第j個基特征的傾向。那么，xitwjt則描述社團t中節點vi和vj之間存在鏈接的數量。則包含k個社團的屬性網絡G中，vi和vj之間鏈接期望數可形式化為

a^ij=∑kt=1xitwjt， i=1，2，…，n，j=1，2，…，n，（1）

公式（1）的矩陣化形式為A^=XWT，擬合鄰接矩陣A。拓撲子模型的目標函數為

lossto（X，W）=‖A-A^‖2F=‖A-XWT‖2F。（2）

2.2 構建內容拓撲子模型及基本模型

鑒于pLSA主題模型［8］與NMF模型的理論相似性，可將每個節點所包含的內容對應于一篇文檔，屬性對應文檔中單詞。參數xit刻畫節點內容-主題隸屬度，設置hjt描述文章第t個主題包含第j個單詞的傾向，xithjt指示節點vi隸屬于第t個社團，且蘊含第j個屬性的可能性。則節點vi與第j個屬性之間的關聯可表示為

bij=∑kt=1xithjt， i=1，2，…，n，j=1，2，…，l，（3）

公式（3）的矩陣化形式為B^=XHT，擬合觀測節點內容特征矩陣B。內容子模型的目標函數可形式化為

lossco（X，H）=‖B-B^‖2F=‖B-XHT‖2F。（4）

公式（4）中，文檔集的主題對應于網絡的社團，則節點內容-主題隸屬度即為節點-社團隸屬度。這樣便可對公式（2）和（4）所表示的子模型進行融合，并使用超參α控制內容子模型的貢獻。至此融合了拓撲和內容并構建基本模型，其目標函數可形式化為

Oto+co（X，W，H）=

argX，W，H≥0min‖A-XWT‖2F+α·‖B-XHT‖2F。（5）

2.3 引入先驗信息

本文基于網絡中節點的拓撲結構設置半監督信息，即must-link先驗信息。對于某一節點vi，其網絡拓撲結構可以由它的鄰居節點來描述，即D（i）={vj∈V（vi，vj）∈E}∪{vi}。那么，網絡中節點的拓撲相似度矩陣S={sij}∈Rn×n可計算為

sij=D（i）∩D（j）D（i）×D（j）。（6）

基于想法“如果兩個節點存在鏈接且拓撲結構相似度高，那么，它們之間存在must-link約束，將被分配到同一個社團”，使用以下方式對約束矩陣Ω={ωij}∈Rn×n進行構造

ωij=1，aij=1，sij>ε，

0，aij=0，（7）

其中超參ε控制must-link生成的數量。很明顯，在Ω對應無向圖中任一連通分量下所包含的節點間均具有must-link約束。進一步，設置指示矩陣C∈Rn×p表示頂點-連通分量隸屬分布，用以刻畫先驗信息。此處C可視為節點的額外特征。基于歸納矩陣補全思想，通過引入一個非負的輔助矩陣Y∈Rp×k，則節點-社團隸屬度X可表示為

X=CY，（8）

運用公式（8）引入先驗信息到基本模型（5），目標函數為

Osemi+to+co（Y，W，H）=

argY，W，H≥0min‖A-CYWT‖2F+α·‖B-CYHT‖2F。（9）

2.4 引入網絡嵌入信息

Node2Vec算法［10］將鄰接矩陣轉化為網絡嵌入矩陣U∈Rn×p。本文將鄰接矩陣A視為特征矩陣，對于鄰接矩陣的特征化描述可運用奇異值分解等形式。這里同樣借鑒矩陣補全的思想將已獲取的網絡嵌入U引入拓撲子模型中［15］。特征矩陣W可由網絡嵌入U作為其額外特征進行表示，可形式化為

W→UW，（10）

用公式（10）將網絡嵌入引入帶有先驗信息的基本模型（9）中。統一融合模型的目標函數為

Lfinal（Y，W，H）=Osemi+to+emb+co（Y，W，H）=

argY，W，H≥0min‖A-CYWTUT‖2F+

α·‖B-CYHT‖2F+β·‖W‖2F，（11）

其中，最后一項為正則項，防止模型過擬合。至此，完成了對ELSNC模型的構建。該模型統一化融合網絡拓撲、節點內容、網絡嵌入和先驗信息。通過模型優化學習參數矩陣Y后，再結合指示矩陣C可計算節點-社團隸屬度。基于節點-社團隸屬度矩陣進行聚類，實現社團檢測。

2.5 ELSNC模型的算法偽代碼

模型ELSNC的具體實現過程可由如下偽代碼呈現。

算法1 ELSNC的算法

輸入： 鄰接矩陣A，節點內容特征矩陣B，社團個數k，平衡因子α、β，領域超參ε，閾值ξ，最大迭代次數τmax。

輸出： 社團隸屬度矩陣X。

①運用公式（6）計算A的拓撲相似度矩陣S，再使用公式（7）設計先驗信息的指示矩陣C；

②基于A用Node2Vec算法計算網絡嵌入U；

③隨機初始化Ynew、Wnew和Hnew；

④while （Lfinal （Y，W，H）（τ）-Lfinal（Y，W，H）（τ-1）<ξ or τ>τmax）

⑤令Yold=Ynew，Wold=Wnew，Hold=Hnew，運用公式（13）、（14）和（15）更新Ynew、Wnew和Hnew；

⑥運用公式（11）計算Lfinal（Y，W，H）；

⑦τ=τ+1；

⑧end while

⑨獲得最優Y，基于公式（8）計算X；

⑩返回X。

3 ELSNC模型優化

模型ELSNC包含了三個參數矩陣Y、W和H。秩形式中，y=f（x），則trace［y］=tr［f（x）］。為了進行模型推導，現將新模型的目標函數（11）轉為秩的形式L（Y，W，H），然后，運用卡羅需-庫思-塔克（Karush-Kuhn-Tucker，KKT）條件［19］的梯度下降法進行模型參數更新規則求解。目標函數（11）的秩形式L（Y，W，H）為

L（Y，W，H）=trace［Lfinal（Y，W，H）］=

tr［（A-CYWTUT）（A-CYWTUT）T］+

α·tr［（B-CYHT）（B-CYHT）T］+β·tr（WWT）=

tr［（A-CYWTUT）（AT-UWYTCT）］+

α·tr［（B-CYHT）（BT-HYTCT）］+

β·tr（WWT）=tr（AAT）-2·tr（AUWYTCT）+

tr（CYWTUTUWYTCT）+

α·tr（BBT）-2α·tr（BHYTCT）+

α·tr（CYHTHYTCT）+β·tr（WWT）。（12）

式（12）關于參數矩陣Y的偏導為

YL（Y，W，H）=

-2·Ytr（AUWYTCT）+Ytr（CYWTUTUWYTCT）-

2α·Ytr（BHYTCT）+α·Ytr（CYHTHYTCT）=

-2CTAUW+2CTCYWTUTUW+

2α·CTBH+2α·CTCYHTH。

根據KKT條件［19］，參數矩陣Y的更新規則為

ynewij=yoldij·｛-Y｝ij｛+Y｝ij=

yoldij·（CTAUW+α·CTBH）ij（CTCYWTUTUW+α·CTCYHTH）ij。（13）

同樣，式（12）關于參數矩陣W的偏導為

WL（Y，W，H）=-2·Wtr（AUWYTCT）+

Wtr（CYWTUTUWYTCT）+β·tr（WWT）=

-2·UTACY+2·UTUWYTCTCY+2β·W。

而W的更新規則為

wnewij=woldij·｛-W｝ij｛+W｝ij=

woldij·（UTACY）ij（UTUWYTCTCY+β·W）ij。（14）

式（12）關于參數矩陣H的偏導為

HL（Y，W，H）=-2α·Htr（BHYTCT）+

α·Htr（CYHTHYTCT）=

-2α·BCY+2α·HYTCTCY。

同理可求參數矩陣H的更新規則為

hnewij=holdij·｛-H｝ij｛+H｝ij=holdij·（BCY）ij（HYTCTCY）ij。（15）

新模型更新過程為：首先，隨機初始化非負矩陣Y、W和H；然后，分別基于更新規則（14）、（16）和（18）對Y、W和H進行迭代更新，直至損失函數（11）收斂。最后，運用公式（8）計算出節點社團隸屬度，并檢測社團。

4 分析實驗

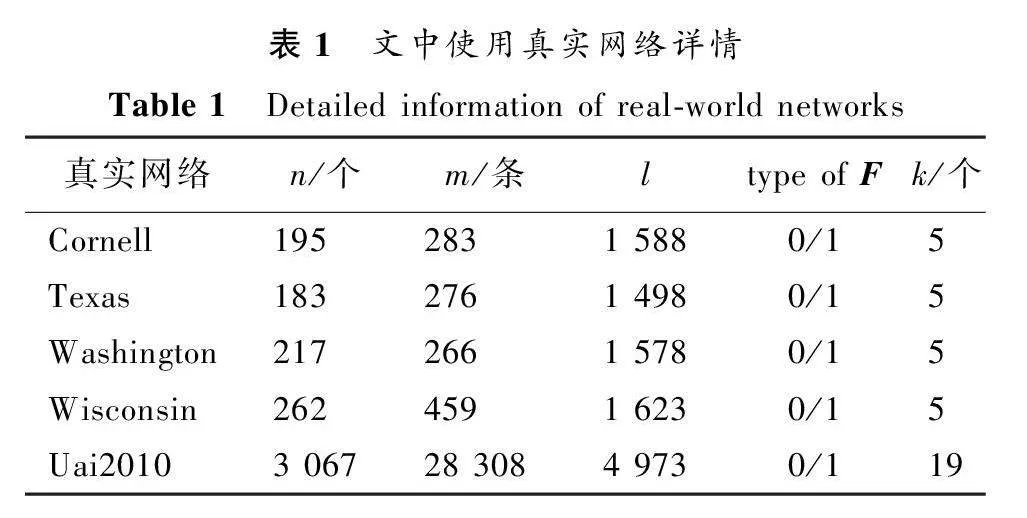
實驗使用的數據有帶有內容的GN、LFR人工網絡［22］，五個真實網絡［23］（詳細信息如表1所示，網絡中節點內容的類型用type of F表示）。對比模型包含：基于拓撲的模型有Louvain［9］、NMF［10］、Node2Vec［11］和SDNE［12］；基于內容的模型有MAC［13］；融合拓撲和內容的模型有CESNA［14］、SCI［15］、TADW［16］；半監督社團檢測模型有NMF_LSE［17］、NMF_SYM［17］、ECD［18］。

在對ELSNC性能分析前，先在帶有內容的GN網絡中對超參α、β和ε進行調節。后在帶有內容的LFR人工網絡和真實網絡上對比ELSNC模型與當前流行的社團檢測模型識別社團的能力。實驗中，使用了社團檢測領域常用的評價方法標準互信息熵（normalized mutual information，NMI）［20］和調整蘭德系數（adjusted rand index，ARI）［21］。

4.1 超參數α、β和ε的調節

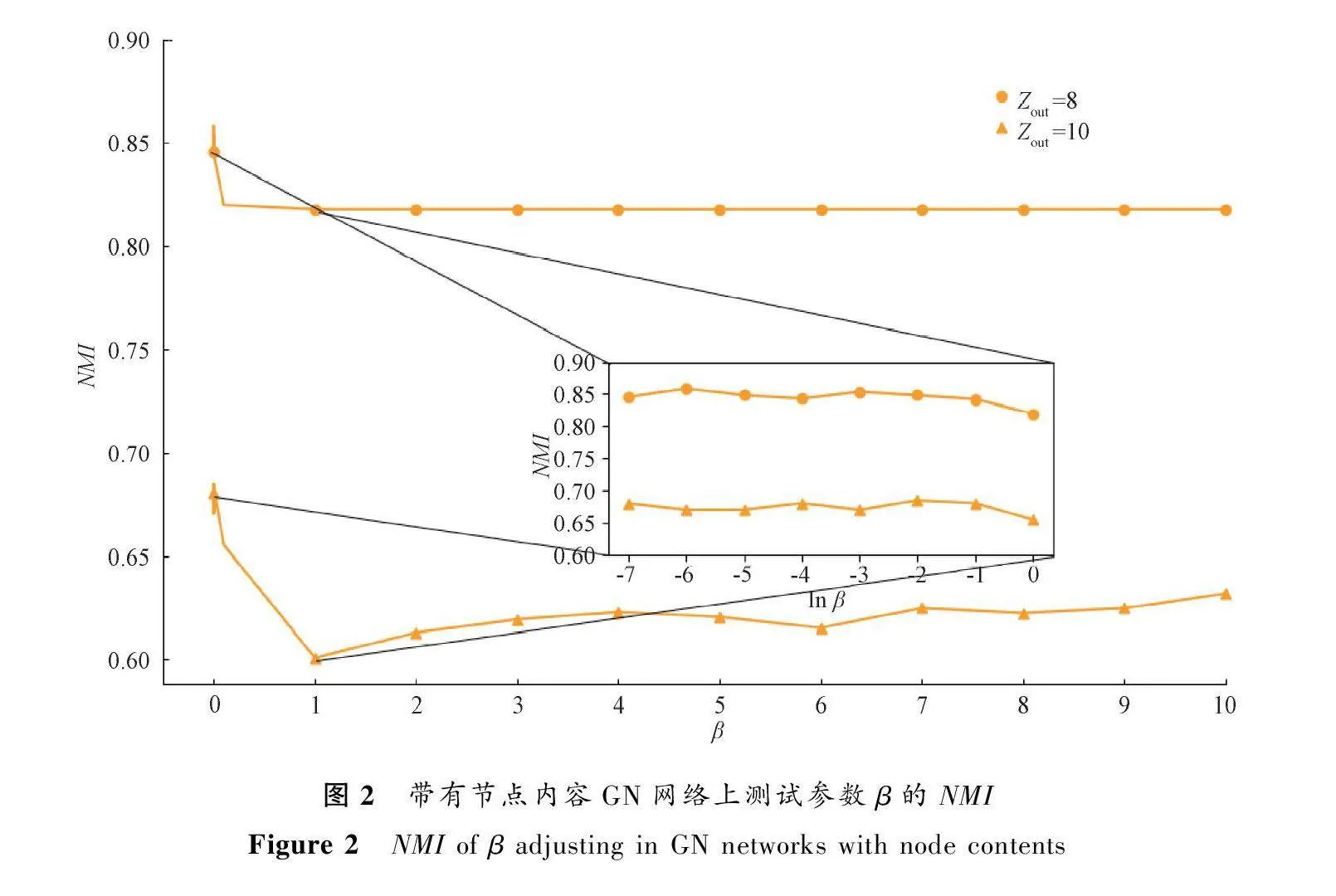
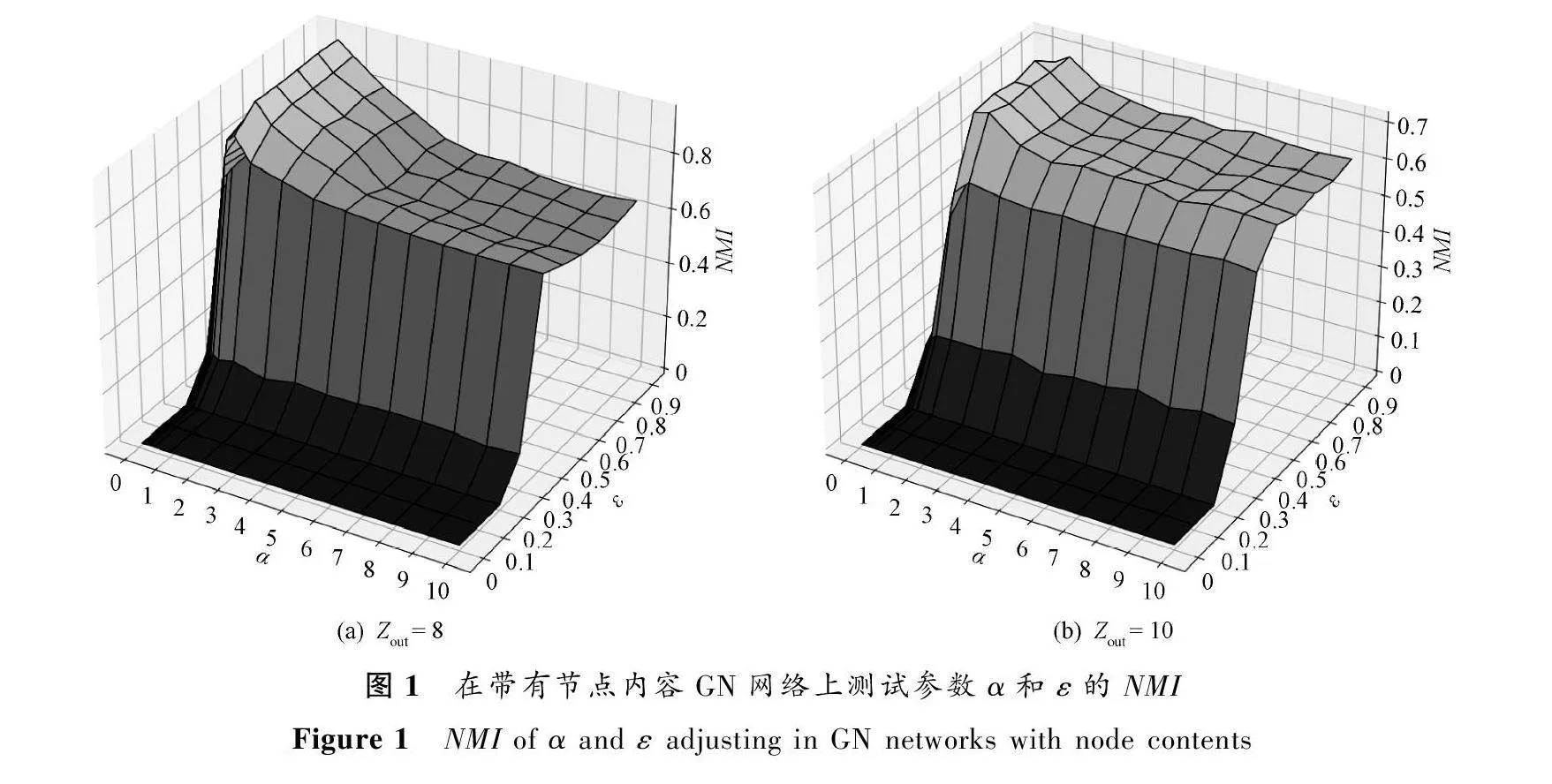
在帶有內容的人工GN網絡上對模型超參數進行測試，設定網絡生成參數Zout為8和10，社團結構相對模糊，便于測試模型中超參數α、β和ε的敏感性。

首先，固定超參數β，調節超參數α和ε。設定搜索區域為0.1<α<10（0.1<α<1時，α設為1/10、

1/8、1/6、1/4、1/2）、0.1<ε<1，對α和 ε執行網格搜索以確定最佳超參數，Zout分別為8和10時，得到的NMI值變化趨勢如圖1所示。可以發現，當（α， ε）=（0.5，0.8）時，ELSNC的NMI精度在兩個帶有內容GN網絡上均取得峰值，因此我們將（0.5，0.8）作為 （α， ε）的推薦值。然后，固定（α， ε）=（0.5， 0.8），Zout分別為8和10時測試超參β，結果如圖2所示。同理，將超參數β的推薦值設為10-3。需要說明，首先，把搜索區域設置為0<β<10，我們發現峰值出現的區域為0<β<1；然后，為了提高超參數調節的分辨率，使β分別取10-1、10-2、10-3、10-4、10-5、10-6、10-7，觀察是否取得峰值精度。將上述推薦值作為后續實驗中新模型ELSNC的超參數默認設置。

4.2 在人工網絡上的對比實驗

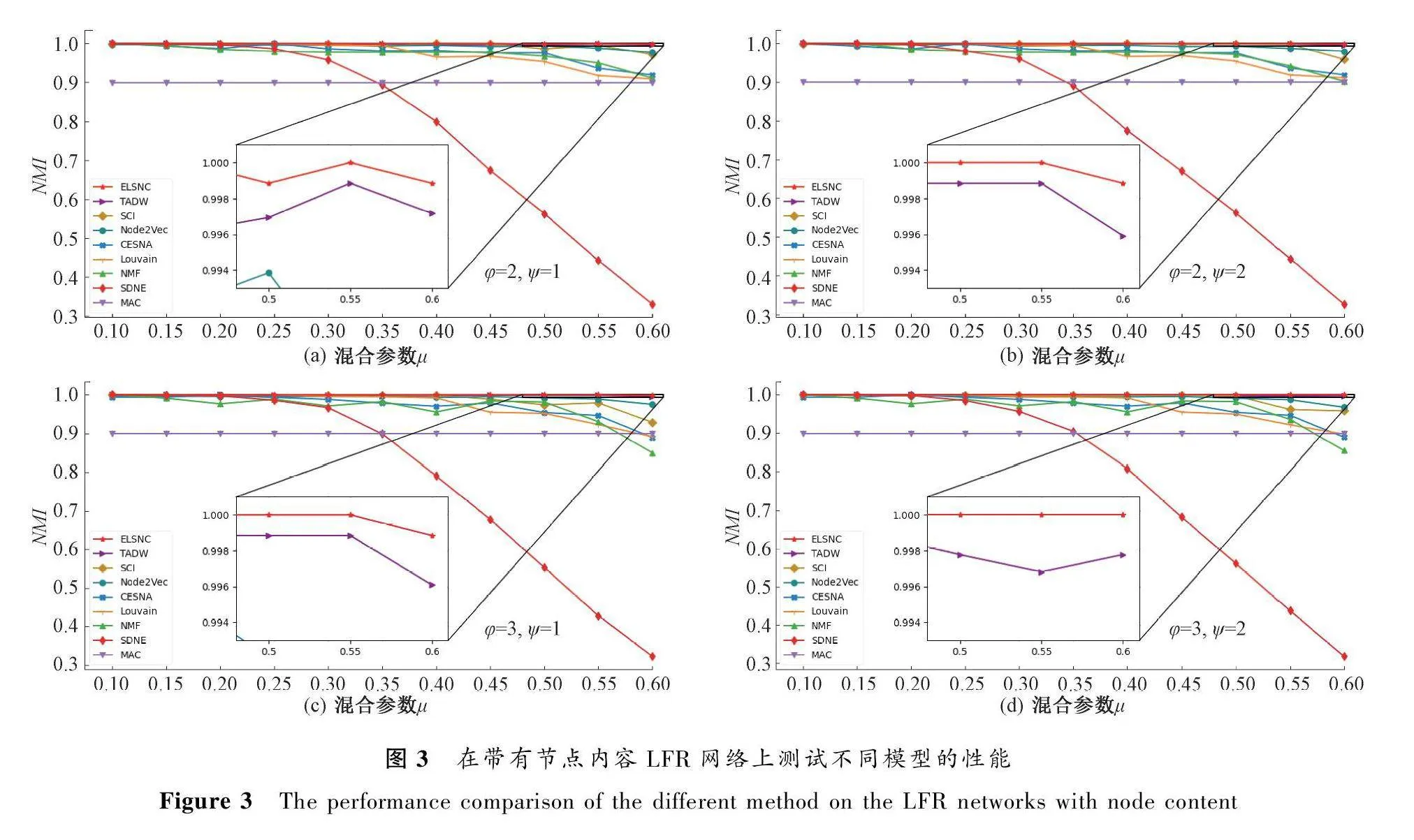
在可控的網絡中，檢驗模型ELSNC社團結構檢測的能力。對于網絡規模n=1 000，帶有內容的LFR網絡，用混合參數μ控制節點度的比值以及此節點與社團外部其他節點之間鏈接數量，μ值越大，網絡中社團結構越模糊，則模型的NMI精度曲線下降越緩慢，其魯棒性越高、執行力更強。

如圖3所示，隨著μ值增大，不同模型的NMI值均呈下降趨勢。圖3中ELSNC模型的NMI曲線下降速度均慢于其他模型，這充分表明了ELSNC在社團結構檢測的性能上具有強大競爭力。實驗中，基于內容的社團檢測模型MAC的NMI曲線顯示為一條水平線，這是由于不同模糊程度的網絡設置共享同一節點內容信息。同時，還可以發現，融合拓撲與內容的TADW、SCI和CESNA模型總體的社團結構檢測性能高于基于拓撲的NMF、Louvain模型。基于網絡嵌入的Node2Vec、SDNE模型表現不統一，但是，融合網絡嵌入和內容信息的TDAW模型的社團檢測能力總體上排名第二，說明網絡嵌入的模型對社團檢測具有良好的輔助作用。綜合分析，同時融合內容信息、網絡嵌入和先驗信息（即半監督信息）能夠進一步增強模型ELSNC社團檢測的性能。

4.3 在真實網絡上的對比實驗

在真實網絡上測試ELSNC模型與不同對比模型性能的實驗中，基準模型中的參數設置均參照原作者的默認設置。由于Yang等［17］沒有明確說明NMF_LSE、NMF_SYM模型中must-link的數量，同時考慮表1中真實網絡的期望鏈接比為m：［（n（n-1）/2）］=1.48%，因此，對于NMF_LSE、NMF_SYM模型，在實驗中引入（n（n-1）/2）×2%數量的must-link，即大于且接近m。

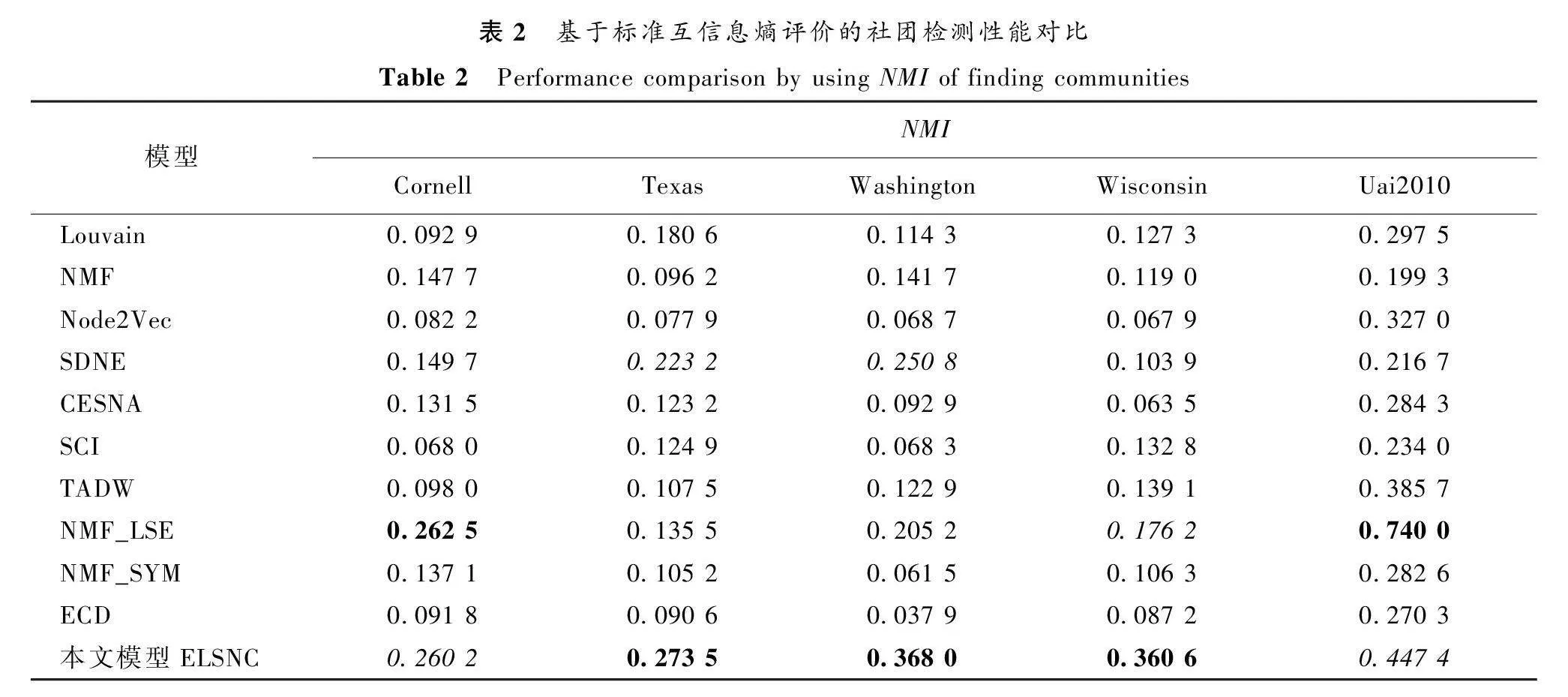
在不同真實網絡上，模型ELSNC與其他對比模型基于NMI的性能對比結果如表2所示，加粗、斜體的數值分別表示最佳、第二佳結果。可以看出，模型ELSNC在Texas、Washington和Wisconsin上取得最佳結果，在Cornell、Uai2010上取得了第二佳的結果。這表明模型ELSNC在社團檢測方面具有較強的性能。這也說明，同時融合拓撲、節點內容、網絡嵌入和先驗信息比融合拓撲與節點內容或是融合網絡嵌入與網絡拓撲能進一步識別精確的網絡社團。

關于模型NMF_SYM在Uai2010上取得較高精度，這是由于該模型中使用must-link的數量比ELSNC模型超過66倍，其獲得先驗信息描述的社團結構也更為清晰。一般地，半監督社團檢測模型結合有限的先驗信息即可實現社團檢測性能的明顯提升。但是，ELSNC模型在Uai2010上還是取得了第二佳的結果。

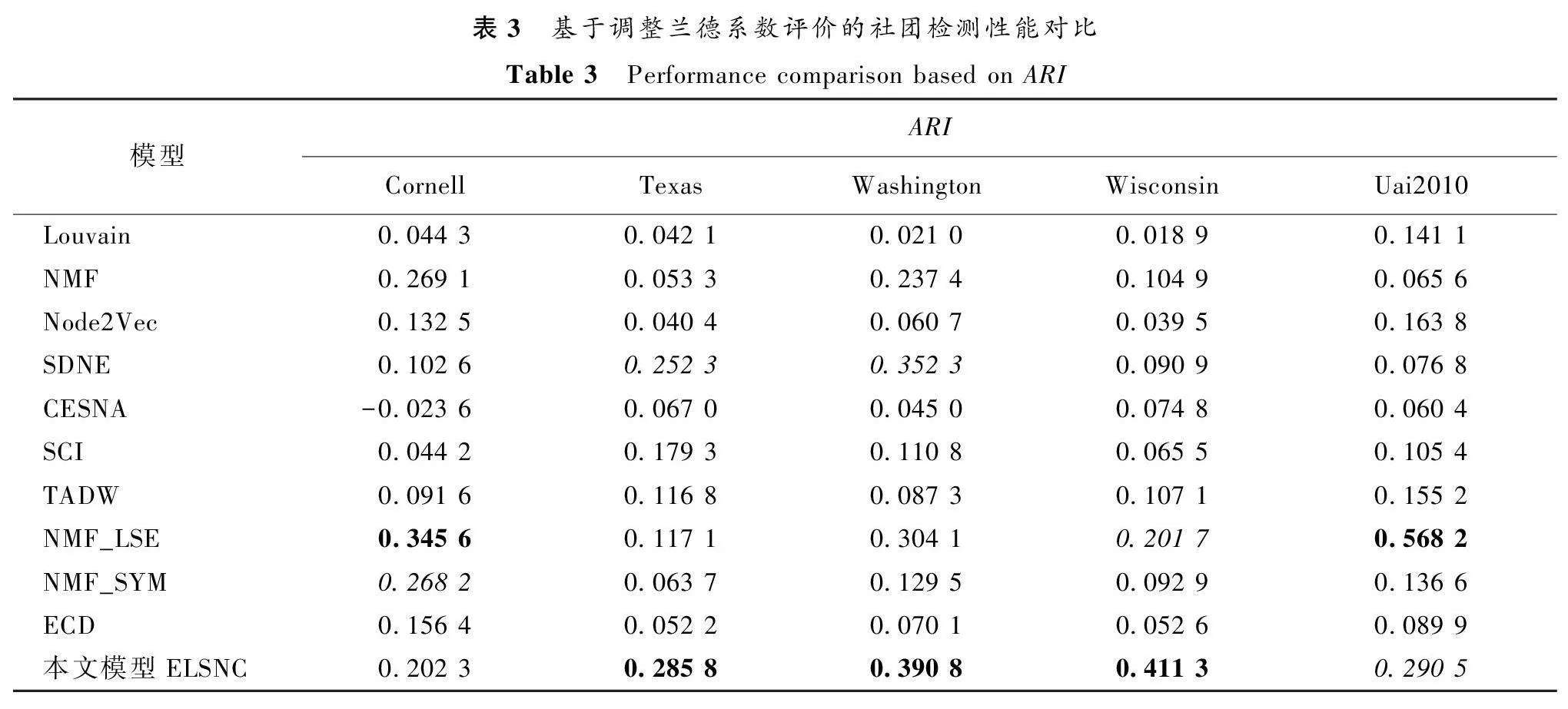
表3展示了模型ELSNC與其他社團檢測模型基于ARI性能對比結果，加粗、斜體的數值分別表示最佳、第二佳結果。ARI是聚類、社團檢測領域中常用且與模型、算法類型無關的評價方法，因此，社團檢測性能評價結果更為公平。可以看到，模型ELSNC在Texas、Washington和Wisconsin上社團結構檢測的性能獲得最佳，在Uai2010上社團檢測的性能取得第二佳，在Cornell上的結果為第三佳。綜合上述分析，對比實驗驗證了融合拓撲、內容、網絡嵌入和先驗信息可以進一步提高社團檢測模型在屬性網絡中社團結構檢測的性能以及魯棒性。

5 結論

本文提出了一種同時融合網絡拓撲、節點內容和網絡嵌入的半監督社團檢測模型ELSNC。該模型不僅能利用節點內容緩解網絡噪聲的影響，也可借助網絡嵌入刻畫社團隸屬度以減緩網絡拓撲稀疏的負面影響。還使用拓撲結構生成先驗信息來強化拓撲的社團表征能力，社團檢測能力得到進一步提升。模型的關鍵思想在于運用非負矩陣分解框架統一的融合拓撲、內容、網絡嵌入和先驗信息；基于KKT條件的梯度下降法推導新模型的參數。實驗結果驗證了ELSNC社團檢測結構的性能優越性。

本文提出的模型主要面向靜態網絡的社團檢測，還需要預先設置社團個數k。因此，未來的工作包括兩個方面：1） 設計新模型檢測動態網絡的社團結構，可以嘗試在新模型中添加正則項實現；2） 設計新模型可以進行模型選擇，即模型中預設的社團個數由k自確定，可以嘗試運用交叉驗證等方式實現模型選擇以確定k值。

參考文獻：

［1］ YU Z， FAN X H， PIETRASIK M， et al. Fragmentation coagulation based mixed membership stochastic blockmodel［J］. Proceedings of the AAAI conference on artificial intelligence， 2020， 34（4）： 6704-6711.

［2］ JIN D， ZHANG B B， SONG Y， et al. ModMRF： a modularity-based Markov random field method for community detection［J］. Neurocomputing， 2020， 405： 218-228.

［3］ HE D X， WANG Y Y， CAO J X， et al. A network embedding-enhanced Bayesian model for generalized community detection in complex networks［J］. Information sciences， 2021， 575： 306-322.

［4］ 張中軍， 于來行， 李潤川. 基于鏈路結構和轉發行為的微博社交網絡重疊社區劃分方法［J］. 鄭州大學學報（理學版）， 2021， 53（4）： 69-76.

ZHANG Z J， YU L H， LI R C. Overlapping community division method of microblog social network based on link structure and forwarding behavior［J］. Journal of Zhengzhou university （natural science edition）， 2021， 53（4）： 69-76.

［5］ LUBER M， THIELMANN A， WEISSER C， et al. Community-detection via hashtag-graphs for semi-supervised NMF topic models［EB/OL］.（2021-11-17） ［2023-03-11］. https：∥arxiv.org/abs/2111.10401.

［6］ DE SANTO A， GALLI A， MOSCATO V， et al. A deep learning approach for semi-supervised community detection in Online Social Networks［J］. Knowledge-based systems， 2021， 229： 107345.

［7］ NEWMAN M E J， CLAUSET A. Structure and inference in annotated networks［J］. Nature communications， 2016， 7： 11863.

［8］ HOFMANN T. Probabilistic latent semantic indexing［C］∥Proceedings of the 22nd Annual International ACM SIGIR Conference on Research and Development in Information Retrieval. New York： ACM Press， 1999： 50-57.

［9］ BLONDEL V D， GUILLAUME J L， LAMBIOTTE R， et al. Fast unfolding of communities in large networks［J］. Journal of statistical mechanics： theory and experiment， 2008， 2008（10）： P10008.

［10］YANG J， LESKOVEC J. Overlapping community detection at scale： a nonnegative matrix factorization approach［C］∥Proceedings of the Sixth ACM International Conference on Web Search and Data Mining. New York： ACM Press， 2013： 587-596.

［11］GROVER A， LESKOVEC J. Node2vec： scalable feature learning for networks［J］. KDD： proceedings international conference on knowledge discovery & data mining， 2016， 2016： 855-864.

［12］WANG D X， CUI P， ZHU W W. Structural deep network embedding［C］∥Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM Press， 2016： 1225-1234.

［13］STREICH A P， FRANK M， BASIN D， et al. Multi-assignment clustering for Boolean data［C］∥Proceedings of the 267+B/9ni7krdmIdJVEgfFEsFnycjT7AyGQlIsvFr4Js4=th Annual International Conference on Machine Learning. New York： ACM Press， 2009： 969-976.

［14］YANG J， MCAULEY J， LESKOVEC J. Community detection in networks with node attributes［C］∥2013 IEEE 13th International Conference on Data Mining. Piscataway： IEEE Press， 2014： 1151-1156.

［15］WANG X A， JIN D， CAO X C， et al. Semantic community identification in large attribute networks［C］∥Proceedings of the AAAI Conference on Artificial Intelligence. Palo Alto： AAAI Press， 2016： 265-271.

［16］YANG C， LIU Z Y， ZHAO D L， et al. Network representation learning with rich text information［C］∥Proceedings of the 24th International Conference on Artificial Intelligence. New York： ACM Press， 2015： 2111-2117.

［17］YANG L， CAO X C， JIN D， et al. A unified semi-supervised community detection framework using latent space graph regularization［J］. IEEE transactions on cybernetics， 2015， 45（11）： 2585-2598.

［18］HE D X， WANG H C， JIN D， et al. A model framework for the enhancement of community detection in complex networks［J］. Physica A： statistical mechanics and its applications， 2016， 461： 602-612.

［19］QI L Q， JIANG H Y. Semismooth karush-kuhn-tucker equations and convergence analysis of Newton and quasi-newton methods for solving these equations［J］. Mathematics of operations research， 1997， 22（2）： 301-325.

［20］LIU H F， WU Z H， LI X L， et al. Constrained nonnegative matrix factorization for image representation［J］. IEEE transactions on pattern analysis and machine intelligence， 2012， 34（7）： 1299-1311.

［21］YEUNG K Y， RUZZO W L. Principal component analysis for clustering gene expression data［J］. Bioinformatics， 2001， 17（9）： 763-774.

［22］CAO J X， JIN D， DANG J W. Autoencoder based community detection with adaptive integration of network topology and node contents［M］.Cham： Springer International Publishing， 2018.

［23］SEN P， NAMATA G， BILGIC M， et al. Collective classification in network data［J］. AI magazine， 2008， 29（3）： 93-106.