預測性維護任務計算卸載與資源分配聯合優化

摘要： 針對預測性維護（predictive maintenance，PdM）人工參與資源調配的問題，提出了一種基于改進人工蜂群算法（artificial bee colony，ABC）的計算卸載和資源分配方案。該方法利用遺傳算法的進化思想，改進了偵察蜂的搜尋步驟，解決了傳統人工蜂群算法容易陷入局部最優解、多樣性不足等缺點，能夠根據設備故障率生成維護成本最低的資源分配方案。仿真實驗結果表明，該算法較其他算法收斂速度更快、收斂質量更高、減少維護成本更明顯，能夠有效解決PdM場景的計算卸載和資源分配問題。

關鍵詞： 移動邊緣計算（MEC）； 預測性維護（PdM）； 任務卸載； 資源分配

中圖分類號： TP311

文獻標志碼： A

文章編號： 1671-6841（2024）06-0039-07

DOI： 10.13705/j.issn.1671-6841.2023016

Task Offloading and Resource Allocation Joint Optimization for

Predictive Maintenance

ZHANG Bo， WANG Chenghao， LI Junfeng

（School of Cyber Science and Engineering， Zhengzhou University， Zhengzhou 450002， China）

Abstract： To address the problem of manual involvement in resource allocation for predictive maintenance （PdM）， a computational offloading and resource allocation scheme based on an improved artificial bee colony（ABC） algorithm was proposed. The method utilized the evolutionary idea of genetic algorithm to improve the searching step of scout bees. The shortcomings of traditional artificial bee colony algorithms such as easy to fall into local optimal solutions and insufficient diversity were solved. The ability to generate the lowest maintenance cost resource allocation plan based on equipment failure rates.The simulation experimental results showed that the algorithm had faster convergence speed， higher convergence quality and more obvious reduction of maintenance cost than other algorithms， and could effectively solve the computational offloading and resource allocation problems of PdM scenarios.

Key words： mobile edge computing（MEC）; predictive maintenance（PdM）; task offloading; resourse allocation

0 引言

設備維護是工業生產中的一項重要組成部分，對成本和設備可靠性有重大的影響，一定程度上影響公司的競爭力。PdM的基本概念是在傳感數據的幫助下監測機器的健康狀況，以確定機器未來可能出現的退化或故障。PdM通過在必要時進行維護活動，幫助公司優化策略，而不是讓設備或組件出現故障后，或在其仍有使用壽命時進行更換。使用PdM可以減少計劃內和計劃外停機時間，降低維護成本，減少不必要的庫存和工作設備上不必要的維護活動［1］。例如，文獻［2］系統地概述了基于深度學習（deep learning，DL）的機器健康監測系統，包括四類DL架構：自動編碼器、深度信念網絡（DBN）、CNN和循環神經網絡（RNN），大部分工作針對故障識別和分類。文獻［3］提出了一個簡單的系統健康管理體系結構，并回顧了自動編碼器、CNN和RNN在系統健康管理中的應用。以上大部分PdM的研究都針對提高PdM的準確性以及完整的PdM方法，對于PdM任務的處理或分配的研究還很少。

由于PdM活動會產生大量數據，且有實時性要求，故本地計算以及卸載到云端的辦法基本無法滿足PdM的需求。移動邊緣計算（mobile edge computing，MEC）可以提供強大的通信、存儲、網絡和通信能力［4-5］。邊緣計算是指允許在網絡邊緣、云服務的下游數據和物聯網服務的上游數據上執行計算的使能技術，廣泛應用于工業物聯網、無人機和車聯網［6］。與本地計算相比，邊緣計算可以克服終端設備計算能力有限的限制。與將計算卸載到遠程云相比，邊緣計算可以避免將某些任務卸載到遠程云造成的高延遲。如文獻［7］考慮了移動設備和MEC服務器之間的帶寬限制，以及MEC服務器上的CPU資源有限的情況下，在相應的時延、頻譜資源和計算資源的約束下，提出了吞吐量最大化問題。文獻［8-9］均設置最大延遲約束，限制時間開銷都不得超過最大可容忍延遲，考慮不限制最大可容忍延遲，而是根據延遲時間構建成本函數。

本文目標是在PdM場景下，給出時間軟約束，即不具體約束延遲時間的條件下，使維護成本為第一優化目標。采用多個MEC服務器協同計算，利用邊緣計算探索高效的資源分配和任務卸載方案，最大限度使得整個PdM的成本最小。考慮任務之間分配資源的數量，給出優先級的定義，并尋找高效的任務卸載和資源分配方案。具體來說，將最終的維護成本作為最終的優化目標，據此制定了一個任務卸載和資源分配問題，并且證明其是NP-hard的。為了解決該問題，本文提出了一種低復雜度的算法，一部分是受進化策略啟發的任務卸載算法，結合了人工蜂群算法和遺傳算法。另一部分是故障優先資源分配算法，能夠在全局搜索更優的任務卸載方案，考慮任務卸載決策與計算資源分配之間的依賴性，使兩種算法之間相互作用。

1 系統模型與問題描述

1.1 邊緣計算延遲模型

本節詳細介紹卸載模型。有多個設備表示為N={N1，N2，…，Ni，…，Nn}，設備在運行過程中會產生PdM需求，產生PdM任務集合T={T1，T2，…，Ti，…，Tn}，在設備的周圍部署用K表示的邊緣服務器K={K1，K2，…，Ki，…，Kn}。當執行PdM任務時，任務需要向邊緣基站卸載，當設備Ni的全部任務Ti結束時，可認為一個PdM的結束。一個邊緣服務器可以表示為K={R，F}，其中：R為任務卸載方案；F為資源分配方案，記錄分配給邊緣服務器上的任務。

每個任務都可以卸載到附近的邊緣服務器上，但限制設備Ni一次只能提交一個任務Ki。任意任務Ti可以用5個項目來描述，T={D，c，λ，α，τ}，其中：D是任務T的數據大小；c表示T的處理密度；λ為任務上傳時的設備故障率;α為卸載決策變量，即卸載的數據量占任務Ti總數據量的比例。α=0時，任務T局部處理，若α=1，任務T將被完全卸載。此外，大小為αD的數據將被卸載到邊緣服務器，（1-α）D的數據將被本地處理。τ為處理結果的數據大小與Ti的數據大小之比［10］。PdM的執行延遲是指從初始子任務開始到最后一個子任務結束的時間。我們采用一種非搶占式的任務調度策略，即只要一個子任務沒有完成，它的執行就不會被中斷。

本地計算的核心數為g1，β表示為可并行部分，分配給本地計算的每個核心的處理能力為fl。本地將計算（1-α）D比特數據的任務，包括串行部分tls=c（1-β）（1-α）D/fl和可并行部分tlp=cβ（1-α）D/flg1，則本地計算時間可以表達為

tl=tls+tlp=c（1-α）Dfl（1-β+βg1）。（1）

通過以上分析，可以得到αD位數據到邊緣的傳輸延遲。將αD位的數據卸載后，由邊緣服務器處理數據。用g2表示分配給邊緣處理任務的核數，設fe表示邊緣服務器每個核的處理能力（fefl），可串行部分表示為tes=c（1-β）αD/fe，可并行部分表示為tep=cβαD/feg2，邊緣計算時間可以表示為

te=tes+tep=cαDfe（1-β+βg2）。（2）

任務Ti的數據可以通過無線通信鏈路卸載到邊緣。對于數據傳輸速率，用r1表示。根據上述分析，αD位數據卸載到邊緣的傳輸延時表示為

tup=αDr1，（3）

則分配到邊緣計算的總耗時為

toff=te+tup。（4）

任務Ti處理完畢后，將結果返回給終端設備。取r2為返回結果過程中的數據傳輸速率，與卸載數據速率相似。根據上面的分析，τD結果返回的傳輸延遲可以表示為

tdown=τDr2。（5）

由以上分析可知，處理任務Ti的總延遲是本地計算時間、邊緣計算時間、卸載傳輸延遲和返回結果傳輸延遲的組合，且邊緣計算和本地計算同時進行，則總延遲公式可表示為

td=m864ff261324bfcebe0ff2e478c50f1957b029037fa6d8b1048fbb7a40821ec6fax{tl，te}+tup+tdown。（6）

1.2 維護成本模型

1） 設備故障率模型 我們假設λ為任務在t時刻的故障率，ak為壽命降低因子，bk為故障率增加因子（0<ak<1，0<bk<1）。離散隨機變量tk表示從上次實現預測性維護到下一次實現的累計運行時間，設備進行第k次預測性維護后的故障率可表示為分段連續變量［11］，

λk+1（t）=bkλk（t+aktk）。（7）

故障率在初始狀態λ1（t）的變化趨勢可以通過測試數據得到。故障率的變化隨著預測性維護的周期進行，任務的卸載權重會發生變化，任務權重將會影響任務的卸載順序。

2） 維護成本 當設備發生故障進行維護活動時的成本表示為糾正性更換成本（Cc），我們假設在PdM中涉及的糾正性維修成本為C［1］，

C=Cc（∑Mk=1∫tk0λkdt+∫ε0λM+1dt），（8）

其中：ε表示從上一次PdM活動到計劃生產周期P結束的剩余時間。一個預測性維護周期包括維護時間與延遲時間，M表示計劃生產周期P中PdM的循環次數，M=P/（td+tp）。

1.3 問題描述

我們提出了延遲軟約束的任務計算資源分配問題。給定一組設備N及其產生的任務T，優化問題定義為

min{∑NR，FC}， i∈N。（9）

上述優化問題主要通過調整任務卸載方案R和資源分配方案F，使所有設備的維護成本最小化。公式（10）約束卸載的總計算時間必須小于任務全部在本地的計算時間，

ti（te，te+tl）≤tli，i∈N。（10）

公式（11）限制分配到Ti的計算資源之和不大于邊緣服務器的可用總計算能力，

∑ni=1fli≤F，Ti∈T，Ki∈K。（11）

公式（12）、（13）約束每次進行計算的n個預測任務的數據大小不能超過邊緣服務器的總存儲空間，且邊緣服務器處理任務時應緩存任務所需的資源，

∑ni=1（1-α）D≤Γ，Ti∈T，Ki∈K，（12）

∑ni=1（1-α）（1-β）D≤Γ，Ti∈T，Ki∈K。（13）

我們將通過類比多重背包問題（multiple knapsack problem，MKP）證明我們提出的計算卸載和資源調度問題是NP-hard。多重背包問題的一個實例是將一組表示為{x1，…，xn}的n個任務分配給一組表示為{y1，…，yn}的m個不同背包，其中每個任務xi的相關利潤vi>0，權重wi>0，背包yi的容量為Wj。MKP是在不超過每個背包容量的情況下，選擇m個不相交的物品子集，使所選物品的總利潤最大化。本文所提問題類似于多重背包問題，任務xi可以被切分成兩部分：卸載計算和本地計算，卸載比率為α。根據需求二次把本地計算的任務卸載到邊緣，以獲得更大的計算效率。類比于背包問題，可證明此問題是NP-hard。1） 任務T={T1，T2，…，Ti，…，Tn}可以對應多重背包問題中的{x1，…，xn}。2） 權重wi>0可以對應卸載任務中的故障因子λ。3） m個不同背包的{y1，…，yn}類似于邊緣可提供的計算資源量。背包容積Wj為計算資源上限。

2 延遲軟約束的G2ABC算法

啟發式算法在實踐中被廣泛應用于解決NP-hard問題。文獻［12-13］改進貪心思想結合啟發式算法來解決NP-hard問題。文獻［14］共同研究了邊緣服務器布置和應用分配問題，提出了一種基于局部搜索的啟發式算法來有效解決該問題。由于容易陷入局部最優解，并不適合解決PdM問題，因此我們用多種啟發式算法，利用遺傳算法（GA）和人工蜂群算法（ABC）的優點從全局提出了一種基于GA-ABC算法的卸載和資源分配方法（G2ABC）。此算法包括兩部分：1） 算法將為每個任務選擇計算邊緣節點；2） 算法將決定邊緣節點的多少資源分配給任務。提出的算法主要關注獲得更低的維護成本、更高的資源利用率。

2.1 任務卸載算法

ABC算法是一種能夠擺脫局部最小值的優化技術，可以有效地用于模擬蜜蜂覓食行為的多變量、多模態函數 ［15］。在ABC算法中，人工蜜蜂的蜂群包含三組蜜蜂：雇傭蜜蜂、旁觀蜂和偵察兵。在跳舞區等待決定選擇食物來源的蜜蜂被稱為旁觀蜂，而前往自己之前訪問過食物來源的蜜蜂被稱為雇傭蜜蜂，進行隨機搜索的蜜蜂被稱為偵察蜂。ABC算法多用于調度問題，例如文獻［16］利用改進的人工蜂群算法解決無人機航跡規劃問題，加快了求解航跡的收斂速度，提高了航跡規劃效率和穩定性。

在ABC算法中，食物來源的位置代表了優化問題的一個可能解，食物來源的花蜜量對應于相關解的質量（適應度）。ABC生成隨機分布的初始種群P（G=0）的SN解（食物來源位置），其中SN表示種群大小。每個食物來源是一個E維向量，其中E為優化參數個數。初始化后，位置（解）的填充被反復循環，B=1，2，…，Bmax，表示雇傭蜜蜂、旁觀蜂和偵察蜂的搜索過程。雇傭蜂或旁觀蜂在尋找新的食物來源時，會對記憶中的位置進行修正，并測試新來源的花蜜量（適合度值）［17］。

遺傳算法在由基因和適應度函數組成的類染色體數據結構上進行遺傳表示，初始化一個解種群，然后依靠生物啟發的算子（如突變、交叉和選擇）對其進行改進。

利用上述算法優點，提出一個改進ABC算法的任務卸載方案。借鑒遺傳算法的思想，對ABC算法中偵察蜂的搜索過程進行改進，其中修改的部分如下。

1） 食物源 食物源表示為FS=<O，Z，C>，其中：O表示任務卸載方案；Z表示資源分配方案；C為PdM過程對應任務卸載和資源分配方案下的總成本。我們將FS的總集合表示為FSA ［18］，目的是為任務T在邊緣服務器上找到一個合適的卸載與分配方案，使得C最小化。

2）雇傭蜂階段 雇傭蜂從周圍尋找食物并記錄。為了從舊的蜜源獲得一個新的蜜源，ABC算法表達為

vij=xij+ij（xij-xkj）。（14）

3） 圍觀蜂階段 旁觀蜂選擇食物源取決于與該食物源相關的概率值pi，計算為

pi=fiti∑SNn=1fitn，（15）

式中：fiti為溶液i被雇傭蜜蜂評價的適應度值，該適應度值與雇傭蜜蜂位置i處食物源的花蜜量成正比；SN為食物源數量，等于雇傭蜜蜂數量（BN）。通過這種方式，雇傭蜂與旁觀蜂交換信息。

4） 偵察蜂階段 在ABC中，當原食物源在預定周期內無法產生更優解時，部分蜂群會轉變為偵察蜂去隨機尋找新的食物來源。為了避免過快收斂以及陷入局部最優解，我們參考了遺傳算法的交叉變異運算，并能在未知方向尋找更好的解，利用遺傳算法的變異過程重新尋找蜂源，從而可以更好地搜索解空間。

根據上述描述，G2ABC算法具體步驟如下。

算法1 G2ABC

輸入： 食物源的數量SN，維護任務T，邊緣節點K。

輸出：任務卸載方案O，資源分配方案Z。

1） FSA=0，初始化輪數cycle

2） for i=1：SN

3） 為每一個任務隨機分配一個邊緣節點K，將卸載方案表示為O

4） 算法5得到初始資源分配方案Z

5） FS=<O，Z，C>

6） FSA=FS

7） end for

8） while j<cycle

9） 調用算法2

10） 調用算法3

11） 調用算法4

12） end while

13） FS=FSbest

算法1說明了G2ABC的細節。在第一行將種群設置為空完成初始化。首先將種群初始化，隨后對種群進行初始化。根據算法5得到最初的分配方案。隨后進行輪轉搜索。

算法2 雇傭蜂算法

輸入： 食物源FSA，維護任務T，邊緣節點K。

輸出： 更新的食物源FS。

1） for FSi∈FSA

2） 隨機選擇食物源j，FSj∈FSA

3） FSj.O使用算法5更新新的食物源FSj

4） 根據公式（14）得到食物源FSm

5） FSm.O使用算法5更新新的食物源FSm

6） FS=FSm

7） end for

算法2是雇傭蜂詳細過程。對于種群中的每個食物源，根據公式（14）搜索，并生成新的食物源。

算法3 圍觀蜂算法

輸入： 食物源FSA，維護任務T，邊緣節點K。

輸出： 更新的食物源FS。

1） 根據式（15）概率選擇FSj，FSj∈FSA

2） 根據公式（14）得到食物源 FSm

3） FSm.O使用算法4更新新的食物源FSm

4） 對比FSm、FSj更新最優食物源FSbest

算法3介紹了圍觀蜂的過程。旁觀蜂和雇傭蜂的過程相似，根據輪盤對賭搜索出最佳食物源，然后更新最優食物源。

算法4 偵察蜂算法

輸入： 食物源FSA，維護任務T，邊緣節點K。

輸出： 更新的食物源FS。

1） forFSi∈FSA

2） if有偵察蜂出現

3） FSi.O使用交叉變異生成新的FSj.O

4） FSm.O使用算法5更新新的食物源FSm

5） end if

6） 更新食物源 FSi=FSm

7） end for

算法4是基于GA優化的偵察蜂算法。當有偵察蜂出現的時候，步驟2）根據交叉變異形成新的食物源跳脫出原有解，防止陷入局部最優。

2.2 資源分配算法

在PdM活動中，生產設備由于磨損而不斷退化，故障率不斷上升，合格率不斷下降。定義卸載返回后的故障率作為輔助變量集Λ，定義中間變量

yi=λi/fli（16）

為故障率和分配資源的比值，可以反映資源分配的質量。算法需要優先對故障率高的任務分配資源，通過調整資源分配方案，使每個任務的中間向量值趨于統一。

算法借鑒了二分搜索的思想，在公式（11）的約束內找到一個資源分配方案，使得最終的設備維護成本最小［12］，具體算法流程如下。

算法5 故障優先資源分配算法

輸入： 任務卸載方案O，邊緣節點K，維護任務T。

輸出： 資源分配方案Z。

1） for Ki∈K

2） 將Ki上的任務定義為Tres

3） for Ti∈Tres

4） 平均分配計算資源，根據式（16）得到集合Λ

5） ymin=min｛Λi｝，ymax=max｛Λi｝

Y=（ymin+ymax）/2

6） while （y-ymin>0）

7） if 分配的計算資源大于總資源

8） ymax=y

9） else if 分配的計算資源小于總資源

10） ymin=y

11） end if

12） y=（ymin+ymax）/2

13） end while

14） 根據式（16）得到重新分配的計算資源

15） end for

16） end for

17） 將得出的資源分配方案賦值給F

18） return F

算法5根據式（16）對任務進行初始資源分配，并且設定了上、下限。利用二分搜索，在設定計算資源范圍內找到合適的值，并對任務重新分配資源。

3 仿真驗證與分析

首先介紹實驗中的設置和比較算法，然后討論評價結果。

根據文獻［19-20］，將邊緣服務器的通信范圍設置為500m，邊緣服務器計算資源設置為1×109 CPU周期/s，本地計算資源設置為1×104 CPU周期/s。為了對比不同算法之間的性能，將任務數設置為20、40、60和80個，計算資源分別設置為1×109、2×109、3×109和4×109 CPU周期/s。

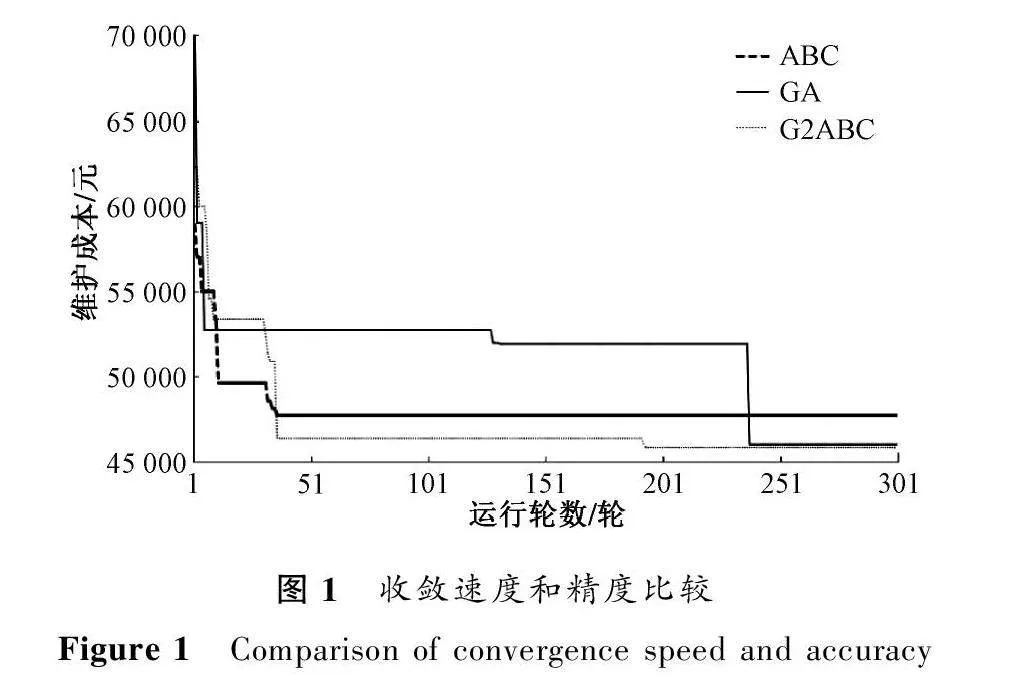
1） 收斂性能。選擇基于ABC的任務卸載算法和基于GA的任務卸載算法與G2ABC進行比較。所有的算法都使用統一的資源分配算法。

從圖1中我們可以看出G2ABC算法和ABC算法在收斂速度上優于GA算法，且G2ABC算法在進化策略影響下，200次迭代后的維護成本顯著小于其他算法。這意味著G2ABC可以快速準確找到任務卸載方案。

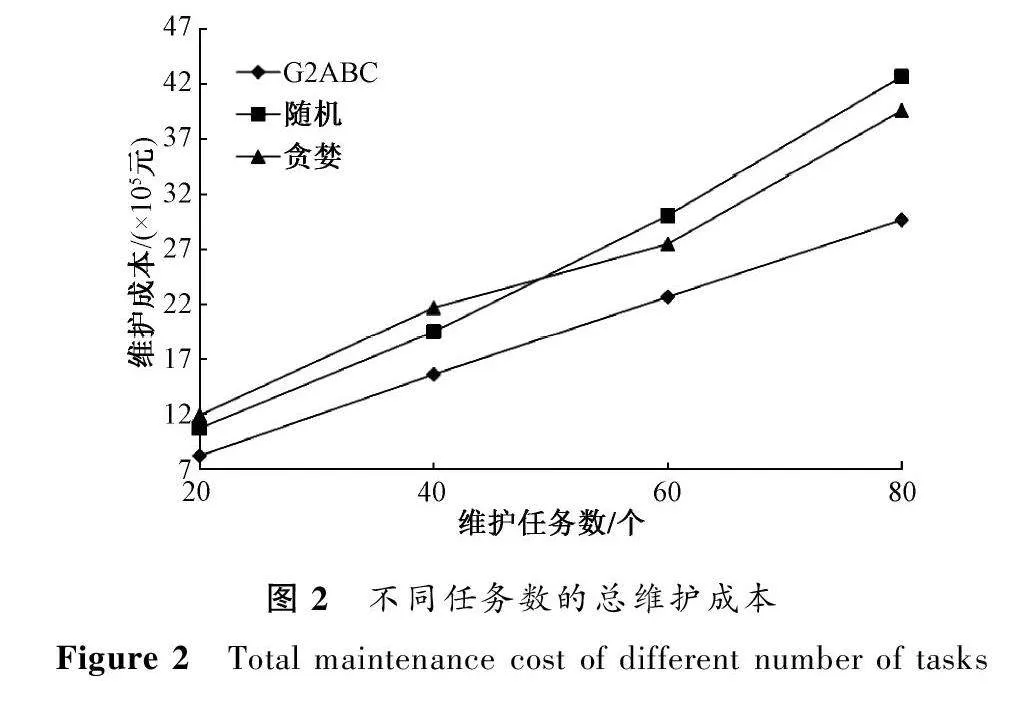
2） 所有任務的總維護成本。為了顯示G2ABC算法適用問題，與隨機分配算法和貪婪算法進行比較。

圖2顯示了不同算法在任務數量不同時的維護成本趨勢，三種算法的結果都隨著任務數的增加而增加。隨機算法在任務數40之前的維護成本優于貪婪算法，而隨著任務數增加，貪婪算法的維護成本逐漸優于隨機算法。對比兩種算法，G2ABC可以保持較低的成本損耗，即G2ABC算法可以得到成本相對最小的資源分配方案。

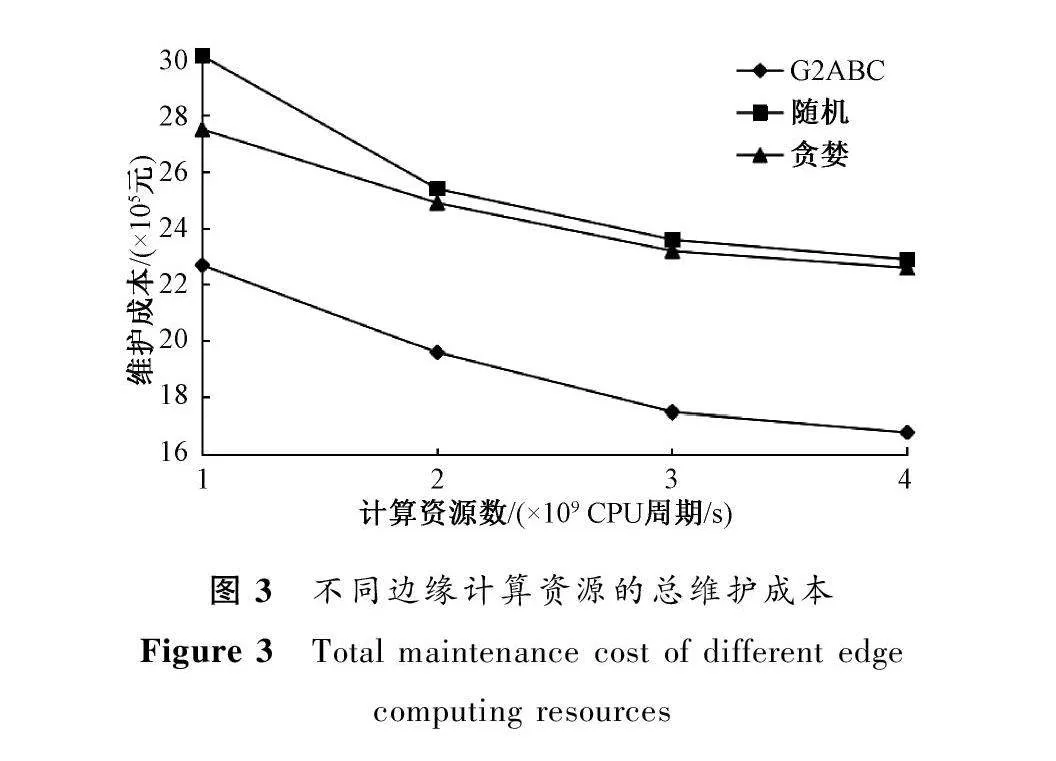
3） 不同計算資源下的對比。為了對比不同算法在不同計算資源下的性能，將維護任務數設置為60。

圖3顯示了不同算法在邊緣服務器計算資源不同時的維護成本趨勢，三種算法的結果都隨著資源數的增加而減少。由于計算資源的增多，可供任務使用的計算資源增加，計算時間變少，從而維護成本變低。以資源數為3×109 CPU周期/s為例，貪婪算法和隨機算法的維護成本值分別為232萬元和236萬元，本文算法的維護成本為175萬元，這說明本文算法在此情況下可得到更少的維護成本。且在不同邊緣計算資源數下均有較好的維護成本。

4 結論

在本文中，我們對預測性維護的計算卸載和資源分配問題進行全面的數學建模，并且證明此問題是NP-hard的。為了解決這一問題，本文提出了一種G2ABC算法，算法對延遲時間進行軟約束，以減少設備的維護支出為目標，找到合適的任務卸載和資源分配方案。通過實驗表明，對比其他算法，我們的方法可以給出一個合適的任務卸載和資源分配方案，減少了預測性維護成本。

參考文獻：

［1］ RAN Y Y， ZHOU X， LIN P F， et al. A survey of predictive maintenance： systems， purposes and approaches［EB/OL］. （2019-12-12）［2022-10-16］. https：∥arxiv.org/abs/1912.07383.

［2］ ZHAO R， YAN R Q， CHEN Z H， et al. Deep learning and its applications to machine health monitoring［J］. Mechanical systems and signal processing， 2019， 115： 213-237.

［3］ KHAN S， YAIRI T. A review on the application of deep learning in system health management［J］. Mechanical systems and signal processing， 2018， 107： 241-265.

［4］ TRAN T X， HAJISAMI A， PANDEY P， et al. Collaborative mobile edge computing in 5G networks： new paradigms， scenarios， and challenges［J］. IEEE communications magazine， 2017， 55（4）： 54-61.

［5］ MACH P， BECVAR Z. Mobile edge computing： a survey on architecture and computation offloading［J］. IEEE communications surveys & tutorials， 2017， 19（3）： 1628-1656.

［6］ 田釗， 王超， 賈駿， 等. 基于局部自組網的路況信息可靠共享模型［J］. 鄭州大學學報（理學版）， 2022， 54（6）： 82-90.

TIAN Z， WANG C， JIA J， et al. A reliable traffic information sharing model based on local-VANET［J］. Journal of Zhengzhou university （natural science edition）， 2022， 54（6）： 82-90.

［7］ DENG Y Q， CHEN Z G， CHEN X H. Resource allocation for multi-user mobile-edge computing systems with delay constraints［C］∥IEEE Global Communications Conference. Piscataway： IEEE Press， 2021： 1-6.

［8］ AHMED I， YAN S， RAWAT D B， et al. Dynamic resource allocation for IRS assisted energy harvesting systems with statistical delay constraint［J］. IEEE transactions on vehicular technology， 2022， 71（2）： 2158-2163.

［9］ HORIMOTO S， HE F J， OKI E. Delay-aware backup resource allocation with probabilistic protection for network services［C］∥IEEE 22nd International Conference on High Performance Switching and Routing. Piscataway： IEEE Press， 2021： 1-6.

［10］KIANI A， ANSARI N， KHREISHAH A. Hierarchical capacity provisioning for fog computing［J］. IEEE/ACM transactions on networking， 2019， 27（3）： 962-971.

［11］LI D F， HONG P L， XUE K P， et al. Virtual network function placement and resource optimization in NFV and edge computing enabled networks［J］. Computer networks， 2019， 152： 12-24.

［12］DINH T Q， TANG J H， LA Q D， et al. Offloading in mobile edge computing： task allocation and computational frequency scaling［J］. IEEE transactions on communications， 2017， 65（8）： 3571-3584.

［13］LUO Q Y， HU S H， LI C L， et al. Resource scheduling in edge computing： a survey［J］. IEEE communications surveys & tutorials， 2021， 23（4）： 2131-2165.

［14］HE Y H， HAN X， GU C C， et al. Cost-oriented predictive maintenance based on mission reliability state for cyber manufacturing systems［EB/OL］. （2018-01-12） ［2022-12-16］. https：∥doi.org/10.1177/1687814017751467.

［15］劉倩雯. 人工蜂群算法及其在調度問題中的應用研究［D］. 北京： 北京交通大學.

LIU Q W. Artificial bee colony algorithm and its application in scheduling problem［D］. Beijing： Beijing Jiaotong University.

［16］劉琨， 封碩. 面向無人機航跡規劃的改進人工蜂群算法［J］. 鄭州大學學報（理學版）， 2021， 53（1）： 74-79， 126.

LIU K， FENG S. Improved artificial bee colony algorithm for UAV path planning［J］. Journal of Zhengzhou university （natural science edition）， 2021， 53（1）： 74-79， 126.

［17］KARABOGA D， BASTURK B. A powerful and efficient algorithm for numerical function optimization： artificial bee colony （ABC） algorithm［J］. Journal of global optimization， 2007， 39（3）： 459-471.

［18］ZHOU J Y， ZHANG X L. Fairness-aware task offloading and resource allocation in cooperative mobile-edge computing［J］. IEEE Internet of Things journal， 2022， 9（5）： 3812-3824.

［19］HE Y H， REN J K， YU G D， et al. D2D communications meet mobile edge computing for enhanced computation capacity in cellular networks［J］. IEEE transactions on wireless communications， 2019， 18（3）： 1750-1763.

［20］PARVEZ I， RAHMATI A， GUVENC I， et al. A survey on low latency towards 5G： ran， core network and caching solutions［J］. IEEE communications surveys & tutorials， 2018， 20（4）： 3098-3130.