基于優化模糊PID控制器的精準施肥算法研究與應用

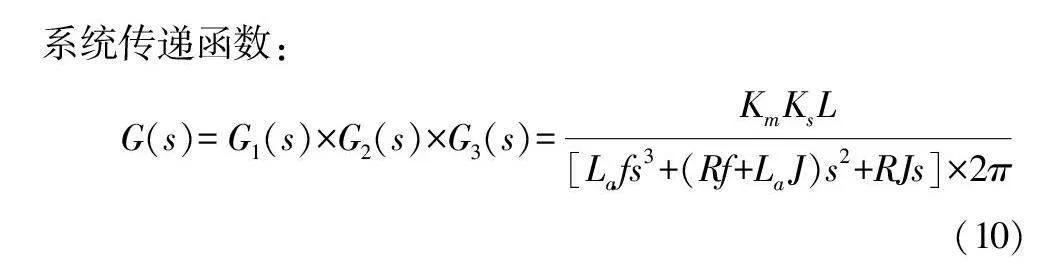
摘要 針對農業生產灌溉施肥過程中水肥施用精度不高，造成資源浪費、土壤板制化的問題，該研究設計了一種基于粒子群優化（PSO）的模糊PID 算法控制施肥機的灌溉施肥過程。首先，針對施肥的相關模塊以及相應參數，建立施肥機數學模型。然而，基于MATLAB/Simulink平臺分別搭建PID控制器、模糊PID控制器以及該文提出的控制器，對建立的系統數學模型進行了控制。仿真結果表明，該控制算法響應時間縮短至30 s，相較于PID、模糊PID分別縮短了63.4%和55.9%。該控制算法除了前期震蕩外，基本不存在超調量。為了驗證該算法在實際應用中的可靠性，設計了不同壓強下的精度控制試驗。結果表明，基于PSO優化的模糊PID控制器在各個壓強下都具有良好的控制效果，控制精度在2%左右，而PID控制器的控制精度在20%左右，模糊PID控制器的控制精度在10%左右。由此可見，該研究提出的控制算法在實際應用過程中能夠提升灌溉精度。

關鍵詞 水肥一體化；模糊控制；復合控制；實驗驗證

中圖分類號 S232.3 文獻標識碼 A 文章編號 0517-6611（2024）15-0203-05

doi：10.3969/j.issn.0517-6611.2024.15.043

開放科學（資源服務）標識碼（OSID）：

Research and Application of Precise Fertilization Algorithm Based on Optimal Fuzzy PID Controller

LI Huai-sheng， CUI Yu

（Institute of Agricultural Science（Institute of Animal Science），9th Division of Xinjiang Production and Construction Corps，Emin，Xinjiang 834601）

Abstract In the process of irrigation and fertilization in agricultural production，the application accuracy of water and fertilizer is not high，resulting in resource waste and soil plate formation.In this study，a fuzzy PID algorithm based on PSO optimization was designed to control the irrigation and fertilization process of the fertilizer applicator.Firstly，the mathematical model of fertilizer applicator was established according to the relevant modules and parameters of fertilization.Based on MATLAB/Simulink platform，PID controller，fuzzy PID controller and the controller proposed in this paper were built respectively to control the mathematical model of the established system.The simulation results showed that the response time of the proposed control algorithm was reduced to 30 s，which was reduced by 63.4% and 55.9% respectively compared with PID and fuzzy PID.In terms of overshoot，there was basically no overshoot in the proposed control algorithm except for the early oscillation.In order to verify the reliability of the algorithm in practical application，this paper designed precision control tests under different five groups of pressures，and the test results showed that the fuzzy PID control based on PSO optimization had good control effect under various pressures.The control accuracy was concentrated in about 2%，while the control accuracy of PID control was about 20%，and the control accuracy of fuzzy PID control was about 10%.It could be seen that the control algorithm proposed in this study could improve the irrigation accuracy in the practical application process.

Key words Integration of water and fertilizer;Fuzzy control;Compound control;Test verification

水肥的不均衡施加容易造成土壤的板制化以及農作物的減產［1］。精準施肥控制逐漸成為目前水肥控制的重要發展趨勢［2］。在植物生長過程中，調節植物對施用量的需求是目前農作物生產的重要內容。流量控制過程需要考慮指標延遲等因素，宏觀上講，水肥一體化灌溉施肥過程中流量值的調節存在嚴重的時變性、非線性及遲滯性，給水肥的調節過程帶來一定的難度。目前水肥一體化的研究主要集中在控制算法及數學模型2個方面［3］。精確的數學模型有利于分析施肥機施肥過程中的各項性能指標，也為接下來的控制提供必要的精準性。數字模型的建立，需要先進的控制算法來調控灌溉施肥過程［4-5］。

若以水肥一體化控制過程中的各項特性作為控制優化的目標，傳統的PID控制已經不能滿足調控過程中的指標需求。在考慮施肥系統遲滯性的前提下，劉艷妮等［6］提出一種參數自適應調整的Fuzzy-PID控制方法，該方法對模型精準性需求不高，但容易陷入死區。針對不同隸屬度函數的設定與需求，提出一種新型的模糊控制規則，該研究設計了對筆者提出算法的驗證分析，結果表明：相較于傳統的控制方式，該控制方式超調量減少32%，調節時間縮短90 s。彭娜等［7］建立了灰色預測模型，重點研究了灌溉過程中肥料的施用和模糊PID控制的實施。在灰色預測的基礎上，對水、肥泵的轉速進行了模糊PID控制?？紤]到血球藻液流量值控制系統的許多缺點，比如非線性、時變性、嚴重滯后性和不確定數學模型等，全彥濤等［8］提出了一種基于模糊PID的流量控制方法。目前模糊PID算法的研究已相對成熟。這種算法既可以滿足模糊控制快速調節的特性，又可以實現PID相對精準的控制作用。然而，模糊PID算法對PID算法的優化效果較差，因此需要提出新型的參數調節算法。

相關研究人員集中研究了基于算法優化的模糊PID控制。大量的優化算法已經被提出，比如遺傳算法、著名的神經網絡算法和蟻群算法［9-10］。參數調整的優化主要包括2個方面的考慮：一是尋求全局最小點，二是要有很好的收斂速度。神經網絡算法目前主要被應用于PID控制領域，其優點是可以按梯度下降方向優化到局部最小點，進而獲得更有利的控制。李冬冬等［11］通過神經網絡預測控制和模糊控制對時變非線性模型的動態管理控制系統達到更精確的控制。但是，神經網絡算法的缺點是容易陷入局部最小值；此外，遺傳算法需要進行編碼輸出和解碼設計，在某些情況下這些都是極其困難的，不能直接進行并行處理，計算量極其龐大。然而，粒子群優化（PSO）不具備遺傳算法的編碼和解碼交叉、變異和設計過程的復雜思想，沒有梯度信息，運行效率較快，實施方便，收斂迅速?；赑SO優化的PID控制是一種思想較為樸素、實用的新型整定方法，大大提升了PID 3個參數的優化水平，優化后控制系統的性能指標大幅度提升，在工業領域具有巨大的潛在價值［12-14］。

目前提出了一種改進的模糊PID控制器，根據誤差范圍來確定控制方法的選擇，有效利用PSO來優化模糊控制器的3個比例參數。

在MATLAB/Simulink平臺上進行仿真驗證，通過比較PID控制算法、模糊控制算法、模糊PID控制算法和該文提出的控制算法，發現該研究所提出算法的性能指標優于其他控制算法。

為了驗證該文所提出的算法投入生產實踐的可靠性，筆者設計了相關試驗，通過數據采集、讀入主機、傳遞信號和提供決策指令來實現。

1 控制系統數學模型的建立

該系統的流量調節裝置為電動比例閥，電動比例閥由驅動電機以及閥體組成。電機通過轉動帶動傳動部分，從而對閥芯進行控制，從而實現對閥體的開度控制。電動比例閥實現對開度的控制，從而形成對流量的控制。電動比例閥由直流電機、調速器、數據采集檢測模塊、上位機控制器組成。直流電機：此裝置通過接收上位機閥門開度電信號，由脈沖寬度調制技術（PWM）進行脈寬調制輸出、控制脈沖，控制電機的正轉或者反轉以及時長，從而實現對閥門開度的增大或減小。

直流電機需要通過直流的驅動進行正常工作，所以需要將交流經過逆變形成直流電壓。

電機對閥門閥芯的操作需要通過傳動部分間接控制，傳動部分由減速裝置實現電機的轉速控制，并提高輸出的轉矩，通過轉桿的傳動可將電機旋轉的角位移轉換為直線位移。

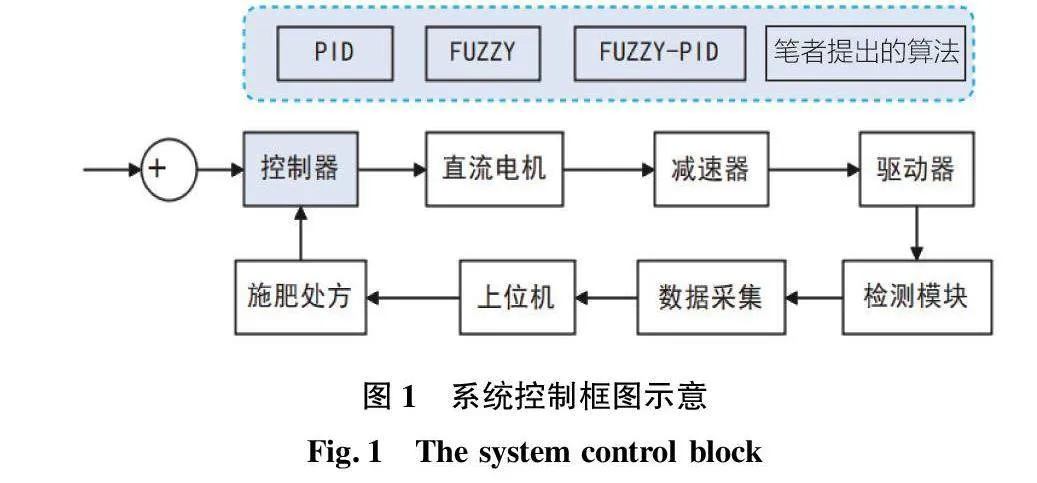
控制部分由控制終端微控制單元（MCU）以及控制盒組成。MCU是實現控制算法的關鍵器件，而控制盒則可根據 PWM 信號控制開關的通斷，通過輸出電機的驅動電壓控制電機的轉速、正反轉及啟停。 電動比例閥的控制采用閉環控制的策略，通過位置輸入信號由控制器形成決策信號，通過調整電壓的輸出并驅動電機進行啟停、正反轉，電機對閥芯進行傳動從而改變閥門開度的大小。位置傳感器的作用是通過檢測閥門開度信息，將其傳輸給控制器，從而形成一個閉環控制。系統控制原理框圖如圖1所示。

通過對液肥噴施變量控制系統控制部分電動比例閥的構成分析，傳遞函數由直流電機、減速裝置、電壓驅動構成電動比例閥開度控制。

直流電機傳遞函數：

直流電機是電動比例閥中的驅動裝置，直流電機由于控制的高精度、容易控制的特點，在調速控制及正反轉領域得到了廣泛應用。電機轉速及行程控制關系到閥控的精準操作，直流電機的電壓與行程的傳遞函數推導過程如下。電機驅動電壓的平衡方程式如下：

Ud（t）=RId+LdId（t）dt+E（t）（1）

其中，Ud（t）為直流電機的驅動電壓，R為內阻，Id（t）為電驅電流，E（t）為電動勢。

輸出轉矩的計算公式可表示如下：

M（t）=KId（t）（2）

式中，M（t）為直流電機輸出的轉矩，K為直流電機力矩系數。

直流電機轉矩表達式如下：

M（t）-M1（t）=Jdw（t）dt（3）

式中，M（t）為負載的力矩，J 為直流電機的轉動慣性量，w（t）為直流電機的轉速。

M1（t）=fθ··（t）（4）

其中， f為摩擦系數，θ為電機輸出的轉角。聯立上述公式，可得：

Id（t）=1Km［Jθ·（t）+fθ··（t）］（5）

將上式帶入電壓平衡方程，可得：

LJ θ···（t）+（Lf+RJ）θ·（t）+Rf θ··（t）+KmEm（t）=KmU（t）（6）

其中，Km為反電動勢系數。經過拉普拉斯反變換，可以得到直流電機輸出轉角與輸入電壓的傳遞函數：

G1（s）=θ（s）U（s）=KmLafs3+（Rf+LaJ）s2+RJs（7）

根據各部分之間的串聯關系，將輸出轉角作為減速裝置的輸入參考，通過降低電機轉速來提高輸出轉矩，其表達式為減速裝置轉矩與直流電機輸出轉矩之比。將該環節等效為2個轉角之間的比例關系，則該部分的傳遞函數為2個轉角之間的比例關系，可反映減速裝置的輸出位移與輸入轉角的關系，可列出下式：

G2（s）=X（s）θ（s）=L2π（8）

其中，L表示導桿的導程，X為輸出位移。

通過上述2個環節的建模，施肥機驅動部分的傳遞函數可以由輸出電壓與輸入電壓計算得到。此外，該傳輸模塊存在一定的延遲，延遲時間相較于開關頻率可以忽略。綜上，此電壓驅動模塊的傳遞函數如下：

G3（s）=Uout（s）Uin（s）=Kseτs≈Ks（9）

各模塊之間是并聯關系，Ks為變換器放大系數，可得到系統傳遞函數：

G（s）=G1（s）×G2（s）×G3（s）=KmKsL［Lafs3+（Rf+LaJ）s2+RJs］×2π（10）

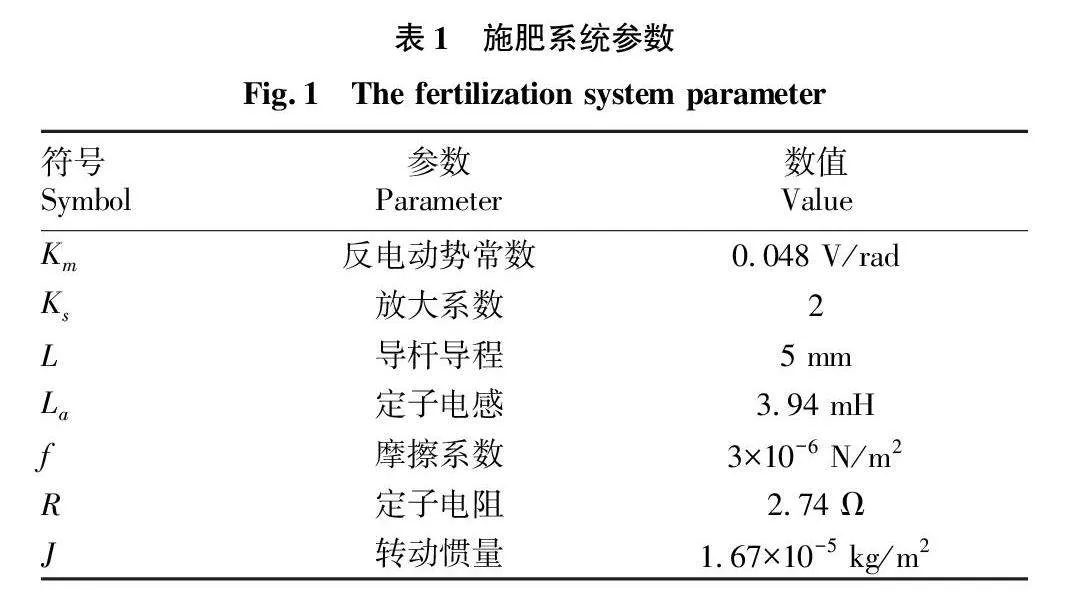
施肥系統參數如表1所示。

將參數帶入數學模型可得：

G（s）=0.0489.9×10-5×s3+4.65×10-4×s2+2.87×10-4×s（11）

2 模糊PID 控制器的設計

PID控制在滴灌田施肥系統接近平衡點時工作，設定的比例、積分、微分系數不易過大。將輸出的反饋值與設定的流量值作為該方法的追蹤誤差，通過3個參數對系統的調節，讓誤差盡可能在短時間內趨近于0。由于該研究的控制對象具有非線性、遲滯性等特點，不宜搭建數學模型。傳統的PID控制整定過程較為煩瑣，耗時長，超調量大，而且PID控制的3個參數不易于調節，控制效果差。

2.1 模糊控制器的設計

根據國家指定的灌溉施肥標準等文件，選定該研究的隸屬度函數以及模糊控制規則。選取混肥罐的流量值誤差E以及誤差倒數EC作為模糊控制的2個輸入變量，輸出變量確定為酸液罐控制閥的開度U。將2組輸入值通過縮放因子模糊化，通過設定的規則做出模糊決策，決策后的模糊量經過量化得到實際調制過程中酸液罐電磁閥的控制開度，間接推算酸堿液罐的通斷時間。量化因子分別設為kec和ke，比例因子設為ku。

En=bn-ba（12）

En-1=bn-1-ba（13）

ECn=En-En-1T=bn-bn-1T（14）

其中：ba 表示作物生長而設定的作物需求參考標定的流量值；bn、bn-1分別表示第n、n-1試驗的流量值；En-1、En分別為第n-1、n次試驗的流量值與設定值的偏差；ECn 表示第n次測試流量值偏差的變化率；T 表示試驗采樣時間。

設定隸屬度函數為三角形，根據模糊控制準則，相交模糊子集的交集閾值為0.2～0.7，這可以保證系統的穩定性與靈活性。

根據施肥控制的模糊經驗，該研究提到的誤差、誤差導數、控制率在隸屬函數的選擇上沒有特殊的必要性，該文采用三角隸屬函數作為研究對象。為了比較不同隸屬度函數對梯形隸屬度函數的影響，選擇高斯隸屬度和控制系統函數作為研究比較對象。

將流量值誤差E與誤差倒數EC的模糊語言均定義為對稱的7個模糊規則，即［NB，NM，NS，O，PS，PM，PB］，對應的模糊論域設定為［-3，-2，-1，0， 3］，模糊語言的定義由左向右依次為負大、負中、負小、0、正小、正中、正大。不同的語言組合反映不同的系統運行狀態，有利于系統進一步做出決策。如果誤差E為NB，說明混肥罐中的流量值遠小于植物需求值，其他同理。

為了控制簡易施肥過程，模糊輸出U定義為5個對稱的模糊語言，即為［NB，NS，O，PS，PB］，對應的模糊論域設定為［-4，-2，0，2，4］，從左到右依次解釋為酸堿液罐的通斷時間開通時間長、開通時間短、不開通、關斷時間短、關斷時間長。

將系統本身構建為閉環，經過分析得出系統流量值誤差，最大浮動在8左右。為了方便后續區間計算，將誤差論域定義為［-8，8］，同理流量值誤差倒數EC的基本論域為［-1.8，1.8］，酸液罐的電磁閥開通時間論域設定為［-8，8］。帶入模糊控制時，需要對三者進行量化與反比例，ke=0.375，kec=3/1.8=1.67，ku=8/4=2。

模糊規則共49條，每一條規則對應一種模糊決策。模糊規則的基本樣例為“如果E和EC，則U”。如果E是NB，EC是NB，那么U是NB，表明流量難以滿足植物需求，且變化率快速增長時酸液罐應保證長時間開通。

2.2 模糊-PID復合控制器的設計

結合PID控制的精準性與模糊控制的快速性，將二者結合控制系統的作業過程。將追蹤誤差e與設定誤差e0進行比較，當追蹤誤差大于設定誤差時采用模糊控制，讓追蹤誤差快速收斂至較小值，直到追蹤誤差小于等于給定誤差，采用PID控制，保證整個系統控制的精準性。這使得滴灌植物田間施肥系統既擁有良好的動態性能，又有低穩態誤差的優勢，彌補了模糊控制中平衡點附近死區的不足。

2.3 基于PSO優化的模糊PID控制器構建

肥料融合和傳感器檢測具有一定的時間滯后性，加上控制方案不確定性因素的影響和施肥過程中肥料配比的變化，用傳統的控制方法很難完成肥料控制效果和理想的水量。在普通模糊PID控制模型的基礎上，在目標損失函數中加入帶時間權重的粒子群優化目標函數，并將I、D和P設定為Ki、Kd和Kp。

為了更好地優化PID控制的補償參數，該研究將模擬仿生學中的粒子群體群居效應作為優化參數的方法。將粒子群引申為群居的鳥群等，其基本思想是通過個體對群體最優值的不斷探尋，最后將整個信息共享的群體均趨于最優值。

vij（t+1）=vij（t）+c1r1（t）［pij（t）-xij（t）］+c2r2（t）［pgj-xij（t）］（15）

事實上，空間向量也被定義成多維。假定每個粒子是無質量的個體，隨機的粒子在K維矢量中的位置表示為xi ={（xi1），（xi2），…，（xik）}，i = …，n。引入粒子群需要優化參數的代價性目標函數，計算每個粒子在尋優過程中的最優值，將所有信息更新后驗證適應性函數的優劣性。每個隨機粒子的速度表示為vi={（vi1），（vi2），…，（vik）}，結合粒子原來的信息，將粒子信息更新為pi={（pi1），（pi2），…，（pik）}，假定粒子信息更新至最優位置時的位置表示為pg={（pg1），（pg2），…，（pgk）}。由此，將個體更新的迭代方程推導如下。

xij（t+1）=xij（t）+vij（t+1）（16）

其中，i表示第i個粒子， j表示第j個維度的粒子，c2和c1為0～2的加速常數，r2和r1是2個均勻分布的獨立隨機函數。

上面的方程為粒子更新迭代的核心：即每個粒子當前所處的狀態信息，每個粒子的速度更新、位置更新。值得一提的是，這種更新信息的方式針對不同的問題有不同的方式，這主要取決于問題的3個方面信息：目標函數、變量組成以及約束條件。

參數優化的評定標準由自定義的目標函數作為反饋指標。不同目標函數的性能指標標準不同，對控制算法指導過程的優化難易程度也不同，因此方便計算且能滿足系統性能需求的函數是首選。該研究誤差絕對值的積分作為反饋該試驗的性能函數。

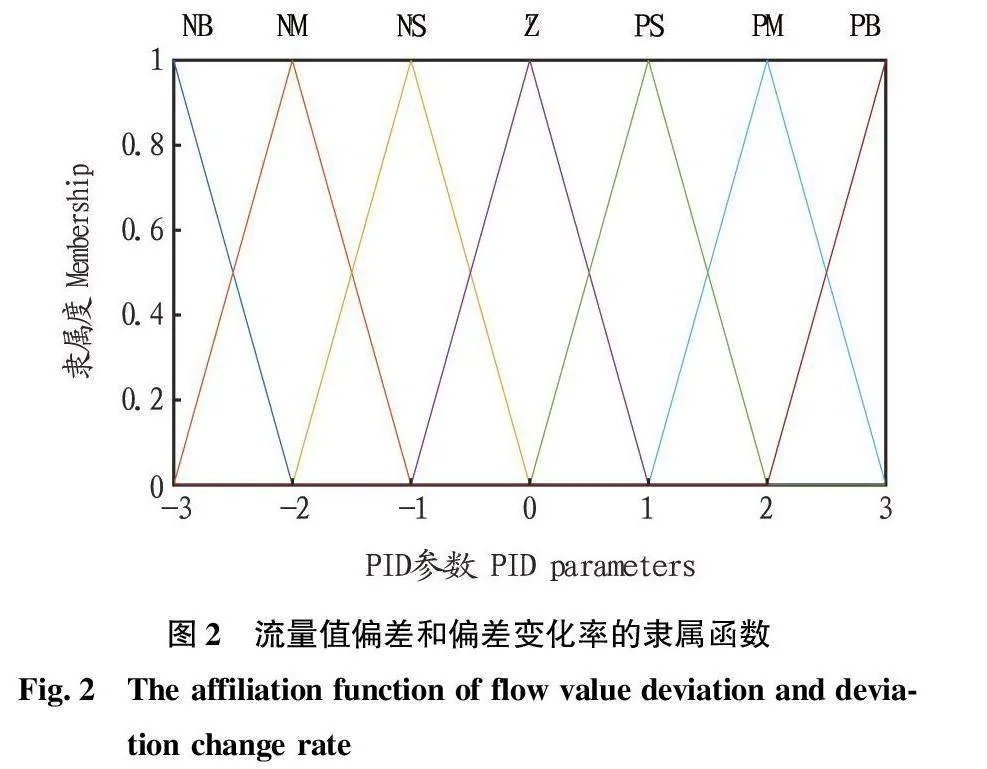
模糊算法設計如下：應用于輸出和輸入隸屬函數的形式為三角形，在解模糊方法上選擇區域重心法。流量值偏差E和流量值偏差變化率EC的語言值選擇為［NB，NM，NS，Z，PS，PM，PB］，模糊域為［-3，-2，-1，0， 3］。作為輸出的3個參數Kp、Kd和Ki對應的語言學值為［NB，NM，NS，Z，PS，PM，PB］，模糊域為［-3，-2，-1，0， 3］。

通過總結專家對植物生長適宜的肥料流量值經驗，選擇了“if ec and e then Kp、Kd and Ki”的模糊控制語句，由49個條件語句組成。

由Matlab的模糊推理系統隸屬度函數組成的水肥流量值偏差和偏差變化率的隸屬函數如圖2所示，水肥流量值模糊控制器輸出變量的隸屬函數如圖3所示。

3 肥料混合過程中水和肥料流量值控制的仿真研究

為了驗證提出算法的優越性，在MATLAB/Simulink平臺搭建了水肥一體機系統模型，分別建立4種不同的控制方式。外界的參數設置如下：試驗場地灌溉水的流量值為8，酸液罐中的稀鹽酸濃度為0.25 mol/L，灌溉水的流量為1.7 L/s，測定系統存在4 s延遲。

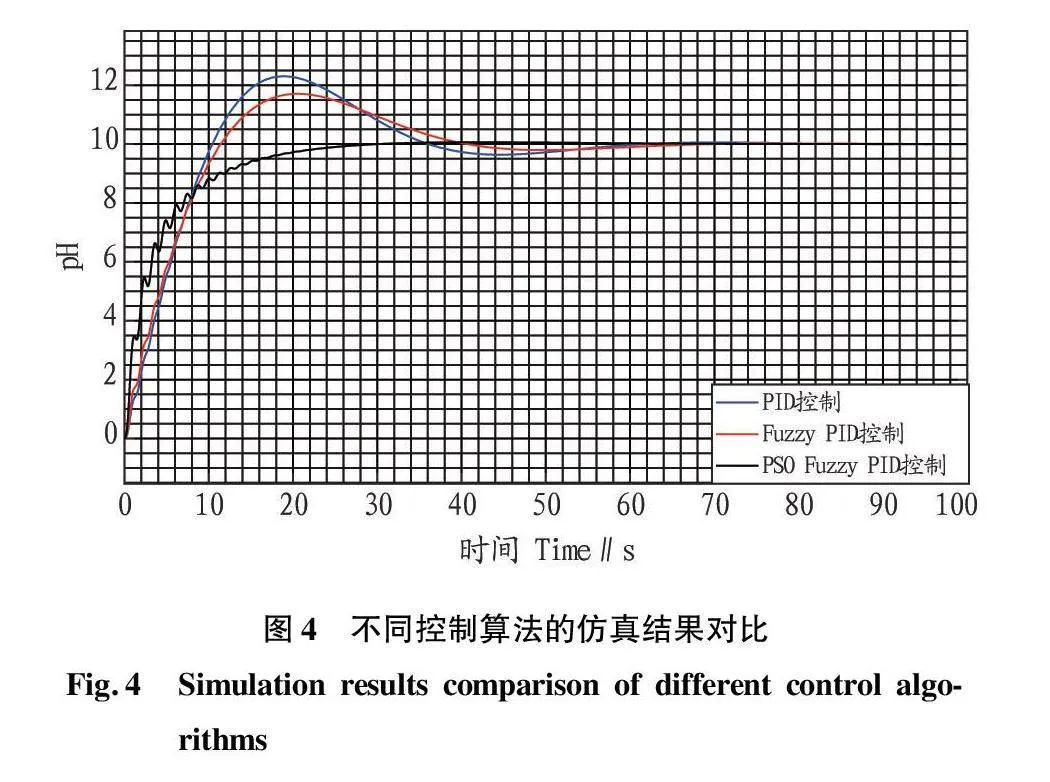
相關參數被帶入仿真模型，不同控制算法的跟蹤曲線如圖4所示。一般來說，以pH=8的參考信號為研究對象，通過繪制表格和跟蹤，提取不同控制方法的性能指標參數。該研究設計的控制策略與前2種算法相比，調節時間和上升時間有一定程度的下降，超調現象得到有效抑制，彌補了PID控制和模糊控制的不足，提高了施肥過程的準確性。從理論上講，通過這種復合控制器可以優化肥料和水的流量值調節。

4 實驗驗證

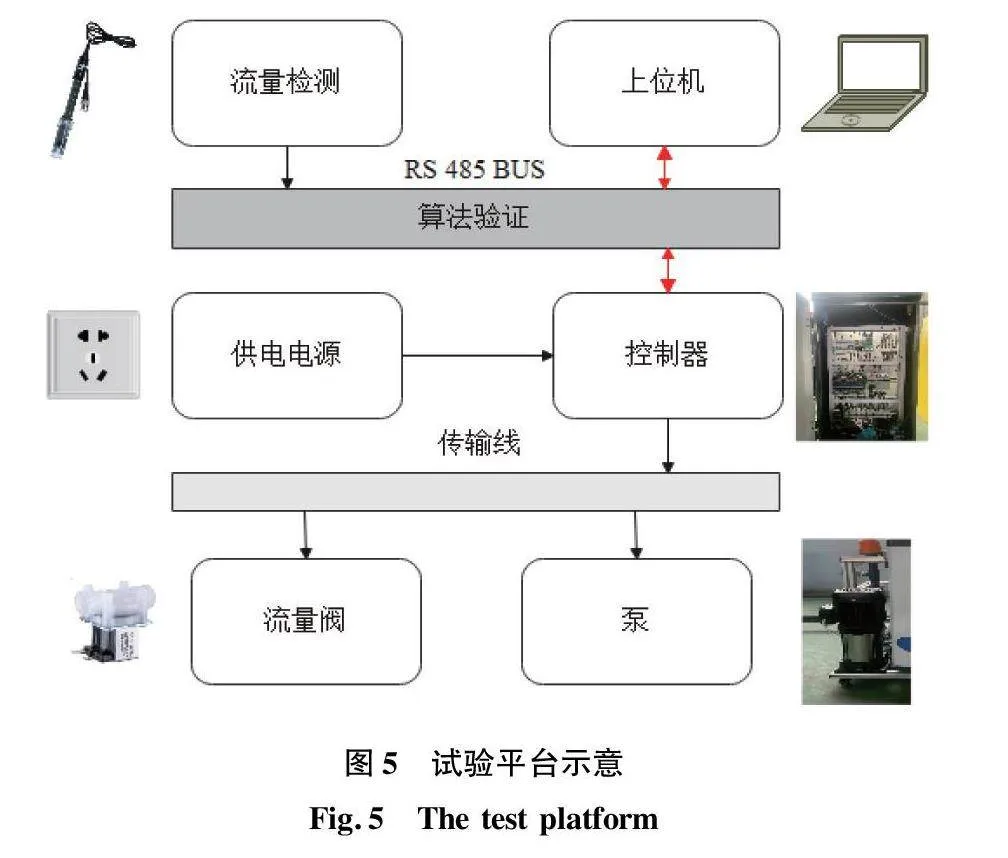
液肥變量控制系統采用基于PSO優化的模糊PID控制作為變量控制系統的控制算法，通過控制終端設定目標量，在室內進行參數測試，分別對系統壓強與流量的關系、系統作業精度進行驗證。試驗平臺示意圖如圖5所示。

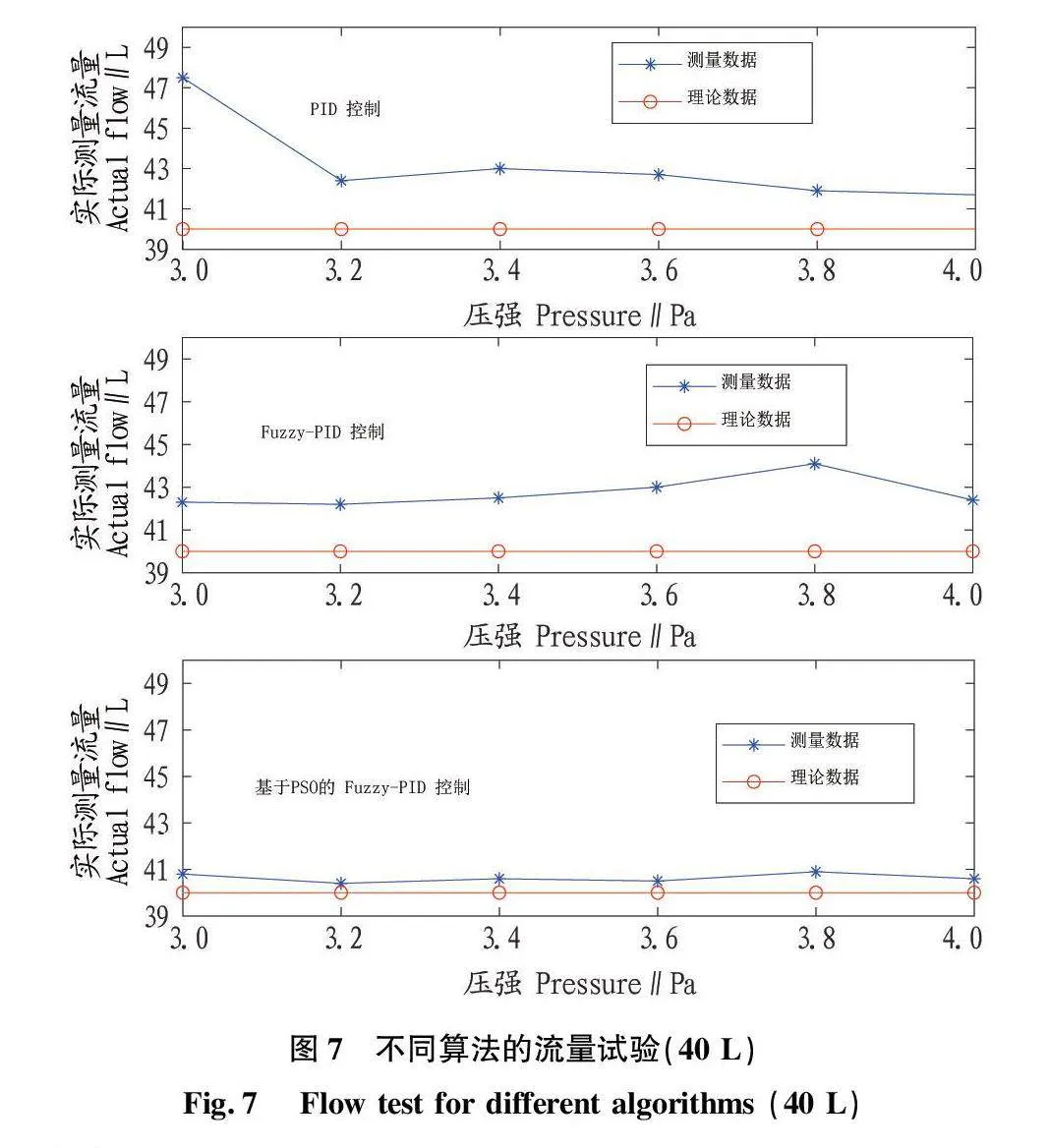
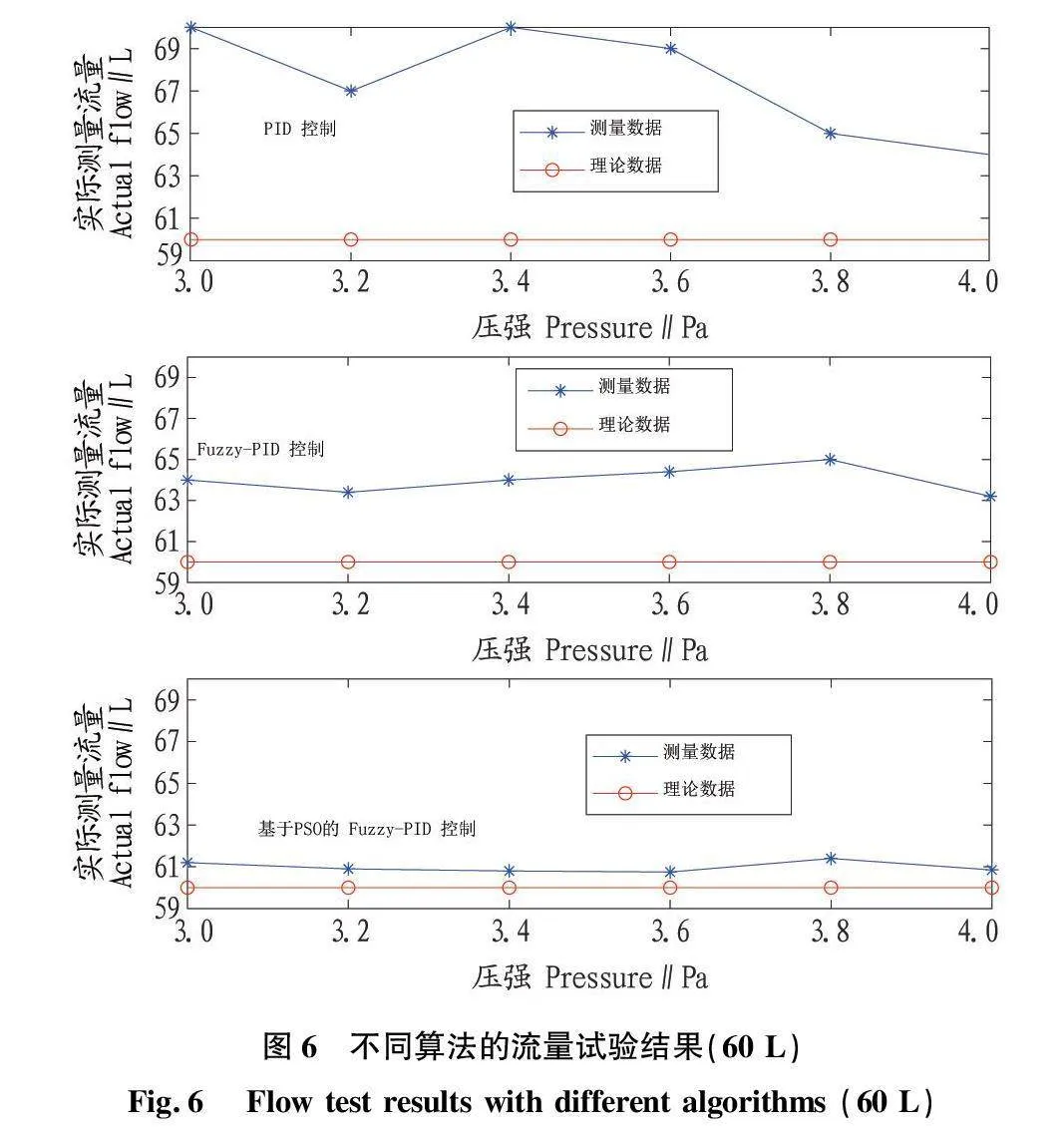
精度是評價變量控制系統的重要指標之一。通過設定目標流量（即理論流量），測得實際作業中實際流量，從而驗證液肥變量控制系統的作業精度。設置相同壓強值，分析不同控制算法下施肥系統的施肥精度，測量5組實際流量數據，取平均值作為實際流量的測量值。

當理論流量為60 L時，3種控制算法的控制精度分別為6.70%～16.70%、5.30%～8.30%、1.25%～1.50%（圖6）；當理論流量為40 L時，3種控制算法的精度的控制范圍分別為10.00%～18.75%、5.50%～10.25%（圖7）；同樣地，各壓強下精度的變化沒有顯示出規律性，但相較于PID控制與模糊PID控制，該研究提出的控制算法對流量精度的調控取得了明顯效果。

5 結論

筆者提出了一個基于粒子群優化的模糊比例積分微分控制器來優化化肥系統的性能。通過與傳統控制方法的對比，驗證了該文所提出控制器的優點。通過仿真試驗，驗證了該文所提供控制器的優越性。通過平臺測試設計了流量試驗，對比了3種控制算法。結果表明，基于粒子群算法的模糊PID算法具有更好的動態性能，與傳統的PID控制、模糊PID控制相比，響應時間分別減少了52和38 s。在不同的流量值下，該系統的施用精度得到了有效優化。在今后的工作中，筆者所研究的施肥系統應考慮其他算法的優化問題，以更好地適應復雜的調節過程。

參考文獻

［1］ 張新偉，楊會民，陳毅飛，等.水肥一體化設備設計及試驗［J］.農機化研究，2021，43（9）：98-104.

［2］江景濤，楊然兵，鮑余峰，等.水肥一體化技術的研究進展與發展趨勢［J］.農機化研究，2021，43（5）：1-9.

［3］ 袁寄望，朱德蘭，高灑灑，等.基于數值模擬的射流式吸肥器結構尺寸優化及性能試驗［J］.農業工程學報，2021，37（14）：52-59.

［4］ 胡昕宇，嚴海軍，陳鑫.考慮肥料溶解的壓差施肥罐出口肥液濃度計算方法［J］.農業工程學報，2020，36（24）：99-106.

［5］ 李頎，馬琳，王康.水肥一體化施肥機EC和pH改進自抗擾解耦控制［J］.中國農機化學報，2020，41（2）：161-170.

［6］ 劉艷妮，同延安，馬臣，等.陜西地區果園土壤pH現狀及調節措施［J］.陜西農業科學，2019，65（10）：58-61.

［7］ 彭娜，王開峰，謝小立，等.長期有機無機肥配施對稻田土壤基本理化性狀的影響［J］.中國土壤與肥料，2009（2）：6-10.

［8］ 全彥濤，李建，張華南，等.化肥減量配施有機肥對信陽茶園土壤養分及春茶品質的影響［J］.河南科學，2020，38（11）：1781-1785.

［9］ 呂昊暾，胡召田，于泳超，等.果園高位作業平臺自動調平前饋PID控制方法［J］.農業工程學報，2021，37（18）：20-28.

［10］ 周明寬，夏俊芳，鄭侃，等.基于變增益單神經元PID的秸稈旋埋還田導航系統研制［J］.農業工程學報，2021，37（5）：31-40.

［11］ 李冬冬，張立新，李春志，等.基于PLC控制的棉田水肥一體化控制系統設計［J］.農機化研究，2021，43（6）：100-104.

［12］ 代擁軍，姜浩，駱東松，等.基于模糊自適應PID控制的智能配肥系統的設計與試驗［J］.計算機與數字工程，2020，48（9）：2131-2135.

［13］ WU C C，CHEN X W，HAN Y X，et al.System modeling and control of automatically variable rate fertilizer applicator［C］//2004 IEEE international conference on systems，man and cybernetics.The Hague：IEEE，2004.

［14］ 牛寅，張侃諭.輪灌條件下灌溉施肥系統混肥過程變論域模糊控制［J］.農業機械學報，2016，47（3）：45-52.