數學折紙實驗的教學價值

摘要:在現實生活中,折紙不僅可以鍛煉手指的靈活性,還可以培養智力.數學折紙實驗是通過對不同形狀的紙片進行一系列的折疊操作,從而形成不同的幾何圖形,進而探索幾何圖形性質的數學實驗.在數學課堂中借助折紙實驗開展教學,不僅有助于學生掌握必備的基礎知識和基本技能,還可以培養學生的抽象思維和推理能力以及創新意識和實踐能力,并促進學生在情感態度與價值觀等方面的發展.
關鍵詞:折紙實驗;數學教學;核心素養
數學是研究數量關系和空間形式的科學,它源于對現實世界的抽象.本文通過設計貼近學生生活且有一定思維價值的折紙活動,變“聽”數學為“做”數學,使學生在課堂上手腦并用,更好地學習數學,培養學生自主探索、動手實踐和合作交流的能力.
1折紙實驗助力學生感悟數學
在自然數的基礎上,因為分配以及精確丈量土地和數學本身的需要產生了分數.在實際教學中,如何在學習了整數的基礎上,讓學生突破已有知識經驗來認識分數是學習的難點.對此,在教學中,教師可以通過折紙實驗讓學生直觀地對分數產生感性認識.例如,對于“拿出正方形紙片折一折,取其中一部分涂上顏色,涂色部分占正方形紙片的幾分之幾”這個問題,在折疊過程中,學生可以依據重合部分面積相等,輕松認識到正方形紙片被分XAbTG9IUVsAko+9xU4h7W9A9HfWQOXiB8ca88VJVOSE=成了面積相等的若干部分,并在進一步涂色的過程中,直觀感受分數的變化、分數的性質、分數的加法運算等.
幾何學習在歷史上經歷了三個階段:無意識的幾何學、科學的幾何學、論證的幾何學.在教學中,學生首先需要通過無意識的形式,或簡單的工藝勞作,或對自然界中的現象進行簡單觀察來熟悉幾何概念.其次在感性認識的基礎上,學生通過實驗歸納出一系列幾何事實.最后學生以推理演繹的形式學習幾何學的論證.
例如,在小學階段的“長方形和正方形的認識”的學習中,怎么認識它們的特征呢?對此,可結合學生的生活經驗,開展“折一折”的折紙實驗.在實驗過程中,學生會發現,把長方形對折一次,兩邊正好重合;對折兩次,四個角也正好重合,所以上下、左右兩組對邊分別相等,四個角相等.通過折紙活動學生認識到長方形對應邊、對應角相等的基本性質.對正方形可進行類比操作,讓學生掌握正方形四條邊都相等,四個角都相等的基本性質.此外,教師可讓學生進一步思考“如何用一張長方形紙片折出一張最大的正方形”,通過實驗將結果直觀地呈現到學生面前,幫助學生理解與掌握.在操作活動中,學生不僅積累了認識平面圖形特征的活動經驗,也為他們今后繼續研究其他平面圖形的特征打下基礎.
進入初中以后,學生的幾何學習逐步進入演繹論證的論證幾何學階段.對此,教師可通過“折三角形三線”的活動,讓學生經歷折三角形的高線、角平分線、中線的形成過程,借助折紙中“對應邊、對應角相等的基本性質”,加深對“三線”的認識,并探索出三條中線、三條角平分線、三條高線都交于一點的共同特征.同時,讓學生通過體會銳角三角形、直角三角形、鈍角三角形三條高線相交情況的不同,認識三角形中的重要線段.
綜上,在教學過程中,折紙實驗可以讓學生親身經歷知識產生的過程,使幾何概念、幾何事實以更加直觀的形態呈現在學生眼前.同時,在感性認識的基礎上,教師啟發學生進一步進行歸納論證,進而學習論證幾何學,發展學生的抽象思維與邏輯推理能力.
2折紙實驗啟發學生邏輯思考
用演繹法證明或者證偽一個數學命題之前,首先需要教師進行猜想,猜想需要通過直覺、觀察、類比、實驗或者其他經驗方法引導學生的思維.折紙實驗正是提供了激發學生猜想的契機,但隨著學生知識與思維水平的提高,折紙實驗的運用不應僅局限在對數學事實的發現上,還需要學生進一步思考事實背后的數學原理.學生在通過實驗方式獲得數學事實“如何”的基礎上,還要用演繹方式去證明“為何”是這樣的.
案例1:折等腰三角形.
活動要求:不限方法,從一張長方形紙片中剪出一個等腰三角形.思考并交流所剪的三角形為等腰三角形的理由.得到等腰三角形后,通過折疊操作,發現等腰三角形的軸對稱性,繼而探索出等腰三角形的性質,即等邊對等角、三線合一.
活動過程:學生通過折紙的方式剪出等腰三角形.通過折紙前后對應邊相等的基本活動經驗,學生發現等腰三角形腰相等的基本事實,并通過折疊等腰三角形,探索得出等腰三角形的基本性質.折紙實驗不僅可以幫助學生發現數學事實,還可以幫助學生尋找證明的方法.在折疊等腰三角形的過程中,借助“折三角形三線”中積累的基本活動經驗,學生從構造中線、高線、角平分線輔助線的方式進行邏輯論證.
案例2:折菱形.
活動過程:
(1)利用矩形紙片折出菱形.
把一張矩形紙片ABCD按照如下步驟進行折疊:
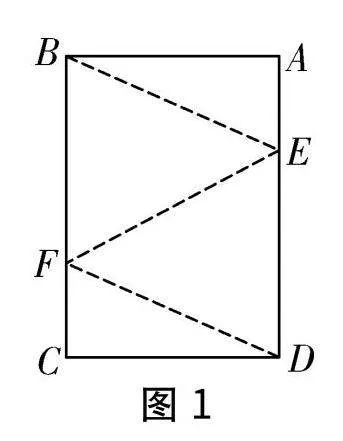
將矩形紙片ABCD沿某條直線折疊,使點B與點D重合,得到折痕與AD,BC的交點E,F(如圖1).請你證明四邊形EBFD是菱形.
(2)利用三角形紙片折出菱形.
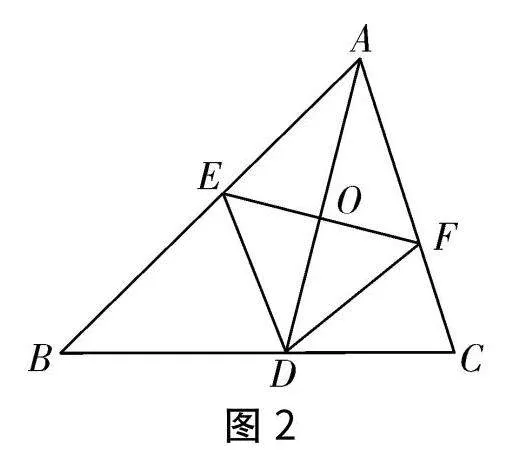
從矩形紙片中剪出一個三角形紙片ABC,按照圖2的步驟進行折疊:
①將三角形紙片ABC沿過點A的某條直線折疊,使AB與AC重合,得到折痕與AC的交點D;
②再將三角形紙片ABC沿某條直線折疊,使點A與點D重合,得到折痕與AB,AC的交點E,F.請你證明四邊形EAFD是菱形.
圖1圖2
(3)你還能設計出其他折出菱形的方法嗎?
在這個實驗過程中,以開放的問題,讓學生根據菱形的性質,探究操作方法.學生通過操作得到菱形,并用多種方法來說明所得到的四邊形為菱形.在此過程中,學生的數學思維得到啟發.學生從實驗中發現規律,獲得理解數學知識的現實材料,從而發展推理能力.
通過折紙活動,學生體驗到了探索、推理數學事實的動態過程.同時,帶著問題進行操作的教學方法,不僅提高了學生思考和理解問題的敏銳性,還幫助學生發展分析問題和解決問題的能力.
3折紙實驗促進學生深度思考
借助折疊實驗,學生在多次操作和不斷探索中,提高了分析問題與解決問題的能力.折紙活動的開放性,也給學生提供了想象的空間,并讓其發揮學習的自主性,進而提升創新意識和實踐能力.
案例3:折等邊三角形.
活動1: 如何用一張正方形紙片ABCD折出一個等邊三角形?
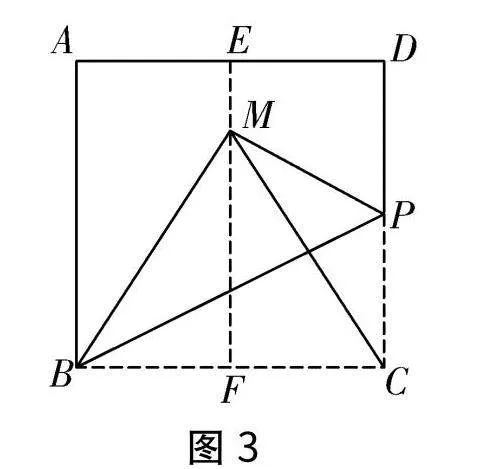
方法1:將紙片ABCD對折得到折痕EF,沿點C翻折紙片,使點C落在EF上的點M處,連接BM,△BCM即為所求的等邊三角形(如圖3).
方法2:將紙片ABCD對折得到折痕EF,沿點A翻折紙片,使點A落在EF上的點M處,連接CM,△BCM即為所求的等邊三角形(如圖4).
兩種方法都基于等邊三角形的判定方法——三邊相等.借助正方形邊長相等的知識,學生首先想到的是利用折疊的方式,使A、D兩點重合.在操作過程中,學生發現A、D的重合點在正方形的對邊中點連線上,從而受到啟發先將紙片對折得到折痕EF.
活動2: 如何用一張矩形紙片ABCD折出一個等邊三角形?
方法1:從矩形中折出一個正方形紙片,然后將問題轉化成活動1的問題.
方法2:類比活動1中的方法.
第1步,對折矩形紙片ABCD(AB>BC),使AB與DC重合,得到折痕EF,把紙片展平.
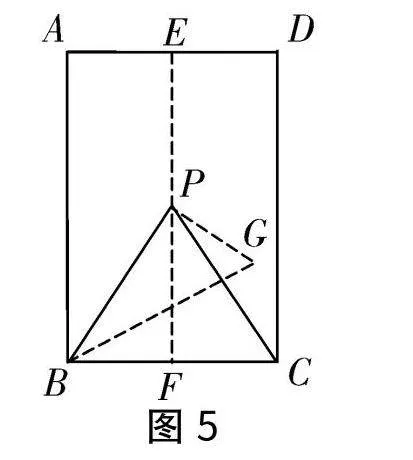
第2步,再一次折疊紙片,使點C落在EF上的P處,并使折痕經過點B,得到折痕BG,連接PB、PC,得到△PBC(如圖5).
方法3:運用活動1得到的結論.
第1步,對折矩形紙片ABCD,使AD與BC重合,得到折痕MN,將紙片展平.
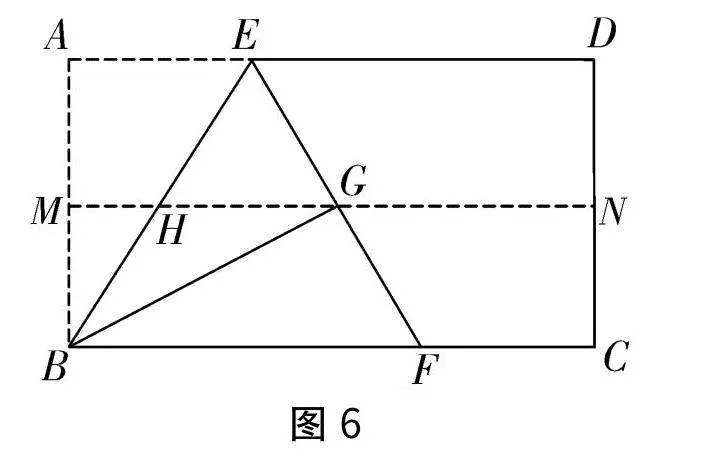
第2步,再一次折疊紙片,使點A落到MN上的點G處,延長EG,交BC于點F,連接BE,交MN于點H,△BEF即為等邊三角形(如圖6).
活動3:如何在正方形紙片中,折出一個最大的等邊三角形?
作為開放性設計的折紙實驗,設置階梯問題可以給學生空間,讓學生充分地思考問題,并借助已有的數學知識與折紙活動經驗,多角度發散思維.在折紙活動中,學生手、眼、腦三位一體協調發展,而層層遞進的問題設置,更是不斷推動著學生實踐能力和創新意識的發展.
4折紙實驗提升學生數學素養
在活動中驗證數學命題,不僅給學生的猜想提供機會,更是增加了數學學習的趣味性.靈活的折紙操作,讓學生看到生活中的數學,用數學的眼光觀察現實世界.折紙后的深度思考,啟發學生用數學的思維思考現實世界,用數學的語言表達現實世界.
案例4:A4紙的秘密.
工作生活中印刷紙大小的變化規律:A0紙長度方向對折一半后變為A1紙;A1紙長度方向對折一半后變為A2紙;A2紙長度方向對折一半后變為A3紙;A3紙長度方向對折一半后變為A4紙……這種關系中蘊含著冪運算.為保證放大或縮小文檔不會出現圖文失真,A系列不同型號紙張的長寬比會保持固定的比值,所以不同型號紙張存在相似性.從相似的角度,
我們可以推理出A系列紙張的長寬比為2,也可以從折紙的角度去驗證它是否滿足長寬比為2.
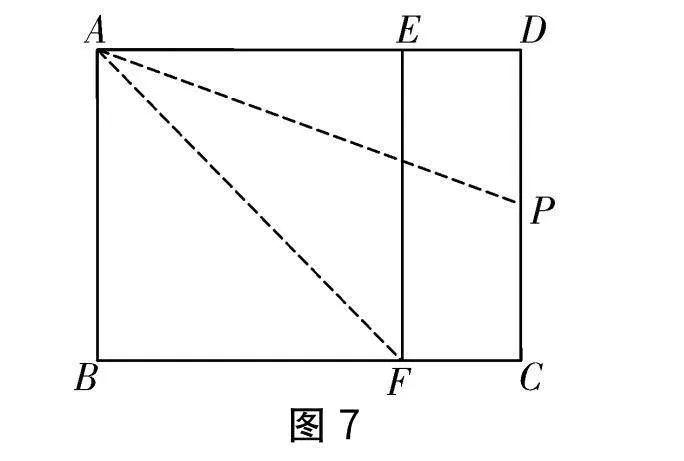
如圖7所示,將矩形紙片ABCD(AD>DC)沿AF對折,使得點B落在AD邊上點E處,得到正方形AEFB.然后將AD沿AP折疊,使AD與AF重合.若點D與點F重合,則矩形ABCD長寬比為2.
折紙實驗的素材來源于日常生活,操作簡單,易于在課堂中實現.筆者曾經以亂扔紙飛機為契機,帶領學生探究紙飛機中折痕長度、折疊角度大小的活動.課堂上同學們都積極獻計獻策,靈活運用知識去解決設計的問題.課后,意猶未盡的學生們相互折紙,讓對方去求解.當學生對事物有了更深入的理解后,思維也會更深刻,活動也將不再局限于事物的表面.這次活動后,班級內也很少出現亂扔紙飛機的現象了.
5結語通過折紙活動,學生能關注到生活中與數學相關的信息,主動用數學的眼光看待生活.在深入思考折紙實驗中的數學問題時,學生能夠克服困難,樹立學好數學的信心,體會數學的價值,欣賞并嘗試創造數學美.同時,在活動過程中,學生也能養成認真勤奮、獨立思考、交流合作、反思質疑的學習習慣.

