基于新課標的高中數(shù)學建模教學實踐研究

摘要：開展數(shù)學建模活動對培養(yǎng)高中生數(shù)學核心素養(yǎng)具有促進作用，能夠使學生將理論與實踐緊密結合，使高中數(shù)學教學實現(xiàn)培育優(yōu)秀人才的目標，與新課標教育理念緊密融合，培養(yǎng)高中生的數(shù)學關鍵能力.本文從新課標出發(fā)，論述數(shù)學建模教學思路的重要性，致力于提高數(shù)學課程教學質量與效率和培養(yǎng)高中生數(shù)學學科綜合素養(yǎng).

關鍵詞：新課標；高中階段；數(shù)學建模；教學實踐

高中數(shù)學教學旨在從理論教學切入，發(fā)展學生實踐能力.教師應以《普通高中數(shù)學課程標準（2017年版2020年修訂）》（以下簡稱“新課標”）為依據(jù)，將數(shù)學建模思想融入教學活動，為高中數(shù)學建模教學提供實踐平臺，發(fā)展學生綜合能力.［1］高中階段是學生抽象思維進階的關鍵期，對于提高學生數(shù)學抽象思維能力具有促進性作用.鑒于此，在高中數(shù)學教學中，教師應優(yōu)化數(shù)學建模教學實踐活動，體現(xiàn)學生本位思想，發(fā)展數(shù)學能力，全面培養(yǎng)學生實踐學習能力.本文從數(shù)學實踐活動視角出發(fā)，以“周期現(xiàn)象的描述”教學為例創(chuàng)設數(shù)學建模教學實踐活動，以期提高學生數(shù)學建模素養(yǎng)和數(shù)學學習能力.

1“周期現(xiàn)象的描述”教學分析

1.1學情分析

（1）知識基礎.“周期現(xiàn)象的描述”主要是對“函數(shù)”知識的教學.教師通過正弦函數(shù)、余弦函數(shù)、正切函數(shù)知識點的教學培養(yǎng)學生的函數(shù)模型思維，使學生能夠在本課時學習中掌握重要知識點，初步建構數(shù)學模型思想.例如，在學習正弦函數(shù)與余弦函數(shù)知識點時，教師幫助學生了解數(shù)學模型在數(shù)學中的重要性，給予學生變式思維的啟迪，深層剖析函數(shù)的關系，增強學生的函數(shù)建模能力，促zhiDt0QW/UYujuGJ4g/xG4BhZGkHKYWyXbKnfJ+ZJ58=進學生數(shù)學建模思想發(fā)展.［1］高中數(shù)學建模學習分為三個階段：第一階段，設在人教B版《普通高中教科書數(shù)學必修第一冊

》中，學生初識數(shù)學建模思想，初步掌握模型思維的形成路徑和方法，掌握報告撰寫的技巧；第二階段，設在人教B版《普通高中教科書數(shù)學必修第二冊》中，在教師的指導下，學生能夠了解建模的應用路徑和適用對象，具備簡單的模型思維；第三階段，設在人教B版《普通高中教科書數(shù)學必修第三冊》中，教師開展數(shù)學建模活動，促使學生用數(shù)學方法解決實際問題.

（2）思維能力.在第三階段學習中，學生能夠在抽象思維的基礎上，利用簡單的數(shù)學模型對知識點進行分類、歸納與總結，強化數(shù)學知識整合應用，形成數(shù)學建模思想，強化數(shù)學抽象思維能力.

（3）情感態(tài)度.高中階段是學生升華探索精神的關鍵時期，在經(jīng)歷數(shù)學建模活動后，學生能夠具備良好的合作學習精神、自主鉆研精神，能夠更加嚴謹、深入地開展學習活動，為形成良好的數(shù)學學科核心素養(yǎng)奠定堅實基礎.

（4）學習障礙.第一階段和第二階段的建模活動相對簡單、直觀，第三階段的建模活動具有抽象、復雜的特點，使得學生在面對這一階段的建模活動時，容易產(chǎn)生畏難情緒，無法運用數(shù)學建模思想解決實際問題.同時，高中生解題過程中，容易將數(shù)學建模思想的運用錯誤理解為解答數(shù)學應用題，導致課程學習效率與質量降低.

1.2教學目標分析

教師對學生進行細致觀察，了解高中生的數(shù)學學情，結合學生已有知識基礎和身心規(guī)律，科學開展教學創(chuàng)新工作，深入滲透數(shù)學建模教學內容.教師應緊密關聯(lián)新課標，設計出具有特色的建模教學活動，制定出詳細的教學計劃.

（1）情境與問題.在“周期現(xiàn)象的描述”的教學中，教師要引導學生自主學習，在具體情境、教學資料中提出問題，在數(shù)學模型建立與檢測中解決實際問題，促使學生數(shù)學思維經(jīng)歷從現(xiàn)實到情境再到現(xiàn)實的過渡，切實提高學生自主學習能力.

（2）知識與技能.在探究“周期現(xiàn)象的描述”這一知識點時，教師幫助學生掌握“周期變化”的規(guī)律、特點，將理論與實際緊密融合，科學探索三角函數(shù)知識，為學生綜合性發(fā)展開辟全新路徑.

（3）思維與表達.教師利用“周期現(xiàn)象的描述”建模實踐活動，引導學生探索y=Asin（ωx+φ）的函數(shù)公式，并利用函數(shù)表達的方法說明海水在一天內深度的變化過程，學生了解數(shù)學模型教學的主要方向和具體目標.

（4）交流與反思.通過完整的數(shù)學模型學習，學生能夠形成獨立意識和系統(tǒng)思維，進而主動與同學、教師等交流學習心得體會，分享自己的收獲.學生自主體悟數(shù)學知識與生活實際的緊密聯(lián)系，逐步建構自主、獨立的數(shù)學建模思想，為形成良好的數(shù)學建模習慣做好鋪墊.

1.3重點和難點

重點：教師引導學生感受數(shù)學建模從現(xiàn)實到情境再到現(xiàn)實的過程；促使學生掌握開題報告、論文書寫等方式方法，提高其規(guī)劃性學習能力.

難點：Excel 和 GeoGebra 的簡單運用.

2教學過程設計

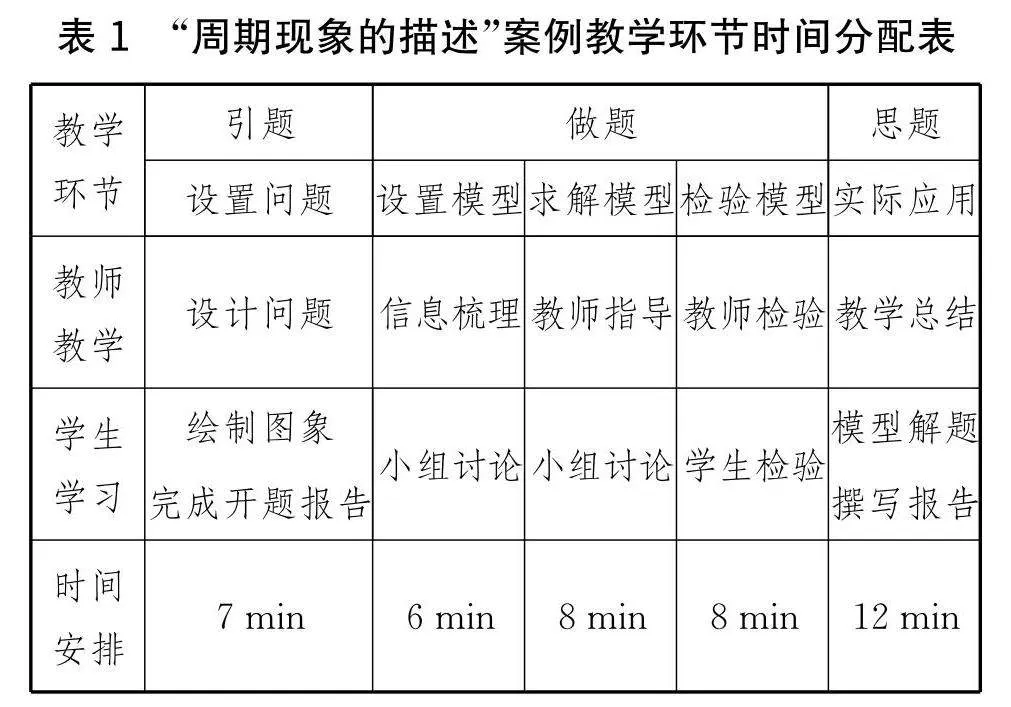
本課時的數(shù)學建模實踐活動主要用“小組合作教學法”幫助學生完成建模準備，提高其對“建模教學”的預習與探索能力.在這一過程中，教師著重培養(yǎng)學生數(shù)據(jù)搜集和數(shù)據(jù)處理能力，提高其綜合能力.基于此，“周期現(xiàn)象的描述”教學設計應略去選題過程，以開題為起點，直接進行實踐教學研究.“周期現(xiàn)象的描述”課堂教學設計中，教師對各個教學環(huán)節(jié)的時間分配進行合理安排，具體安排見表1.

2.1問題情境

海水在24小時內會發(fā)生漲落現(xiàn)象.海上航道的開放與關閉都有規(guī)定的時間.海水上漲時，船只駛進航道；落潮時，船只駛回大海.在這一生活情境中，學生可以用函數(shù)對海水漲落情況進行描述，并探究港口水深與時間的變化.

2.2提出問題

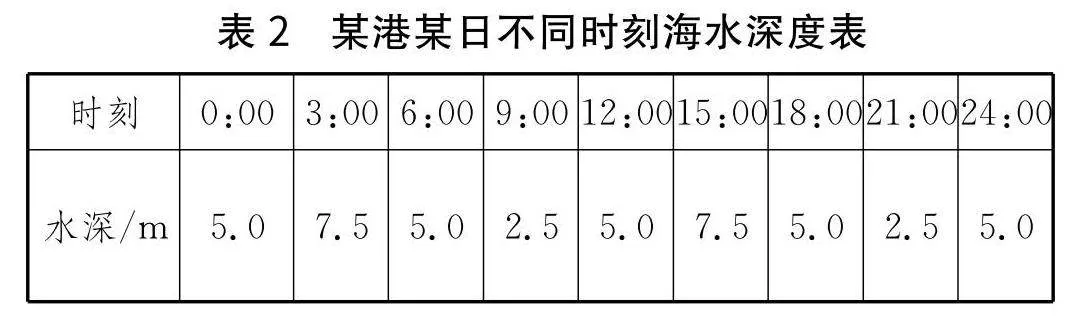
某港某日不同時刻的海水深度如下（見表2）.

師：結合所搜集的數(shù)據(jù)信息，用合適的函數(shù)描述24小時內這一港口的水深與時間的關系.根據(jù)二者的關系，探究各個整點時間的水深近似值.

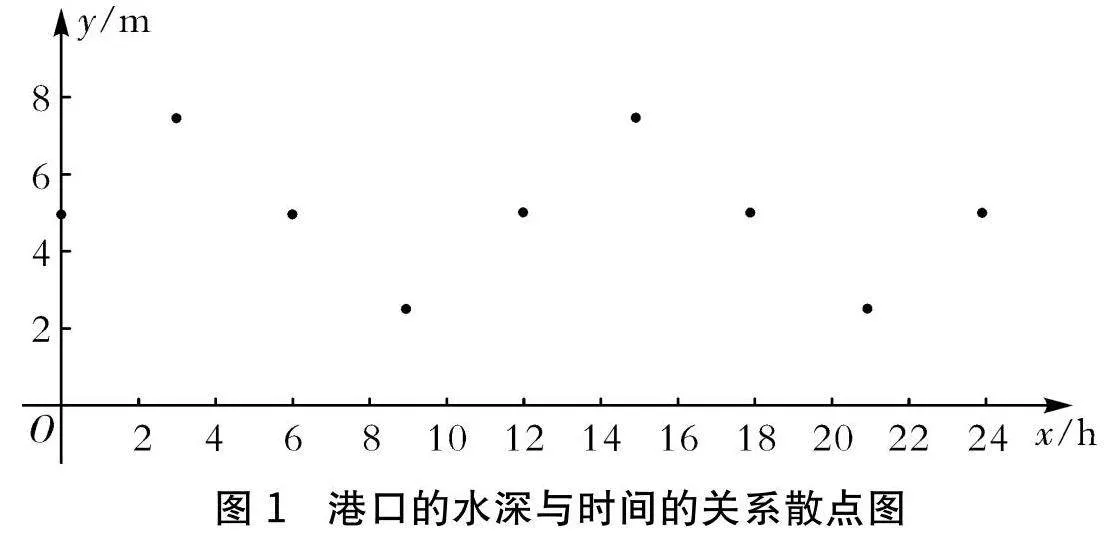
生：在數(shù)據(jù)搜集過程中，能夠獲得準確、真實的數(shù)據(jù)，將這些數(shù)據(jù)進行處理后，可以制作成“散點圖”. 在觀察散點圖后，判斷船只進、離港時間可由哪一種函數(shù)描述.

【設計意圖】新課標著重鍛煉學生質疑能力，促使學生在具體問題中提高函數(shù)認知能力，并以函數(shù)知識為依據(jù)解決數(shù)學問題.這一學習環(huán)節(jié)能夠培養(yǎng)學生數(shù)據(jù)搜集能力和數(shù)據(jù)分析能力，促使學生在分析數(shù)據(jù)過程中了解數(shù)學建模的方法和技巧，由此培養(yǎng)良好的建模思維.同時，在數(shù)據(jù)處理過程中，教師幫助學生強化信息化學習技能，掌握計算機的使用方法.

學習過程：將該港口不同時刻、海水深度的數(shù)據(jù)制作成數(shù)據(jù)關系表.同時，學生將具體數(shù)據(jù)在平面直角坐標系繪制出來（如圖1）.

2.3建立模型

教師組織學生以小組合作的形式圍繞“如何建立模型問題”進行討論.

學生通過小組合作的方式討論數(shù)據(jù)內涵，增強自身函數(shù)學習能力.

【設計意圖】通過本學習環(huán)節(jié)的探索，教師培養(yǎng)學生自主學習、創(chuàng)新學習能力，學生利用散點圖抽象出數(shù)學模型.

活動過程：教師利用散點圖培養(yǎng)學生抽象思維意識.學生根據(jù)散點分布情況確定函數(shù)模型為正弦型函數(shù)，判斷y=Asin（ωx+φ）+h 是否能夠描述水深與時間關系.

2.4求解模型

師：各個小組選擇正弦型函數(shù)，探索模型中的各個參數(shù).

【設計意圖】求解模型過程，學生對模型的參數(shù)進行分析，由此發(fā)現(xiàn)數(shù)學問題的解決方法，形成數(shù)學函數(shù)思想，提高函數(shù)知識解答能力.

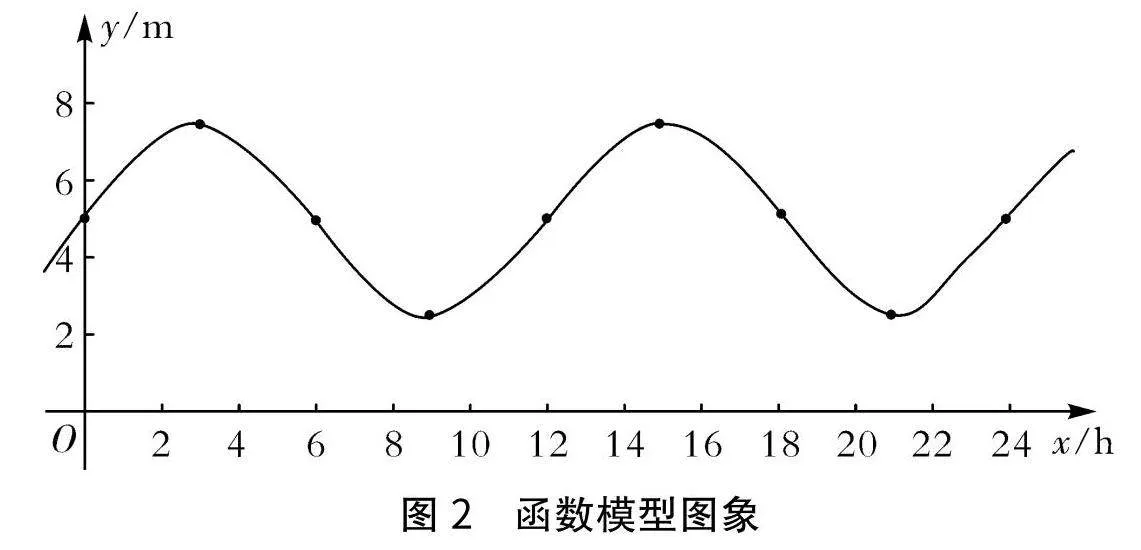
實踐過程：由數(shù)據(jù)、圖象（如圖2）可知，A=2.5，h=5，ω=π6.

將參數(shù)代入模型，得到函數(shù)y=2.5sinπx6+5 ，這一函數(shù)能夠精準地描述某港水深與時間的數(shù)量關系.

2.5檢驗結果

師：同學們思考一下，接下來我們應該如何驗證模型.

生：利用各個學習小組的研究成果，交流數(shù)學模型建構的規(guī)律和方法，由此掌握數(shù)學模型思維，強化學生學習能力.

【設計意圖】在求解過程中，學生利用兩組數(shù)據(jù)進行解題；通過檢測建模模型，強化學生自主學習能力，提高自我檢測技能，深化數(shù)學建模教學效果.

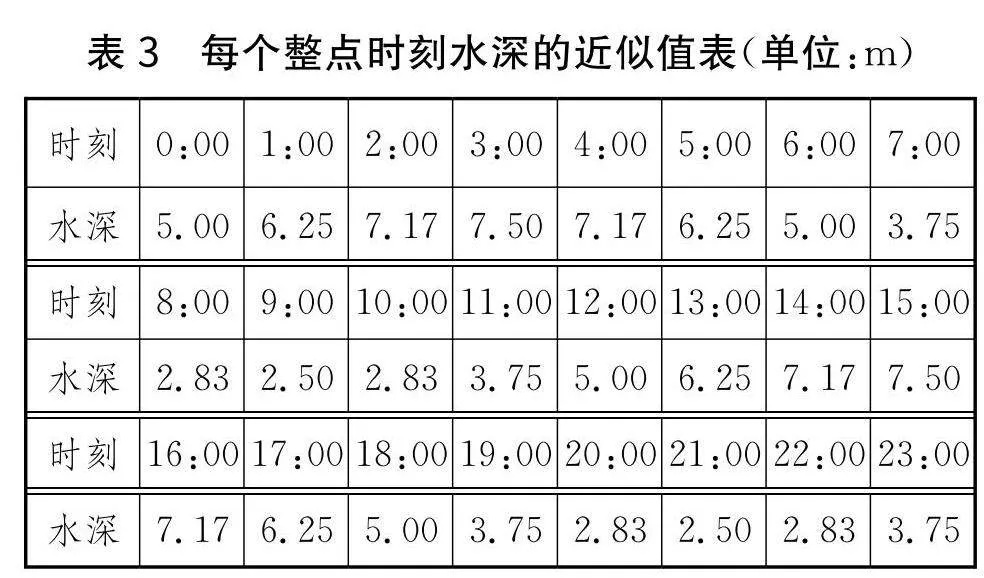
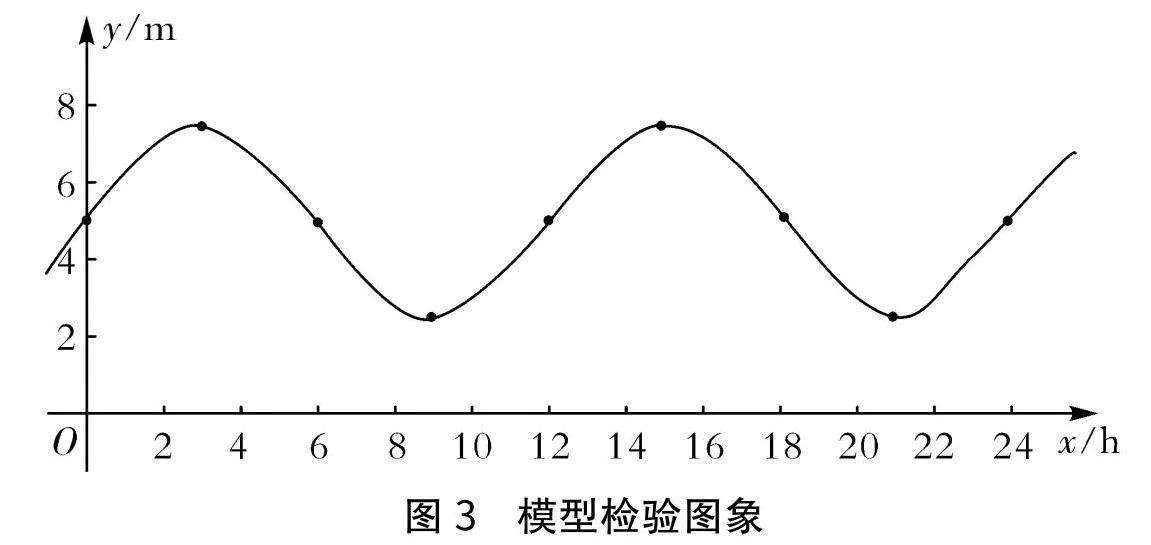
實踐過程：學生將數(shù)據(jù)代入模型之中，通過推理計算檢查是否有誤；將散點與模型融合起來，繪制圖象（如圖3）.

根據(jù)模型推導出整點水深（單位：m）近似值，具體數(shù)據(jù)如下（見表3）.

2.6實際應用

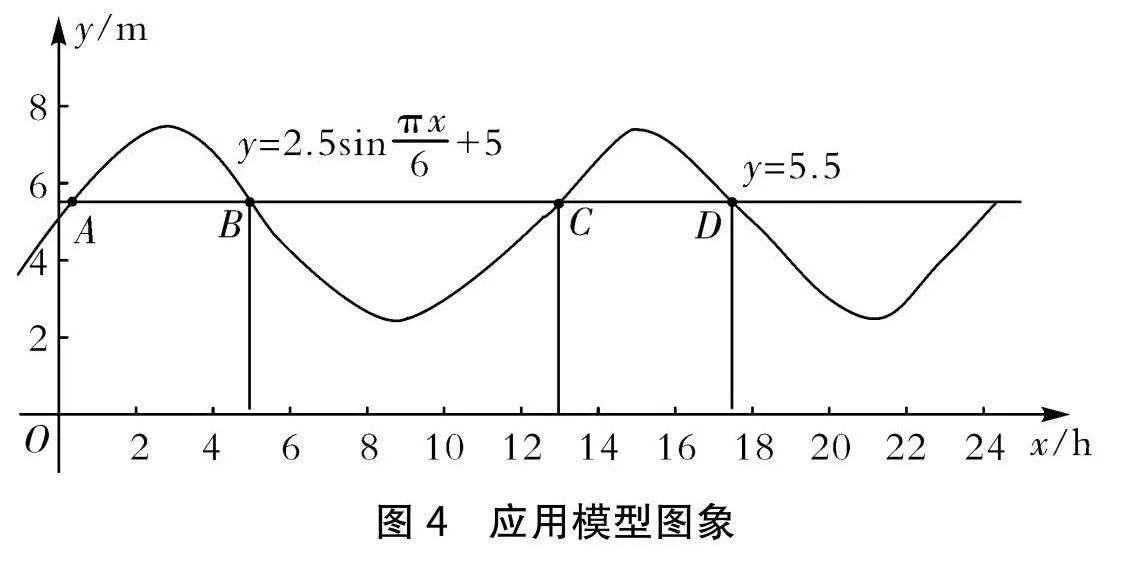
師：船底與水面距離4m，船底與水底最小距離為1.5m，這艘船要想駛進港口，需要在哪一時間，且可停留時間是多少.

生：利用小組合作學習法，在GeoGebra軟件中繪制圖象，分享學習心得體會.

實踐過程：船底與水面距離為4m+1.5m=5.5m，即y=2.5sinπx6+5>5.5.用 GeoGebra 軟件繪制函數(shù)y=2.5sinπx6+5的圖象，并畫出直線y=5.5，得到四個交點 A，B，C，D（如圖4）.

3結語

本文以新課標為依據(jù)，對數(shù)學建模教學實踐活動進行優(yōu)化設計，結合高中數(shù)學建模思想培育目標，制定出符合高中生身心發(fā)展規(guī)律的數(shù)學模型教學方案，致力于培養(yǎng)學生良好的數(shù)學精神，強化學生數(shù)學綜合能力.教師從“周期現(xiàn)象的描述”課程切入，幫助學生將生活實際問題抽象為數(shù)學模型，實現(xiàn)從現(xiàn)實到情境再到現(xiàn)實的學習目標，促進學生數(shù)學綜合能力的發(fā)展.

參考文獻

［1］中華人民共和國教育部.普通高中數(shù)學課程標準（2017年版2020年修訂）［M］.北京：人民教育出版社，2020.