經歷基本活動體驗　參悟宏觀解題智慧

摘要：以試題講評課為例，給出教學設計的基本結構，通過經歷基本活動體驗，參悟宏觀解題智慧，從解題的“術”中感悟數學學習的“道”，培養學生面對問題時的良好心態.

關鍵詞：數學;基本活動經驗;宏觀解題智慧;重“術”;悟“道”

考試，是教學評價的主體形式，它是教學過程的一個重要組成部分.考試評價的目的是全面了解學生的學習過程和現狀，及時調整教學內容和教學節奏，更好地改進以后的教學，從而促進學生的發展.但怎樣講、講什么才能取得良好的教學效果，常常眾說紛紜.縱觀目前的試題講評課，依然大量存在缺乏二次加工處理，就題講題、不加選擇的現象，使很多良好的教學資源白白浪費.

我們知道，試題講評具有診斷、糾錯、示范、引領、鼓勵、提升的作用.每次檢測都是學習過程中的加油站，能起到提示和喚醒的作用.《義務教育數學課程標準（2022年版）》指出：“評價結果要關注學生已有的學業水平與提升空間，為后續的教學提供參考.教師要分析、反思教學過程中影響學生能力發展和素質提高的原因，尋求改善教學的對策.”［1］

試題講評要重視解題方法的分析，即“重術”，這是體驗，是學生認識問題、獲得方法的直接經歷；同時，更要引導學生跳出繁雜的題海，而看到習題之間的聯系和規律性，即“悟道”.這樣才能更好地發揮試題的指向性功能，幫助教師在課堂中落實解題教學的內涵，提升學生的數學核心素養.

最近，筆者在全市范圍內執教了一節市級公開課“杜集區九年級數學質量評價試題講評”.以下是筆者的課堂流程和教學思考，現與讀者分享解題教學中的“術”與“道”.

1 教學過程

1.1 統計歸納，以學定教

設計意圖：試題統計歸納是為了更好地關注學生已有的學業水平與提升空間，了解存在的問題，以使課堂教學有的放矢，為內容的選擇提供有效的參考.

如何能讓學生在面對難題時不產生畏懼情緒，我們要從學生的考試心理入手，為他們創造一個熟悉的情境，喚醒他們潛在的知識儲備，從而有效地解決問題.這就需要教師對試題進行進一步的改造與加工，直逼知識內核，營造解題的最近發展區.

常言道：選擇比努力更重要.因此，把本節課的教學重點就定為掌握計算線段長的一般方法，形成解題策略.

1.2 兩重境界，依術啟智

1.2.1 勾股定理的雙重境界

（1）直接應用：利用勾股定理列方程求各邊長.

例1已知直角三角形的斜邊是6，兩條直角邊的比是1∶2，求兩條直角邊的長.

設計說明：從學生熟知的直角三角形入手，引導學生關注圖形的形成過程，發現幾何模型，體會方程結構在幾何計算中的重要作用.“低起點”就是在接近學生認知最近發展區的地方開始探索之旅，增強他們解題的自信心.

（2）創造性應用：題中沒有直角三角形，需要我們添加輔助線后構造直角三角形，然后再利用勾股定理.

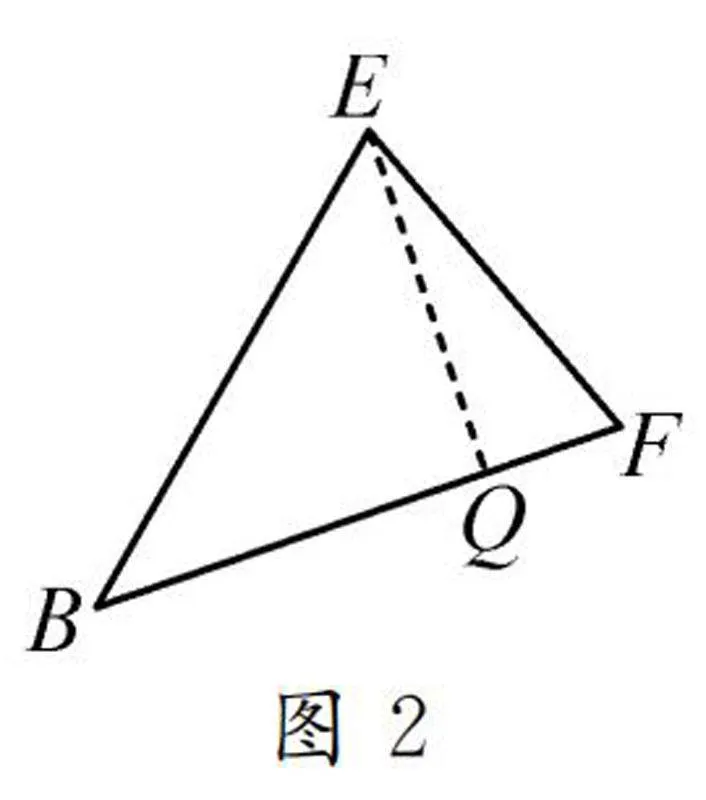
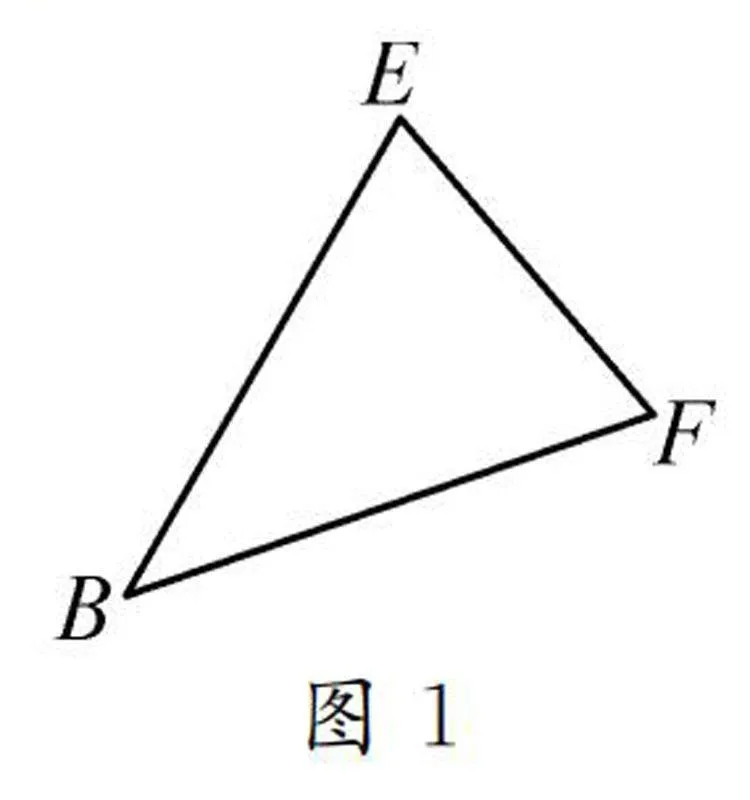
例2如圖1，在△BEF中，BE=BF=5，EF=2，求tan∠EBF.

分析1：如圖2所示，過點E作EQ⊥BF，垂足為Q.在Rt△EBQ和Rt△EFQ中，設BQ=x，分別利用勾股定理把EQ2表示出來，從而列出方程，求出x，進而可以求出EQ，即可求出tan∠EBF.

分析2：在求出BQ之后，也可以先求cos∠EBF，再求出tan∠EBF.

設計說明：為了喚醒學生原有的認知模型，筆者結合試題在例1的基礎上設計了例2，它沒有現成的直角三角形，需要利用化歸思想通過添加輔助線，從而轉化為直角三角形的模型.它們都是從學生反饋的試題中的問題提煉出來的數學模型.幾何模型的建立以及方程結構的喚醒，將有利于把幾何問題轉化為代數問題來解決.“小步子”就是在學生學有所獲的基礎上，及時前行，形成解題的節奏感，感受解題帶來的心靈愉悅.

1.2.2 相似三角形的雙重境界

（1）直接應用：利用相似三角形的性質，得到比例線段，然后列方程求線段長.

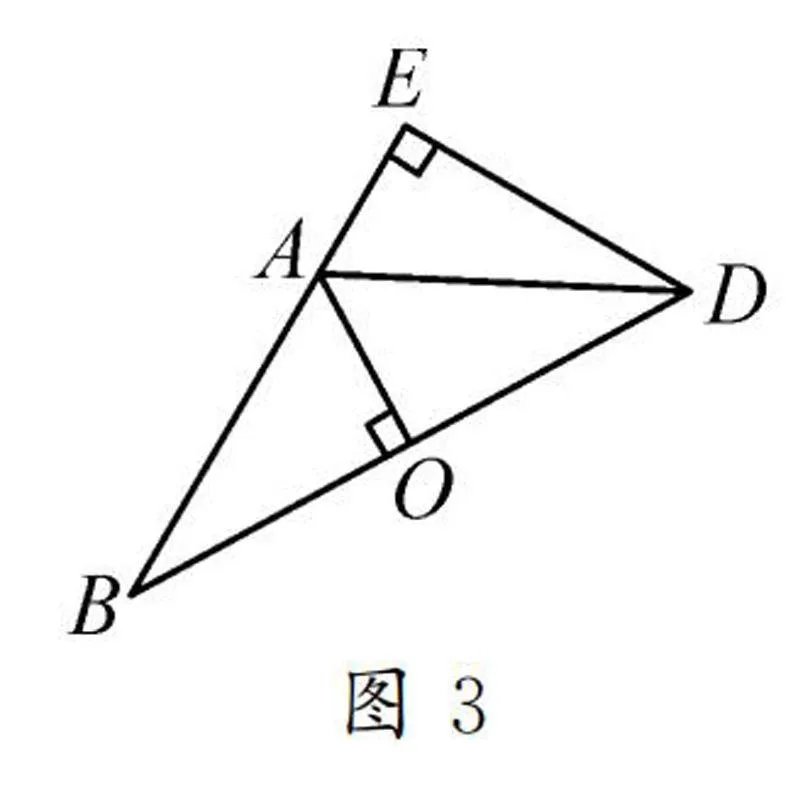
例3如圖3，在△BDE中，∠BED=90°，點A是線段BE上的一點，AO⊥BD，垂足是O，AB=AD=5，OA=3，求DE的長.

分析1：由△BAO∽△BDE可以求出DE.

分析2：在Rt△AOB中，可以求出sin B，同理，在Rt△DEB中，可以得到sin B的另一種表達形式，它們顯然是相等的，從而求出DE.

分析3：根據條件，可以利用BD，AO的長求出△ABD的面積，也可以利用AB，DE的長表示出△ABD的面積，顯然這兩種計算的結果是相同的.

分析4：設AE=x，在Rt△ADE中，可以利用勾股定理把DE2表示出來；同理，在Rt△BDE中，可以利用勾股定理把DE2表示出來.顯然這兩種表示的結果是相同的.求出AE后，就可以利用勾股定理求出DE.

設計說明：本題意在現有圖形的基礎上，引導學生通過自主學習、合作交流，發現相似三角形模型，體會比例線段這種結構在幾何計算中的重要作用.同時，引導學生借助于直角三角形的特殊性質，發現線段計算中利用勾股定理和三角函數所反映出的邊角關系，來完成線段計算的任務.

（2）創造性應用：題中沒有我們需要的相似三角形，這時就要先添加輔助線再構造相似三角形，然后利用比例線段列方程求解.

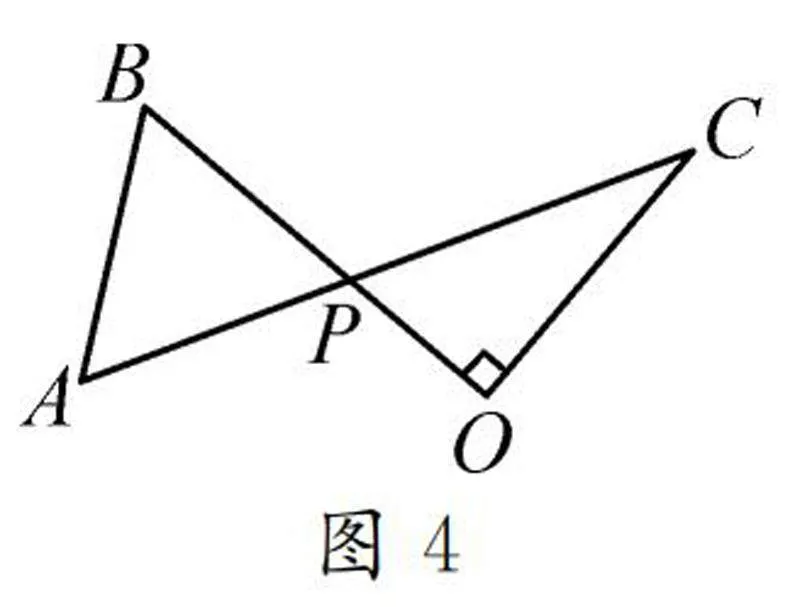
例4如圖4，已知線段AC與OB相交于點P，AB=BP=6，OP=4，OC=8.∠COP=90°，求AP的長.

分析：顯然，圖中沒有相似三角形，無法建立起線段之間的數量關系，這時我們就需要添加輔助線來構造相似三角形.

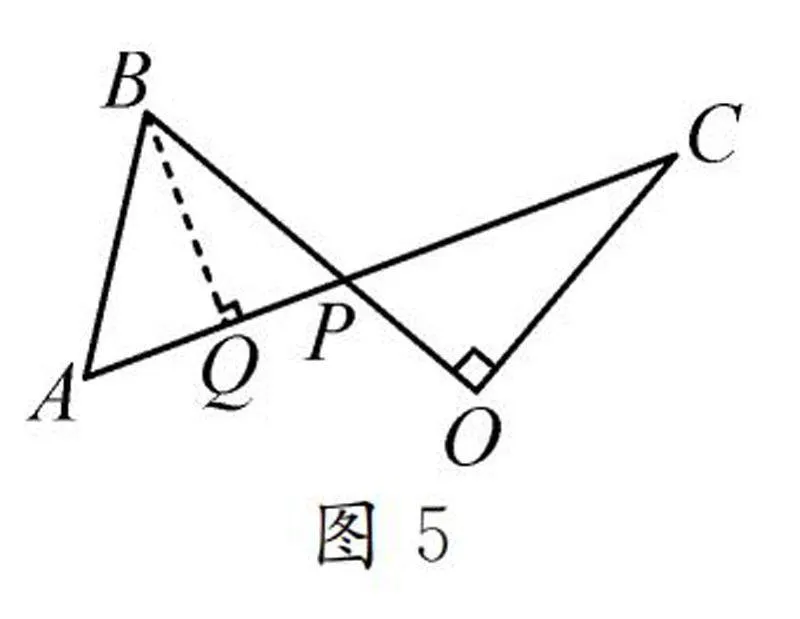
方法1：如圖5，過點B作BQ⊥AP，垂足為Q，則Q是AP的中點，△BPQ∽△CPO，從而求出PQ（也可以用三角函數代換）.

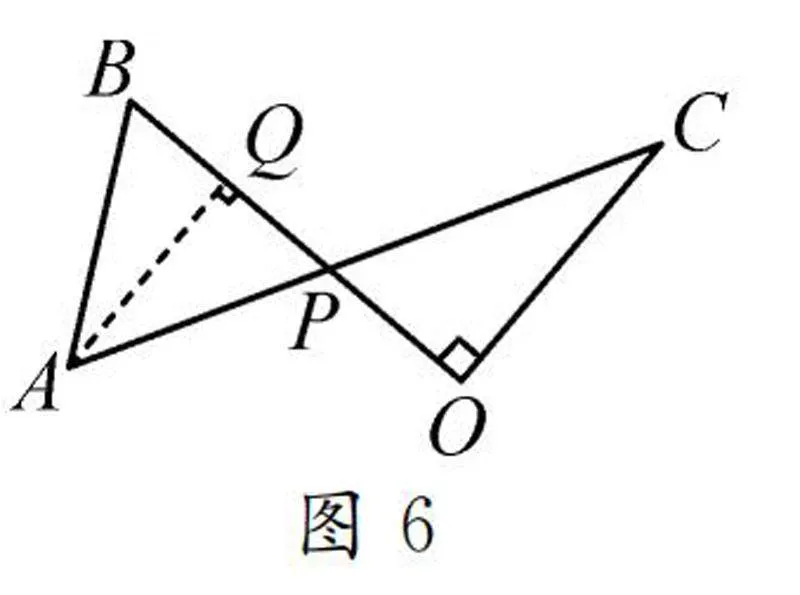
方法2：如圖6所示，過點A作AQ⊥BP，垂足為Q.

易知△APQ∽△CPO，所以PQ／AQ=OP／OC=4／8=1／2.

設PQ=x，則AQ=2x，BQ=6-x，AP=5x.

在Rt△ABQ中，利用勾股定理就可列出方程求出x.

（也可以用三角函數代換.）

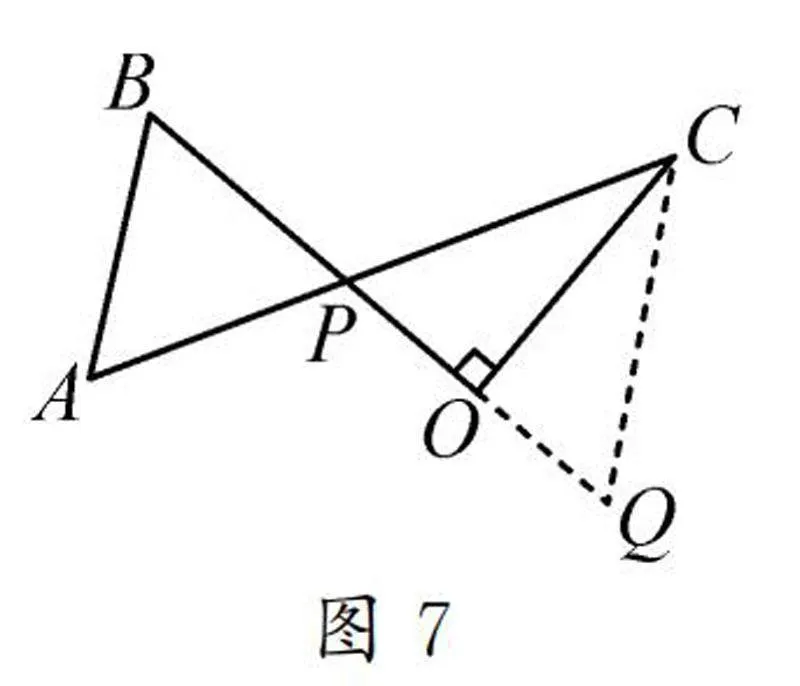
方法3：如圖7，延長PO至點Q，使OQ=OP，連接CQ，則

△APB∽△CPQ，

從而得到AP／CP=BP／PQ.

而CP的長先由勾股定理求得，即可求AP的長.

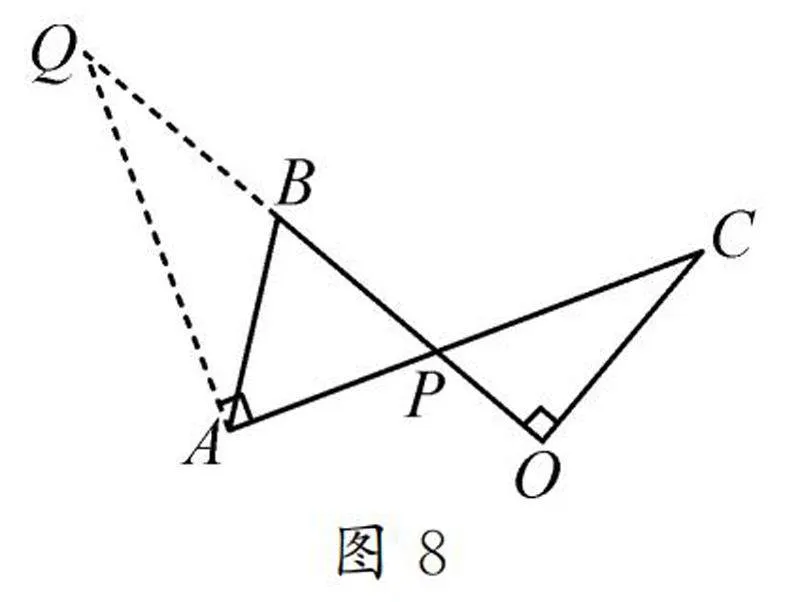
方法4：如圖8，過點A作AQ⊥AC，交OB的延長線于點Q.

易證BQ=BA.

由△PAQ∽△POC，可以求出AP.

（也可以用三角函數代換.）

設計說明：這里的例3、例4也都是從試題中提煉出數學模型.借助于這些模型，不僅為破解難題做準備，同時通過這些模型所隱含的解題方法，熟悉解決這類問題的一般策略，即歸納出解題中的“術”.上課時，教師不要“一言堂”式地“單向輸出”，要通過師生互動、生生互動，由學生自主發現這些方法.

1.3 學以致用，真題顯現

通過知識回顧，熟悉求線段長常見的基本模型及其基本方法，這時再讓學生重新審視試題中出現的原題，以獲得成功的體驗.

設計說明：在數學學習的道路上，學生的興趣來自于學習帶來的成功感.上海市閘北八中劉京海校長曾提出“成功是成功之母”的“成功教育”理念.如果學生在學習過程中，品嘗到的盡是失敗的苦澀，那么他還有什么動力堅持不懈？本課所選的四道例題都不是試題中的原題，但卻是解決試題的“必經之路”，是教師依據試題中出現的模型以及思維方法精心設計的“原創習題”.在學習這四道題之后，破解試題中難題的絆腳石都已攻克，這時再看曾經的攔路虎，就會產生一種柳暗花明、一覽眾山小的感覺，提升解題的自信心，品嘗解題成功的喜悅.

縱觀上述四個例題的各種解法，都是利用勾股定理和相似三角形的性質，通過添加輔助線構造解題需要的圖形，然后在不斷求線段長度的道路上，求出我們所需要的線段長度.

因此，計算線段長的常用解決方法可分為以下兩種類型：

第一類：以構造相似三角形為載體，利用比例線段求解.

第二類：以構造直角三角形為載體，利用勾股定理或三角函數求解.

1.4 盤點收獲，自我成長

（1）通過本課學習，你學會整理試卷的一般方法了嗎？

①按知識點（如勾股定理、相似三角形、二次函數等）分類，整理出與重要概念相關的一般方法.

②按問題（如計算線段長、證明線段相等、求最值等）分類，整理出解決這類問題的一般方法.

③按題型（如選擇題、填空題、作圖題等）分類，整理出解決各種題型的一般方法.

（2）通過學習，你能總結出求線段長的一般路徑嗎？

1.5 學以致用，反思提高

（1）以做過的一套模擬試卷為例，把錯題按知識點進行分類整理.

（2）結合今天所學，總結出計算線段長的一般規律.

設計說明：試題講評課的作業不能僅僅滿足于訂正試題，更要引導學生總結經驗教訓，歸納提升學習收獲，注重知識的整體性和系統性，注重學生學習能力的培養，提高學生的反思意識，這樣才能使學生既見樹木，又見森林.

2 教學反思

著名數學教育家波利亞說：“掌握數學就意味著善于解題.”羅增儒教授說：“數學學習中發生數學的地方都毫無例外地充滿著數學解題活動.”數學學習的最終歸宿就是利用數學知識去解決問題.由于問題的多樣性和不確定性，使我們很容易跌入題海的泥潭難以自拔.如何才能讓學生跳出題海，以“出世”的心態“入世”呢？

高效的試題講評有利于更好地實現“教學評一體化”，以評定教，以評促學，真正做到目標明確，有的放矢.這就是說數學學習不能只滿足于問題解決的“術”，更要從問題解決中提煉出高于具體方法的“道”.

2.1 “有”中生成

前一個“有”是指“看得見”，即解決問題時要發現題目中顯性的文字信息和圖形信息，包括條件和結論.而“生成”是指“生長、拓展”，即把顯性信息通過推理轉換得到進一步有價值的隱性信息，要用運動、發展、變化的觀點看問題，不能“只見樹木，不見森林”，要充分挖掘，做到舉一反三.

2.2 “無”中生有

這里的“無”是指“看不見”，即題中沒有直接給出有價值的文字信息和圖形信息，但這時的“看不見”并不是簡單的沒有和不存在，而是需要我們辯證地看待“無”，提煉出隱藏在背后的有價值的文字或圖形信息.這里的“有”是指“做得出”，即在隱性信息的基礎上，通過聯系、加工、提煉和創造，發現已知和未知之間的潛在關系，構造適當的數學模型，找出解決問題的方案.當然，還需步步謹慎，最后達到“算的對”的結果.

由此可得，解決數學問題的一般流程（如圖9）：

看得（不）見想得到做得出算得對

在“看得（不）見”“想得到”“做得出”“算的對”這四個思維層次中，“看得（不）見”是認知起點，“想得到”是思維關鍵，“做得出”是統籌能力，“算的對”是最終歸宿.

2.3 數學之道

數學學習的終極目標不是學生的分數，而是學生身心的發展.中共中央辦公廳、國務院辦公廳印發的《關于進一步減輕義務教育階段學生作業負擔和校外培訓負擔的意見》明確指出，落實“雙減”學校責無旁貸.古人說：上人用道，中人用術，下人用力.在茫茫題海中，要切實減輕學生的負擔，教師必須為學生點燃學習征途中的指路明燈.顯然，“有”“無”的解題觀是一種在具體解題之上的“高觀點”，是一種哲學視野下的解題觀，它不僅適合某一類題，更適合解決所有的數學問題.它是在學生踏遍千山萬水之后，內心抽象形成的一種素養、一種境界、一種自信，這種心態是自然的、平和的、通透的.

大道至簡，明數學之道，就是要“教會學生思考”，“關注學生的感受”，引導學生通過體驗數學的思維過程，從具體方法中概括出一般原理［2］.在學生經歷的一次次頭腦風暴后，讓深度學習真正發生，使試題講評課給學生帶來身心的“豁然開朗”，從“術”的認知上升為“道”的格局.

參考文獻：

[1]中華人民共和國教育部.義務教育數學課程標準（2022年版）[S].北京：北京師范大學出版社，2022.

[2]章建躍.章建躍數學教育隨想錄：下卷[M].杭州：浙江教育出版社，2017.