基于生本理念的初中數學概念教學探索

自“生本理念”推行以來，筆者反復開展了實踐研究，對數學概念課的教學模式進行了反復試驗與矯正，取得了一定的進展.下面以“隨機事件與概率”的教學為例給出基于“生本理念”的概念教學實踐.

1 教學環節1：復習舊知，感知新知

問題1一次國際乒乓球單打比賽中，甲、乙兩名選手進入最終決賽，值得欣喜的是這兩名選手都是中國選手.現在有幾個問題想考考大家，第一個問題是，這項比賽中冠軍會是中國選手嗎？

生（積極回答）：是.

師（繼續提問）：冠軍會是外國選手嗎？

生（積極回答）：不會.

師（繼續提問）：冠軍是選手甲嗎？

學生（思考后回答）：不確定，有可能是選手甲，也有可能是選手乙.

說明：舊知是新知的基礎，新知又是舊知的引申.在課堂導入環節，筆者引導學生在回顧舊知的同時自然而然地進入到新知的探索中去.教師總結這三個問題的回答過程，強調邏輯推理和分析能力在數學學習和實際問題解決中的重要性.

2 教學環節2：自主探究，獲取概念

問題2想一想，填一填：

（1）問題1中“冠軍是中國選手”，屬于什么事件？

（2）問題1中“冠軍是外國選手”，屬于什么事件？

（3）問題1中“冠軍是中國選手甲”，屬于什么事件？

師（學生分組討論后）：第一組同學，請分享你們對第（1）問的推理過程.

生1：因為甲和乙都是中國選手，所以無論誰贏，冠軍一定是中國選手.我們認為這屬于必然事件.

師：很好，你們確實理解了這個邏輯.那么誰能告訴我為什么這是必然事件？

生2：因為所有可能的冠軍（甲或乙）都是中國人，所以冠軍必然是中國的.

師：完全正確.這就是必然事件的定義——在一定條件下一定會發生的事件.接下來，第二組同學，你們對等（2）問的推理是怎樣的？

生3：因為決賽選手都是中國選手，所以冠軍不可能是外國選手.我們認為這屬于不可能事件.

師：很好.你們準確地識別出了這是一個不可能事件.誰能解釋一下為什么？

生4：因為沒有外國選手參與比賽，所以冠軍不可能是外國選手.

師：完全正確.不可能事件是指在一定條件下一定不會發生的事件.現在，第三組同學，你們是如何推理第（3）問的？

生5：比賽結果不確定，冠軍可能是甲，也可能是乙.我們認為這是隨機事件.

師：很棒.你們正確地識別出了這是一個隨機事件.誰能解釋一下隨機事件的特點？

生6：隨機事件是指在一定條件下，可能發生也可能不發生的事件.它的結果是不確定的.

師：非常好！隨機事件的特點就是它的結果是不確定的.通過今天的討論，我們加深了對必然事件、不可能事件和隨機事件的理解.請大家根據剛才討論的內容，試著填寫表1.

學生根據所學內容完成表1后，教師進行總結并展示答案.

問題3先獨立思考并嘗試列舉必然事件、不可能事件和隨機事件的例子，然后小組合作討論，最終以小組為單位各派一名代表進行全班交流.

說明：筆者抓住學生對“可能性”的認識逐步延展開去，理解概念、歸納概念、分類和識別事件、舉例強化，一步步地讓模糊的概念變得清晰起來，最終在識別和例舉中強化認識，形成清晰的概念框架.

3 教學環節3：適切追問，無痕建構

問題4一個不透明紙箱內放有4個除顏色外完全相同的小球，其中3個紅色，1個白色.那么，從紙箱內任意摸出1個球，它可能是什么顏色？任意摸出1個球時，紅球與白球的可能性是否相同？若不相同，你覺得哪種事件發生的可能性更大？為什么？

師：任意摸出1個球，可能是什么顏色呢？

生：紅色或白色.

師：那摸出紅球的可能性與摸出白球的可能性一樣嗎？

生：應該不一樣吧，紅球3個，白球1個，紅球比白球多，摸到紅球的可能性大.

師：有道理.該怎么證明呢？

生：可以做實驗.

師：很好，請大家分組做實驗并記錄摸出紅球和白球的次數.

學生開始分組做實驗.

師：大家觀察下自己的實驗結果，是不是摸出紅球的次數比白球多呢？

生：是的.

師：該怎么用數值表示這個可能性呢？

學生思考并討論，但沒有新結果.

師：如果是紅、黃、藍、綠4個不同顏色的小球，那么摸到紅色小球的可能性用數值怎么表示呢？

生：1/4.

師：非常好！摸到紅球的可能性是1/4.

說明：在學生思維的最近發展區追問“可能性的大小及如何用數值表示”，讓學生通過深度思考與探究切實理解每個球被摸到的可能性，從而無痕引出概率的概念，為后續的深度探究打基礎.

問題5想一想，說一說：

（1）我們發現，問題4的探究中得到紅球的可能性可以用數值來表示，這就是概率，請試著描述概率的定義；

（2）還是從問題4中不透明紙箱中任意摸出1個球，摸到白球的概率是多少？

（3）還有一個不透明紙箱，其中裝有4個完全一樣的白球，那摸到白球的概率是多少？摸到紅球的概率呢？

（4）基于以上研究，你認為三類事件發生的概率取值范圍是多少？

教師依次引導學生回答第（1）（2）（3）（4）問，從概率的定義到概率的計算逐步深入，進一步明晰本節課所學內容和深化理解本節課知識.具體過程略.

說明：先讓學生用數值去描述可能性的大小，再拋出問題不斷設問，其目的就是讓學生循著之前的探究路徑感知和體驗知識間的聯系，從而深化對概念本質的理解和認識.

4 環節4：變式探究，有效提升

問題6有一枚質地均勻的骰子，小紅隨意將其擲出，求以下各種事件的概率：

（1）向上一面的點數是2；

（2）向上一面的點數是奇數；

（3）向上一面的點數比2大且比5小.

變式以小組為單位試著為問題6設計一個概率問題.

學生分組討論并根據實際情境設計概率問題.

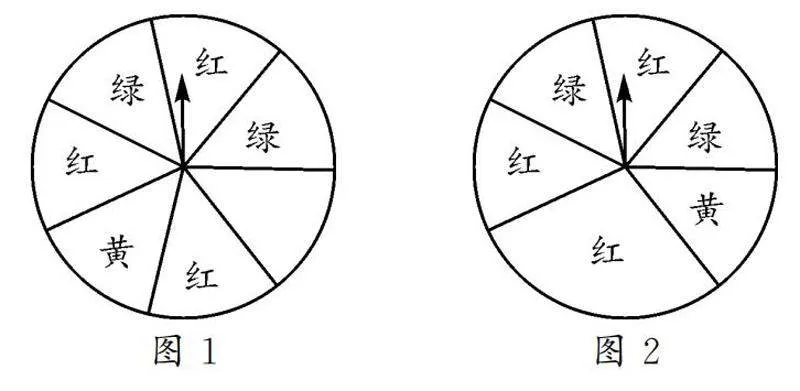
問題7圖1是一個分為7個相同扇形、可自由轉動且指針固定的轉盤，共有紅、黃、綠三種顏色，轉動轉盤后待它自由停止，指針會指向某個扇形所在區域（當指針指向交線則默認指向右邊扇形）.

（1）指向紅色的概率是多少？

（2）指向紅色或黃色的概率是多少？

（3）不指向紅色的概率又是多少？

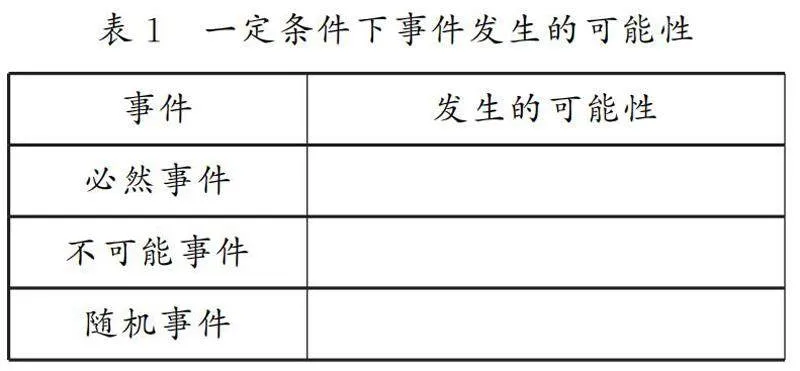
變式將問題7中的轉盤換成圖2所示的轉盤，其他條件和問題均不改變，請回答上述問題.

學生根據所學知識思考后回答問題.

說明：筆者通過改編教材例題并設計變式，深化學生的理解與認識，同時促進學生對概念的深刻理解.

5 環節5：整合梳理，深化認識

教師帶領學生梳理單元知識并在黑板上書寫本課知識結構圖（圖略）.

說明：在梳理知識結構圖的過程中，每個學生都能積極參與，使得不同的學生得到不同的發展，真正落實了“以生為本”的教學理念.

總之，“生本理念”為我們的課堂教學提供了“取之不盡用之不竭”的教學資源.教學時應充分發揮引導作用，用巧妙的提問引導學生思考和探究，進而提升學生的數學核心素養，讓“生本課堂”成為數學課堂的常態.