拓展思維 提升素養
摘要:在課堂教學中培養、發展和拓展學生的數學思維,就是教會學生用數學的觀點去思考和解決問題,從而發展和提高數學核心素養.文章研究者結合“實際問題與一元一次方程(1)”的教學,闡述如何拓展思維、提升素養深度.
關鍵詞:數學思維;一元一次方程;實際問題
數學學科從本質上來說是一門“教思維”的學科,培養、發展和拓展學生的數學思維,就是教會學生用數學的觀點去思考和解決問題,從而發展和提高數學核心素養.對于一節課而言,問題情境的創設是著力點,可以啟發學生的數學思考,引領學生經歷思維探究的過程,從而有效拓展數學思維.
下面,以“實際問題與一元一次方程(1)”的教學為例,從學生的思維起點著手,深度剖析教學環節,以問題探究過程呈現學生的思維歷程,培養學生的抽象思維、類比思維、有序思維及創新思維,提高數學核心素養[1].
環節1情境導入,興趣盎然
背景:“新學期,新氣象”.為了給每個同學營造一個良好的學習環境和鍛煉的機會,全校準備開展一次大掃除活動.若按照以往的分工方法,初一(1)班是將全班分成2個小組,甲組26人打掃包干區,乙組22人打掃教室.但這次由于教室需要深度清潔,因此乙組的人數需是甲組的2倍,那么該如何分配?
學生獨立思考.
師:同學們,你們覺得應該如何表示甲組和乙組的人數及其關系呢?
生1:我覺得可以用x表示甲組的人數,那么乙組的人數就是2x.
師:很好,這是一個很好的代數表達方式.那么,根據題意我們能得到關于x的什么代數式呢?
生2:利用重新分配前后的總人數相等,可以得到一個關于x的等式.
師:這個想法很好,誰愿意分享一下你的成果?
生3:我認為如果甲組現在有x人,乙組就是2x人,那么可以得到x+2x=26+22這個等式,解得x=16,所以甲組是16人、乙組是32人.
師:有什么要補充的嗎?這是最終答案嗎?
生3:哦,這個不是最終答案,這是分配后的人數,題目問的是怎么分配,答案應該是將甲組的10人分配到乙組.
師:很好!這是最終答案.通過剛才的討論,可以看出這是一個一元一次方程的應用問題.今天我們就來學習如何建立并求解這類問題.
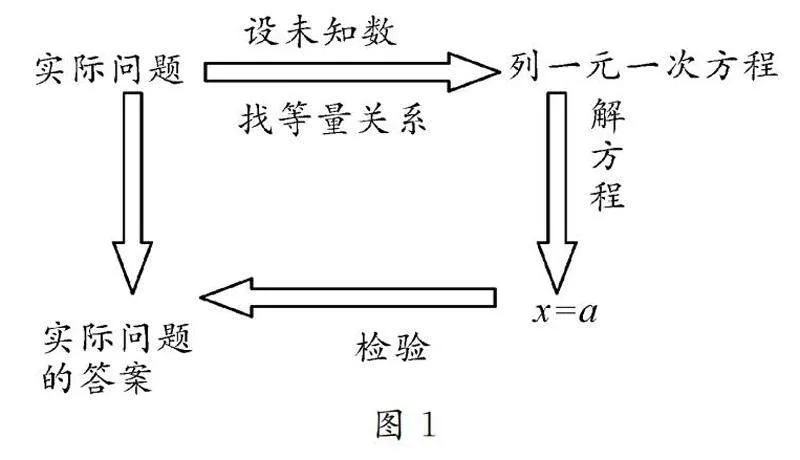
接下來結合圖1講解這類應用題的求解過程,并重點指出:設未知數和找等量關系是列方程的突破點,未知數的設法不同或等量關系不同,所列的方程就可能不同.盡管方程不同,但都可以通過解方程得到實際問題的最終結果.
評析:教學中我們需激發學生的好奇心、求知欲,促使學生積極主動地參與到數學探究中,自主自發地探尋解決問題的途徑.這里,教師結合現實生活創設的問題情境極好地激起了學生的學習動機,讓學生在簡單的數量關系探尋中體會成功的快樂,從而切實感知到“方程這個有效模型是對現實世界數量關系的刻畫”,為后續的思維活化做足準備.
環節2漸深探究,有效生成
繼續以設置的背景來引導學生思考.
教師追問1:仔細審題,看看你還可以怎么設未知數或列出不同的方程.
學生思考并討論,但沒有新結果.
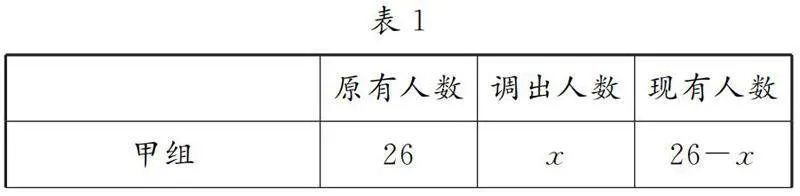
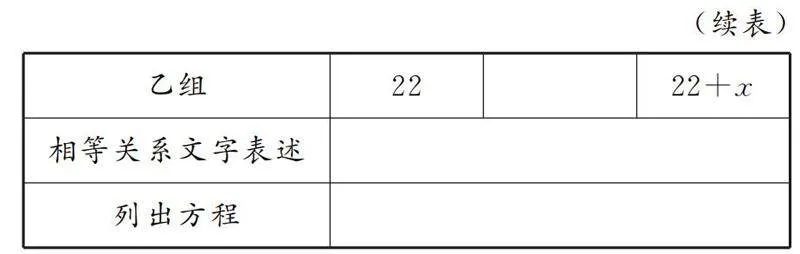
教師追問2:剛才我們通過間接設法來轉化問題求解,現在若設從甲組調出x人去乙組,你能把表1填寫完整嗎?
生1:相等關系可以是“現乙組人數=現甲組人數的2倍”.
生4:我可以列方程為22+x=2(26-x).
評析:大量研究表明數學思維常常無法主動發生,這就需要教師為學生的數學思考提供素材,使學生在引導性材料下深度思考,有效生成.這里,教師適時追問,為學生提供漸深探究的素材和自主探究的時空,讓學生在自主解題的過程中感受設元的多樣性.
問題背景:某初中初一年級(1)班有45人,(2)班有39人.近期學校打算排一個合唱節目,打算從(1)班和(2)班選拔部分學生參加排練.若(1)班比(2)班多選拔了1人,則(1)班剩余人數剛好是(2)班剩余人數的2倍,(1)班選拔了多少人?(2)班呢?
師:你得到了哪些數量關系?還有沒有隱藏的數量關系?怎樣用代數表達式表示這些數量關系?
生5:(1)班選拔人數=(2)班選拔人數+1.
生6:(1)班剩余人數=(2)班剩余人數×2.
師(追問):還有嗎?誰還發現了其他數量關系?
生2:(1)班選拔的人數+剩余人數=45.
生7:(2)班選拔的人數+剩余人數=39.
師:顯然,這一題的數量關系更加復雜了,有沒有好方法可以幫助我們厘清這些數量關系?
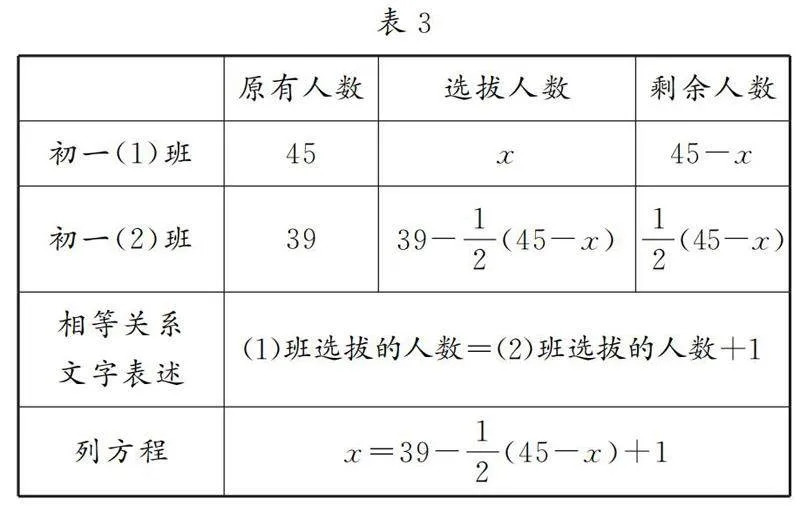
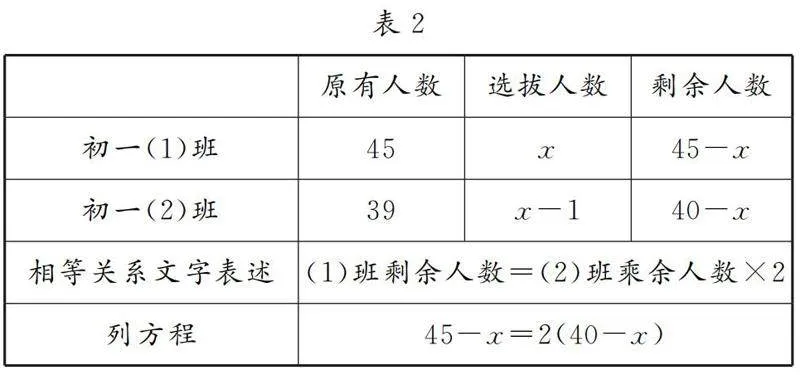
有了前面的探究經驗,學生很快提出“設未知數,制表格”的策略,生成表2與表3.
評析:這個問題也是人員調配問題,只是數量關系越發復雜起來,盡管學生可以輕松找到解題的策略,但找出等量關系是需要深入思考的.有了前面列表的經驗,學生很快就能完成數量關系的建立,在構建方程的基礎上凝練思維.
環節3課堂練習,拓展認知
問題設計:初一(1)班負責打掃實驗樓的有27人,負責打掃包干區的有19人.由于打掃任務繁重,現從外班調20人加入打掃,使得打掃實驗樓的人數是打掃包干區人數的2倍,那么往實驗樓、包干區各調了多少人?
師:請各位同學先獨立思考并解答問題.
學生思考并解答.
師:請各自小組成員互相討論自己的解決方法和答案.
學生開始分組討論并展示討論結果.討論結束后,教師總結問題的解答過程和結果,并重點強調建模的重要性和解題方法的靈活性,確保學生理解調配人數的具體過程和數學模型的建立,幫助學生鞏固相關概念.
評析:課堂練習活動的主要目的在于有效突破本節課的重點和難點,幫助學生切實掌握本節課的關鍵點,從而讓教學目標落到實處.這里,教師以一個變式問題引導學生深度探究,一方面為了檢測學生的學習成果,另一方面則是為了讓學生完整體驗解決問題的全過程,以達到深化理解和發展思維的目的.
環節4課堂小結,升華認識
教師提出問題,讓學生分組討論并整理用一元一次方程解決實際問題的步驟.
…………
評析:教學中的課堂小結看似簡單,實則不可忽視.巧妙而適當的小結可以幫助學生厘清知識結構,形成更加清晰的思路,進而構建屬于自己的知識結構體系.這里,教師又一次引領學生共同構建知識框架,從而培養學生的抽象能力和反思能力.
總之,數學課堂教學的目的不僅在于知識技能的獲取,還在于數學思維的開發與鍛煉,我們唯有做到著眼整體、深入鉆研、合理安排、巧妙設計、充分讓學,才能最大限度地開發學生的創新思維、抽象思維等.只有這樣,我們的教學才能達到應有的高度,學生才能在習得知識技能的同時拓展思維、提升素養.
參考文獻:
[1]郭靖.淺談小學數學教學中學生創新能力的培養[J].學周刊,2017(3):157-158.

