巧用幾何畫板，促進互動生成

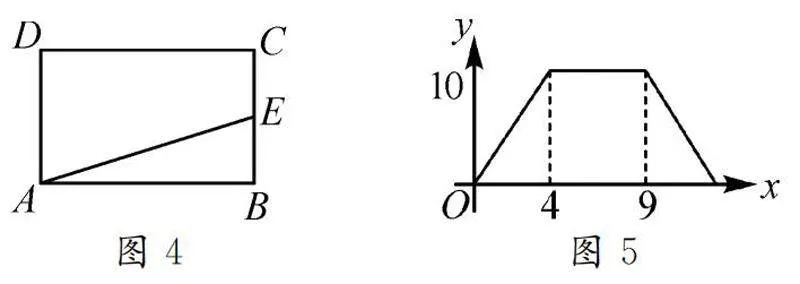
摘要：幾何畫板是一種繪制圖形和動畫展示的軟件，在數(shù)學(xué)教學(xué)中的應(yīng)用非常廣泛.借助幾何畫板學(xué)生能夠直觀地感受圖形的變化，從而形成更加清晰的認(rèn)識，構(gòu)建準(zhǔn)確的解題思路.本文中對利用幾何畫板體驗學(xué)習(xí)活動、構(gòu)建解題思路、促成互動交流進行探討，以提升學(xué)生的思維能力.

關(guān)鍵詞：幾何畫板;活動體驗;問題探究

數(shù)學(xué)學(xué)習(xí)以發(fā)展學(xué)生的核心素養(yǎng)為目標(biāo)，因此數(shù)學(xué)學(xué)習(xí)不能僅僅依靠機械記憶、被動接受、重復(fù)練習(xí)的學(xué)習(xí)方式，而需要在自主探究和操作實踐中不斷提升自己的認(rèn)知，深化知識理解[1].幾何畫板能夠動態(tài)展示圖形的變化，使抽象的圖形變得更加具體，為學(xué)生自主探究、合作學(xué)習(xí)提供更加直觀的學(xué)習(xí)資源.本文中以幾何畫板在教學(xué)中的使用為例，談一談運用幾何畫板加強師生互動、生成課堂智慧的教學(xué)策略，與各位仁交流.

1 注重活動體驗，探究概念性質(zhì)

數(shù)學(xué)活動是學(xué)生在實踐操作中進行觀察、分析、思考、探究的過程，通過數(shù)學(xué)活動的體驗，學(xué)生在實踐中發(fā)現(xiàn)問題，體會知識的生成和發(fā)展過程.數(shù)學(xué)概念和性質(zhì)具有抽象性和概括性的特征，幾何畫板的運用，為學(xué)生體驗數(shù)學(xué)活動提供了更加豐富的資源和便利的條件，使抽象的數(shù)學(xué)概念變得更加具體、直觀，強化了學(xué)生的體驗.

案例1運用幾何畫板探究旋轉(zhuǎn)概念

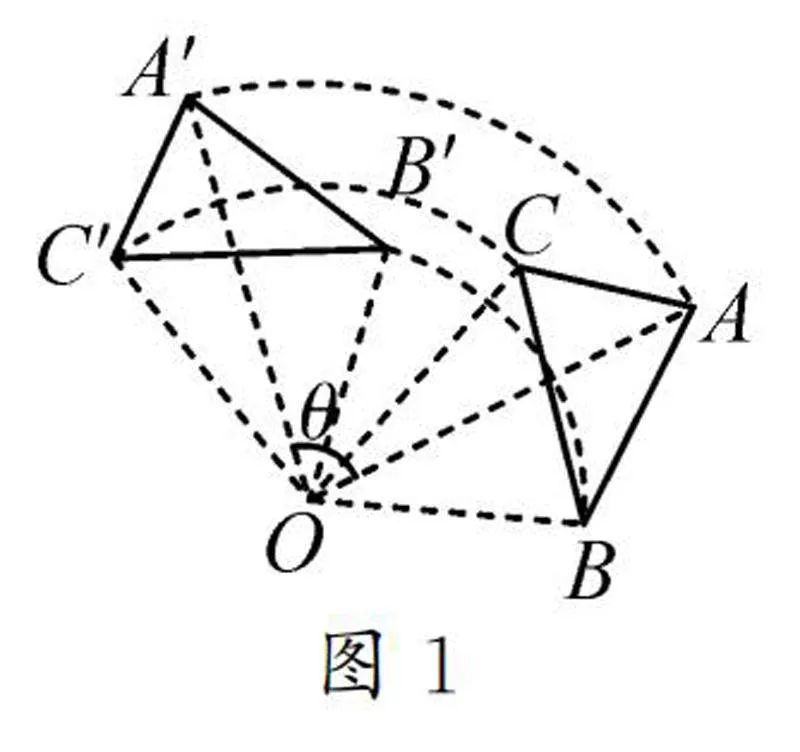
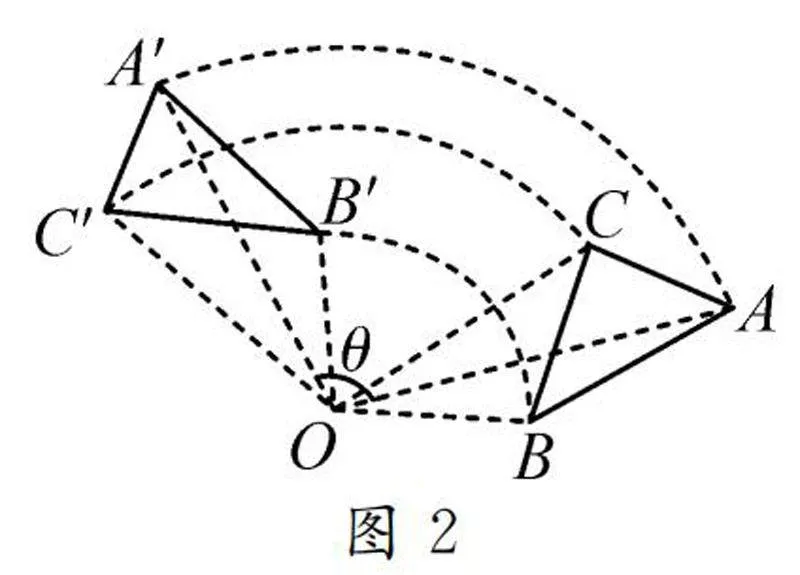
例1如圖1，打開幾何畫板，建立參數(shù)θ，將△ABC繞點O旋轉(zhuǎn)θ角度之后形成的△A′B′C′畫出來，標(biāo)上旋轉(zhuǎn)的中心點O.

問題1根據(jù)剛才的作圖過程，請你說一說什么是旋轉(zhuǎn).

生1：旋轉(zhuǎn)是指在一個平面內(nèi)，一個圖形圍繞固定的點進行一定角度的旋轉(zhuǎn)，從而改變原來圖形位置的過程.

師：很好！在旋轉(zhuǎn)的概念中，旋轉(zhuǎn)圍繞的固定點稱作旋轉(zhuǎn)中心，旋轉(zhuǎn)的角度稱作旋轉(zhuǎn)角.原圖中的點A在旋轉(zhuǎn)之后形成點A′，這兩個點稱作對應(yīng)點，如點B和B′、點C和C′都稱為對應(yīng)點.請大家運用幾何畫板分別測量出點A和A′、點B和B′、點C和C′到旋轉(zhuǎn)中心的距離，并將測量的結(jié)果記錄下來.

生2：圖1中，OA=OA′=8.07 cm，OB=OB′=5.18 cm，OC=OC′=5.96 cm；圖2中，OA=OA′=10.65 cm，OB=OB′=5.18 cm，OC=OC′=8.37 cm.我們可以看到無論三角形的形狀和大小如何變化，對應(yīng)點到旋轉(zhuǎn)中心的距離都是相等的.

師：非常好！這就是旋轉(zhuǎn)的第一個性質(zhì)，即對應(yīng)點到旋轉(zhuǎn)中心的距離相等.

師：下面我們研究對應(yīng)點與旋轉(zhuǎn)中心的連線形成的∠AOA′，∠BOB′，∠COC′之間的關(guān)系，請大家將度量的結(jié)果記錄下來.

生2：經(jīng)過測量，圖1中∠AOA′=∠BOB′=∠COC′=80°，圖2中∠AOA′=∠BOB′=∠COC′=100°.我們發(fā)現(xiàn)雖然三角形的大小和形狀不同，旋轉(zhuǎn)的角度也不同，但是對應(yīng)點與旋轉(zhuǎn)中心的連線形成的角度始終相等.

師：由此我們可以得到旋轉(zhuǎn)的第二個性質(zhì)，即旋轉(zhuǎn)對應(yīng)點與旋轉(zhuǎn)中心的連線形成的角相等.

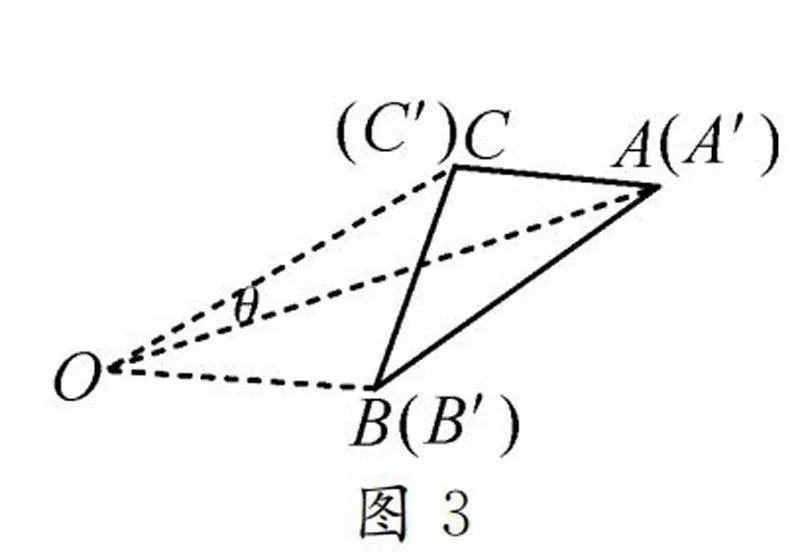
問題2當(dāng)我們改變旋轉(zhuǎn)角度θ，使得θ=360°，如圖3，這時△ABC和△A′B′C′完全重合，因此兩個三角形全等，請大家通過幾何畫板度量進行證明，并歸納旋轉(zhuǎn)的第三個性質(zhì).

生3：經(jīng)過度量可以得到圖3中AB=A′B′，AC=A′C′，BC=B′C′.因此，旋轉(zhuǎn)的第三個性質(zhì)是三角形在旋轉(zhuǎn)后形成的三角形與原圖形全等.

2 理清解題思路，感悟數(shù)學(xué)思想

數(shù)學(xué)思想是對具體數(shù)學(xué)問題進行的高度概括和提煉，體現(xiàn)了數(shù)學(xué)的本質(zhì)和規(guī)律.掌握數(shù)學(xué)思想方法是學(xué)習(xí)數(shù)學(xué)的目標(biāo)，通過數(shù)學(xué)學(xué)習(xí)學(xué)生能夠?qū)W會運用數(shù)學(xué)的眼光觀察問題，并在不同情境中主動進行知識遷移，提升解決數(shù)學(xué)問題的能力.在教學(xué)活動中運用幾何畫板引導(dǎo)學(xué)生進行合作探究，從而理清解題思路，并形成更高層次的抽象與概括，發(fā)展學(xué)生的思維品質(zhì).

案例2運用幾何畫板教學(xué)一次函數(shù)

例2如圖4，在矩形ABCD中，動點E沿BCDA的方向運動，直到點A處停止運動，設(shè)點E的運動路程和△ABE的面積分別為x和y，假設(shè)y關(guān)于x的函數(shù)圖象如圖5所示，判斷下列哪個說法是不正確的.

（1）當(dāng)x的值為2時，y的值為5.

（2）矩形ABCD的面積等于20.

（3）當(dāng)x的值為6時，y的值為10.

（4）當(dāng)y的值為15/2時，x的值為10.

解析：點E在矩形的三條邊上運動，要判斷以上結(jié)論是否正確，需要運用函數(shù)圖象進行解析.

第一種情況：當(dāng)0≤x≤4時，對應(yīng)圖5函數(shù)圖象中的第一段，此時，點E在矩形的BC邊上運動.利用幾何畫板拖動點E可知，△ABE的面積隨著點E的運動路程BE的增大而增大，當(dāng)點E到達點C時，x的值等于BC，△ABE的面積最大.根據(jù)函數(shù)圖象可以知道，y隨著x的增大而增大，當(dāng)x的值為4時，BC的值最大，等于4.因此，當(dāng)0≤x≤4時，一次函數(shù)的解析式為y=5/2x；當(dāng)x等于2時，代入可得y的值為5，因此，（1）是正確的.

第二種情況：當(dāng)4＜x≤9時，對應(yīng)函數(shù)圖象的第二段，這時點E在矩形CD邊上運動.根據(jù)圖象可知，y的值不變，即△ABE的面積不變，當(dāng)點E運動到到D點時，x=BC+CD=9，則DC=5.

根據(jù)BC，DC的值分別為4和5，可以知道矩形ABCD的面積為20.

當(dāng)4＜x≤9時，一次函數(shù)的解析式為y=10.當(dāng)x的值為6時，y的值為10.

因此，（2）（3）是正確的.

第三種情況：當(dāng)9＜x≤13時，點E在AD邊上運動.利用幾何畫板拖動點E可以發(fā)現(xiàn)，△ABE的面積隨著點E的運動路程x的增大而縮小，當(dāng)點E與點A重合時，x的值為BC，CD，DA的和，等于13，此時△ABE的面積最小.根據(jù)函數(shù)圖象可知，y隨著x的增大而減小，并且x等于13時，y的值最小，點E到點A時停止運動.

當(dāng)9＜x≤13時，函數(shù)的解析式y(tǒng)=5/2（13－x）=－5/2x+65/2.結(jié)合函數(shù)圖象可以知道，當(dāng)0≤x≤4和9＜x≤13時，兩段函數(shù)的函數(shù)值都有等于15/2時，即y的值等于15/2.當(dāng)y的值等于15/2，由5/2x=15/2或者－5/2x+65/2=15/2，可以解得x的值為3或者10，因此，（4）是錯誤的.

3 激發(fā)多維互動，生成課堂智慧

課堂教學(xué)是師生交流、生生交流的互動過程，有效的互動交流能夠活躍課堂氣氛，點燃思維火花，生成課堂智慧.幾何畫板的應(yīng)用為師生互動交流創(chuàng)設(shè)了更加廣闊的空間，提供了解決問題的多種途徑，從而發(fā)展學(xué)生思維的靈活性.

案例3運用幾何畫板探究平行四邊形中的相似問題

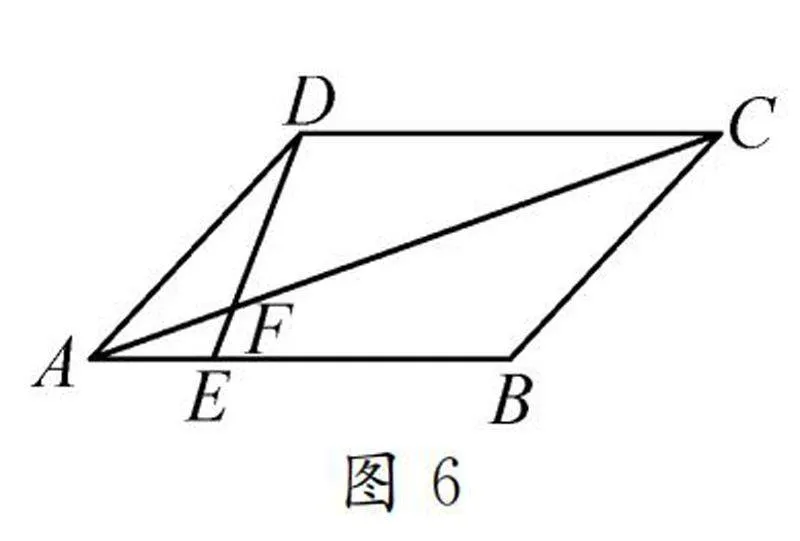
例3如圖6，平行四邊形ABCD中，AB上有一點E，AE/EB=1/2，DE與AC相交于點F，求AF∶FC的值.

（1）層層設(shè)問，深入挖掘

追問1：若△AEF的面積等于3，求△DCF的面積.

追問2：若△AEF的面積等于6，求△ABC的面積.

（2）變式練習(xí)，深化問題

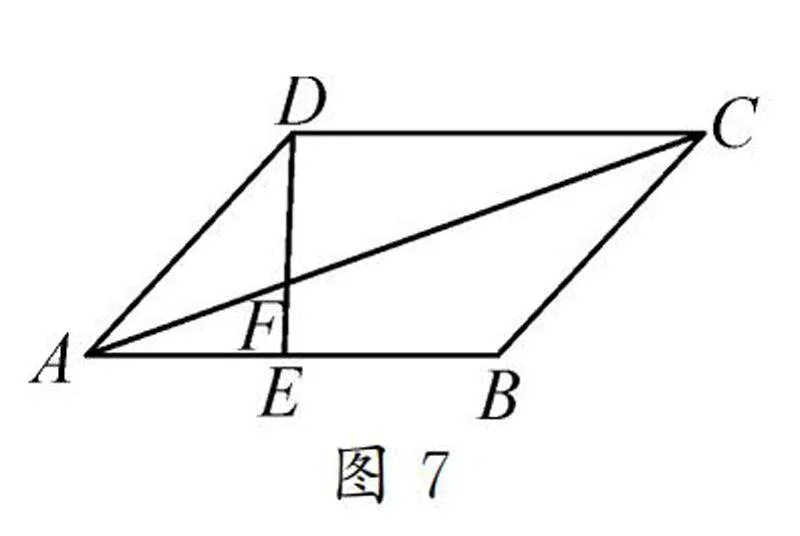
變式訓(xùn)練如圖7，平行四邊形ABCD中，AB的中點為E，DE與AC相交于點F.

問題1：求EF/DF的值.

問題2：若△AEF的面積為4，求△DCF的面積.

問題3：若△ADF的面積為9，求△DCF的面積.

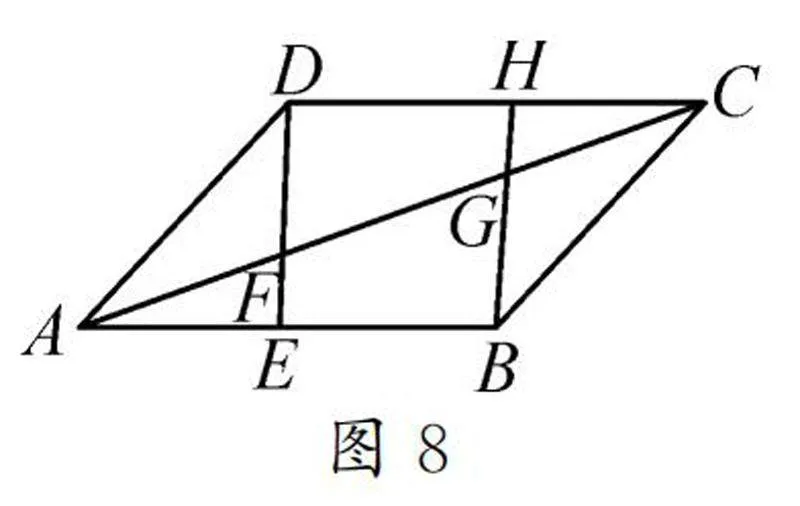
問題4：如圖8，過點B作BH與DE平行，BH與AC相交于點G，與DC交于點H，若AC的值為12，求FC的長度.

參考文獻：

[1]史寧中.數(shù)學(xué)基本思想18講[M].北京：北京師范大學(xué)出版社，2011.