“變”的教育價值

摘要：數(shù)學(xué)教學(xué)重在培養(yǎng)學(xué)生的思維，創(chuàng)造性思維的培養(yǎng)是教師創(chuàng)新教法的源動力所在.因此，教師的教學(xué)不能一成不變，而應(yīng)處于不斷改革創(chuàng)新中，是為“變”.“變”，教與學(xué)中無處不在.尤其是在核心素養(yǎng)理念深刻影響數(shù)學(xué)課堂教學(xué)的當(dāng)下，“變”正發(fā)揮著重要的教育價值.那么，何為“變”？為何“變”？如何“變”？將成為今后一段時間內(nèi)教師教學(xué)中常思考的幾個問題.

關(guān)鍵詞：“變”；教育價值；正方形；變式

要研究“變”的教育價值，首先要清楚何為“變”？粗略來講，“變”就是變化.在教育層面，“變”就是教育理念的變化；在教學(xué)層面，“變”就是教學(xué)方法的變化，即教法的改革與創(chuàng)新；在課堂實踐層面，“變”就是利用變式教學(xué)拓展學(xué)生的思維，讓學(xué)生的解題能力得到提升.其次，要清楚為何“變”？傳統(tǒng)的教學(xué)固化了學(xué)生的思維，不利于學(xué)生的全面發(fā)展.素質(zhì)教育背景下的數(shù)學(xué)教學(xué)要求教師打破傳統(tǒng)，勇于創(chuàng)新，因為“變”的教育價值體現(xiàn)在有利于培養(yǎng)學(xué)生科學(xué)思維能力、有利于提高學(xué)生的解決問題能力、有利于增強學(xué)生的自主探究能力等方面[1].最后，如何“變”？這才是“變”從理論到實踐的關(guān)鍵.

1 課前三思

北師大版九年級上冊第一章的最后一節(jié)安排了正方形的兩個課時內(nèi)容，分別介紹了正方形的性質(zhì)和判定.在介紹正方形的性質(zhì)時，先通過“議一議”引導(dǎo)學(xué)生初步感知正方形與菱形、矩形的區(qū)別，從而獲得正方形的兩個性質(zhì)定理（正方形的四個角都是直角，四條邊相等；正方形的對角線相等且互相垂直平分）.然后通過“想一想”激發(fā)學(xué)生的思維，并引導(dǎo)學(xué)生思考正方形的對稱性（軸對稱性：正方形是軸對稱圖形，有四條對稱軸；中心對稱性：正方形是中心對稱圖形，對稱中心是對角線的交點）.不難發(fā)現(xiàn)，這些都是進行正方形旋轉(zhuǎn)變式教學(xué)的基礎(chǔ).接下來，進行例1的講解與分析：

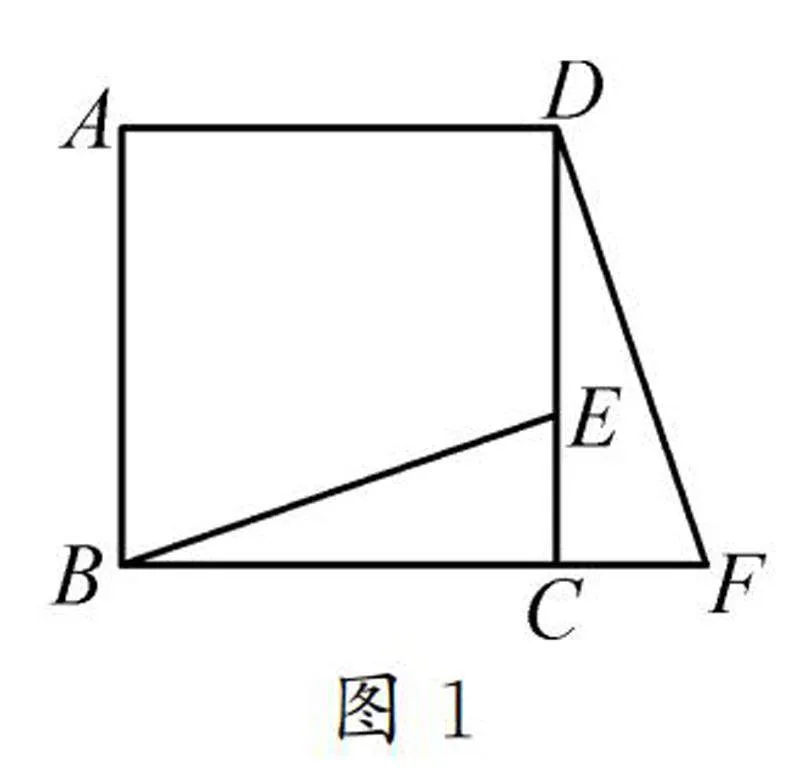
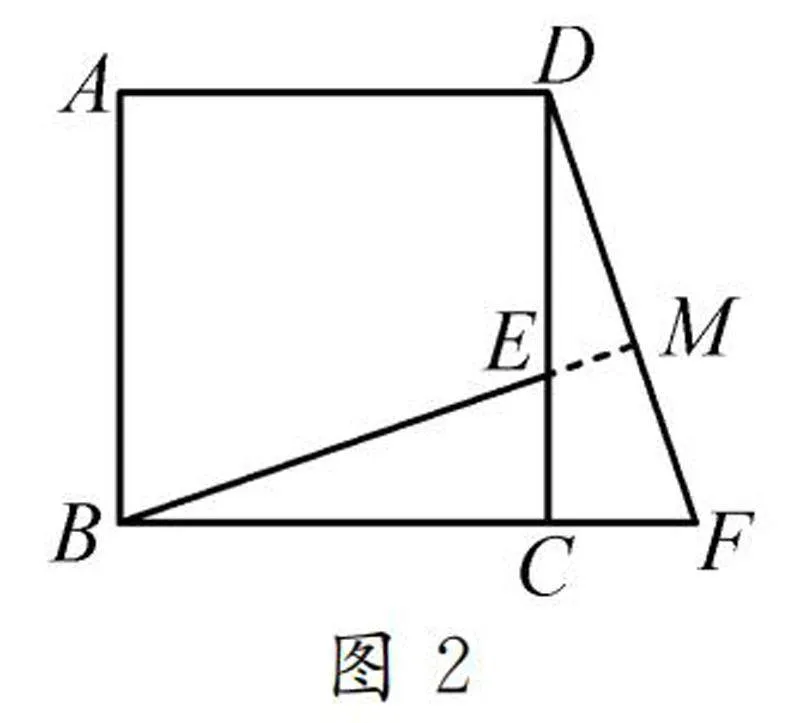
例1如圖1，在正方形ABCD中，E為CD邊上的一點，F(xiàn)為BC延長線上一點，且CE=CF.BE與DF之間有怎樣的關(guān)系？請說明理由.

看到該例題，筆者聯(lián)想到與其融合的旋轉(zhuǎn)問題.考慮到旋轉(zhuǎn)是解決該類問題的重要方法，同時當(dāng)前很多學(xué)生對旋轉(zhuǎn)的應(yīng)用不夠靈活，因此筆者對本節(jié)課的內(nèi)容進行拓展.于是進行了如下思考：

思考1除了借助例1傳授基礎(chǔ)知識和基本技能外，還可讓學(xué)生學(xué)到什么？

正如上述，本節(jié)課須在講解例1的基礎(chǔ)上進行拓展.觀察圖1不難發(fā)現(xiàn)，本題不僅可以用全等三角形解決，還可從旋轉(zhuǎn)這一角度入手.因此，本例題還可以讓學(xué)生進一步了解旋轉(zhuǎn)在正方形中的應(yīng)用.

思考2如何引導(dǎo)與銜接？

用旋轉(zhuǎn)解決問題，其思路主要是借助轉(zhuǎn)化思想.因此，在拓展時會面臨兩個問題：首先，如何引導(dǎo)學(xué)生進行變式？即“如何變？”其次，如何讓學(xué)生的思路在轉(zhuǎn)化前后實現(xiàn)有效銜接？筆者認為，這其實是“變法”與“解法”的問題，可分別從旋轉(zhuǎn)中心和旋轉(zhuǎn)圖形、旋轉(zhuǎn)的性質(zhì)入手（見教學(xué)過程）.

思考3如何提煉并應(yīng)用？

變式拓展教學(xué)的目的，不僅是為了激發(fā)學(xué)生的思維，也是為了讓學(xué)生提煉出“變”的方法及“變”后的解法.基于這一思考，筆者與學(xué)生在小結(jié)環(huán)節(jié)開展積極合作.

2 教學(xué)過程

2.1 常規(guī)解析

本例題主要是借助正方形的性質(zhì)判斷兩條線段間的關(guān)系，這種關(guān)系包括數(shù)量關(guān)系和位置關(guān)系，即BE=DF，且BE⊥DF.

解析：因為四邊形ABCD是正方形，所以BC=DC，∠BCE是直角，且易得∠DCF也是直角，故∠BCE=∠DCF.結(jié)合CE=CF，易證得△BCE≌△DCF，最終證得BE=DF.對于位置關(guān)系的判斷，先延長BE交DF于點M（如圖2）.因為△BCE≌△DCF，所以∠CBE=∠CDF.由∠DCF是直角，可知∠CDF+∠F=90°，所以∠CBE+∠F=90°，進而證得∠BMF=90°，故BE⊥DF.

2.2 激思變式

2.2.1 一問

師：剛才我們通過三角形全等證明了BE=DF，又通過角與角之間的關(guān)系證明了BE⊥DF.那么，有沒有其他的方法解決本題呢？

（學(xué)生經(jīng)過思考、討論，發(fā)現(xiàn)△DCF可以看成是△BCE繞著點C順時針旋轉(zhuǎn)90°形成的.）

生：老師，我發(fā)現(xiàn)△DCF和△BCE兩個三角形像是一種旋轉(zhuǎn)變化.

師：非常好！那么我們能根據(jù)旋轉(zhuǎn)解決本題嗎？

（學(xué)生發(fā)現(xiàn)思維“生長點”，并積極主動探索.）

評析：突破常規(guī)思維，引導(dǎo)學(xué)生仔細觀察，并鼓勵學(xué)生用自己的方式進行猜想，這正是變式拓展教學(xué)的前奏.只有學(xué)生突破了常規(guī)思維，才會產(chǎn)生不同的審題視角.這對促進學(xué)生發(fā)散性思維的形成與發(fā)展有利，同時也是后續(xù)變式拓展的基礎(chǔ).

經(jīng)過思考和探究，學(xué)生利用旋轉(zhuǎn)解決本題的思路大致如下：

首先，由BC=DC，CE=CF和∠BCE=∠DCF結(jié)合旋轉(zhuǎn)判斷出，△DCF可以看成是△BCE繞著點C順時針旋轉(zhuǎn)90°形成的.繼而，根據(jù)圖形旋轉(zhuǎn)的性質(zhì)“對應(yīng)邊相等”證得BE=DF.最后，同樣根據(jù)圖形旋轉(zhuǎn)的性質(zhì)得到BE與DF在旋轉(zhuǎn)過程中形成的角等于旋轉(zhuǎn)角，即BE⊥DF.

2.2.2 二問

師：既然△DCF是△BCE圍繞著正方形的頂點C旋轉(zhuǎn)而形成的，那么在正方形中還可以怎樣旋轉(zhuǎn)？

（該問一出，猶如一石激起千層浪，學(xué)生馬上投入到激烈的討論中.）

教師選學(xué)生代表談一談思路.

生1：我覺得是不是可以讓三角形旋轉(zhuǎn)后再翻折，得到△DCF關(guān)于DC的對稱三角形.

生2：我認為可以將△BCE換成一個正方形，讓該正方形繞著點C旋轉(zhuǎn).

生3：我還覺得可以讓這樣的正方形繞著正方形ABCD的中心旋轉(zhuǎn).

…………

師：大家的思路都很不錯，能不能根據(jù)自己的想法畫出圖形并給出一定的條件呢？

生：可以（畫圖）.

經(jīng)過一番操作，學(xué)生獲得了下面三個變式：

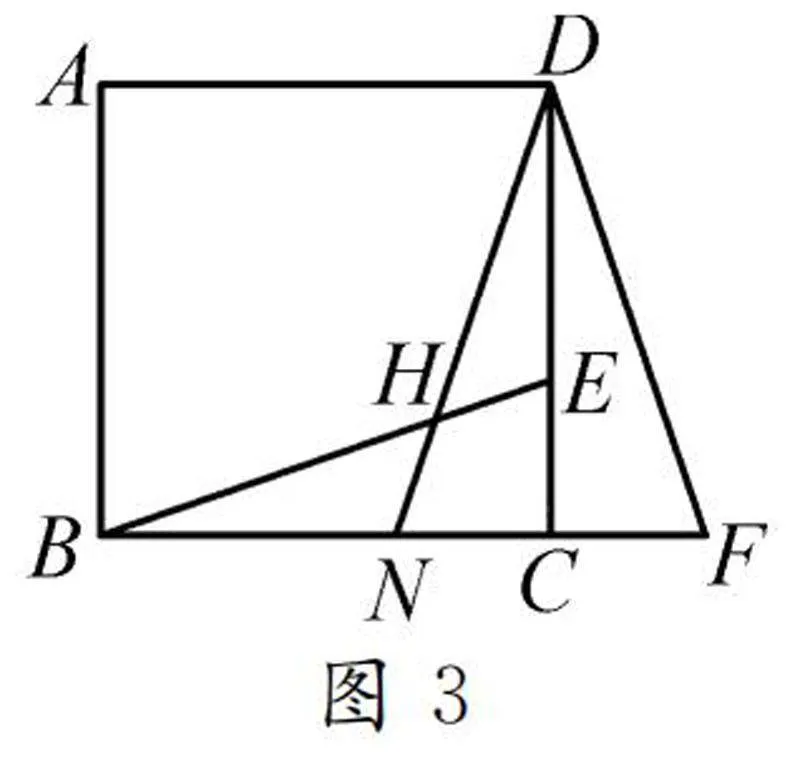
變式1如圖3，E是正方形ABCD邊DC上的一點，延長BC至點F，使CF=CE，連接DF.以DC為對稱軸作出△DCF的軸對稱圖形△DCN，DN與BE交于點H.你能找出全等三角形嗎？選擇其中一組給出證明.

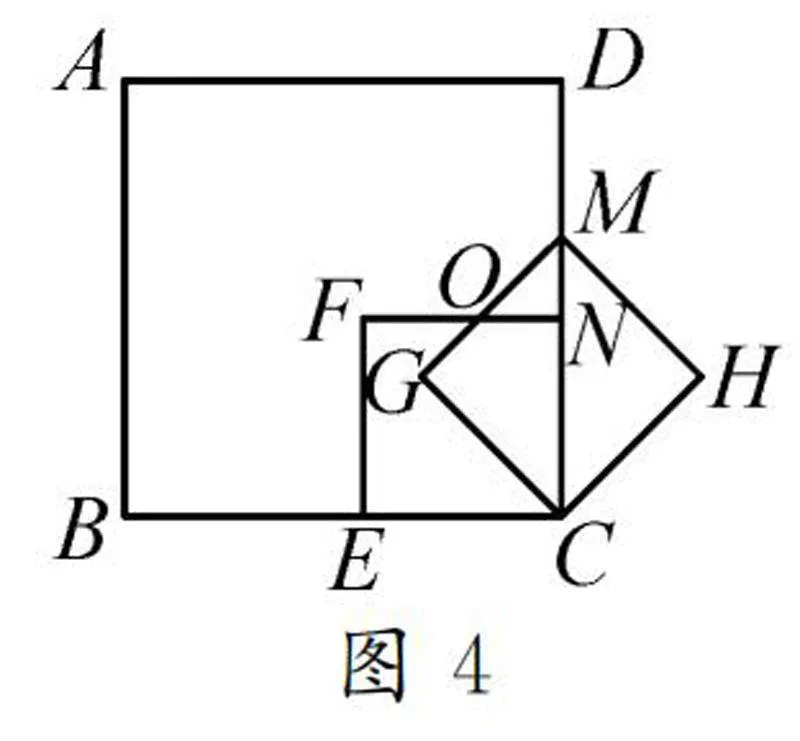
變式2如圖4，正方形ABCD的邊長為4.分別取BC，DC的中點E，N作正方形EFNC，并將其繞著點C按順時針方向旋轉(zhuǎn)45°得到正方形GMHC，F(xiàn)N交GM于點O，求ON的長.

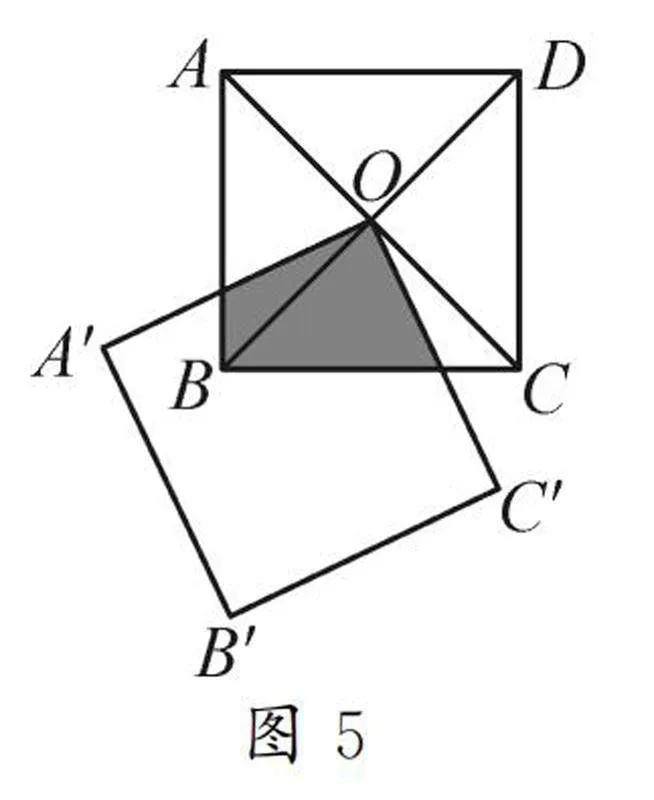
變式3如圖5，正方形ABCD的對角線相交于點O，正方形A′B′-C′O與正方形ABCD的邊長相等.當(dāng)正方形A′B′C′O繞著點O旋轉(zhuǎn)，兩個正方形重疊部分的面積是否會變化？如果不變，請計算出重疊部分面積與正方形ABCD面積之間的關(guān)系;如果有變化，請說明理由.

3 解題小結(jié)

在獲得變式以后，學(xué)生分組完成上述三個變式.這樣一來，不僅讓學(xué)生經(jīng)歷了變式產(chǎn)生的過程，而且通過解決自己設(shè)計的變式題，自信心得到提高.

“變”是創(chuàng)造性思維的源泉，讓學(xué)生“變”，既是解題習(xí)慣的“變”，也是解題思維的“變”[2].學(xué)生一改以往就題解題的學(xué)習(xí)方法，深入思考和探究獲得變式，不局限于一道題，不斷拓展.

總之，教師的教學(xué)不能一成不變，要在課堂活動中靈敏捕捉思維的“生長點”，并且激發(fā)學(xué)生自主探究，讓學(xué)生參與到變式教學(xué)中，不斷提高他們的思維能力和解決問題能力.

參考文獻：

[1]侯德森.變式教學(xué)貴在變之有道——以一道習(xí)題教學(xué)為例[J].中小學(xué)數(shù)學(xué)：初中版，2018（6）：1-3.

[2]張鋒.小題大做的教育價值——以一節(jié)正方形復(fù)習(xí)課的教學(xué)為例[J].中國數(shù)學(xué)教育，2020（19）：10-14.