回歸教材重探究,問題尋“多”顯素養
摘要:在初中數學解題教學過程中,我們往往忽視了教材中“典型問題”的探究,靠題海戰術進行強化訓練.本文中則針對教材中的典例,進行回歸探究,在探究一題多解、一題多變、一題多思的過程中,探索數學知識點的巧妙運用,體驗數學方法與思想的指導與融合,從而更好地提高學生解題能力,提升學生數學核心素養,真正落實“雙減”.
關鍵詞:初中數學;回歸教材;一題多解;一題多思;核心素養
《義務教育數學課程標準(2022年版)》中已經明確指出:確立核心素養為導向,以學生發展為本,進一步強調學生獲得數學“四基”,運用數學知識與方法發展“四能”,形成正確的情感、態度和價值觀,考查的問題必須以教材為基準點,立足教材,根據學生能力發展適度拓展,以信度、效度和區分度為基礎,以教師有效教學指導為導向,讓教材問題成為評價學生核心素養達成的重要載體.
1 教材原型試題呈現
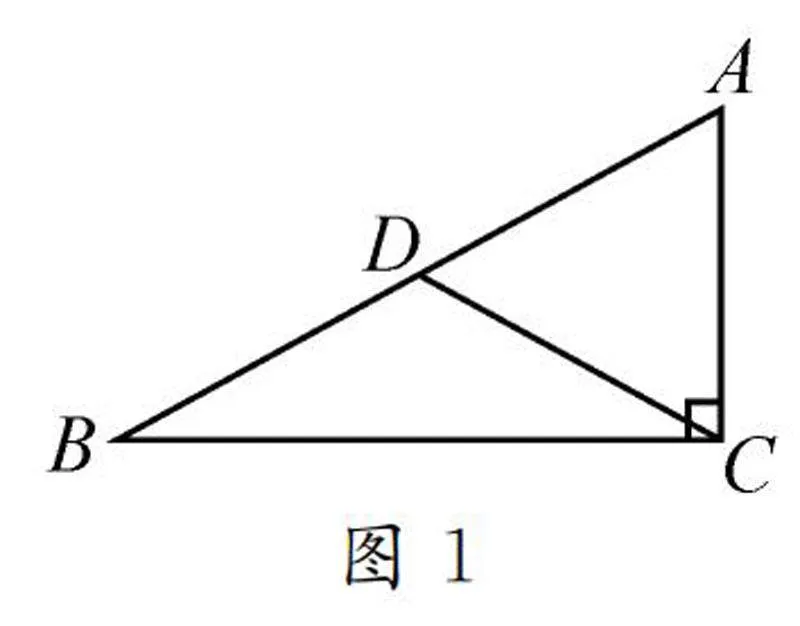
課本原型問題如圖1,畫Rt△ABC,并畫出斜邊AB上的中線CD,然后量一量,比較一下看看CD與AB的長度關系是怎么樣的.
通過測量,相信你會發現:CD恰好是AB的一半.下面讓我們用演繹推理證明這一猜想.
已知:在Rt△ABC中,CD是斜邊AB上的中線.
求證:CD=1/2AB.
2 回歸教材探究本質
多解多題歸一是培養學生數學思維聚合性的好方法、好思路,這就需要我們教師在教學過程中要抓住任何機會讓學生體現創造過程,從而感受發散思維和聚合思維完美融合的成功感與成就感.多解多題歸一就是針對這方面的專題訓練,雖然遇到的問題不會完全相同,但是卻能從“異”中探“同”,從“同”中尋“異”.面對我們所遇到的“型異質同”或“型近質同”等問題的探究分析,可從中提煉問題的本質特征,從而探尋問題存在的內在規律,做到解題舉一反三、觸類旁通、事半功倍.這既能體現“數學核心素養”培養目的,更能深入落實“雙減”政策,真正擺脫“題海”的累贅,做到輕松學習.
3 一題尋“多”提素養
3.1 一題多解提升素養
針對課本原型問題我們可以思考得到如下解法:
解法一:構造法.
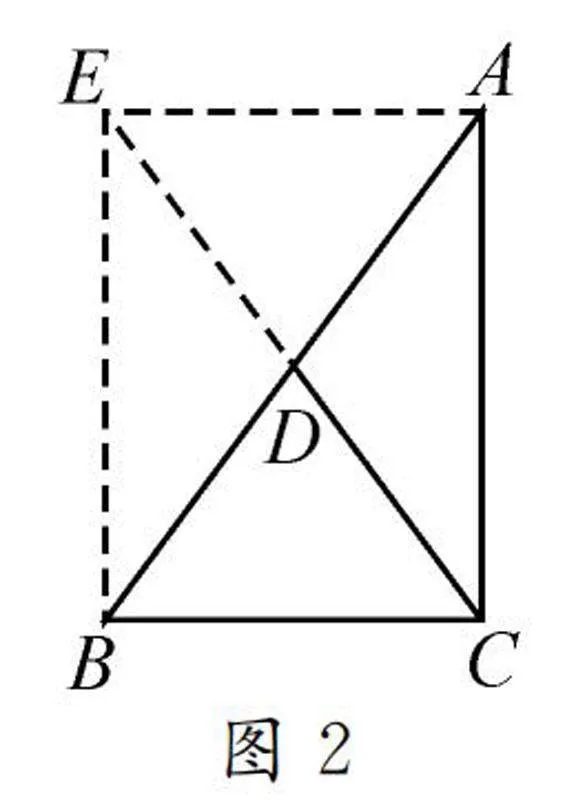
如圖2,延長CD到點E,使DE=CD,連接AE,BE,這樣可以得到CD=1/2CE.又CD是直角三角形斜邊AB上的中線,從而可得AD=BD,因此可以得到四邊形ACBE是平行四邊形.再結合∠ACB=90°,判斷得到平行四邊形ACBE是矩形.故CE=AB,即CD=1/2AB.
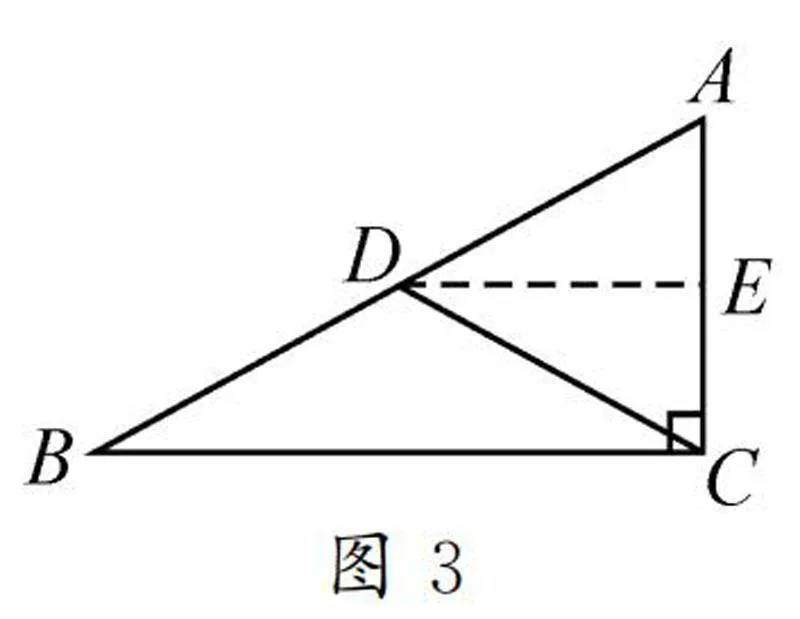
解法二:相似法.
如圖3,過點D作AC的垂線,垂足為E.因為∠ACB=90°,所以DE∥BC,則△ADE∽△ABC.因為D是AB的中點,所以AD∶AB=1/2,從而得到AE∶AC=1/2,即DE是AC的垂直平分線,則有AD=DC.故CD=1/2AB.
解法三:作角法.
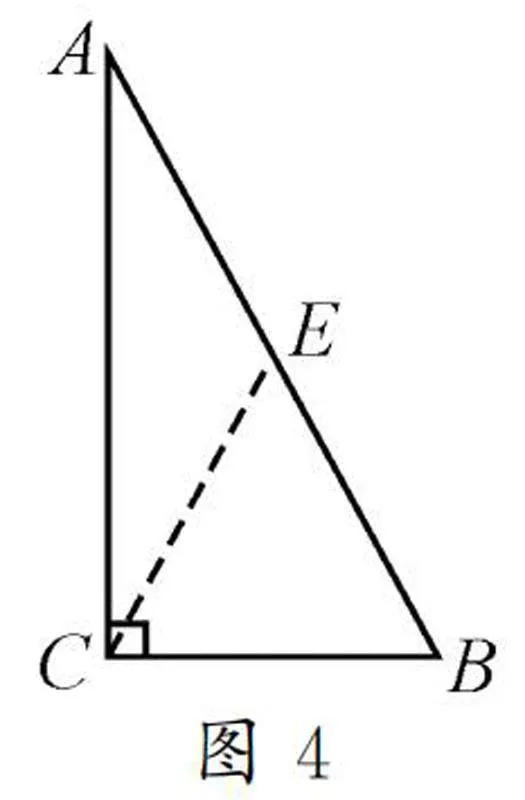
如圖4,在∠ACB的內部作∠BCE=∠B,CD與AB交于點E,則BE=CE.
又根據∠BCE+∠ACE=90°,∠B+∠A=90°,可得∠ACE=∠A,則EA=EC.故EA=EB=EC,即CE與CD重合,且CD=CE=1/2AB.
從上面的解法中我們可以發現,不同的方法著眼點不同,解題思路不同,所體現的數學基本知識也存在著差異.多種方法的體現也真正考查了學生對基本知識的掌握能力和運用數學知識的能力,從而起到提升數學核心素養的作用.
3.2 一題多變促進發展
例如,張老師指導學校數學興趣小組進行如下問題探究:
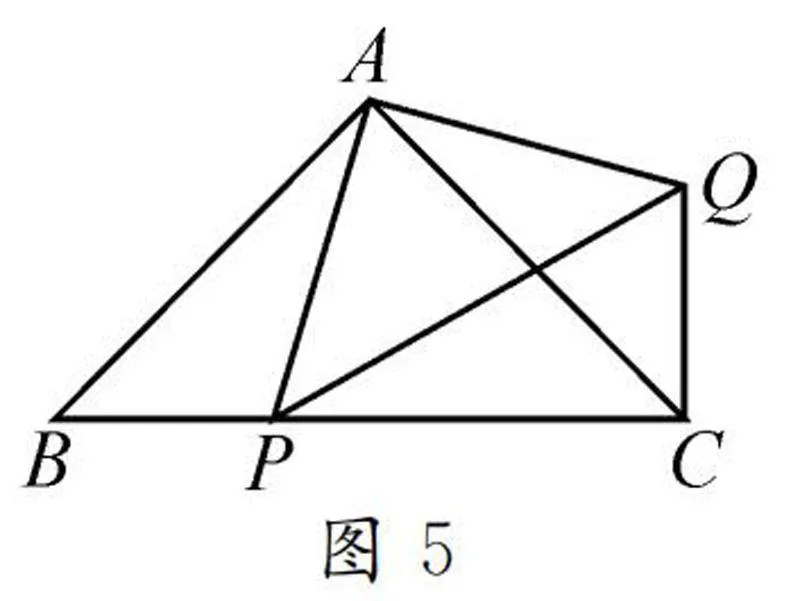
原型問題如圖5,在等腰直角三角形ABC中,∠BAC=90°,P是斜邊BC上一點,連接AP,以AP為腰作等腰直角三角形APQ,且∠PAQ=90°,連接CQ,判斷BP和CQ的數量關系.
解題思路:根據題意可以由∠BAC=90°=∠PAQ,得到∠BAP=∠CAQ,從而得到△ABP≌△ACQ,即可得出結論.
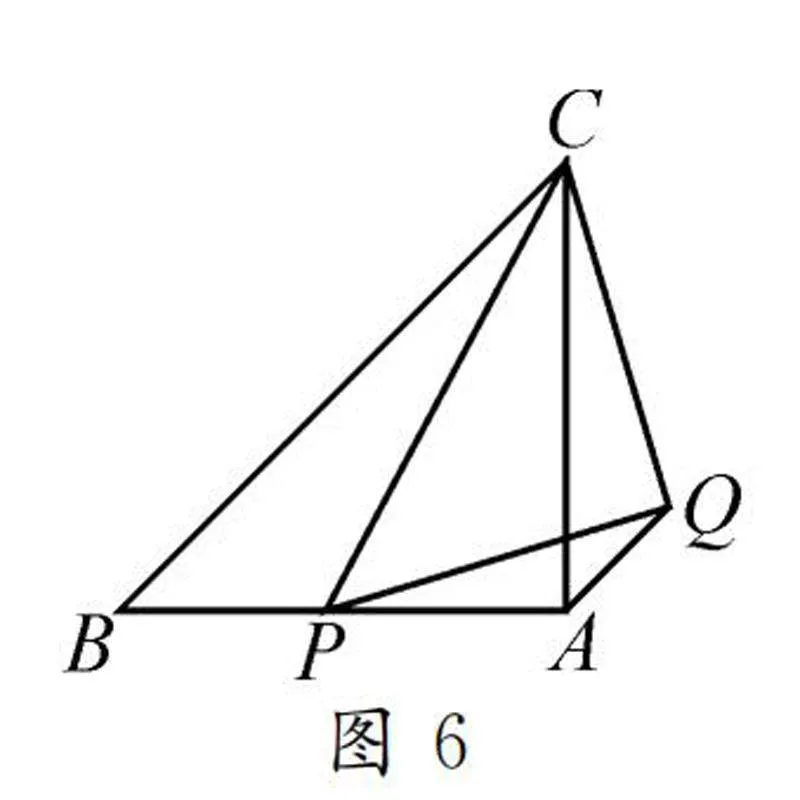
變式1如圖6,將原型問題中點P的位置由斜邊變化至某條直角邊上,連接CP,再以CP為底邊作等腰直角三角形CPQ,連接AQ,判斷BP和AQ的數量關系.
解題思路:由題意得∠PCQ=45°=∠BCA,則可判斷出∠BCP=∠ACQ,再判斷出BC/AC=CP/CQ=2,得到△BCP∽△ACQ,即可得出結論.
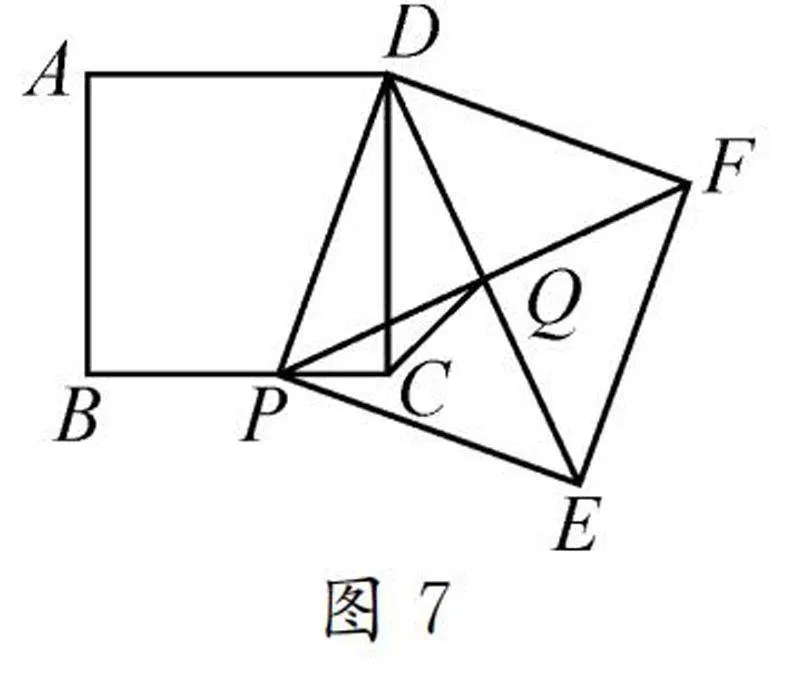
變式2如圖7,如果將原型問題中的等腰直角三角形轉化為正方形ABCD,在邊BC上有一點P,再以DP為邊作正方形DPEF,其中心為點Q,連接CQ,判斷DP,CQ和CD之間的關系.
解題思路:根據圖形的特點,易得出BP=2CQ,從而再根據兩個正方形邊長與其關系利用勾股定理建立方程求解,即可得到答案.
綜合上述變式可知,針對同一個問題,我們可以在位置和圖形形狀上進行變化,解答過程中涉及的知識點也隨之變化,一題多變讓學生在解答過程中充分得到思維的發散,問題的求解讓知識點充分展示出來,數學核心素養從而得到提高.
3.3 一題多思深挖思想
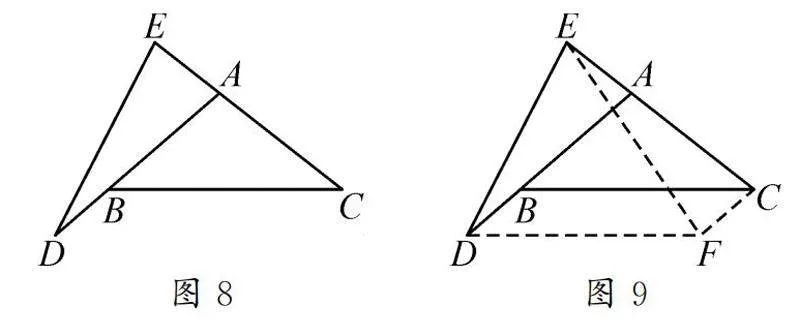
問題展示如圖8,在等腰三角形ABC中,AB=AC,延長CA至點E,延長AB至點D,使得BC=CE=DE=AD,試求∠BAC的度數.
解題思路:由題意發現,相等的四條邊形成一個凹形四邊形,根據我們所學知識點,很難將這些條件進行巧妙運用.這就需要進行變化,故可思考將BC平移至DF處,如圖9,連接CF,自然構成了平行四邊形,再根據平行四邊的性質可得BD=CF,DA∥FC,則∠EAD=∠ECF,利用“SAS”判定△ADE≌△CEF,所以ED=EF,從而可推出△DEF為等邊三角形.設∠BAC=x,則∠ADF=∠ABC=180°-x/2,根據三角形內角和定理可分別表示出∠ADE,∠ADF,根據等邊三角形的性質不難求得∠BAC的度數.
從上面的問題我們可以思考得到:其一,利用平移變換將相等的邊轉移在同一個三角形內,構造特殊三角形,便于利用相關條件進行解答;其二,針對相等的邊所對應的三角形構造全等形,利用全等三角形的性質進行邊、角的轉化,形成問題突破點;其三,整個問題條件中沒有涉及到角度,但求的是角度,這就需要我們利用角度之間的關系,建立方程,進行解答,特別是出現角度之間的倍數關系時也要注意利用方程思想來突破.
綜上所述,不管是一題多解、一題多變,還是一題多思,都是在教學中注意指導學生不斷領會數學問題中所體現的思想,訓練思維品質,更是借助“多”的思考培養學生的發散性思維,激發學生學習興趣,培養思維的靈活性,從而更好地促進學生數學核心素養的提升.
4 多解歸一激活思維
多題歸一的訓練,達到使學生鞏固與深化所學知識,提高解題技巧及分析問題、解決問題的能力,增強思維的靈活性的目的.通過訓練,學生達到對知識認識的全面性.同時,還要重視解題反思,形成系統化認識.通過反思,引導學生回顧概括數學結論的整個思維過程,檢查得失,從而加深對數學原理、通性通法的認識;通過系統化,建立新知識與已有認知結構中相關知識的橫向聯系,井概括出帶有普遍性的規律,從而推動同化、順應的深入.這樣的教學方法有利于培養學生思維的靈活性,增強應變能力.
問題探究是解決數學的關鍵,方法指導是數學突破的手段,思想利用是解決問題的靈魂所在.我們借助教材中的典型例題進行“多元”突破,讓數學問題、數學知識、數學方法、數學思想進行巧妙融合,形成相互影響、相互聯系和統一發展的辯證統一體,讓問題解答過程中所體現的內在關系得到充分的展示,靈活體現問題的“多元化”,讓學生能力得到提高、數學核心素養得到提升.

