初中數學課堂教學生成性資源開發和利用

摘要:本文中以“角的平分線的性質”為例,陳述了利用往屆數學課堂的生成性資源進行教學設計,通過設計情境引導學生經歷角的平分線的性質和角的平分線的尺規作圖方法的再生成過程.
關鍵詞:生成性資源;初中數學;課堂教學
《義務教育數學課程標準(2011年版)》在實施建議部分提出:“生成性資源是在教學過程中動態生成的,如師生交互及生生交流過程中產生的新情境、新問題、新思路、新方法、新結果等.合理地利用生成性資源有利于提高教學的有效性.”[1]生成性資源主要是指初中數學課堂教學中生成的課程資源,它是依托數學課堂教學過程,通過師生之間、生生之間的交互產生的.生成性資源是動態的,有教師預設中的生成,也有超出預料范圍之外的生成[2].下文以“角的平分線的性質”第1課為例進行說明.
1 利用資源,前置避錯
學生的學習錯誤是一種生成性資源.教學中教師應把握數學學習錯誤的規律,揭示數學學習錯誤的成因,適當加工數學學習錯誤,挖掘數學學習錯誤的資源性價值[3].課本以文字敘述的形式給出了角的平分線的性質:角的平分線上的點到角的兩邊的距離相等.證明該性質時,需要分清其題設和結論.往屆學生學習錯誤記錄表明:部分學生把“距離”放在結論中,部分學生忽略“點到直線的距離”中隱含著“垂直”的條件,還有部分學生漏了“點在(角平分)線上”,這都導致了符號化的過程出現障礙.為幫助學生順利跨越該障礙,實施以下教學環節:
1.1 復習鞏固,激活記憶
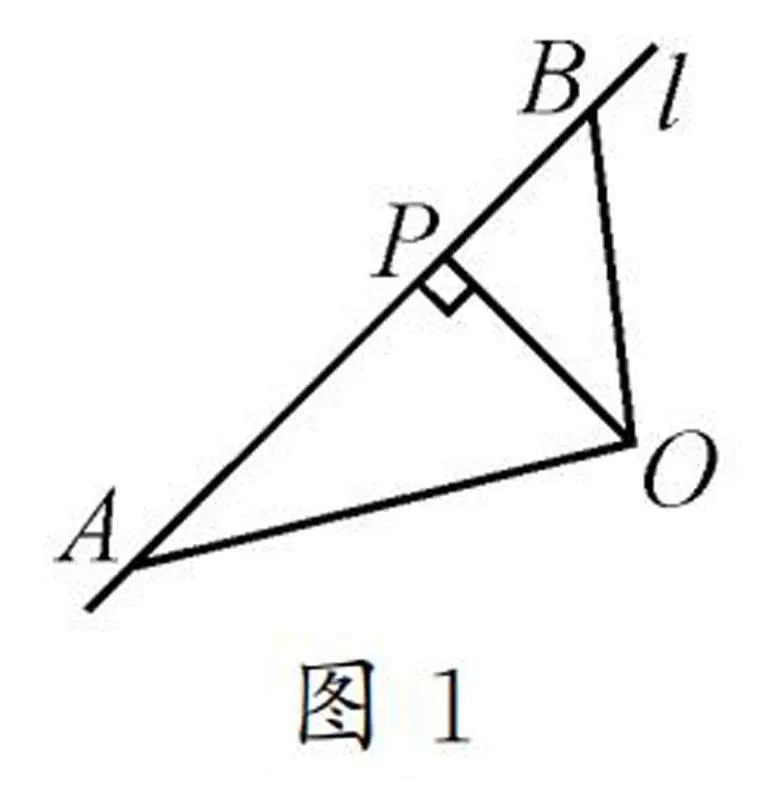
設置課前復習,積累“點到直線的距離隱含垂直的位置關系”的經驗,激活長時記憶,促其生成表象,達成前置避錯.圖1
填空如圖1,點O到直線l的距離是線段____的長度.
教師個別提問后板書:“點O到直線l的距離可表示為OP⊥l于點P”強調距離隱含著垂直,點到直線的距離的符號語言中必須交待垂足.
1.2 目測實驗,強調題設
問題1分組實驗:
學號為奇數的學生做實驗A,學號為偶數的學生做實驗B.實驗結束后,學生交流由實驗所得的猜想,再用幾何畫板驗證猜想.
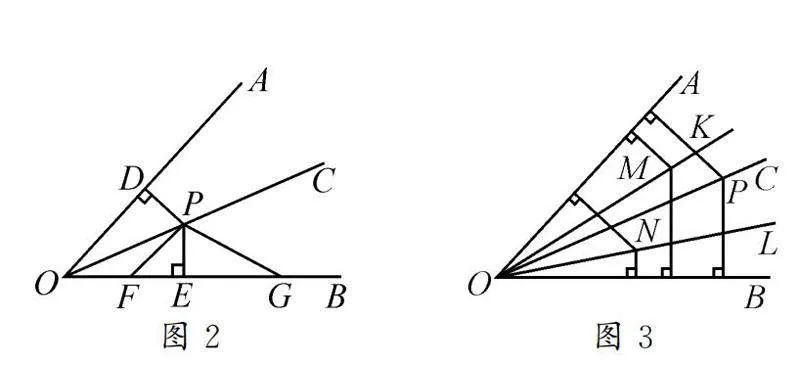
實驗A如圖2,OC平分∠AOB,點P在OC上,PD⊥AO,PE⊥OB,垂足分別為D,E,點F與G在OB上.
目測:四條線段PD,PE,PF,PG中,____=____.
實驗B如圖3,OC平分∠AOB,點P,M,N分別在OC,OK,OL上,分別過點M,P,N作OA,OB的垂線段.
目測:三組共端點的垂線段中,兩條線段的長度相等的是____.
猜想:____.
目測實驗后,學生順利得出猜想.在此過程中,通過實驗A強調“到兩邊的距離”,通過實驗B強調“點在角平分線上”.在學生完成猜想后,標記三個條件:“角平分線”“點在角平分線上”“到兩邊的距離”,如圖4:
往屆課堂教學的生成性資源是當下課堂教學的重要資源,值得教師們深入分析其成因,并充分發揮其資源性價值.
2 觀察操作,自主生成
多爾(WILLIAME.DOLL)認為,學生應該從“做中學”,生成知識,轉化經驗,生成不可預知的因素,碰撞出創造的火花,新的知識就這樣產生了.課堂“活”起來,學習才是有生命力的[4].筆者讓學生經歷目測感知→操作體會→歸納猜想→推理證明,實現知識的再生成過程.
2.1 目測感知
目測實驗讓學生在處理視覺刺激和語言刺激的過程中,自發地猜想出角的平分線的性質,并用提出猜想的學生姓氏命名(如:雷氏猜想),讓學生體會成功的同時,明確猜想的三個條件.
2.2 操作體會
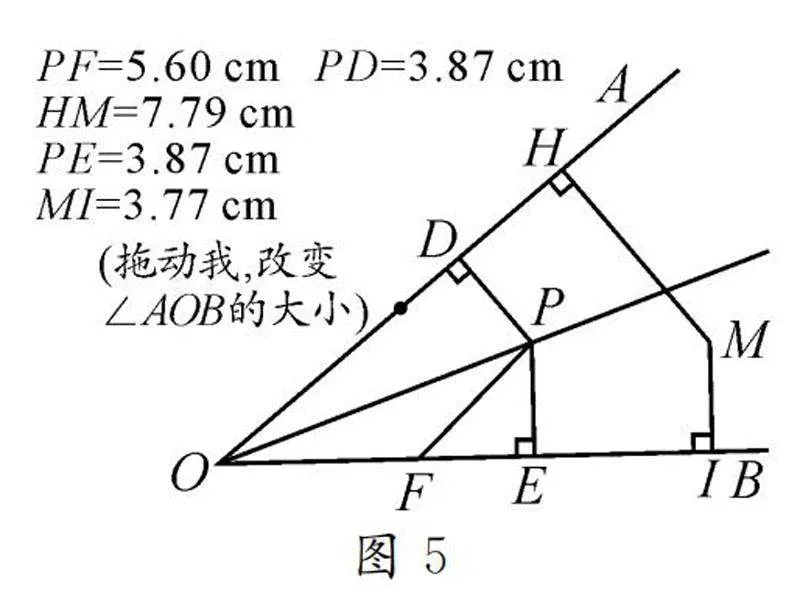
圖5為了能更深入地理解命題的內涵,讓學生經歷幾何畫板操作實驗(如圖5),并回答:①你拖動了哪個點?②你觀察了哪些數據?③實驗后你得到了怎樣的結論?
設計意圖:讓學生通過操作實驗,進一步領悟猜想的內涵.改變點M的位置,觀察HM和IM的大小變化,進一步強化“點在角的平分線上”的條件.改變點F的位置,觀察PF和PD的大小關系,進一步強化“點到角的兩邊的距離”的條件.改變點P的位置,觀察PE和PD的大小關系,讓學生體會命題對于角平分線上任意一點都成立.拖動點D,改變∠AOB的大小,讓學生領悟命題對任意大小的角都成立.
2.3 推理證明
追問1:經歷實驗驗證,猜想一定成立嗎?為什么?
當時,所有學生表示不成立.但是說不出為什么.還有一位李同學舉手回答“一定成立”并口頭證明了命題.在學習三角形內角和定理的過程中,積累了一定的從實驗幾何走向論證幾何的數學活動經驗.這說明學生還沒真正領悟證明的必要性.學生的回答得到肯定后,教師再講述證明的必要性,帶領學生從實驗幾何走向論證幾何.
追問2:角的平分線的性質中,題設和結論分別是什么?點到直線的距離隱含著什么條件?
用符號語言寫出已知和求證,讓李同學再陳述一次證明過程,教師板書,把用全等三角形證明線段(或角)相等的思路稱為“李氏思路”.學生經歷觀察、歸納、猜想、實驗驗證、推理論證過程,體會研究幾何問題的基本思路.
2.4 類比遷移
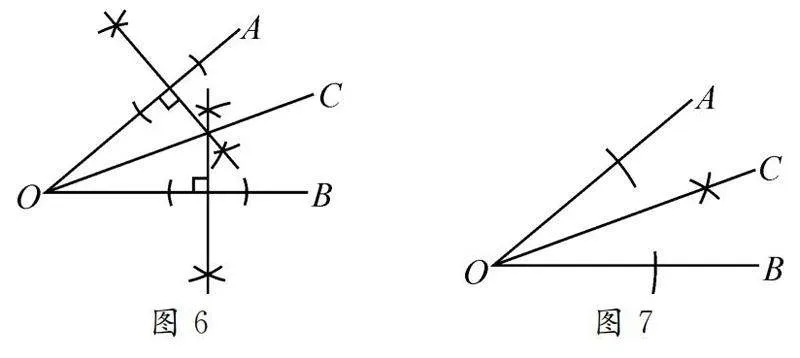
“用‘李氏思路’還可以找到角平分線的尺規作圖方法.”如圖6,已知∠AOB,請用盡可能多的方法作出∠AOB的角平分線.(要求用尺規作圖.)
設計意圖:引導學生借用“李氏思路”,遷移生成作角平分線的尺規作圖方法.
學生展示學習成果,如圖6、圖7.
追問1:方法可行嗎?(要求學生口頭證明作圖方法,養成有理有據的推理習慣,提高推理能力,培養實事求是的科學精神.)
追問2:哪種方法更簡便?(利用類比,引導學生自主生成優化策略,體現數學的簡練之美.)
3 體驗成功,自主內化
課堂總結時,學生驕傲地回答:“這節課我們學習了雷氏性質、李氏思路和角的平分線的尺規作圖方法.”用學生的姓氏命名定理和通性通法,激發學生的學習積極性,誘發學生自主內化.
讓學生經歷數學觀察、數學思考、數學表達、概括歸納、遷移運用等學習過程,體會數學是認識、理解與表達現實世界的工具、方法和語言,增強認識現實世界、解決現實問題的能力,樹立學好數學的自信心,養成良好的學習習慣[5].
參考文獻:
[1]中華人民共和國教育部.義務教育數學課程標準(2011年版)[S].北京:北京師范大學出版社,2012:67-71.
[2]雷珮瑛.知惑教學[M].廣州:華南理工大學出版社,2021:6.
[3]雷珮瑛.知惑教學[M].廣州:華南理工大學出版社,2021:7-8.
[4]羅祖兵.生成性教學的基本理念及其實踐訴求[J].高等教育研究,2006(8):47-53.
[5]中華人民共和國教育部.義務教育數學課程標準(2022年版)[S].北京:北京師范大學出版社,2022:87.

