探究式教學在數學教學中的應用

摘要：探究式教學是在“以生為本”的基礎上，踐行“立德樹人”教育理念的一種教學方式.文章以“二次函數的認識”教學為例，分別從“舊知回顧，思維熱身”“創設情境，引發探究”“練習訓練，辨析概念”“應用概念，完善認知”“課堂總結，拓展延伸”五個環節展開探究式教學，并談一些思考.

關鍵詞：探究式教學；思維；探究

探究式教學是指學生積極參與課堂教學活動，主動探究教學內容，發展創新意識與實踐能力的一種教學方式.這種教學方式更注重“探究”過程，學生通過獨立思考或合作探究完成學習任務，這是一種化被動為主動的學習模式，學生在思維、情感等方面都體現出“主動性”[1].

1 教學過程

1.1 舊知回顧，思維熱身

師：請大家回顧一次函數、反比例函數的定義與一般形式，說說它們和整式之間是否存在什么聯系.當初學習一次函數的基本流程是什么？

生1：一次函數的解析式中y=kx+b（k≠0）等號右邊為關于x的一次整式，即一次二項式或一次單項式.

師：著重強調“k≠0”這個條件的理由是什么？

生2：當k=0時，函數y=kx+b就是y=b（非一次函數）的情況，此為常函數.

設計意圖：在舊知回顧的基礎上創設學生感興趣的情境，能有效激發學生的探究欲，達到讓學生的思維熱身的作用，為進一步進入探索狀態、構建新的概念奠定基礎.

1.2 創設情境，引發探究

探究1生活中常見這樣一種現象：將一顆石子扔進水里，水面會呈現出不斷向外擴展的波紋，這些波紋構成一系列同心圓，分別說說此過程中的常量與變量，變量間存在怎樣的聯系等.

生3：波紋所形成的圓的周長C和圓的半徑R之間的關系為C=2πR.

師：周長是否為半徑的一次函數？判斷依據是什么？

生4：結合函數及一次函數的定義可確定周長是半徑的一次函數.

師：還有其他發現嗎？

學生分別提出：①水波紋形成的圓的面積S和圓的半徑R間的關系為S=πR²；②石子掉入水中的深度h與掉落時間t之間的關系為h=1/2at²；③石子掉入水中所形成的聲音會隨著時間的延長而變小，但無法用函數關系式表達，應該也是一種函數關系.

探究2若張伯準備用16 m長的籬笆筑成一個長方形的家禽飼養場，其中有哪些是變量，哪些是常量，各個量之間存在怎樣的聯系？你是如何判斷的？

生5：該情境中，籬笆的長度16 m固定不變，是常量，而長方形的長與寬（x與y）是變量，同時長方形的面積S也為變量，其中存在的關系為x+y=8，y=8－x（0＜x＜8），S=x（8－x）（0＜x＜8）.

變式1張伯準備用16 m長的籬笆圍成一個家禽飼養場，其中有一面靠墻（墻壁足夠長），若圍成的長方形中與墻面垂直的邊長是x m，請寫出飼養場面積S和x之間的關系式.

結論：S=x（16－2x）=－2x²+16x（0＜x＜8）.

變式2用一段16 m長的籬笆靠10 m長的墻圍成一個長方形的家禽飼養場，所圍成飼養場的面積S與長x（單位： m）之間存在怎樣的關系？并判斷是否為函數、一次函數或反比例函數.

結論：S=x（16－2x）=－2x²+16x（3≤x＜8）.

設計意圖：課堂中好的問題不僅能激趣啟思，還能開闊視野，挖掘學生的潛能，讓學生由表及里地理解問題本質，形成思辨能力.

探究3若想為一面長、寬之比為2∶1的鏡子鑲上邊框，已知鏡面價格為120元/m²，邊框價格為30元/m，工費為45元/次.假設鏡面的寬度是x（單位：m），所需花費的總費用y與x間是怎樣的函數關系？

學生自主探究，過程如下：①鏡面需要120×2x²=240x²（元）；②邊框需要30×6x=180x（元）；③總費用y=240x²+180x+45（元）.

類比一次函數的概念，學生將幾個未接觸的函數羅列在一起，通過其中存在的共同點推斷出二次函數的概念.通過以上探究，發現S=πR²，h=1/2at²，y=240x²+180x+45等，都屬于二次函數的范疇.繼續與一次函數的一般形式類比，學生不僅自主寫出二次函數的一般形式y=ax²+bx+c，還確定了a，b，c是常數，且a≠0的條件，其中x，y分別為自變量與因變量，y為x的函數.

師：對于二次函數的定義，還有什么特別值得關注的地方嗎？

生6：a一定不能為0，若為0，那么函數的最高次項就不是二次項了.

師：不錯，現在大家來觀察S==－2x²+16x（0＜x＜8）與S=－2x²+16x（3≤x＜8），它們的表達式完全一樣，能否確定它們為相同的函數？

設計意圖：以情境的方式引導學生對問題進行引申、發散，不僅能夯實學生對函數概念的理解，還為接下來探索二次函數圖象的性質奠定基礎.利用“自變量取值范圍對函數的影響”，進一步提升數學思維能力，培養學生的創新意識.

1.3 練習訓練，辨析概念

（1）如果y=kxk+1為關于x的二次函數，則k的值是多少？

（2）如果y=（k+1）x|k|+1為關于x的二次函數，則k的值是多少？

（3）如果y=kx|k|+1+2x²+3x為關于x的二次函數，則k的值是多少？

設計意圖：練習訓練意在進一步幫助學生夯實對二次函數定義的理解，起到辨析定義的作用.學生的思維隨著問題難度的增加而深入，新知的應用能力也在問題的解決中得以有效提升，這也是發展學生數學思維的過程.

1.4 應用概念，完善認知

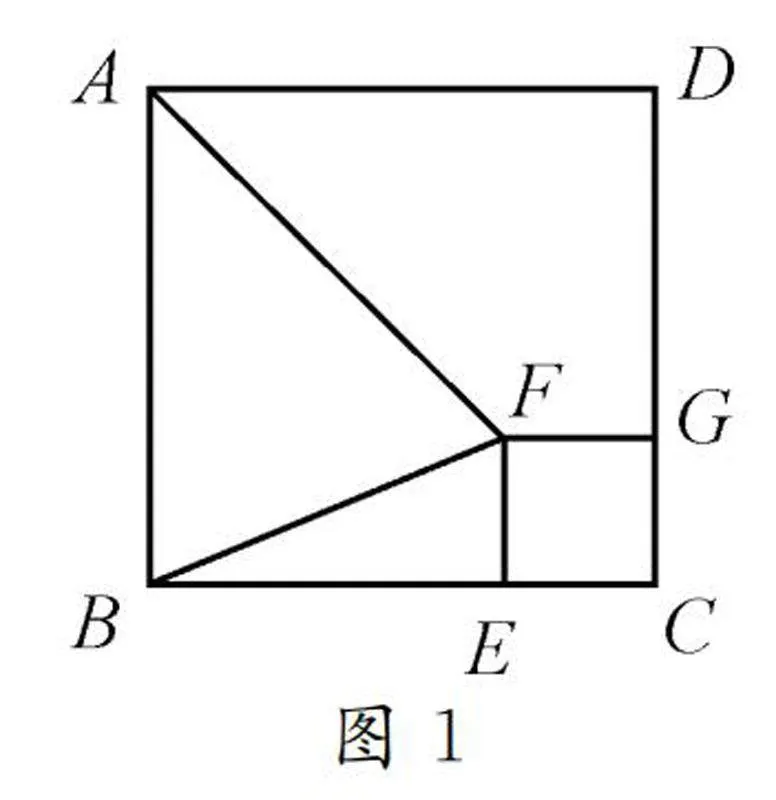
圖1如圖1，已知正方形ABCD的邊長為10，E為BC邊上的一個動點，將EC作為邊長，在正方形ABCD的內部作一個新的正方形EFGC，點G位于邊CD上，分別連接FA，FB，當點E在BC邊上運動時，此時圖中變量間存在怎樣的函數關系？

設計意圖：此例為概念的實際應用問題，意在完善學生的認知結構，讓學生學會靈活應用所學知識來解決實際問題，凸顯合作交流在探究式教學中的重要意義，進一步提升學力.

1.5 課堂總結，拓展延伸

師：回顧本節課的教學，我們探究了哪些內容？分別用什么方法進行探究的？掌握了二次函數的概念之后，接下來還需要掌握與之相關的哪些知識呢？

學生總結回顧本節課的學習歷程、探究過程等，提出二次函數等號右側為二次整式，且當y=0時，其一般形式就變成了ax²+bx+c=0，此為大家熟悉的一元二次方程；當y≥0或y≤0時，y=ax²+bx+c可轉化為ax²+bx+c≥0或ax²+bx+c≤0.

類比一次函數與反比例函數的教學研究套路，接下來應探索二次函數的圖象、性質以及應用等.

2 教學思考

2.1 突出學生主體性

新課標強調學生是課堂的主人，探究式學習以學生的自主探究與合作學習為主，整個教學過程都需將學生放在主體地位.本節課中，不論是對情境的探究，還是知識的應用，抑或最終的總結，都在“以生為本”的基礎上實施.這不僅體現了學生的主人翁意識，還從真正意義上起到育人的作用，為促進學生的終身可持續性發展奠定基礎.

2.2 創設合理的探究情境

對于初中階段的學生而言，他們的數學觀、價值觀已經初步建立，對事物也具有一定的獨立思考能力.教師在探究情境的選擇上需結合學生的認知發展規律，創設學生感興趣的情境來調動學生的探索欲，為教學營造良好的氛圍[2].

如本節課的三個探究情境都是基于學生的認知基礎而創設的，每個情境看似平常，卻又能成功激發學生的探索欲，但又不會出現情境大于問題喧賓奪主的情況.在這三個情境的引導下，學生的思維由淺入深一步步進入二次函數定義的探究中，不僅成功揭露了概念的內涵與外延，還為發展解題能力夯實了知識與技能基礎.

2.3 提出高質量的探究問題

數學教學實則是解決問題的過程，隨著一個個問題的突破，知識本質與結構也逐漸暴露在學生面前.因此課堂中的每一個問題都要經過深思熟慮，切忌想到哪兒問到哪兒，而應有節奏、有目的地設計高質量的探究問題，讓學生的思維在問題的驅動下逐漸深入，最終形成完整的知識結構[3].

參考文獻：

[1]郝樂，馬乾凱，郝一凡，等.數學教育與邏輯思維能力的培養[J].數學教育學報，2013（6）：9-11.

[2]鄭毓信.數學教育視角下的“核心素養”[J].數學教育學報，2016，25（3）：1-5.

[3]王志剛.高中數學新授課中“問題導入”的若干探究[J].教學月刊·中學版（教學參考），2018（10）：37-40.